垂径定理说课课件
图片预览











文档简介
课件32张PPT。垂直于弦的直径人教版九年级上册24.1.2教材分析教学流程创设情景问题探究学以致用课堂检测感悟收获说课模块【教材分析】
垂直于弦的直径是在学生学习了轴对称图形、直角三角形、圆的有关概念的基础上进行的。在学习本节之前已通过折纸、对称、平移、旋转推理证明等方式认识了许多图形的性质,积累了一定的空间与图形的经验。
垂径定理是圆的一个重要的性质定理,它对线段的计算、证明线段相等、弧相等等问题提供了十分简便的方法。 【教学目标】
知识技能:
1.理解圆是轴对称图形.
2.明确垂径定理的题设和结论及定理的推理过程.
3.能初步应用垂径定理进行计算和证明
能力目标:
经历圆是轴对称图形、垂径定理的探究过程,发 展合情
推理能力,体会转化、数形结合的思想.
情感态度:
1、通过对赵州桥历史的了解,渗透爱国教育,感受数学在 生活中的运用,激发学习热情.
2.在探究活动中,学会与人合作,并能与他人交流思维的过 程和探究的结果.
【重难点】
重点:垂径定理及应用.
难点:垂径定理的证明及应用.
【教法学法】
在教学中,充分利用及自制教具进行教学。强调学生的动手操作和主动参与,让他们在大胆猜想、动手操作、观察发现、自主探究、合作交流、归纳总结等大量数学活动中积累有关图形的特征。使学生在学习中体会到:数学活动充满着探索和创造,以提高学习数学的兴趣,培养学生敢于面对数学活动中的困难并有独立克服困难和运用知识解决问题的成功体验。体现新课程精神,把学习的主动权放手给学生。教师起演示、引导作用。 赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦长)是37.4m,拱高(弧的中点到弦的距离)为7.2m,
你能求出赵州桥主桥拱的半径吗? 设计意图
通过对赵州桥历史的了解,渗透爱国教育,让学生感受1300多年前数学在生活中的运用,激发学生学习热情,思考如何解决实际问题.带着问题探究学习。 用纸剪一个圆(课前布置学生准备好)
沿着圆的任意一条直径对折,重复
做几次,你发现了什么?
由此你能得到什么结论? 圆是轴对称图形 ,任何一条直径所在直线都是它的对称轴 设计意图
通过动手折叠,培养学生的动手操作能力,使学生在解决问题的过程中不断探究、学习新知识.
在纸上的圆中任意画一条弦AB 作直径CD垂直弦AB于E(垂直于弦的直径) 垂足为E.想一想:
(1)此图是轴对称图形吗?如果是对称轴是什么?
(2)你能发现哪些相等的线段和弧?为什么?
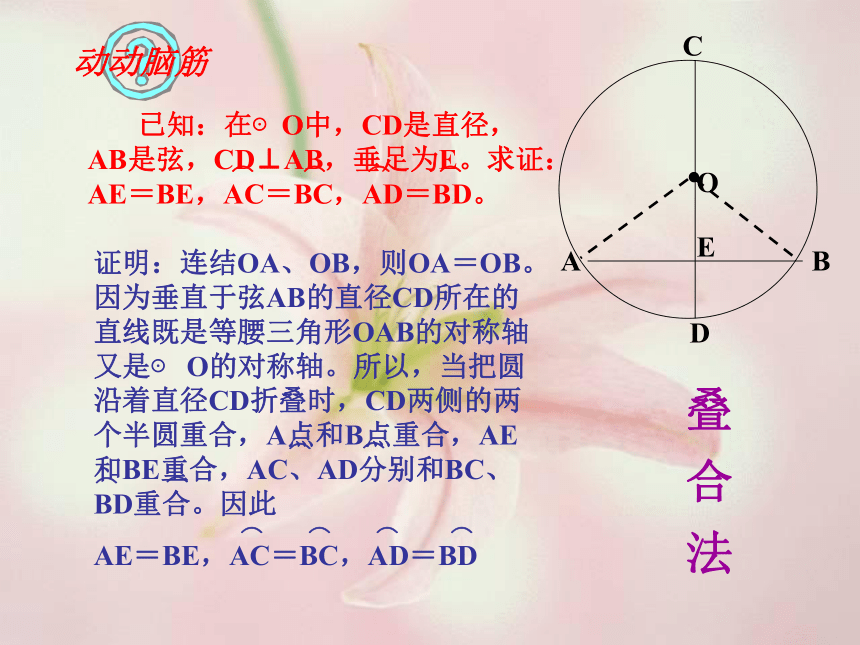
你能得到什么结论?动动脑筋叠 合 法 设计意图
让学生经历知识的形成过程,并围绕问题情景探究思考.使学生明白轴对称图形的性质在证明题时的应用.体验用“叠合”法推证问题的过程,形成解决问题的一些基本策略,发展实践能力和创新精神. 多媒体演示进一步帮助理解,规范学生证明步骤。 垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。题设结论(1)过圆心
(2)垂直于弦}{(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧想一想:下列图形是否可以使用垂径定理?为什么? 问题:把垂径定理中的题设垂直于弦的
直径换为平分弦的直径。你会得到什么结论?
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。 设计意图
分析垂径定理的题设和结论帮助学生理解。借助于图形形象直观的加深理解,并为下一步垂径定理的操作、运用打下基础。
做一做
利用垂径定理
(1)你能平分一条弧吗?
学以(2)算一算
现在你能解决求赵州桥主桥拱半径的问题吗?
变式训练
改变赵州桥问题中的条件
(1)已知跨度、半径求拱高。
(2)已知半径、拱高求跨度
(3)已知弦心距、半径求跨度 设计意图
融合课本88页练习第2题、95页习题第8题 .揭示弦、弦心距、半径、拱高四者之间的关系。引导学生把圆的问题转化为直角三角形的问题来解决。 判断(1)垂直于弦的直线平分弦,并且平分弦所对的弧…………………………………………..( )(2)弦所对的两弧中点的连线,垂直于弦,并且经过圆心……………………………………..( )(3)圆的不与直径垂直的弦必不被这条直径平分…………………………………………...( )(4)平分弦的直径垂直于弦,并且平分弦所对的两条弧………………………………………( )×××√1、 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
求证:AC=BD。证明:过O作OE⊥AB,垂足为E,则AE=BE,CE=DE。
AE-CE=BE-DE。
所以,AC=BDE巩固提高 当堂检测
如图,已知在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径 E小结: 解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。 设计意图
设计判断题是为了消除对垂径定理的认识误区;巩固提高和课堂检测目的是进一步巩固定理,利用定理进行计算、证明。使学生明确解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。2、本节课主要运用什么方法来解决一些简单的实际问题?1、经过本节课的学习,你有哪些收获?小 结感悟与收获 经过本节课的学习,
你有哪些收获?
请和我们一起分享. 感悟收获
1.垂径定理及其应用
2.将垂径定理和勾股定理有机结合,化圆中问题为三角形问题,
3.圆中经常作的辅助线——半径、作弦的垂线
布置作业
已知:在半径为5cm的
⊙O中,两条平行弦AB,CD 分别长8cm、6cm.
求:两条平行弦间的距离谢谢大家谢谢大家
垂直于弦的直径是在学生学习了轴对称图形、直角三角形、圆的有关概念的基础上进行的。在学习本节之前已通过折纸、对称、平移、旋转推理证明等方式认识了许多图形的性质,积累了一定的空间与图形的经验。
垂径定理是圆的一个重要的性质定理,它对线段的计算、证明线段相等、弧相等等问题提供了十分简便的方法。 【教学目标】
知识技能:
1.理解圆是轴对称图形.
2.明确垂径定理的题设和结论及定理的推理过程.
3.能初步应用垂径定理进行计算和证明
能力目标:
经历圆是轴对称图形、垂径定理的探究过程,发 展合情
推理能力,体会转化、数形结合的思想.
情感态度:
1、通过对赵州桥历史的了解,渗透爱国教育,感受数学在 生活中的运用,激发学习热情.
2.在探究活动中,学会与人合作,并能与他人交流思维的过 程和探究的结果.
【重难点】
重点:垂径定理及应用.
难点:垂径定理的证明及应用.
【教法学法】
在教学中,充分利用及自制教具进行教学。强调学生的动手操作和主动参与,让他们在大胆猜想、动手操作、观察发现、自主探究、合作交流、归纳总结等大量数学活动中积累有关图形的特征。使学生在学习中体会到:数学活动充满着探索和创造,以提高学习数学的兴趣,培养学生敢于面对数学活动中的困难并有独立克服困难和运用知识解决问题的成功体验。体现新课程精神,把学习的主动权放手给学生。教师起演示、引导作用。 赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦长)是37.4m,拱高(弧的中点到弦的距离)为7.2m,
你能求出赵州桥主桥拱的半径吗? 设计意图
通过对赵州桥历史的了解,渗透爱国教育,让学生感受1300多年前数学在生活中的运用,激发学生学习热情,思考如何解决实际问题.带着问题探究学习。 用纸剪一个圆(课前布置学生准备好)
沿着圆的任意一条直径对折,重复
做几次,你发现了什么?
由此你能得到什么结论? 圆是轴对称图形 ,任何一条直径所在直线都是它的对称轴 设计意图
通过动手折叠,培养学生的动手操作能力,使学生在解决问题的过程中不断探究、学习新知识.
在纸上的圆中任意画一条弦AB 作直径CD垂直弦AB于E(垂直于弦的直径) 垂足为E.想一想:
(1)此图是轴对称图形吗?如果是对称轴是什么?
(2)你能发现哪些相等的线段和弧?为什么?
你能得到什么结论?动动脑筋叠 合 法 设计意图
让学生经历知识的形成过程,并围绕问题情景探究思考.使学生明白轴对称图形的性质在证明题时的应用.体验用“叠合”法推证问题的过程,形成解决问题的一些基本策略,发展实践能力和创新精神. 多媒体演示进一步帮助理解,规范学生证明步骤。 垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。题设结论(1)过圆心
(2)垂直于弦}{(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧想一想:下列图形是否可以使用垂径定理?为什么? 问题:把垂径定理中的题设垂直于弦的
直径换为平分弦的直径。你会得到什么结论?
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。 设计意图
分析垂径定理的题设和结论帮助学生理解。借助于图形形象直观的加深理解,并为下一步垂径定理的操作、运用打下基础。
做一做
利用垂径定理
(1)你能平分一条弧吗?
学以(2)算一算
现在你能解决求赵州桥主桥拱半径的问题吗?
变式训练
改变赵州桥问题中的条件
(1)已知跨度、半径求拱高。
(2)已知半径、拱高求跨度
(3)已知弦心距、半径求跨度 设计意图
融合课本88页练习第2题、95页习题第8题 .揭示弦、弦心距、半径、拱高四者之间的关系。引导学生把圆的问题转化为直角三角形的问题来解决。 判断(1)垂直于弦的直线平分弦,并且平分弦所对的弧…………………………………………..( )(2)弦所对的两弧中点的连线,垂直于弦,并且经过圆心……………………………………..( )(3)圆的不与直径垂直的弦必不被这条直径平分…………………………………………...( )(4)平分弦的直径垂直于弦,并且平分弦所对的两条弧………………………………………( )×××√1、 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
求证:AC=BD。证明:过O作OE⊥AB,垂足为E,则AE=BE,CE=DE。
AE-CE=BE-DE。
所以,AC=BDE巩固提高 当堂检测
如图,已知在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径 E小结: 解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。 设计意图
设计判断题是为了消除对垂径定理的认识误区;巩固提高和课堂检测目的是进一步巩固定理,利用定理进行计算、证明。使学生明确解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。2、本节课主要运用什么方法来解决一些简单的实际问题?1、经过本节课的学习,你有哪些收获?小 结感悟与收获 经过本节课的学习,
你有哪些收获?
请和我们一起分享. 感悟收获
1.垂径定理及其应用
2.将垂径定理和勾股定理有机结合,化圆中问题为三角形问题,
3.圆中经常作的辅助线——半径、作弦的垂线
布置作业
已知:在半径为5cm的
⊙O中,两条平行弦AB,CD 分别长8cm、6cm.
求:两条平行弦间的距离谢谢大家谢谢大家
同课章节目录
