点和圆的位置关系说课课件
文档属性
| 名称 | 点和圆的位置关系说课课件 |  | |
| 格式 | zip | ||
| 文件大小 | 781.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-18 21:11:55 | ||
图片预览






文档简介
课件20张PPT。过三点的圆初 中 数 学人教版九年级(上)
24.2.1点与圆 的位置关系教材分析: 本节课是在学习了圆的基本概念和性质、圆周角和圆心角之后讲到的。它是圆的基本知识,是确定圆的理论依据,也是解决实际问题的常用方法。它既能和前面所学知识进行联系,又为以后学习点与圆、直线与圆以及圆与圆的位置关系提供理论依据,为三角形的内切圆的画法提供策略,所以,本节课起着重要的作用。 教学目标:知识与技能:通过作图,探索不在同一直线上三点确定一 个圆的结论,并能运用它解决实际问题,掌握三角形外接圆、外心等概念,会求特殊三角形外接圆的半径。
过程与方法:通过不在同一直线上三点确定一个圆的过程,渗透类比思想、分类讨论思想,培养学生的探究能力和归纳能力,学会解决问题的策略和方法,提高作图能力。
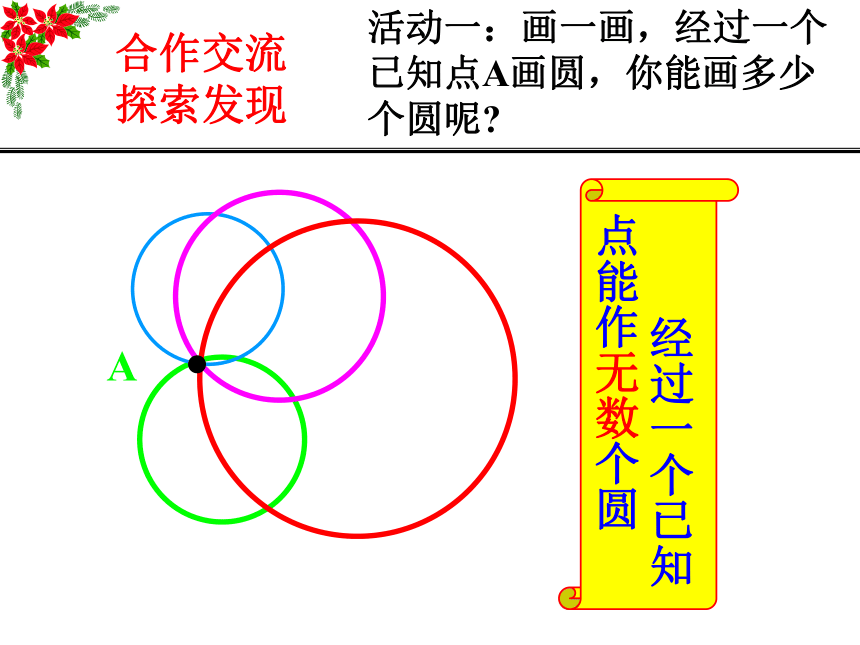
情感态度、价值观:让学生学会与他人合作交流,在探究的过程中感受成功,建立自信;通过作图,养成做事认真,精益求精的良好心里品质及动手操作能力。教学重点: 不在同一直线上三点确定一个圆的结论和作图方法以及获得这些知识的探究过程。教学难点: 能熟练准确的过不在同一直线上的三点作圆。 已知: A、B、C三个村庄位置如图,现要修建一个水塔, 使三个村到水塔的距离相等。请画出水塔的位置.请同学们来解决一个问题:知识回顾教学流程某居民小区的一片空地上有三颗古树,现准备在这片空地上建一个圆形广场,为使古树不被破坏,设计时要求古树恰好在圆形广场的边缘上,要怎样画出设计图呢?想一想 确定一个圆的关键条件是什么?创设情境引入新课活动一:画一画,经过一个已知点A画圆,你能画多少个圆呢? 经过一个已知点能作无数个圆
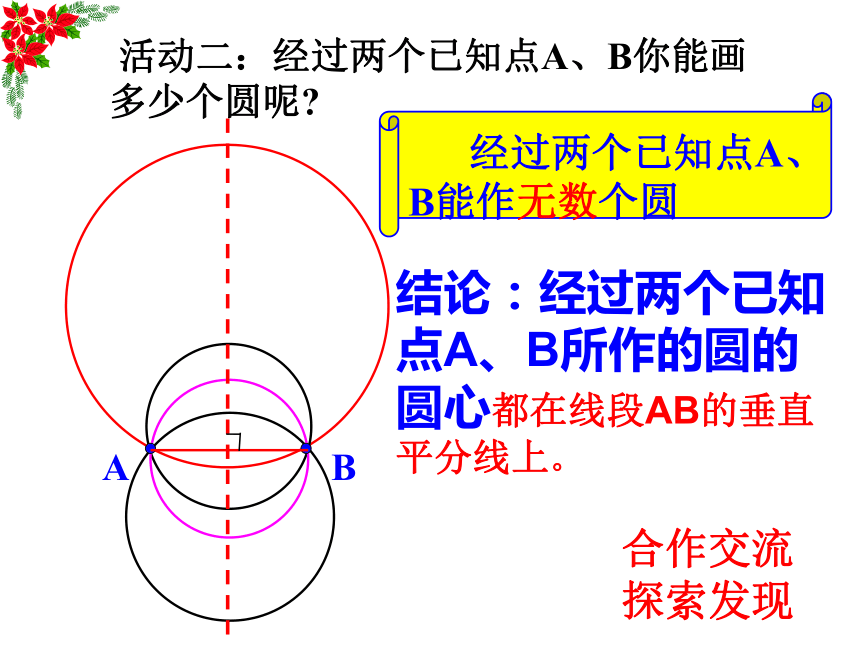
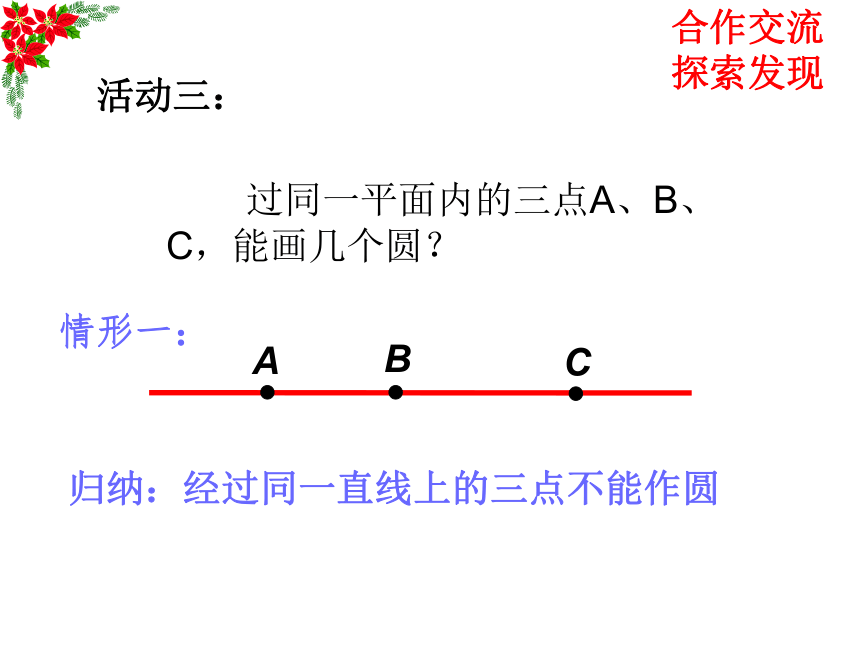
合作交流探索发现A 活动二:经过两个已知点A、B你能画多少个圆呢?AB 经过两个已知点A、B能作无数个圆结论:经过两个已知点A、B所作的圆的圆心都在线段AB的垂直平分线上。合作交流探索发现 过同一平面内的三点A、B、C,能画几个圆?活动三:归纳:经过同一直线上的三点不能作圆合作交流探索发现情形一:例题:已知:不在同一直线上的三点A、B、C,
求作:⊙O,使它经过点A、B、C。做法:1、连接AB,作线段AB的垂直平分线DE。2、连接BC,作线段BC的垂直平分线FG,交DE于点O。3、以O为圆心,以OB为半径作圆。ABCEG⊙O就是所求作的圆合作交流探索发现情形二:三点不共线时FD自主学习 理解概念自学教材92页,掌握三角形外接圆、外心的概念归纳:经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形。如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等。你能画出过以下三角形的外接圆吗?(小组合作完成)●OCAB┐●O●O思 考说一说:比较这三个三角形外心的位置,你有何发现?
证一证:你能验证图二的结论是对的吗?(图一)(图二)(图三)应用新知探索规律总结归纳:
1.三角形的外心是三角形三边垂直平分线的交点。
2.三角形的外心到三角形三个顶点的距离相等。
3.锐角三角形的外心在三角形的内部。
直角三角形的外心是三角形的斜边中点。
钝角三角形的外心在三角形的外部。
反之成立。应用新知探索规律ABC学生叙述做法学以致用回应前文如何解决“破镜重圆”的问题:解决问题的关键是什么?(找圆心)学以致用联系实际
随意画出四点,其中任何三点都不在同一条直线上,是否一定可以画一个圆呢?如果能它们应满足什么条件。请同学们讨论!ABCD拓展延伸应用迁移1、数学知识技能2、数学思想方法3、数学情感价值梳理知识回顾反思一.判断题:
1.过三点一定可以作圆 ( )
2.三角形有且只有一个外接圆 ( )
3.任意一个圆有一个内接三角形,并且只有
一个内接三角形 ( )
4.三角形的外心就是这个三角形任意两边垂
直平分线的交点 ( )
5.三角形的外心到三边的距离相等 ( )达标检测学情反馈达标检测学情反馈四.如图所示,在四边形ABCD中,∠B=∠D=90。试证明四边形ABCD有外接圆。三. 已知△ABC中,AB=5,BC=13,AC=12,求△ABC的外接圆的面积。如图所示,△ ABC是圆O的_____三角形;圆O是
△ ABC的_____。
2. 在Rt△ABC中,∠C=90°,AB=5cm,则其外接圆的半径为____________。
3. 已知正△ABC的边长为6cm,则其外接圆的半径为 _______ cm。
若正三角形的边长为a,则其外接圆的半径为______(用a来表示)二. 填空题作业设计巩固提高分层作业:1.必做题:教材93页练习题第3题
102页习题24.2第8题和第10题2.选做题:教材93页第四题
24.2.1点与圆 的位置关系教材分析: 本节课是在学习了圆的基本概念和性质、圆周角和圆心角之后讲到的。它是圆的基本知识,是确定圆的理论依据,也是解决实际问题的常用方法。它既能和前面所学知识进行联系,又为以后学习点与圆、直线与圆以及圆与圆的位置关系提供理论依据,为三角形的内切圆的画法提供策略,所以,本节课起着重要的作用。 教学目标:知识与技能:通过作图,探索不在同一直线上三点确定一 个圆的结论,并能运用它解决实际问题,掌握三角形外接圆、外心等概念,会求特殊三角形外接圆的半径。
过程与方法:通过不在同一直线上三点确定一个圆的过程,渗透类比思想、分类讨论思想,培养学生的探究能力和归纳能力,学会解决问题的策略和方法,提高作图能力。
情感态度、价值观:让学生学会与他人合作交流,在探究的过程中感受成功,建立自信;通过作图,养成做事认真,精益求精的良好心里品质及动手操作能力。教学重点: 不在同一直线上三点确定一个圆的结论和作图方法以及获得这些知识的探究过程。教学难点: 能熟练准确的过不在同一直线上的三点作圆。 已知: A、B、C三个村庄位置如图,现要修建一个水塔, 使三个村到水塔的距离相等。请画出水塔的位置.请同学们来解决一个问题:知识回顾教学流程某居民小区的一片空地上有三颗古树,现准备在这片空地上建一个圆形广场,为使古树不被破坏,设计时要求古树恰好在圆形广场的边缘上,要怎样画出设计图呢?想一想 确定一个圆的关键条件是什么?创设情境引入新课活动一:画一画,经过一个已知点A画圆,你能画多少个圆呢? 经过一个已知点能作无数个圆
合作交流探索发现A 活动二:经过两个已知点A、B你能画多少个圆呢?AB 经过两个已知点A、B能作无数个圆结论:经过两个已知点A、B所作的圆的圆心都在线段AB的垂直平分线上。合作交流探索发现 过同一平面内的三点A、B、C,能画几个圆?活动三:归纳:经过同一直线上的三点不能作圆合作交流探索发现情形一:例题:已知:不在同一直线上的三点A、B、C,
求作:⊙O,使它经过点A、B、C。做法:1、连接AB,作线段AB的垂直平分线DE。2、连接BC,作线段BC的垂直平分线FG,交DE于点O。3、以O为圆心,以OB为半径作圆。ABCEG⊙O就是所求作的圆合作交流探索发现情形二:三点不共线时FD自主学习 理解概念自学教材92页,掌握三角形外接圆、外心的概念归纳:经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形。如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等。你能画出过以下三角形的外接圆吗?(小组合作完成)●OCAB┐●O●O思 考说一说:比较这三个三角形外心的位置,你有何发现?
证一证:你能验证图二的结论是对的吗?(图一)(图二)(图三)应用新知探索规律总结归纳:
1.三角形的外心是三角形三边垂直平分线的交点。
2.三角形的外心到三角形三个顶点的距离相等。
3.锐角三角形的外心在三角形的内部。
直角三角形的外心是三角形的斜边中点。
钝角三角形的外心在三角形的外部。
反之成立。应用新知探索规律ABC学生叙述做法学以致用回应前文如何解决“破镜重圆”的问题:解决问题的关键是什么?(找圆心)学以致用联系实际
随意画出四点,其中任何三点都不在同一条直线上,是否一定可以画一个圆呢?如果能它们应满足什么条件。请同学们讨论!ABCD拓展延伸应用迁移1、数学知识技能2、数学思想方法3、数学情感价值梳理知识回顾反思一.判断题:
1.过三点一定可以作圆 ( )
2.三角形有且只有一个外接圆 ( )
3.任意一个圆有一个内接三角形,并且只有
一个内接三角形 ( )
4.三角形的外心就是这个三角形任意两边垂
直平分线的交点 ( )
5.三角形的外心到三边的距离相等 ( )达标检测学情反馈达标检测学情反馈四.如图所示,在四边形ABCD中,∠B=∠D=90。试证明四边形ABCD有外接圆。三. 已知△ABC中,AB=5,BC=13,AC=12,求△ABC的外接圆的面积。如图所示,△ ABC是圆O的_____三角形;圆O是
△ ABC的_____。
2. 在Rt△ABC中,∠C=90°,AB=5cm,则其外接圆的半径为____________。
3. 已知正△ABC的边长为6cm,则其外接圆的半径为 _______ cm。
若正三角形的边长为a,则其外接圆的半径为______(用a来表示)二. 填空题作业设计巩固提高分层作业:1.必做题:教材93页练习题第3题
102页习题24.2第8题和第10题2.选做题:教材93页第四题
同课章节目录
