垂直平分线说课稿
图片预览






文档简介
课件26张PPT。线段的垂直平分线《线段的垂直平分线》说课设计线段的垂直平分线教学理念教学内容教学目标教学策略教学过程教学理念 《数学课程标准》指出:“数学教学应当从学生实际出发,创设有助于学生自主学习的问题情境,引导学生通过实践、思考、探索、交流,获得知识,形成技能,发展思维,学会学习,促使学生在教师指导下生动活泼地、主动地、富有个性地学习。”数学教学是数学活动的教学,是师生之间,学生之间交流互动与共同发展的过程,数学教学要实现知识、能力、情感三维目标的统一协调发展。教学内容 本节课是八年级上学期第12章第一节轴对称中第二课时内容,它即是对前一课时关于轴对称图形性质的再认识,又是今后几何作图、证明、计算的基础。学习过程中渗透的转化、探索、归纳等数学思想方法对学生今后的数学学习也有重要的意义。学习线段垂直平分线相关知识是为学生创造了一次探究的机会,是学习几何学的一次磨练,更是学生学习几何学的一次成长经历。
本节课的教学重点是线段垂直平分线的性质;难点是线段垂直平分线性质的理解和准确运用。教学目标知识与技能目标:证明、理解线段垂直平分线的性质,并会准确 运用性质解决有关问题
过程与方法目标:经历线段垂直平分线性质的探究过程,通过观 察,猜想,探究,论证,归纳获得知识,体会 转化、探究、归纳等数学思想,发展推理能力 ,体验合作学习
情感与态度目标:通过对线段垂直平分线性质的探究,激发学生 的好奇心和求知欲,并在运用数学知识解答问 题的活动中获得成功的体验,建立学习的自信 心教学策略 教学活动必须建立在学生的认知发展水平和已有的知识经验基础之上;在学习活动中不能单纯的依赖模仿与记忆,动手实践、自主探索与合作交流是学生学习数学的主要方式;适当的竞争机制和评价体系又可以有效的激发学生的潜力。所以本节课我将借助多媒体辅助教学,配备简单的教具,注重营造轻松的学习氛围,创设学生熟悉并且有兴趣的情景,学生将以小组为学习单位,合作交流,借助适当的竞争机制和评价体系激励小组间展开竞争, 丰富学习成果。
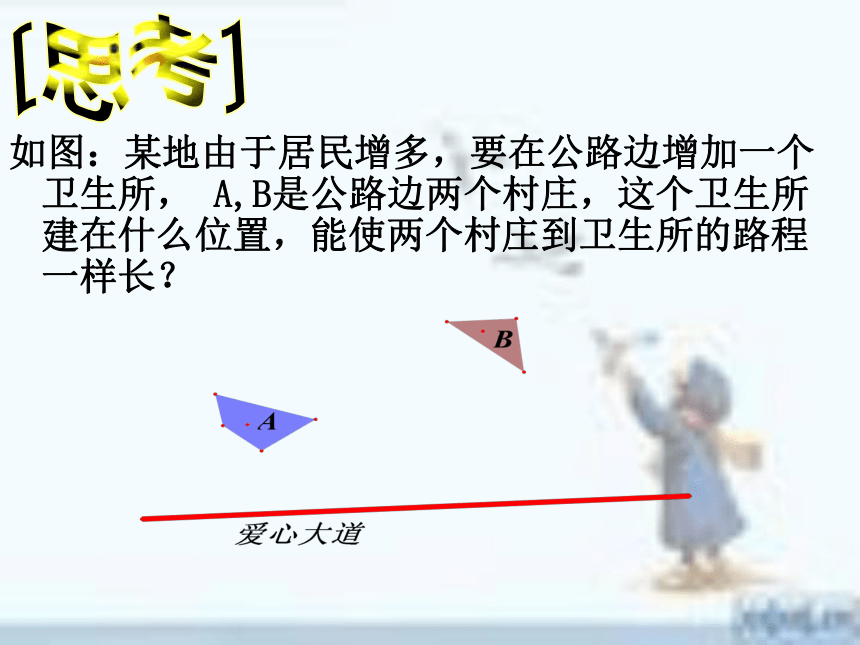
我认为再警惕的野兽看到诱食也会动心,抓住学生的好奇心,好胜心是本节课我的主要工作方向,争作课堂上的猎人是我本节课的角色定位,学生是课堂上的野兽,如何满足他们的欲望是我的工作目标,把野兽最终培养成野兽中的猎人是我的最终目的。 教学流程图性质1性质2知识运用作图方法问题情景小结结束开始分析比较作业[思考]如图:某地由于居民增多,要在公路边增加一个卫生所, A,B是公路边两个村庄,这个卫生所建在什么位置,能使两个村庄到卫生所的路程一样长?十七般兵器十七般兵器以左图弓箭图形为例,弓的形状和我们学习的那种几何图形比较相似?它是 轴堆成图形码?如果是,请你大概描述出对称轴的位置,并且在弓身找出几组对称的点?图形中的红线(对称点的连线段)和黄线(对称轴)是怎样的位置关系? AABBCC开弓时图形仍然是轴对称的吗?此时图形和我们学习过什么几何图形比较相似呢?利用轴对称相关知识你发现那些线段相等呢?
此时的箭和弓是什么位置关系呢?ABCO如图,木条l与AB钉在一起,l垂直平分AB,点P是l上的点,当点P在l上移动时,分别量出点P到A、B的距离, 你有什么发现?你能证明你的结论吗?2.根据条件OA=OB、∠AOP=∠BOP、OP=OP ,由SAS可以得出
△AOP≌△BOP,
于是得出
AP=BP .实验设计1.利用直尺测量AP和BP 的长度线段垂直平分线上的点到线段两端点距离相等 即: ∵ PR垂直平分线段AB ∴ A P=B P A Q=B Q A R=B R性质1:如图:直线PR垂直平分线段AB
求证: AP=BP ( AQ=BQ AR=BR)
证明:∵直线PR垂直平分线段AB
∴AO=BO, ∠AOP= ∠BOP=90°
∵OP=OP
∴△AOP≌ △BOP(SAS)
∴ AP=BP
同理可得AQ=BQ AR=BR
运动员射出的箭又平又直能够轻松射中靶心,你知道其中的秘密吗,仔细观察他们射箭时的动作,你有什么发现吗?你现在是不是也想试一试呢?如图:用一跟木棒和一根弹性均匀的橡皮筋,做一个简易的“弓”,“箭”通过木棒中央的孔射出去,怎样才能保持射出箭的方向与木帮垂直呢?为什么?ABCO实验设计1.当AC=BC时,测量∠AOC2.根据 AO=BO,AC=BC,OC=OC
由SSS可以得出
△AOC≌△BOC
于是得出∠AOC=90°性质2:到一条线段两个端点距离相等的点在这条线段的垂直平分线上
即:∵AP=BP
∴点P在AB的垂直平分线上
思考:比较性质1和性质2,你发现它们是什么关系了呢? 小组内完成性质2的证明如图:BD垂直平分CE,ED=3㎝, △ABE的周长为11 ㎝,则△ABC的周长为____练一练如图:AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB,AC,CE的长度有什么关系?AB+BD与DE有什么关系?练一练如图:AB=AC,MB=MC,直线 AM 是线段BC的垂直平分线吗?想一想我们如何去作一条线段的垂直平分线呢,通过本题你得到了什么启示了吗?练一练作线段AB的垂直平分线知识点3:CD1.分别以点A,B为圆心,以大于1/2AB的长为半径作弧,两弧相交与 C,D两点
2.作直线 CD
CD 既为所求的直线如图:某地由于居民增多,要在公路边增加一个卫生所, A,B是公路边两个村庄,这个卫生所建在什么位置,能使两个村庄到卫生所的路程一样长?P你能行1.通过本节课你收获了那些知识?
2.你是不是又想到了一些有趣的课题去探究?
小结作业1.在△ABC中,边AB、BC的垂直平分线交于点P。求证(1) PA=PB=PC. (2) 点P在AC的垂直平分线上 2.电信部门要修建一座电视信号发射塔,如图所示,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条高速公路m和n的距离也必须相等,请你确定发射塔应修建在什么位置?在图上标出它的位置。 板 书 设 计线段垂直平分线上的点到线段两端点距离相等 即: ∵ PR垂直平分线段AB ∴ AP=BP AQ=BQ AR=BR到一条线段两个端点距离相等的点在这条线段的垂直平分线上
即:∵AP=BP
∴点P在AB的垂直平分线上尺规作图
1.分别以点A,B为圆心,以大于1/2AB的长为半径作弧,两弧相交与 C,D两点
2.作直线 CD
CD 既为所求的直线
线段的垂直平分线作业DC反思1.本节课创设了学生较感兴趣的问题情景
2.知识的形成过程符合对事物的一般认知规律
3.学生自主探究、合作交流,学生学习的内因较强
4.习题设置较为得当,促使学生形成知识技能,
提高数学涵养,明确了学习数学的目的
请批评指正谢谢!
本节课的教学重点是线段垂直平分线的性质;难点是线段垂直平分线性质的理解和准确运用。教学目标知识与技能目标:证明、理解线段垂直平分线的性质,并会准确 运用性质解决有关问题
过程与方法目标:经历线段垂直平分线性质的探究过程,通过观 察,猜想,探究,论证,归纳获得知识,体会 转化、探究、归纳等数学思想,发展推理能力 ,体验合作学习
情感与态度目标:通过对线段垂直平分线性质的探究,激发学生 的好奇心和求知欲,并在运用数学知识解答问 题的活动中获得成功的体验,建立学习的自信 心教学策略 教学活动必须建立在学生的认知发展水平和已有的知识经验基础之上;在学习活动中不能单纯的依赖模仿与记忆,动手实践、自主探索与合作交流是学生学习数学的主要方式;适当的竞争机制和评价体系又可以有效的激发学生的潜力。所以本节课我将借助多媒体辅助教学,配备简单的教具,注重营造轻松的学习氛围,创设学生熟悉并且有兴趣的情景,学生将以小组为学习单位,合作交流,借助适当的竞争机制和评价体系激励小组间展开竞争, 丰富学习成果。
我认为再警惕的野兽看到诱食也会动心,抓住学生的好奇心,好胜心是本节课我的主要工作方向,争作课堂上的猎人是我本节课的角色定位,学生是课堂上的野兽,如何满足他们的欲望是我的工作目标,把野兽最终培养成野兽中的猎人是我的最终目的。 教学流程图性质1性质2知识运用作图方法问题情景小结结束开始分析比较作业[思考]如图:某地由于居民增多,要在公路边增加一个卫生所, A,B是公路边两个村庄,这个卫生所建在什么位置,能使两个村庄到卫生所的路程一样长?十七般兵器十七般兵器以左图弓箭图形为例,弓的形状和我们学习的那种几何图形比较相似?它是 轴堆成图形码?如果是,请你大概描述出对称轴的位置,并且在弓身找出几组对称的点?图形中的红线(对称点的连线段)和黄线(对称轴)是怎样的位置关系? AABBCC开弓时图形仍然是轴对称的吗?此时图形和我们学习过什么几何图形比较相似呢?利用轴对称相关知识你发现那些线段相等呢?
此时的箭和弓是什么位置关系呢?ABCO如图,木条l与AB钉在一起,l垂直平分AB,点P是l上的点,当点P在l上移动时,分别量出点P到A、B的距离, 你有什么发现?你能证明你的结论吗?2.根据条件OA=OB、∠AOP=∠BOP、OP=OP ,由SAS可以得出
△AOP≌△BOP,
于是得出
AP=BP .实验设计1.利用直尺测量AP和BP 的长度线段垂直平分线上的点到线段两端点距离相等 即: ∵ PR垂直平分线段AB ∴ A P=B P A Q=B Q A R=B R性质1:如图:直线PR垂直平分线段AB
求证: AP=BP ( AQ=BQ AR=BR)
证明:∵直线PR垂直平分线段AB
∴AO=BO, ∠AOP= ∠BOP=90°
∵OP=OP
∴△AOP≌ △BOP(SAS)
∴ AP=BP
同理可得AQ=BQ AR=BR
运动员射出的箭又平又直能够轻松射中靶心,你知道其中的秘密吗,仔细观察他们射箭时的动作,你有什么发现吗?你现在是不是也想试一试呢?如图:用一跟木棒和一根弹性均匀的橡皮筋,做一个简易的“弓”,“箭”通过木棒中央的孔射出去,怎样才能保持射出箭的方向与木帮垂直呢?为什么?ABCO实验设计1.当AC=BC时,测量∠AOC2.根据 AO=BO,AC=BC,OC=OC
由SSS可以得出
△AOC≌△BOC
于是得出∠AOC=90°性质2:到一条线段两个端点距离相等的点在这条线段的垂直平分线上
即:∵AP=BP
∴点P在AB的垂直平分线上
思考:比较性质1和性质2,你发现它们是什么关系了呢? 小组内完成性质2的证明如图:BD垂直平分CE,ED=3㎝, △ABE的周长为11 ㎝,则△ABC的周长为____练一练如图:AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB,AC,CE的长度有什么关系?AB+BD与DE有什么关系?练一练如图:AB=AC,MB=MC,直线 AM 是线段BC的垂直平分线吗?想一想我们如何去作一条线段的垂直平分线呢,通过本题你得到了什么启示了吗?练一练作线段AB的垂直平分线知识点3:CD1.分别以点A,B为圆心,以大于1/2AB的长为半径作弧,两弧相交与 C,D两点
2.作直线 CD
CD 既为所求的直线如图:某地由于居民增多,要在公路边增加一个卫生所, A,B是公路边两个村庄,这个卫生所建在什么位置,能使两个村庄到卫生所的路程一样长?P你能行1.通过本节课你收获了那些知识?
2.你是不是又想到了一些有趣的课题去探究?
小结作业1.在△ABC中,边AB、BC的垂直平分线交于点P。求证(1) PA=PB=PC. (2) 点P在AC的垂直平分线上 2.电信部门要修建一座电视信号发射塔,如图所示,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条高速公路m和n的距离也必须相等,请你确定发射塔应修建在什么位置?在图上标出它的位置。 板 书 设 计线段垂直平分线上的点到线段两端点距离相等 即: ∵ PR垂直平分线段AB ∴ AP=BP AQ=BQ AR=BR到一条线段两个端点距离相等的点在这条线段的垂直平分线上
即:∵AP=BP
∴点P在AB的垂直平分线上尺规作图
1.分别以点A,B为圆心,以大于1/2AB的长为半径作弧,两弧相交与 C,D两点
2.作直线 CD
CD 既为所求的直线
线段的垂直平分线作业DC反思1.本节课创设了学生较感兴趣的问题情景
2.知识的形成过程符合对事物的一般认知规律
3.学生自主探究、合作交流,学生学习的内因较强
4.习题设置较为得当,促使学生形成知识技能,
提高数学涵养,明确了学习数学的目的
请批评指正谢谢!
