湘教版八年级数学下册 4.1.1变量与函数 课件(14张PPT)
文档属性
| 名称 | 湘教版八年级数学下册 4.1.1变量与函数 课件(14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 468.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 17:02:39 | ||
图片预览





文档简介
(共14张PPT)
函数和它的表示法
本课内容
4.1
——4.1.1 变量与函数
情境导入
在前面,我们学习了各种数,比如实数、整数、有理数、无理数等。那么请问“函数”也是数吗?
大千世界 万物皆变
行星在宇宙中的位置随时间而变化;
人体细胞的个数随年龄而变化;
气温随海拔而变化;
汽车行驶里程随行驶时间而变化;
……
这几个问题中都涉及两个量之间的关系,它们是一种什么关系呢?
10
20
动脑筋
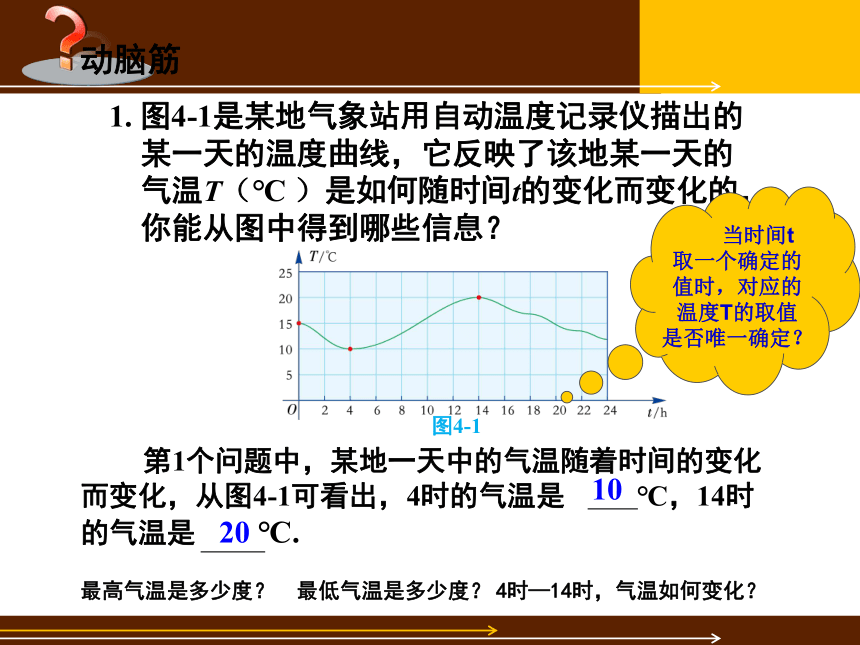
第1个问题中,某地一天中的气温随着时间的变化而变化,从图4-1可看出,4时的气温是 ℃,14时的气温是 ℃.
1. 图4-1是某地气象站用自动温度记录仪描出的
某一天的温度曲线,它反映了该地某一天的
气温T(℃ )是如何随时间t的变化而变化的,
你能从图中得到哪些信息?
图4-1
最高气温是多少度? 最低气温是多少度?
4时—14时,气温如何变化?
当时间t取一个确定的值时,对应的温度T的取值是否唯一确定?
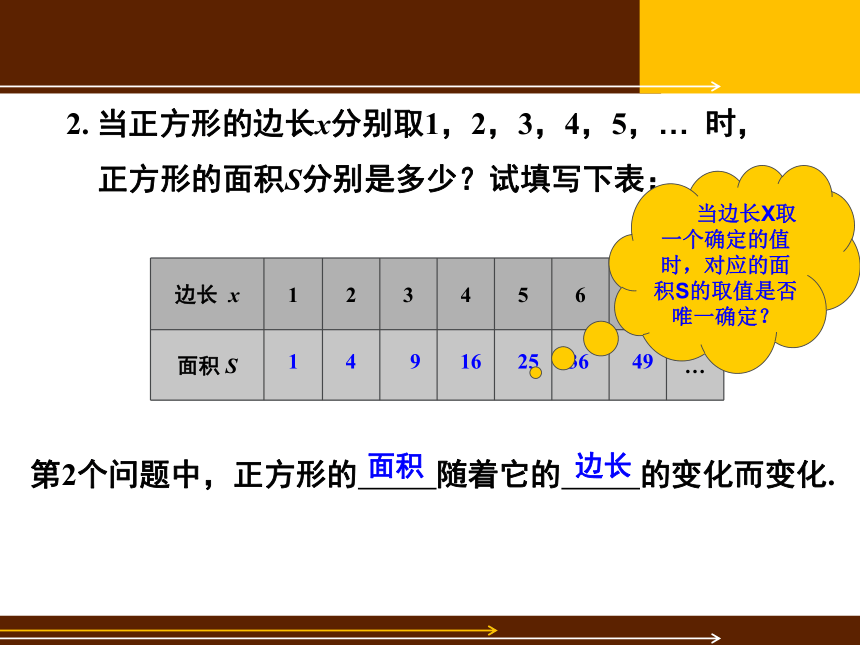
2. 当正方形的边长x分别取1,2,3,4,5,… 时,
正方形的面积S分别是多少?试填写下表:
边长 x 1 2 3 4 5 6 7 …
面积 S …
第2个问题中,正方形的 随着它的 的变化而变化.
1
4
9
16
25
36
49
面积
边长
当边长X取一个确定的值时,对应的面积S的取值是否唯一确定?
某城市居民用的天然气,1 收费2.88元,使用
x( )天然气应缴纳的费用y(元)为y = 2.88x.
当x=10时,缴纳的费用为多少?
3.
第3个问题中,使用天然气缴纳的费用y随所用天然气的体积x的变化而变化. 例如,当x=10时,y=(元);当x=20时,y= (元).
28.8
57.6
当天然气的体积x取一个确定的值时,对应的费用y的取值是否唯一确定?
在讨论的问题中,取值会发生变化的量称为变量,
取值固定不变的量称为常量(或常数).
上述问题中,时间t,气温T;正方形的边长x,面积S;使用天然气的体积x,应交纳的费用y等都是变量. 使用每一方米天然气应交纳2.88元,2.88是常量.
上述三个问题中:
①分别涉及哪些量的关系?
②哪些量是变化的?哪些量是不变的?哪个量的变化导致另一个量的变化而变化?
③在一个问题中,当一个量取了确定的值之后,另一个量对应的能取几个值?
思考
都有两个变量x,y
都是变量y随着x的变化而变化
当x取一个确定值的时候,y只有一个值与之对应.
你能找出它们的共性吗?
一般地,如果变量y随着变量x而变化,并且对于x取的每一个值,y都有唯一的一个值与它对应,那么称y是x的函数,记作y=f(x).
这里的f(x)是英文 a function of x(x的函数)的简记. 这时把x叫作自变量,把y叫作因变量.
对于自变量x取的每一个值a,因变量y的对应值称为函数值,记作f(a).
归纳
函数的概念
指出下列关系式中的变量与常量:
(1) y = 5x -6
(2) y=
(3) y= 4X2+5x-7
(4) S = Лr2
解:(1)5和-6是常量,x和y是变量。
(2)6是常量,x、y是变量。
(3)4、5、-7是常量,x、y是变量。
(4)兀是常量,s、r是变量。
1. 第一个例子中, 是自变量, 是
的函数.
说一说
时间t
气温T
时间t
2. 第二个例子中,正方形的边长是 ,
正方形的面积是边长的 .
自变量
函数
3. 第三个例子中, 是自变量,
是 的函数.
所用天然气的体积x
应交纳费用y
所用天然气的体积x
在考虑两个变量间的函数时,还要注意自变量的取值范围. 如上述第1个问题中,自变量t的取值范围是0≤t≤24;而第2、3个问题中,自变量x的取值范围分别是x>0,x≥0.
注 意
如图4-2,已知圆柱的高是4cm,底面半径是r(cm), 当圆柱的底面半径r由小变大时,圆柱的体积V( )
是r的函数.
(1)用含r 的代数式来表示圆柱的体积V,指出
自变量r 的取值范围.
(2)当r = 5 ,10时,V是多少(结果保留π)?
举
例
例1
图4-2
解
(1) 圆柱的体积 ,自变量r的取值范围
是r > 0.
(2) 当r = 5时, ;
当r = 10 时, .
求下列函数中自变量x的取值范围:
(1) y=3x-1 (2) y=2x2+7
(3) y= (4) y=
(1)因为x取任意实数, 都有意义,所以x的取值范围是任意实数.
(2)因为x取任意实数, 都有意义,所以x的取值范围是任意实数.
(3)因为x+2不等于0时, 才有意义,所以
x的取值范围是:
(4)因为x≥2时, 才有意义,所以x的取值范围是x≥2 .
3、这节课你有什么收获?还有什么疑问?
1、函数是一种“数”吗?
2、在日常生活中,还有哪些量的变化是函数关系?
小 结
函数和它的表示法
本课内容
4.1
——4.1.1 变量与函数
情境导入
在前面,我们学习了各种数,比如实数、整数、有理数、无理数等。那么请问“函数”也是数吗?
大千世界 万物皆变
行星在宇宙中的位置随时间而变化;
人体细胞的个数随年龄而变化;
气温随海拔而变化;
汽车行驶里程随行驶时间而变化;
……
这几个问题中都涉及两个量之间的关系,它们是一种什么关系呢?
10
20
动脑筋
第1个问题中,某地一天中的气温随着时间的变化而变化,从图4-1可看出,4时的气温是 ℃,14时的气温是 ℃.
1. 图4-1是某地气象站用自动温度记录仪描出的
某一天的温度曲线,它反映了该地某一天的
气温T(℃ )是如何随时间t的变化而变化的,
你能从图中得到哪些信息?
图4-1
最高气温是多少度? 最低气温是多少度?
4时—14时,气温如何变化?
当时间t取一个确定的值时,对应的温度T的取值是否唯一确定?
2. 当正方形的边长x分别取1,2,3,4,5,… 时,
正方形的面积S分别是多少?试填写下表:
边长 x 1 2 3 4 5 6 7 …
面积 S …
第2个问题中,正方形的 随着它的 的变化而变化.
1
4
9
16
25
36
49
面积
边长
当边长X取一个确定的值时,对应的面积S的取值是否唯一确定?
某城市居民用的天然气,1 收费2.88元,使用
x( )天然气应缴纳的费用y(元)为y = 2.88x.
当x=10时,缴纳的费用为多少?
3.
第3个问题中,使用天然气缴纳的费用y随所用天然气的体积x的变化而变化. 例如,当x=10时,y=(元);当x=20时,y= (元).
28.8
57.6
当天然气的体积x取一个确定的值时,对应的费用y的取值是否唯一确定?
在讨论的问题中,取值会发生变化的量称为变量,
取值固定不变的量称为常量(或常数).
上述问题中,时间t,气温T;正方形的边长x,面积S;使用天然气的体积x,应交纳的费用y等都是变量. 使用每一方米天然气应交纳2.88元,2.88是常量.
上述三个问题中:
①分别涉及哪些量的关系?
②哪些量是变化的?哪些量是不变的?哪个量的变化导致另一个量的变化而变化?
③在一个问题中,当一个量取了确定的值之后,另一个量对应的能取几个值?
思考
都有两个变量x,y
都是变量y随着x的变化而变化
当x取一个确定值的时候,y只有一个值与之对应.
你能找出它们的共性吗?
一般地,如果变量y随着变量x而变化,并且对于x取的每一个值,y都有唯一的一个值与它对应,那么称y是x的函数,记作y=f(x).
这里的f(x)是英文 a function of x(x的函数)的简记. 这时把x叫作自变量,把y叫作因变量.
对于自变量x取的每一个值a,因变量y的对应值称为函数值,记作f(a).
归纳
函数的概念
指出下列关系式中的变量与常量:
(1) y = 5x -6
(2) y=
(3) y= 4X2+5x-7
(4) S = Лr2
解:(1)5和-6是常量,x和y是变量。
(2)6是常量,x、y是变量。
(3)4、5、-7是常量,x、y是变量。
(4)兀是常量,s、r是变量。
1. 第一个例子中, 是自变量, 是
的函数.
说一说
时间t
气温T
时间t
2. 第二个例子中,正方形的边长是 ,
正方形的面积是边长的 .
自变量
函数
3. 第三个例子中, 是自变量,
是 的函数.
所用天然气的体积x
应交纳费用y
所用天然气的体积x
在考虑两个变量间的函数时,还要注意自变量的取值范围. 如上述第1个问题中,自变量t的取值范围是0≤t≤24;而第2、3个问题中,自变量x的取值范围分别是x>0,x≥0.
注 意
如图4-2,已知圆柱的高是4cm,底面半径是r(cm), 当圆柱的底面半径r由小变大时,圆柱的体积V( )
是r的函数.
(1)用含r 的代数式来表示圆柱的体积V,指出
自变量r 的取值范围.
(2)当r = 5 ,10时,V是多少(结果保留π)?
举
例
例1
图4-2
解
(1) 圆柱的体积 ,自变量r的取值范围
是r > 0.
(2) 当r = 5时, ;
当r = 10 时, .
求下列函数中自变量x的取值范围:
(1) y=3x-1 (2) y=2x2+7
(3) y= (4) y=
(1)因为x取任意实数, 都有意义,所以x的取值范围是任意实数.
(2)因为x取任意实数, 都有意义,所以x的取值范围是任意实数.
(3)因为x+2不等于0时, 才有意义,所以
x的取值范围是:
(4)因为x≥2时, 才有意义,所以x的取值范围是x≥2 .
3、这节课你有什么收获?还有什么疑问?
1、函数是一种“数”吗?
2、在日常生活中,还有哪些量的变化是函数关系?
小 结
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
