湘教版数学七年级下册 1.2.1 代入消元法 教案(表格式)
文档属性
| 名称 | 湘教版数学七年级下册 1.2.1 代入消元法 教案(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 137.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 00:00:00 | ||
图片预览



文档简介
1.2 二元一次方程组的解法
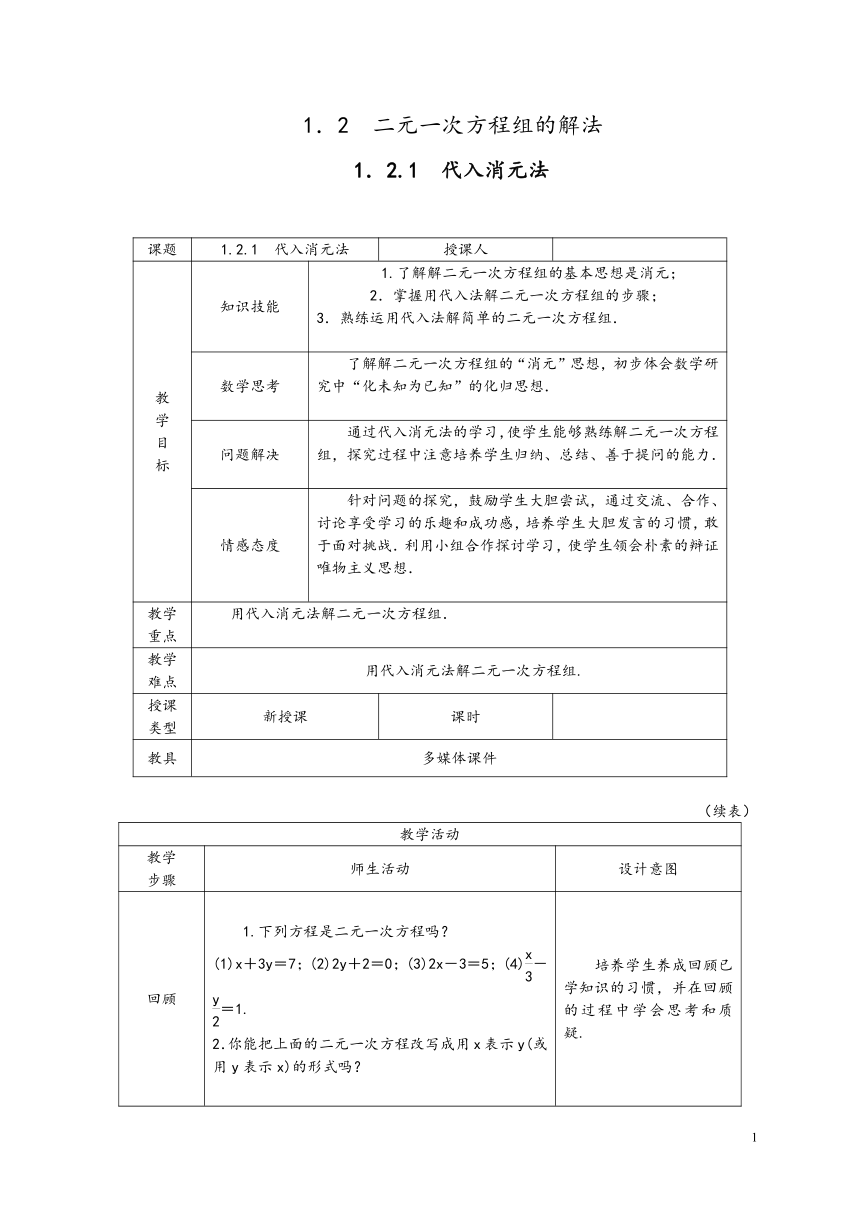
1.2.1 代入消元法
课题 1.2.1 代入消元法 授课人
教学目标 知识技能 1.了解解二元一次方程组的基本思想是消元;2.掌握用代入法解二元一次方程组的步骤;3.熟练运用代入法解简单的二元一次方程组.
数学思考 了解解二元一次方程组的“消元”思想,初步体会数学研究中“化未知为已知”的化归思想.
问题解决 通过代入消元法的学习,使学生能够熟练解二元一次方程组,探究过程中注意培养学生归纳、总结、善于提问的能力.
情感态度 针对问题的探究,鼓励学生大胆尝试,通过交流、合作、讨论享受学习的乐趣和成功感,培养学生大胆发言的习惯,敢于面对挑战.利用小组合作探讨学习,使学生领会朴素的辩证唯物主义思想.
教学重点 用代入消元法解二元一次方程组.
教学难点 用代入消元法解二元一次方程组.
授课类型 新授课 课时
教具 多媒体课件
(续表)
教学活动
教学步骤 师生活动 设计意图
回顾 1.下列方程是二元一次方程吗?(1)x+3y=7;(2)2y+2=0;(3)2x-3=5;(4)-=1.2.你能把上面的二元一次方程改写成用x表示y(或用y表示x)的形式吗? 培养学生养成回顾已学知识的习惯,并在回顾的过程中学会思考和质疑.
活动一:创设情境导入新课 【课堂引入】情境再现:谁的包裹多上节课我们学习了老牛和小马的包裹谁的多的问题,经过大家的共同努力,得出了二元一次方程组到底谁的包裹多呢?这就需要我们解这个二元一次方程组.一元一次方程我们会解,那么二元一次方程组如何解呢? 通过提出这个实际问题,得出解方程组的必要性.充分调动学生的积极性,发挥团结合作精神,展开讨论,来激发学生的学习动机和兴趣.
活动二:实践探究交流新知 【探究】 代入消元法解二元一次方程组问题1:针对上节课老牛和小马驮包裹的问题,你能否列一元一次方程?能求解吗?各小组讨论,共同提出解决问题的方法.再选一个小组代表展示.解:设老牛驮了x个包裹,则小马驮了(x-2)个包裹.根据题意,得x+1=2(x-2-1),x+1=2x-4-2,x-2x=-4-2-1,-x=-7,x=7.问题2:如果设老牛驮了x个包裹,小马驮了y个,你还记得怎么列方程组吗?问题3:如何求出这个方程组的解呢?提示:(1)对照一元一次方程的解法.问题2比问题1多了一个未知数y,y相当于问题1中的________.(2)一元方程会解,那么如何解二元的呢?能否化成一元方程?换句话说,多出来的未知数y可以转化成________,然后代入________.学生自己分析求解,教师规范解题格式问题4:根据分析你能求出这个方程组的解吗?解:由①得y=x-2,③将③代入②,得x+1=2(x-2-1).解得x=7.把x=7入③,得y=5.所以原方程组的解为归纳总结:把方程组其中一个方程的某一个未知数用含有另一个未知数的代数式表示,然后把它代入到另一个方程中,便得到一个一元一次方程.这种解方程组的方法叫做代入消元法,简称代入法.解二元一次方程组的第一种方法——代入消元法,其主要步骤是:第一步:在已知方程组的两个方程中选择一个适当的方程,将它的某个未知数用含有另一个未知数的代数式表示出来.第二步:把此代数式代入没有变形的另一个方程中,可得到一个一元一次方程.第三步:解这个一元一次方程,得到一个未知数的值.第四步:回代求出另一个未知数的值.第五步:把方程组的解表示出来.第六步:检验(口算或在草稿纸上进行笔算),即把求得的解代入每一个方程看是否成立. 通过几个问题引导学生思考如何用代入消元法解二元一次方程组,让学生熟悉用代入消元法解二元一次方程组的解题步骤.
活动三:开放训练体现应用活动三:开放训练体现应用 【应用举例】例1 解方程组:解:将②代入①,得3(y+3)+2y=14.解得y=1.把y=1代入②,得x=4.所以原方程组的解是例2 解方程组:解:由②,得x=13-4y.③将③代入①,得2(13-4y)+3y=16.解得y=2.将y=2代入③,得x=5.所以原方程组的解是变式训练1.已知x+3y-6=0,用含x的代数式表示y为________,用含y的代数式表示x为________.2.已知是方程组的解,则a,b的值是多少?3.如果a3xby与-a2ybx+1是同类项,那么( )A. B. C. D. 通过例题让学生在解答的过程中领会“代入消元法”的真实含义和“化归”的数学思想,进一步熟悉解二元一次方程组的基本思路,熟练解二元一次方程组的基本步骤和过程,并能对二元一次方程组的解进行检验.
【拓展提升】例3 若方程组的解中,x与y相等,则a的值是多少?例4 小明、小亮同时解方程组小明正确解得小亮因抄错了c,解得求a,b,c的值.例5 若方程组与有公共解,求a,b的值. 通过让学生解决数学问题,将新知识融入学生已有的认知结构中.通过检测纠错,使学生能运用所学知识和技能解决问题,同时为学生提供充分发挥创造力的空间,更大程度地调动学生的积极性.
活动四:课堂总结反思 【当堂训练】1.由-=1,可以得到用x表示y的式子是( )A.y= B.y=-C.y=-2 D.y=2-2.解二元一次方程组(1) (2)3.当k为何值时,方程组的解中x与y的值互为相反数? 当堂检测,及时反馈学习效果.
【课堂总结】布置作业:1.教材P8练习T1,T2.2.教材P12习题1.2A组T1. 布置作业,专题突破.
框架图式总结,更容易形成知识网络.
【教学反思】①[授课流程反思]本节课先用一元一次方程和二元一次方程组解决同一个问题,然后通过对比两种方法获得解二元一次方程组的方法,直观、顺畅.接着通过两个例题来规范解题过程,同时整理和提炼解二元一次方程组的思路与方法.②[讲授效果反思]本节课的教学目标是会用代入消元法解二元一次方程组,了解解二元一次方程组的“消元”思想,初步体现数学研究中“化未知为已知”的化归思想.③[师生互动反思]让学生先学,教师再根据问题讲解新课,充分发挥小组合作学习的优势,使得学生的探究有了很好的认知基础,探究显得十分自然流畅,课堂效果很好,学生掌握得也很好.④[习题反思]在巩固练习阶段,注重发挥学生的主体地位,放手让学生练习,然后进行小组交流.好题题号____________________________________________错题题号____________________________________________ 反思,更进一步提升.
代入法解二元一次方程组学案
一课前预习
1. 用代入法解方程组的基本思路怎样?
2. 用代入法解方程组的一般步骤怎样?
二例题欣赏
例1. 用代入法解方程组:
例2.某同学解方程组时,因将第二个方程中的未知数的系数的正负号看错,解得,试求的值。
三课堂练习
1. 解方程组
2. 已知方程组的解为,则__________
四课后练习
1.用代入法解方程组,为计算的方便应该先消去的未知数为_________
2.在下列各组数值中是方程组的解为( )
A) B) C) D)
3.已知是方程组的解,则__________
4.求与的公共解为_________________
5.若满足,则__________
6.解方程组:①; ②; ③
五课后提高练习
7.已知满足,则____________
8.若方程组的解是一对相同的数,则_____________
9.已知方程组的解满足方程,求的值。
1.2.1 代入消元法
课题 1.2.1 代入消元法 授课人
教学目标 知识技能 1.了解解二元一次方程组的基本思想是消元;2.掌握用代入法解二元一次方程组的步骤;3.熟练运用代入法解简单的二元一次方程组.
数学思考 了解解二元一次方程组的“消元”思想,初步体会数学研究中“化未知为已知”的化归思想.
问题解决 通过代入消元法的学习,使学生能够熟练解二元一次方程组,探究过程中注意培养学生归纳、总结、善于提问的能力.
情感态度 针对问题的探究,鼓励学生大胆尝试,通过交流、合作、讨论享受学习的乐趣和成功感,培养学生大胆发言的习惯,敢于面对挑战.利用小组合作探讨学习,使学生领会朴素的辩证唯物主义思想.
教学重点 用代入消元法解二元一次方程组.
教学难点 用代入消元法解二元一次方程组.
授课类型 新授课 课时
教具 多媒体课件
(续表)
教学活动
教学步骤 师生活动 设计意图
回顾 1.下列方程是二元一次方程吗?(1)x+3y=7;(2)2y+2=0;(3)2x-3=5;(4)-=1.2.你能把上面的二元一次方程改写成用x表示y(或用y表示x)的形式吗? 培养学生养成回顾已学知识的习惯,并在回顾的过程中学会思考和质疑.
活动一:创设情境导入新课 【课堂引入】情境再现:谁的包裹多上节课我们学习了老牛和小马的包裹谁的多的问题,经过大家的共同努力,得出了二元一次方程组到底谁的包裹多呢?这就需要我们解这个二元一次方程组.一元一次方程我们会解,那么二元一次方程组如何解呢? 通过提出这个实际问题,得出解方程组的必要性.充分调动学生的积极性,发挥团结合作精神,展开讨论,来激发学生的学习动机和兴趣.
活动二:实践探究交流新知 【探究】 代入消元法解二元一次方程组问题1:针对上节课老牛和小马驮包裹的问题,你能否列一元一次方程?能求解吗?各小组讨论,共同提出解决问题的方法.再选一个小组代表展示.解:设老牛驮了x个包裹,则小马驮了(x-2)个包裹.根据题意,得x+1=2(x-2-1),x+1=2x-4-2,x-2x=-4-2-1,-x=-7,x=7.问题2:如果设老牛驮了x个包裹,小马驮了y个,你还记得怎么列方程组吗?问题3:如何求出这个方程组的解呢?提示:(1)对照一元一次方程的解法.问题2比问题1多了一个未知数y,y相当于问题1中的________.(2)一元方程会解,那么如何解二元的呢?能否化成一元方程?换句话说,多出来的未知数y可以转化成________,然后代入________.学生自己分析求解,教师规范解题格式问题4:根据分析你能求出这个方程组的解吗?解:由①得y=x-2,③将③代入②,得x+1=2(x-2-1).解得x=7.把x=7入③,得y=5.所以原方程组的解为归纳总结:把方程组其中一个方程的某一个未知数用含有另一个未知数的代数式表示,然后把它代入到另一个方程中,便得到一个一元一次方程.这种解方程组的方法叫做代入消元法,简称代入法.解二元一次方程组的第一种方法——代入消元法,其主要步骤是:第一步:在已知方程组的两个方程中选择一个适当的方程,将它的某个未知数用含有另一个未知数的代数式表示出来.第二步:把此代数式代入没有变形的另一个方程中,可得到一个一元一次方程.第三步:解这个一元一次方程,得到一个未知数的值.第四步:回代求出另一个未知数的值.第五步:把方程组的解表示出来.第六步:检验(口算或在草稿纸上进行笔算),即把求得的解代入每一个方程看是否成立. 通过几个问题引导学生思考如何用代入消元法解二元一次方程组,让学生熟悉用代入消元法解二元一次方程组的解题步骤.
活动三:开放训练体现应用活动三:开放训练体现应用 【应用举例】例1 解方程组:解:将②代入①,得3(y+3)+2y=14.解得y=1.把y=1代入②,得x=4.所以原方程组的解是例2 解方程组:解:由②,得x=13-4y.③将③代入①,得2(13-4y)+3y=16.解得y=2.将y=2代入③,得x=5.所以原方程组的解是变式训练1.已知x+3y-6=0,用含x的代数式表示y为________,用含y的代数式表示x为________.2.已知是方程组的解,则a,b的值是多少?3.如果a3xby与-a2ybx+1是同类项,那么( )A. B. C. D. 通过例题让学生在解答的过程中领会“代入消元法”的真实含义和“化归”的数学思想,进一步熟悉解二元一次方程组的基本思路,熟练解二元一次方程组的基本步骤和过程,并能对二元一次方程组的解进行检验.
【拓展提升】例3 若方程组的解中,x与y相等,则a的值是多少?例4 小明、小亮同时解方程组小明正确解得小亮因抄错了c,解得求a,b,c的值.例5 若方程组与有公共解,求a,b的值. 通过让学生解决数学问题,将新知识融入学生已有的认知结构中.通过检测纠错,使学生能运用所学知识和技能解决问题,同时为学生提供充分发挥创造力的空间,更大程度地调动学生的积极性.
活动四:课堂总结反思 【当堂训练】1.由-=1,可以得到用x表示y的式子是( )A.y= B.y=-C.y=-2 D.y=2-2.解二元一次方程组(1) (2)3.当k为何值时,方程组的解中x与y的值互为相反数? 当堂检测,及时反馈学习效果.
【课堂总结】布置作业:1.教材P8练习T1,T2.2.教材P12习题1.2A组T1. 布置作业,专题突破.
框架图式总结,更容易形成知识网络.
【教学反思】①[授课流程反思]本节课先用一元一次方程和二元一次方程组解决同一个问题,然后通过对比两种方法获得解二元一次方程组的方法,直观、顺畅.接着通过两个例题来规范解题过程,同时整理和提炼解二元一次方程组的思路与方法.②[讲授效果反思]本节课的教学目标是会用代入消元法解二元一次方程组,了解解二元一次方程组的“消元”思想,初步体现数学研究中“化未知为已知”的化归思想.③[师生互动反思]让学生先学,教师再根据问题讲解新课,充分发挥小组合作学习的优势,使得学生的探究有了很好的认知基础,探究显得十分自然流畅,课堂效果很好,学生掌握得也很好.④[习题反思]在巩固练习阶段,注重发挥学生的主体地位,放手让学生练习,然后进行小组交流.好题题号____________________________________________错题题号____________________________________________ 反思,更进一步提升.
代入法解二元一次方程组学案
一课前预习
1. 用代入法解方程组的基本思路怎样?
2. 用代入法解方程组的一般步骤怎样?
二例题欣赏
例1. 用代入法解方程组:
例2.某同学解方程组时,因将第二个方程中的未知数的系数的正负号看错,解得,试求的值。
三课堂练习
1. 解方程组
2. 已知方程组的解为,则__________
四课后练习
1.用代入法解方程组,为计算的方便应该先消去的未知数为_________
2.在下列各组数值中是方程组的解为( )
A) B) C) D)
3.已知是方程组的解,则__________
4.求与的公共解为_________________
5.若满足,则__________
6.解方程组:①; ②; ③
五课后提高练习
7.已知满足,则____________
8.若方程组的解是一对相同的数,则_____________
9.已知方程组的解满足方程,求的值。
