湘教版数学七年级下册 2.1.1 同底数幂的乘法 教案(表格式)
文档属性
| 名称 | 湘教版数学七年级下册 2.1.1 同底数幂的乘法 教案(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 88.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 17:43:58 | ||
图片预览




文档简介
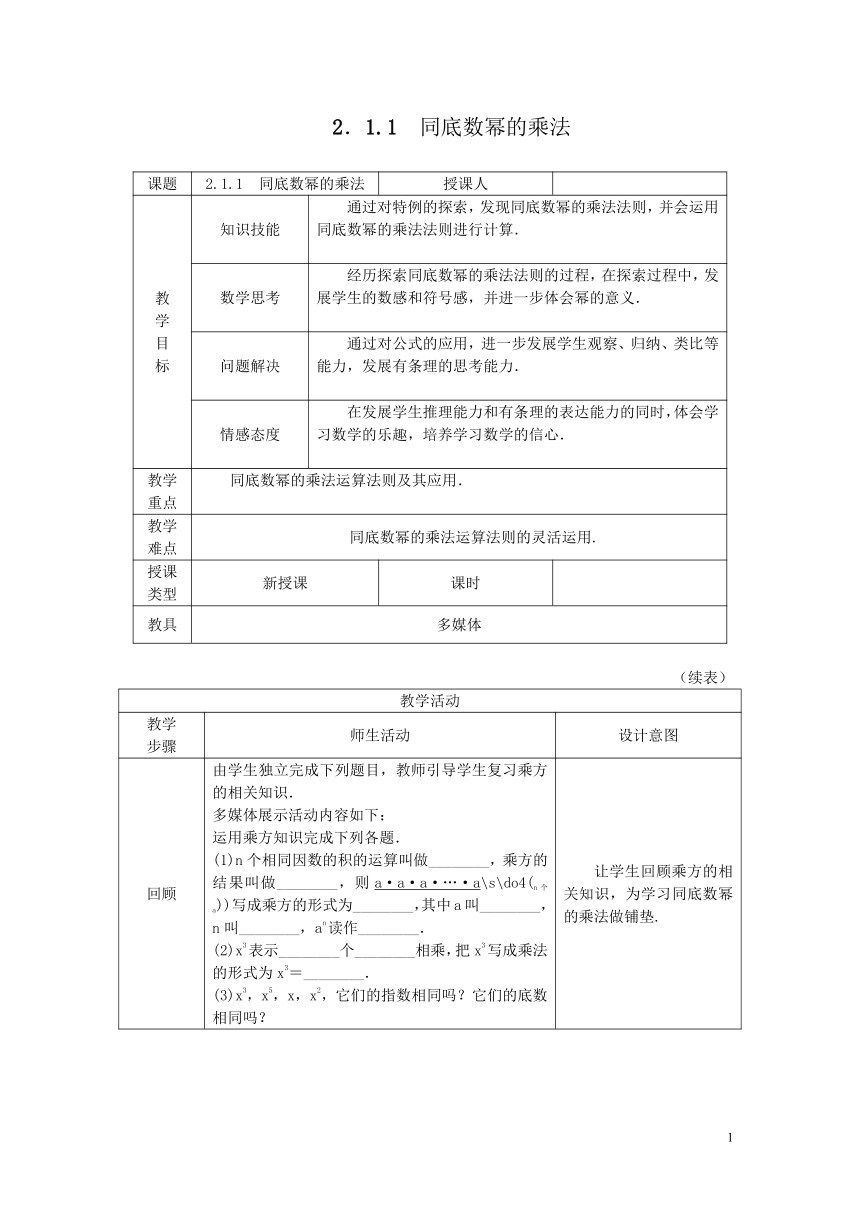
2.1.1 同底数幂的乘法
课题 2.1.1 同底数幂的乘法 授课人
教学目标 知识技能 通过对特例的探索,发现同底数幂的乘法法则,并会运用同底数幂的乘法法则进行计算.
数学思考 经历探索同底数幂的乘法法则的过程,在探索过程中,发展学生的数感和符号感,并进一步体会幂的意义.
问题解决 通过对公式的应用,进一步发展学生观察、归纳、类比等能力,发展有条理的思考能力.
情感态度 在发展学生推理能力和有条理的表达能力的同时,体会学习数学的乐趣,培养学习数学的信心.
教学重点 同底数幂的乘法运算法则及其应用.
教学难点 同底数幂的乘法运算法则的灵活运用.
授课类型 新授课 课时
教具 多媒体
(续表)
教学活动
教学步骤 师生活动 设计意图
回顾 由学生独立完成下列题目,教师引导学生复习乘方的相关知识.多媒体展示活动内容如下:运用乘方知识完成下列各题.(1)n个相同因数的积的运算叫做________,乘方的结果叫做________,则a·a·a·…·a\s\do4(n个a))写成乘方的形式为________,其中a叫________,n叫________,an读作________.(2)x3表示________个________相乘,把x3写成乘法的形式为x3=________.(3)x3,x5,x,x2,它们的指数相同吗?它们的底数相同吗? 让学生回顾乘方的相关知识,为学习同底数幂的乘法做铺垫.
活动一:创设情境导入新课 【课堂引入】1.复习导入(1)an表示的意义是什么?,其中a,n,an分别叫做什么?(2)25表示什么?10×10×10×10×10可以写成什么形式?2.尝试解题,探索规律(1)式子103×102的意义是什么?这个式子中的两个因式有何特点?学生回答:(1)103与102的积;底数相同.(2)一种电子计算机每秒可做108次运算,它工作106秒,一共可做多少次运算?有的学生结果为108×106,有的学生结果为1014. 通过探究问题让学生体会生活中存在着大量的较大的数据,数的世界充满着神奇,期待学生去探索研究.
活动二:实践探究交流新知 【探究】 同底数幂乘法的运算法则108×106=(10×10×…×10)\s\do4(8个))×(10×10×…×10)\s\do4(6个))=1014.仿照上面的运算过程试一试,闯一闯:(1)23×24=(2×2×2)×(2×2×2×2)=2( );(2)73×74=______________=7( );(3)a3·a4=______________=a( );(4)猜一猜:am·an=a( ).各小组学生互相探究、讨论,共同推出结论.思考:当三个或三个以上同底数幂相乘时,是否也具有这一性质呢?归纳总结:同底数幂相乘,底数不变,指数相加,即am·an=am+n(m,n都是正整数),推广:am·an·ap=am+n+p(m,n,p都是正整数). 1.让学生在观察、比较、抽象、概括中总结出同底数幂的乘法运算的本质特征,并猜想出其性质.2.适当拓展,为发展学生思维助力.
活动三:开放训练体现应用活动三:开放训练体现应用 【应用举例】例1 [教材第30页例3] 计算:(1)32×33×34;(2)y·y2·y4.师生活动:注意提示学生a=a1.变式训练1.填空:(1)a·________=a6;(2)x·x3·________=x7;(3)xm·________=x3m;(4)a12=a3·________=________·a5=________·a·a7.2.计算:(1)(a+b)4·(a+b)7;(2)(n-m)5·(n-m)4;(3)(m-n)3·(m-n)5·(m-n)7.学好同底数幂的乘法法则,要注意以下几点:(1)用法则时,首先要看是否同底,底不同就不能直接用;(2)指数相加,而不是相乘;(3)底数不一定只是一个数或一个字母,可以是一个单项式或多项式;(4)底数是互为相反数的两个数时,可以由幂的运算性质变成同底数的幂进行运算;(5)幂的个数可以推广到任意个数. 1.让学生运用性质进行计算,在积累解题经验的同时,体会将同底数幂的乘法运算转化为指数的加法运算的思想.2.变式题可体现知识的延伸,养成提出“新数学问题”的习惯.3.根据做题出现的问题,总结学好同底数幂的乘法法则要注意的事项,为提高学生的运算能力奠定基础.
【拓展提升】例2 计算:2-22-23-24-25-26-27-28-29+210.师生共同分析:注意到210-29=29×2-29×1=29×(2-1)=29,同理,29-28=28,…,23-22=22,即2n+1-2n=2×2n-2n=(2-1)×2n=2n.逆用同底数幂的乘法的运算法则将2n+1化为21×2n即可得解.教师引导学生进行探索,必要时进行适当的启发和提示.例3 已知x4·x3=27,求x的值. 进一步引导学生熟悉知识的综合与拓展,提高学生的应考能力.
活动四:课堂总结反思 【当堂训练】1.(1)计算(口答):①105×106;②a7·a3;③y3·y2;④b5·b;⑤a6·a6;⑥x5·x5.(2)计算:①y2·y6;②x10·x;③x3·x9;④10×102×104;⑤y4·y3·y2·y;⑥x5·x6·x3.学生活动:第(1)题由学生口答;第(2)题在练习本上完成,然后同桌互阅,教师抽查.2.下面的计算对不对?如果不对,应怎样改正?(1)b5·b5=2b5;(2)b5+b5=b10;(3)x5·x5=2x10;(4)x5·x5=x25;(5)c·c3=c3;(6)m+m3=m4.(1)(2)小题强调同底数幂乘法与整式加减的区别;(3)(4)小题强调法则中的“不变”“相加”;(5)小题强调“c”表示“c”的一次幂.3.计算:(1)xn-1·xn+1;(2)(a+b)2·(b+a)3;(3)×.4.若xm-5·x2n-x6=0,则m,n的关系是( )A.m-n=6 B.2m+n=5C.m+2n=11 D.m-2n=7 1.练习以学生抢答的方式完成,注意训练学生的表述能力,以提高兴趣.2.练习主要是对法则运用的强化,形成定式.通过学生对题目的观察、比较、判断,提高学生的是非辨别能力.3.激发学生主动参与的意识,为每一位学生创造在数学学习活动中获得成功的体验机会.
【课堂总结】布置作业:1.教材P30练习第1,2题.2.教材P40习题2.1A组第1,5,6题. 布置作业,专题突破.
活动四:课堂总结反思 框架图式总结,更容易形成知识网络.
【教学反思】①[授课流程反思]在整个教学过程中,把注意力集中在学生身上,充分发挥学生的互动性,激发和鼓励学生的学习探究;提问不仅有序、有提示、有鼓励、有启发,且问在有疑之处.②[讲授效果反思]引导学生注意以下几点:(1)指数相加而不是相乘;(2)负数、分数乘方要加括号;(3)法则逆用要灵活;(4)指数不写代表1次幂.③[师生互动反思]从课堂发言和练习来看,学生在探究同底数幂的乘法法则时,推理能力和有条理的符号表达能力得到了一定的发展.④[习题反思]好题题号____________________________________________错题题号____________________________________________ 反思,更进一步提升.
2.1整式的乘法
1.同底数幂的乘法
学习目标
1、理解同底数幂的乘法法则,能灵活地运用法则进行计算;
2、运用同底数幂的乘法法则解决一些实际问题。
重点: 正确理解同底数幂的乘法法则;
难点: 正确理解和应用同底数幂的乘法法则。
一、创设情境,复习引入
1、求几个_________的____的运算叫做乘方,_________叫做幂,
式子an表示的意义是___________________________
2、把下列式子写成乘方的形式,并指出底数和指数
(-2)×(-2)= ________
(2a)×(2a)×(2a)×(2a)= ________
(a+1)×(a+1)×(a+1)= _________
_________
二、小组探究 得出法则
问题1:一种电子计算机每秒可进行1014次运算,它工作103秒可进行多少次运算?
分析:它工作103秒可进行运算的次数为_________,怎样计算呢
根据乘方的意义可知:1014×103=( )×( )
=( )=1017
问题2: 探究在线
根据乘方的意义填空,看看计算结果有什么规律:
(1)25×22=(2×2×2×2×2)×(2×2)
=(2×2×2×2×2×2×2)=2( )
(2)a3·a2=( )·( )=( )=a( )
(3)5m·5n=5( )
(4)对于任意底数a与任意正整数m,n,
am·an=( )·( )=( )=a( )
法则:同底数的幂相乘,底数 ____ ,指数____ 。
即am·an=a( ) (m,n为正整数)
三、学以致用
1、智取百宝箱(计算下列各题):
(1)(-3)3 × (-3)2 (2) a7 ·a3 (3)xa ·xb
(4)(a-b)2×(a-b)
(6) (-11)5×113
(7) y·ym+1·ym-1
2、我是法官我会判。如果不对,怎样改正?
(1)a3·a3= 2a3( ) (2)b3+b3 = b6 ( )
(3)a2·a3 = a6 ( )
(4)(-5)4×(-5)4= 58 ( )
3、随机应变
(1)x5 ·( )=x 8 (2)a ·( )=a6
(3)x7= x · x3·( ) (4)xm ·( )=x3m
4、实际应用
我国陆地面积约是9.6×106 平方千米。平均每平方千米的土地上,一年从太阳得到的能量相当于燃烧1.3×105 吨煤所产生的能量。求在我国领土上,一年内从太阳得到的能量相当于燃烧多少吨煤所产生的能量。
四、挑战平台
1、把a13写成不同的幂的乘积形式,至少写三种:
2、已知:am=2, an=3.求am+n =? am +3 =?
am+n + 2 =?
3、计算(-2)100 × (-2)99 =
五、小结
我学到了什么?
六、快乐套餐:
自我测验:
1、下面的计算对不对?如果不对,怎样改正?
(1)b5·b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x5 = x25 ( ) (4)y5 ·y5 = 2y10 ( )
(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
2、解答:
(1) (2)(x+y)3 · (x+y)4
3、求X的值
(1) 8 = 2x,则 x = _________
(2) 8× 4 = 2x,则 x = _________
(3) 3×27×9 = 3x,则 x = _________
自我测验:
1、下面的计算对不对?如果不对,怎样改正?
(1)b5·b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x5 = x25 ( ) (4)y5 ·y5 = 2y10 ( )
(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
2、解答:
(1) (2)(x+y)3 · (x+y)4
3、求X的值
(1) 8 = 2x,则 x = _________
(2) 8× 4 = 2x,则 x = _________
(3) 3×27×9 = 3x,则 x = _______
课题 2.1.1 同底数幂的乘法 授课人
教学目标 知识技能 通过对特例的探索,发现同底数幂的乘法法则,并会运用同底数幂的乘法法则进行计算.
数学思考 经历探索同底数幂的乘法法则的过程,在探索过程中,发展学生的数感和符号感,并进一步体会幂的意义.
问题解决 通过对公式的应用,进一步发展学生观察、归纳、类比等能力,发展有条理的思考能力.
情感态度 在发展学生推理能力和有条理的表达能力的同时,体会学习数学的乐趣,培养学习数学的信心.
教学重点 同底数幂的乘法运算法则及其应用.
教学难点 同底数幂的乘法运算法则的灵活运用.
授课类型 新授课 课时
教具 多媒体
(续表)
教学活动
教学步骤 师生活动 设计意图
回顾 由学生独立完成下列题目,教师引导学生复习乘方的相关知识.多媒体展示活动内容如下:运用乘方知识完成下列各题.(1)n个相同因数的积的运算叫做________,乘方的结果叫做________,则a·a·a·…·a\s\do4(n个a))写成乘方的形式为________,其中a叫________,n叫________,an读作________.(2)x3表示________个________相乘,把x3写成乘法的形式为x3=________.(3)x3,x5,x,x2,它们的指数相同吗?它们的底数相同吗? 让学生回顾乘方的相关知识,为学习同底数幂的乘法做铺垫.
活动一:创设情境导入新课 【课堂引入】1.复习导入(1)an表示的意义是什么?,其中a,n,an分别叫做什么?(2)25表示什么?10×10×10×10×10可以写成什么形式?2.尝试解题,探索规律(1)式子103×102的意义是什么?这个式子中的两个因式有何特点?学生回答:(1)103与102的积;底数相同.(2)一种电子计算机每秒可做108次运算,它工作106秒,一共可做多少次运算?有的学生结果为108×106,有的学生结果为1014. 通过探究问题让学生体会生活中存在着大量的较大的数据,数的世界充满着神奇,期待学生去探索研究.
活动二:实践探究交流新知 【探究】 同底数幂乘法的运算法则108×106=(10×10×…×10)\s\do4(8个))×(10×10×…×10)\s\do4(6个))=1014.仿照上面的运算过程试一试,闯一闯:(1)23×24=(2×2×2)×(2×2×2×2)=2( );(2)73×74=______________=7( );(3)a3·a4=______________=a( );(4)猜一猜:am·an=a( ).各小组学生互相探究、讨论,共同推出结论.思考:当三个或三个以上同底数幂相乘时,是否也具有这一性质呢?归纳总结:同底数幂相乘,底数不变,指数相加,即am·an=am+n(m,n都是正整数),推广:am·an·ap=am+n+p(m,n,p都是正整数). 1.让学生在观察、比较、抽象、概括中总结出同底数幂的乘法运算的本质特征,并猜想出其性质.2.适当拓展,为发展学生思维助力.
活动三:开放训练体现应用活动三:开放训练体现应用 【应用举例】例1 [教材第30页例3] 计算:(1)32×33×34;(2)y·y2·y4.师生活动:注意提示学生a=a1.变式训练1.填空:(1)a·________=a6;(2)x·x3·________=x7;(3)xm·________=x3m;(4)a12=a3·________=________·a5=________·a·a7.2.计算:(1)(a+b)4·(a+b)7;(2)(n-m)5·(n-m)4;(3)(m-n)3·(m-n)5·(m-n)7.学好同底数幂的乘法法则,要注意以下几点:(1)用法则时,首先要看是否同底,底不同就不能直接用;(2)指数相加,而不是相乘;(3)底数不一定只是一个数或一个字母,可以是一个单项式或多项式;(4)底数是互为相反数的两个数时,可以由幂的运算性质变成同底数的幂进行运算;(5)幂的个数可以推广到任意个数. 1.让学生运用性质进行计算,在积累解题经验的同时,体会将同底数幂的乘法运算转化为指数的加法运算的思想.2.变式题可体现知识的延伸,养成提出“新数学问题”的习惯.3.根据做题出现的问题,总结学好同底数幂的乘法法则要注意的事项,为提高学生的运算能力奠定基础.
【拓展提升】例2 计算:2-22-23-24-25-26-27-28-29+210.师生共同分析:注意到210-29=29×2-29×1=29×(2-1)=29,同理,29-28=28,…,23-22=22,即2n+1-2n=2×2n-2n=(2-1)×2n=2n.逆用同底数幂的乘法的运算法则将2n+1化为21×2n即可得解.教师引导学生进行探索,必要时进行适当的启发和提示.例3 已知x4·x3=27,求x的值. 进一步引导学生熟悉知识的综合与拓展,提高学生的应考能力.
活动四:课堂总结反思 【当堂训练】1.(1)计算(口答):①105×106;②a7·a3;③y3·y2;④b5·b;⑤a6·a6;⑥x5·x5.(2)计算:①y2·y6;②x10·x;③x3·x9;④10×102×104;⑤y4·y3·y2·y;⑥x5·x6·x3.学生活动:第(1)题由学生口答;第(2)题在练习本上完成,然后同桌互阅,教师抽查.2.下面的计算对不对?如果不对,应怎样改正?(1)b5·b5=2b5;(2)b5+b5=b10;(3)x5·x5=2x10;(4)x5·x5=x25;(5)c·c3=c3;(6)m+m3=m4.(1)(2)小题强调同底数幂乘法与整式加减的区别;(3)(4)小题强调法则中的“不变”“相加”;(5)小题强调“c”表示“c”的一次幂.3.计算:(1)xn-1·xn+1;(2)(a+b)2·(b+a)3;(3)×.4.若xm-5·x2n-x6=0,则m,n的关系是( )A.m-n=6 B.2m+n=5C.m+2n=11 D.m-2n=7 1.练习以学生抢答的方式完成,注意训练学生的表述能力,以提高兴趣.2.练习主要是对法则运用的强化,形成定式.通过学生对题目的观察、比较、判断,提高学生的是非辨别能力.3.激发学生主动参与的意识,为每一位学生创造在数学学习活动中获得成功的体验机会.
【课堂总结】布置作业:1.教材P30练习第1,2题.2.教材P40习题2.1A组第1,5,6题. 布置作业,专题突破.
活动四:课堂总结反思 框架图式总结,更容易形成知识网络.
【教学反思】①[授课流程反思]在整个教学过程中,把注意力集中在学生身上,充分发挥学生的互动性,激发和鼓励学生的学习探究;提问不仅有序、有提示、有鼓励、有启发,且问在有疑之处.②[讲授效果反思]引导学生注意以下几点:(1)指数相加而不是相乘;(2)负数、分数乘方要加括号;(3)法则逆用要灵活;(4)指数不写代表1次幂.③[师生互动反思]从课堂发言和练习来看,学生在探究同底数幂的乘法法则时,推理能力和有条理的符号表达能力得到了一定的发展.④[习题反思]好题题号____________________________________________错题题号____________________________________________ 反思,更进一步提升.
2.1整式的乘法
1.同底数幂的乘法
学习目标
1、理解同底数幂的乘法法则,能灵活地运用法则进行计算;
2、运用同底数幂的乘法法则解决一些实际问题。
重点: 正确理解同底数幂的乘法法则;
难点: 正确理解和应用同底数幂的乘法法则。
一、创设情境,复习引入
1、求几个_________的____的运算叫做乘方,_________叫做幂,
式子an表示的意义是___________________________
2、把下列式子写成乘方的形式,并指出底数和指数
(-2)×(-2)= ________
(2a)×(2a)×(2a)×(2a)= ________
(a+1)×(a+1)×(a+1)= _________
_________
二、小组探究 得出法则
问题1:一种电子计算机每秒可进行1014次运算,它工作103秒可进行多少次运算?
分析:它工作103秒可进行运算的次数为_________,怎样计算呢
根据乘方的意义可知:1014×103=( )×( )
=( )=1017
问题2: 探究在线
根据乘方的意义填空,看看计算结果有什么规律:
(1)25×22=(2×2×2×2×2)×(2×2)
=(2×2×2×2×2×2×2)=2( )
(2)a3·a2=( )·( )=( )=a( )
(3)5m·5n=5( )
(4)对于任意底数a与任意正整数m,n,
am·an=( )·( )=( )=a( )
法则:同底数的幂相乘,底数 ____ ,指数____ 。
即am·an=a( ) (m,n为正整数)
三、学以致用
1、智取百宝箱(计算下列各题):
(1)(-3)3 × (-3)2 (2) a7 ·a3 (3)xa ·xb
(4)(a-b)2×(a-b)
(6) (-11)5×113
(7) y·ym+1·ym-1
2、我是法官我会判。如果不对,怎样改正?
(1)a3·a3= 2a3( ) (2)b3+b3 = b6 ( )
(3)a2·a3 = a6 ( )
(4)(-5)4×(-5)4= 58 ( )
3、随机应变
(1)x5 ·( )=x 8 (2)a ·( )=a6
(3)x7= x · x3·( ) (4)xm ·( )=x3m
4、实际应用
我国陆地面积约是9.6×106 平方千米。平均每平方千米的土地上,一年从太阳得到的能量相当于燃烧1.3×105 吨煤所产生的能量。求在我国领土上,一年内从太阳得到的能量相当于燃烧多少吨煤所产生的能量。
四、挑战平台
1、把a13写成不同的幂的乘积形式,至少写三种:
2、已知:am=2, an=3.求am+n =? am +3 =?
am+n + 2 =?
3、计算(-2)100 × (-2)99 =
五、小结
我学到了什么?
六、快乐套餐:
自我测验:
1、下面的计算对不对?如果不对,怎样改正?
(1)b5·b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x5 = x25 ( ) (4)y5 ·y5 = 2y10 ( )
(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
2、解答:
(1) (2)(x+y)3 · (x+y)4
3、求X的值
(1) 8 = 2x,则 x = _________
(2) 8× 4 = 2x,则 x = _________
(3) 3×27×9 = 3x,则 x = _________
自我测验:
1、下面的计算对不对?如果不对,怎样改正?
(1)b5·b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x5 = x25 ( ) (4)y5 ·y5 = 2y10 ( )
(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
2、解答:
(1) (2)(x+y)3 · (x+y)4
3、求X的值
(1) 8 = 2x,则 x = _________
(2) 8× 4 = 2x,则 x = _________
(3) 3×27×9 = 3x,则 x = _______
