北师大版2021--2022七年级(下)数学第三单元质量检测试卷C(含解析)
文档属性
| 名称 | 北师大版2021--2022七年级(下)数学第三单元质量检测试卷C(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 20:40:38 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
北师大版2021-2022学年七年级(下)第三章变量之间的关系检测试卷C
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1. 下列关于正方形的周长 与边长 之间的关系式 中,有关常量和变量的说法正确的是
A. 是变量, 是常量 B. , 是变量, 是常量
C. , 是变量, 是常量 D. 以上都不对
2. 甲、乙两队参加了“端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程 (米)与时间 (秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是
A. 乙队率先到达终点
B. 甲队比乙队多走了 米
C. 在 秒时,两队所走路程相等
D. 从出发到 秒的时间段内,乙队的速度慢
3. 下面的表格列出了一个实验的统计数据.表示将皮球从高处落下时,弹跳高度 与下降高度 的关系,下面能表示这种关系的式子是
A. B. C. D.
4. 下列曲线中不能表示 是 的函数的是
A. B.
C. D.
5. 某校七年级数学兴趣小组利用同一块木板测量小车从不同高度斜放的木板上从顶部滑到底部所用的时间,支撑物的高度 与小车下滑时间 之间的关系如下表所示:
根据表格提供的信息,下列说法错误的是
A. 支撑物的高度为 时,小车下滑时间为
B. 支撑物的高度 越大,小车下滑时间 越少
C. 若小车下滑时间为 ,则支撑物的高度在 至 之间
D. 若支撑物的高度为 ,则小车下滑时间可以是小于 的任意值
6. 如图,一个函数的图象由射线 ,线段 ,射线 组成,其中点 ,,,,则此函数
A. 当 时, 随 的增大而增大
B. 当 时, 随 的增大而减小
C. 当 时, 随 的增大而增大
D. 当 时, 随 的增大而减小
7. “龟兔赛跑”这则寓言故事讲述的是比赛中兔子开始领先,但它因为骄傲在途中睡觉,而乌龟一直坚持爬行最终赢得比赛,下列函数图象可以体现这一故事过程的是
A. B.
C. D.
8. 以固定的速度 (米/秒)向上抛一个小球,小球的高度 (米)与小球的运动时间 (秒)之间的关系式是 ,在这个关系式中,常量、变量分别为
A. 是常量,, 是变量 B. 是常量,, 是变量
C. , 是常量,, 是变量 D. 是常量,,, 是变量
9. 已知小明从 地到 地,速度为 千米/小时,, 两地相距 千米,若用 (小时)表示行走的时间,(千米)表示余下的路程,则 与 之间的函数表达式是
A. B.
C. D.
10. 下列图象中, 不是 的函数的是
A. B.
C. D.
11. 某科研小组在网上获取了声音在空气中传播的速度与空气温度之间的关系的一些数据(如下表):
下列说法中错误的是
A. 在这个变化过程中,自变量是温度,因变量是声速
B. 温度越高,声速越快
C. 当空气温度为 时, 内声音可以传播
D. 温度每升高 ,声速增加
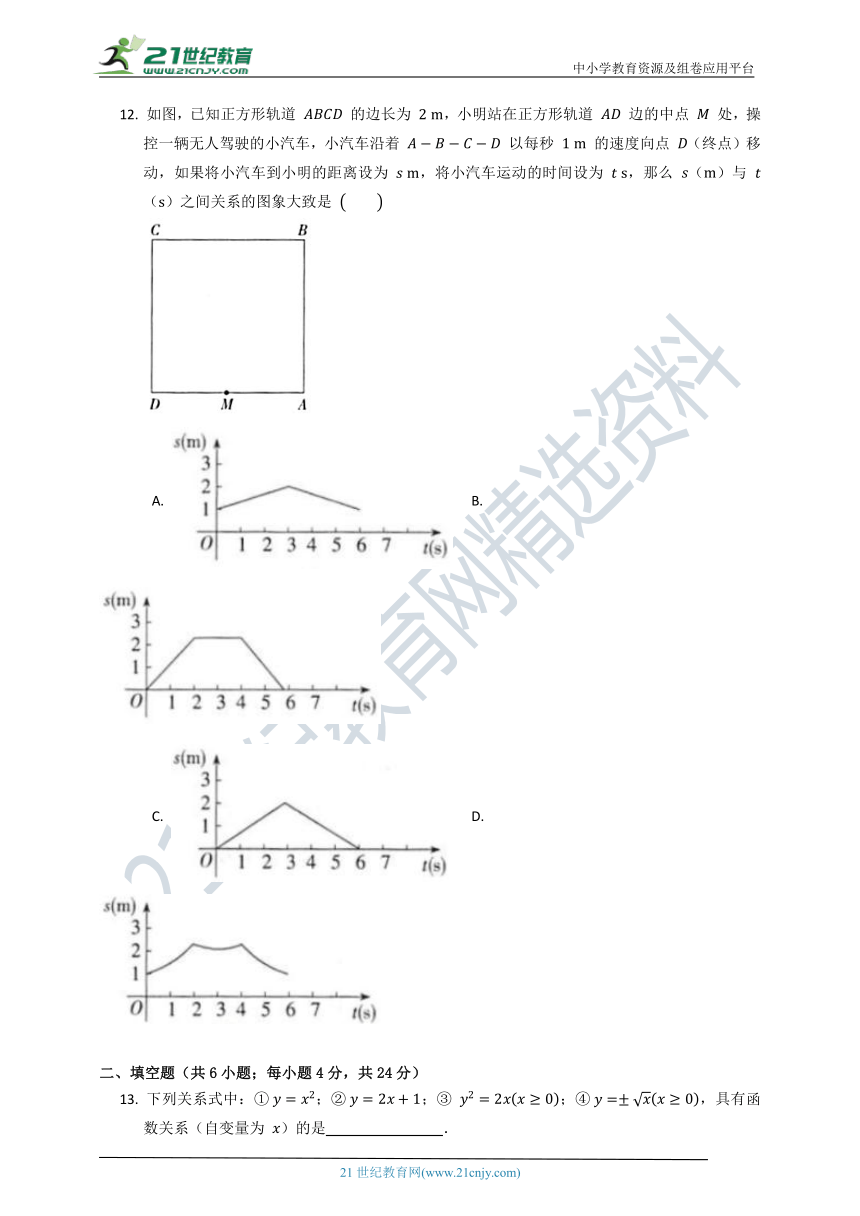
12. 如图,已知正方形轨道 的边长为 ,小明站在正方形轨道 边的中点 处,操控一辆无人驾驶的小汽车,小汽车沿着 以每秒 的速度向点 (终点)移动,如果将小汽车到小明的距离设为 ,将小汽车运动的时间设为 ,那么 ()与 ()之间关系的图象大致是
A. B.
C. D.
二、填空题(共6小题;每小题4分,共24分)
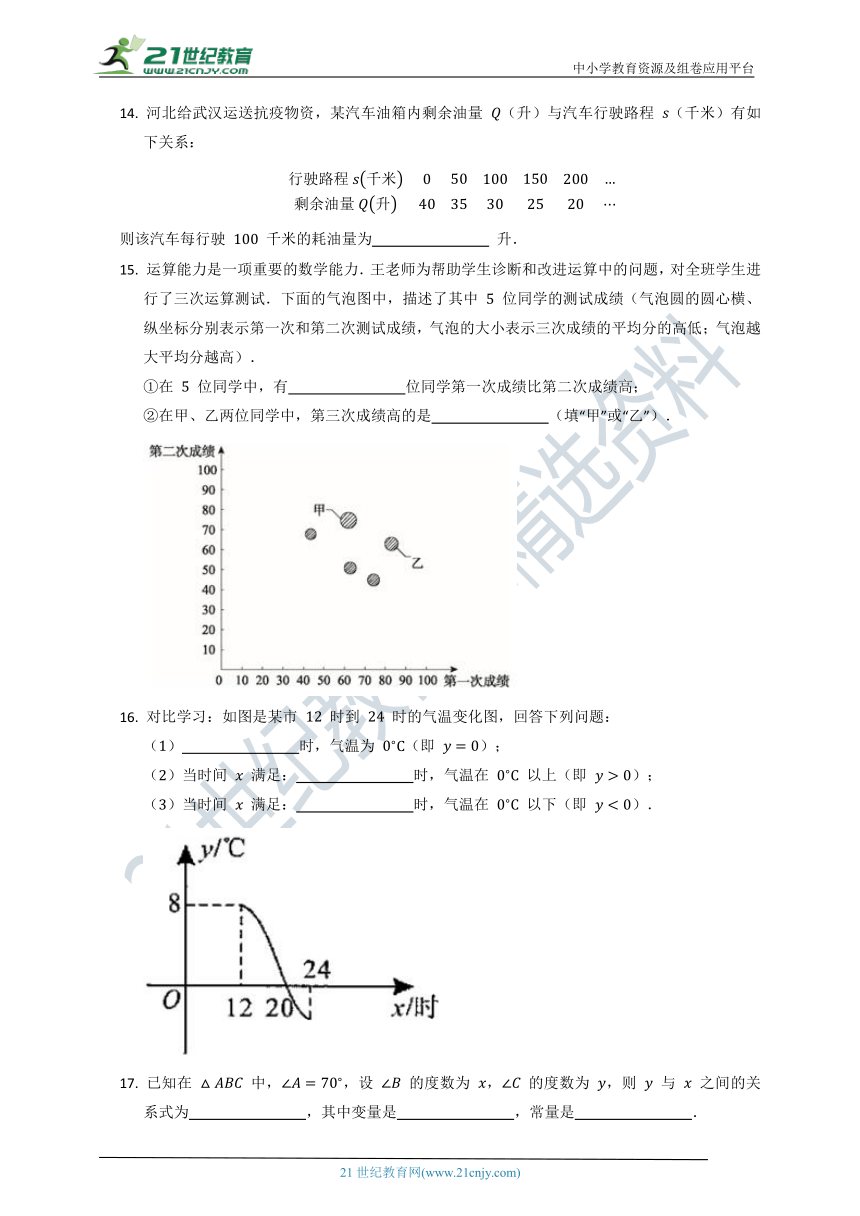
13. 下列关系式中:① ;② ;③ ;④ ,具有函数关系(自变量为 )的是 .
14. 河北给武汉运送抗疫物资,某汽车油箱内剩余油量 (升)与汽车行驶路程 (千米)有如下关系:
则该汽车每行驶 千米的耗油量为 升.
15. 运算能力是一项重要的数学能力.王老师为帮助学生诊断和改进运算中的问题,对全班学生进行了三次运算测试.下面的气泡图中,描述了其中 位同学的测试成绩(气泡圆的圆心横、纵坐标分别表示第一次和第二次测试成绩,气泡的大小表示三次成绩的平均分的高低;气泡越大平均分越高).
①在 位同学中,有 位同学第一次成绩比第二次成绩高;
②在甲、乙两位同学中,第三次成绩高的是 (填“甲”或“乙”).
16. 对比学习:如图是某市 时到 时的气温变化图,回答下列问题:
() 时,气温为 (即 );
()当时间 满足: 时,气温在 以上(即 );
()当时间 满足: 时,气温在 以下(即 ).
17. 已知在 中,,设 的度数为 , 的度数为 ,则 与 之间的关系式为 ,其中变量是 ,常量是 .
18. 已知函数 中,,那么 .
三、解答题(共7小题;共60分)
19. (8分)指出下列关系式中的常量和变量:
(1);
(2).
20. (8分)画出函数 图象.
21. (8分)已知某种蔬菜质量 和单价 (元)之间的关系如下表:
你能将其中某个变量看成另一个变量的函数吗
22. (8分)小华暑假去某地旅游,导游要大家上山时多带一件衣服,并介绍当地山区海拔每上升 米,气温下降 .小华在山脚下看了一下随身携带的温度计,气温为 ,乘缆车到山顶发现气温为 .
(1)试建立气温 ()与缆车上升高度 (米)之间的函数解析式.
(2)估计山脚到山顶的垂直高度.
23. (8分)写出下列各题中的关系式,并指出其中的常量与变量.
(1)底边长为 的三角形的面积 与对应的高 之间的关系式;
(2)某种弹簧原长 厘米,每挂重物 千克,伸长 厘米,在弹性限度范围内,弹簧挂上重物后的长度 (厘米)与所挂重物的质量 (千克)之间的关系式;
(3)购买单价为 元/支的钢笔 支,共花去 元;
(4)全班共有 名同学,其中有 名男同学, 名女同学.
24. (10分)某车间的甲、乙两名工人分别同时生产同种零件,在开始生产的前 个小时为生产磨合期, 个小时后有一人停工一段时间对设备进行改良升级,以提升生产效率,另一人进入正常的生产模式.他们每人生产的零件总数 (个)与生产时间 (小时)的关系如图所示.根据图象回答:
(1)在生产过程中,哪位工人对设备进行改良升级,停止生产多少小时
(2)当 为多少时,甲、乙所生产的零件个数第一次相等 甲、乙中,谁先完成一天的生产任务
(3)设备改良升级后每小时生产零件的个数是多少 与另一工人的正常生产速度相比每小时多生产几个
25. (10分)如图 ,在弧 和弦 所组成的图形中, 是弦 上一动点,过点 作弦 的垂线,交弧 于点 ,连接 .已知 ,设 , 两点间的距离为 ,, 两点间的距离为 ,, 两点间的距离为 .小轩根据学习函数的经验,分别对函数 , 随自变量 的变化而变化的规律进行了探究.下面是小轩的探究过程,请补充完整:
(1)按照下表中自变量 的值进行取点、画图、测量,分别得到了 , 与 的几组对应值:
上表中 的值为 ;(保留两位小数)
(2)在同一平面直角坐标系 (图 )中,函数 的图象如图,请你描出补全后的表中 各组数值所对应的点 并画出函数 的图象;
(3)结合函数图象,解决问题:当 有一个角是 时, 的长度约为 或 .(保留两位小数)
答案
第一部分
1. C
2. C 【解析】A、由函数图象可知,甲走完全程需要 秒,乙走完全程需要 秒,甲队率先到达终点,本选项错误;
B、由函数图象可知,甲、乙两队都走了 米,路程相同,本选项错误;
C、由函数图象可知,在 秒时,两队所走路程相等,均无 米,本选项正确;
D、由函数图象可知,从出发到 秒的时间段内,甲队的速度慢,本选项错误.
3. C
4. C 【解析】A,B,D都满足:对于 ,在它的取值范围内的每一个值, 都有唯一确定的值与它对应,符合函数的定义.
5. D
【解析】从题表中可以看出,随着支撑物高度的增加,小车下滑的时间在减少,支撑物高度为 时,小车下滑的时间一定比 小,但是它是一个固定值,不可以是小于 的任意值.
6. A 【解析】由点 , 可知,当 时, 随 的增大而增大,故A正确;
由 , 知,当 时, 随 的增大而减小,故B错误;
由 , 知,当 时, 随 的增大而增大,故C,D错误.
7. B
8. C
9. D
10. C
【解析】根据函数的定义知,C选项中 不是 的函数.故选C.
11. C 【解析】易知在这个变化过程中,自变量是温度,因变量是声速,
选项A中的说法正确.
根据题表可得,温度越高,声速越快,
选项B中的说法正确.
,
当空气温度为 时, 内声音可以传播 ,
选项C中的说法错误.
,,,,,
温度每升高 ,声速增加 ,
选项D中的说法正确.
12. D 【解析】设小汽车所在的点为点 ,
①当点 在 上运动时,,则 ,此时 ()与 ()之间关系的图象为曲线;
②当点 在 上运动时,同理可得 ,此时 ()与 ()之间关系的图象为曲线;
③当点 在 上运动时,同理可得,图象为曲线.
故选D.
第二部分
13. ①②
【解析】① ;② 中当 取任何值时, 都有唯一的值与之对应.故具有函数关系(自变量为 )的是①②.
14.
【解析】由题表可得,该汽车每行驶 千米的耗油量为 (升).
15. ,甲
16. ,,
17. ,,,
18.
第三部分
19. (1) 常量:;变量: 和
(2) 常量:;变量: 和
20.
21. 可以将 看成 的函数.
22. (1) ;
(2) 米.
23. (1) ,其中 是常量,, 是变量.
(2) ,其中 , 是常量,, 是变量.
(3) ,其中 是常量,, 是变量.
(4) ,其中 是常量,, 是变量.
24. (1) 由图象可知:在生产的过程中,甲进行了改良,停止生产时间: 小时.
(2) 由图象可知,当 时,甲和乙第一次生产零件的个数相同;甲、乙中,甲先完成一天的生产任务.
(3) 设备改良升级后,甲每小时生产零件的个数是: 个;
乙每小时生产零件的个数是: 个;
因此,改良后,甲每小时比乙多生产: 个.
25. (1)
【解析】利用测量法可知:当 时,
,
所以 .
(2) 函数图象如图所示:
(3) ;
【解析】函数 的图象与直线 的交点的横坐标约为 ,
函数 的图象与直线 的交点的横坐标约为 ,
故当 有一个角是 时, 的长度约为 或 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版2021-2022学年七年级(下)第三章变量之间的关系检测试卷C
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1. 下列关于正方形的周长 与边长 之间的关系式 中,有关常量和变量的说法正确的是
A. 是变量, 是常量 B. , 是变量, 是常量
C. , 是变量, 是常量 D. 以上都不对
2. 甲、乙两队参加了“端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程 (米)与时间 (秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是
A. 乙队率先到达终点
B. 甲队比乙队多走了 米
C. 在 秒时,两队所走路程相等
D. 从出发到 秒的时间段内,乙队的速度慢
3. 下面的表格列出了一个实验的统计数据.表示将皮球从高处落下时,弹跳高度 与下降高度 的关系,下面能表示这种关系的式子是
A. B. C. D.
4. 下列曲线中不能表示 是 的函数的是
A. B.
C. D.
5. 某校七年级数学兴趣小组利用同一块木板测量小车从不同高度斜放的木板上从顶部滑到底部所用的时间,支撑物的高度 与小车下滑时间 之间的关系如下表所示:
根据表格提供的信息,下列说法错误的是
A. 支撑物的高度为 时,小车下滑时间为
B. 支撑物的高度 越大,小车下滑时间 越少
C. 若小车下滑时间为 ,则支撑物的高度在 至 之间
D. 若支撑物的高度为 ,则小车下滑时间可以是小于 的任意值
6. 如图,一个函数的图象由射线 ,线段 ,射线 组成,其中点 ,,,,则此函数
A. 当 时, 随 的增大而增大
B. 当 时, 随 的增大而减小
C. 当 时, 随 的增大而增大
D. 当 时, 随 的增大而减小
7. “龟兔赛跑”这则寓言故事讲述的是比赛中兔子开始领先,但它因为骄傲在途中睡觉,而乌龟一直坚持爬行最终赢得比赛,下列函数图象可以体现这一故事过程的是
A. B.
C. D.
8. 以固定的速度 (米/秒)向上抛一个小球,小球的高度 (米)与小球的运动时间 (秒)之间的关系式是 ,在这个关系式中,常量、变量分别为
A. 是常量,, 是变量 B. 是常量,, 是变量
C. , 是常量,, 是变量 D. 是常量,,, 是变量
9. 已知小明从 地到 地,速度为 千米/小时,, 两地相距 千米,若用 (小时)表示行走的时间,(千米)表示余下的路程,则 与 之间的函数表达式是
A. B.
C. D.
10. 下列图象中, 不是 的函数的是
A. B.
C. D.
11. 某科研小组在网上获取了声音在空气中传播的速度与空气温度之间的关系的一些数据(如下表):
下列说法中错误的是
A. 在这个变化过程中,自变量是温度,因变量是声速
B. 温度越高,声速越快
C. 当空气温度为 时, 内声音可以传播
D. 温度每升高 ,声速增加
12. 如图,已知正方形轨道 的边长为 ,小明站在正方形轨道 边的中点 处,操控一辆无人驾驶的小汽车,小汽车沿着 以每秒 的速度向点 (终点)移动,如果将小汽车到小明的距离设为 ,将小汽车运动的时间设为 ,那么 ()与 ()之间关系的图象大致是
A. B.
C. D.
二、填空题(共6小题;每小题4分,共24分)
13. 下列关系式中:① ;② ;③ ;④ ,具有函数关系(自变量为 )的是 .
14. 河北给武汉运送抗疫物资,某汽车油箱内剩余油量 (升)与汽车行驶路程 (千米)有如下关系:
则该汽车每行驶 千米的耗油量为 升.
15. 运算能力是一项重要的数学能力.王老师为帮助学生诊断和改进运算中的问题,对全班学生进行了三次运算测试.下面的气泡图中,描述了其中 位同学的测试成绩(气泡圆的圆心横、纵坐标分别表示第一次和第二次测试成绩,气泡的大小表示三次成绩的平均分的高低;气泡越大平均分越高).
①在 位同学中,有 位同学第一次成绩比第二次成绩高;
②在甲、乙两位同学中,第三次成绩高的是 (填“甲”或“乙”).
16. 对比学习:如图是某市 时到 时的气温变化图,回答下列问题:
() 时,气温为 (即 );
()当时间 满足: 时,气温在 以上(即 );
()当时间 满足: 时,气温在 以下(即 ).
17. 已知在 中,,设 的度数为 , 的度数为 ,则 与 之间的关系式为 ,其中变量是 ,常量是 .
18. 已知函数 中,,那么 .
三、解答题(共7小题;共60分)
19. (8分)指出下列关系式中的常量和变量:
(1);
(2).
20. (8分)画出函数 图象.
21. (8分)已知某种蔬菜质量 和单价 (元)之间的关系如下表:
你能将其中某个变量看成另一个变量的函数吗
22. (8分)小华暑假去某地旅游,导游要大家上山时多带一件衣服,并介绍当地山区海拔每上升 米,气温下降 .小华在山脚下看了一下随身携带的温度计,气温为 ,乘缆车到山顶发现气温为 .
(1)试建立气温 ()与缆车上升高度 (米)之间的函数解析式.
(2)估计山脚到山顶的垂直高度.
23. (8分)写出下列各题中的关系式,并指出其中的常量与变量.
(1)底边长为 的三角形的面积 与对应的高 之间的关系式;
(2)某种弹簧原长 厘米,每挂重物 千克,伸长 厘米,在弹性限度范围内,弹簧挂上重物后的长度 (厘米)与所挂重物的质量 (千克)之间的关系式;
(3)购买单价为 元/支的钢笔 支,共花去 元;
(4)全班共有 名同学,其中有 名男同学, 名女同学.
24. (10分)某车间的甲、乙两名工人分别同时生产同种零件,在开始生产的前 个小时为生产磨合期, 个小时后有一人停工一段时间对设备进行改良升级,以提升生产效率,另一人进入正常的生产模式.他们每人生产的零件总数 (个)与生产时间 (小时)的关系如图所示.根据图象回答:
(1)在生产过程中,哪位工人对设备进行改良升级,停止生产多少小时
(2)当 为多少时,甲、乙所生产的零件个数第一次相等 甲、乙中,谁先完成一天的生产任务
(3)设备改良升级后每小时生产零件的个数是多少 与另一工人的正常生产速度相比每小时多生产几个
25. (10分)如图 ,在弧 和弦 所组成的图形中, 是弦 上一动点,过点 作弦 的垂线,交弧 于点 ,连接 .已知 ,设 , 两点间的距离为 ,, 两点间的距离为 ,, 两点间的距离为 .小轩根据学习函数的经验,分别对函数 , 随自变量 的变化而变化的规律进行了探究.下面是小轩的探究过程,请补充完整:
(1)按照下表中自变量 的值进行取点、画图、测量,分别得到了 , 与 的几组对应值:
上表中 的值为 ;(保留两位小数)
(2)在同一平面直角坐标系 (图 )中,函数 的图象如图,请你描出补全后的表中 各组数值所对应的点 并画出函数 的图象;
(3)结合函数图象,解决问题:当 有一个角是 时, 的长度约为 或 .(保留两位小数)
答案
第一部分
1. C
2. C 【解析】A、由函数图象可知,甲走完全程需要 秒,乙走完全程需要 秒,甲队率先到达终点,本选项错误;
B、由函数图象可知,甲、乙两队都走了 米,路程相同,本选项错误;
C、由函数图象可知,在 秒时,两队所走路程相等,均无 米,本选项正确;
D、由函数图象可知,从出发到 秒的时间段内,甲队的速度慢,本选项错误.
3. C
4. C 【解析】A,B,D都满足:对于 ,在它的取值范围内的每一个值, 都有唯一确定的值与它对应,符合函数的定义.
5. D
【解析】从题表中可以看出,随着支撑物高度的增加,小车下滑的时间在减少,支撑物高度为 时,小车下滑的时间一定比 小,但是它是一个固定值,不可以是小于 的任意值.
6. A 【解析】由点 , 可知,当 时, 随 的增大而增大,故A正确;
由 , 知,当 时, 随 的增大而减小,故B错误;
由 , 知,当 时, 随 的增大而增大,故C,D错误.
7. B
8. C
9. D
10. C
【解析】根据函数的定义知,C选项中 不是 的函数.故选C.
11. C 【解析】易知在这个变化过程中,自变量是温度,因变量是声速,
选项A中的说法正确.
根据题表可得,温度越高,声速越快,
选项B中的说法正确.
,
当空气温度为 时, 内声音可以传播 ,
选项C中的说法错误.
,,,,,
温度每升高 ,声速增加 ,
选项D中的说法正确.
12. D 【解析】设小汽车所在的点为点 ,
①当点 在 上运动时,,则 ,此时 ()与 ()之间关系的图象为曲线;
②当点 在 上运动时,同理可得 ,此时 ()与 ()之间关系的图象为曲线;
③当点 在 上运动时,同理可得,图象为曲线.
故选D.
第二部分
13. ①②
【解析】① ;② 中当 取任何值时, 都有唯一的值与之对应.故具有函数关系(自变量为 )的是①②.
14.
【解析】由题表可得,该汽车每行驶 千米的耗油量为 (升).
15. ,甲
16. ,,
17. ,,,
18.
第三部分
19. (1) 常量:;变量: 和
(2) 常量:;变量: 和
20.
21. 可以将 看成 的函数.
22. (1) ;
(2) 米.
23. (1) ,其中 是常量,, 是变量.
(2) ,其中 , 是常量,, 是变量.
(3) ,其中 是常量,, 是变量.
(4) ,其中 是常量,, 是变量.
24. (1) 由图象可知:在生产的过程中,甲进行了改良,停止生产时间: 小时.
(2) 由图象可知,当 时,甲和乙第一次生产零件的个数相同;甲、乙中,甲先完成一天的生产任务.
(3) 设备改良升级后,甲每小时生产零件的个数是: 个;
乙每小时生产零件的个数是: 个;
因此,改良后,甲每小时比乙多生产: 个.
25. (1)
【解析】利用测量法可知:当 时,
,
所以 .
(2) 函数图象如图所示:
(3) ;
【解析】函数 的图象与直线 的交点的横坐标约为 ,
函数 的图象与直线 的交点的横坐标约为 ,
故当 有一个角是 时, 的长度约为 或 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
