湘教版数学七年级下册 4.3 平行线的性质 教案(表格式)
文档属性
| 名称 | 湘教版数学七年级下册 4.3 平行线的性质 教案(表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 431.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 18:01:53 | ||
图片预览



文档简介
4.3 平行线的性质
课题 4.3 平行线的性质 授课人
教学目标 知识技能 1.掌握平行线的性质1:两直线平行,同位角相等.了解此性质的推出过程.2.探索并能推理下面两条性质:两直线平行,内错角相等;两直线平行,同旁内角互补.
数学思考 经历探索平行线的性质定理的推理过程,培养学生的观察、分析和进行简单的逻辑推理的能力.
问题解决 结合图形,用符号语言来表示平行线的三条性质的条件和结论.并能总结归纳出推理的一般步骤.
情感态度 培养学生合作探究的学习方法,体会互逆的思维过程和几何中的应用价值.
教学重点 平行线的性质1,2,3的推理.
教学难点 平行线的性质1的探索与推理.
授课类型 新授课 课时
教具 多媒体课件
教学活动
教学步骤 师生活动 设计意图
活动一:创设情境导入新课 【课堂引入】为了实施南水北调工程,国家决定实施“引长江水进城市”的工程.在修建某引水渠时,遇上A,B之间有座大山,经勘探表明引水渠若从山中穿过,既安全又节省开支,于是决定开凿涵洞,在A地测得涵洞走向是北偏东66°28′,如图4-3-9,如果A,B两地同时施工,那么B地按南偏西多少度施工,才能使涵洞在山脉中呈直线准确接通?图4-3-9 通过现实情景再现,让学生体会到数学来源于生活,培养学生良好的数学应用意识.训练学生独立思考,分析和推理表达的能力,同时将问题转化为已知两条直线平行,确定内错角之间的关系,从而引出本节课课题.
活动二:实践探究交流新知 【探究1】 平行线的性质1:两直线平行,同位角相等(1)教室的窗户的横格是平行的,请看老师用三角尺去检验一对同位角,看看结果怎样?(教师用三角尺在窗户上演示,学生观察并思考)(2)学生试验(发印好平行线的纸单)已知:a∥b,任意画一条直线c与平行线a,b相交.任选一对同位角,用适当的方法试验,看看这一对同位角有什么关系.(要求学生多画几条截线试试,鼓励学生用多种方法进行探索)图4-3-10(3)在几何画板中演示和观察方法:多媒体演示几何画板作图,让图中直线c旋转,而直线a,b不动,分别度量各角,请同学观察同位角有无变化,进而得出平行线的特征.归纳总结:两条平行线被第三条直线所截,同位角相等.简记为“两直线平行,同位角相等”.【探究2】 平行线的性质2:两直线平行线,内错角相等如图4-3-11,已知:直线a∥b,∠1和∠2是直线a,b被直线c截出的内错角.思考:∠1与∠2有什么样的数量关系?图4-3-11引导学生推理:∵a∥b(已知),∴∠3=∠2(两直线平行,同位角相等).∵∠1=∠3(对顶角相等),∴∠1=∠2(等量代换).归纳总结:两条平行线被第三条直线所截,内错角相等.简记为“两直线平行,内错角相等”.【探究3】 平行线的性质3:两直线平行,同旁内角互补仿照【探究2】,如图4-3-12,已知:a∥b,∠1与∠2有什么样的数量关系?你能用所学的知识加以说明吗?图4-3-12试试看,各小组合作共同完成.解:∵a∥b(已知),∴∠3=∠2(两直线平行,内错角相等).∵∠1+∠3=180°,∴∠1+∠2=180°(等量代换).归纳总结:两条平行线被第三条直线所截,同旁内角互补.简记为“两直线平行,同旁内角互补”. 通过对平行线性质的探索,使学生对推理的步骤、格式有更进一步的认识,认识推理的必要性,充分调动学生的主动性和积极性,进而培养学生分析问题的能力,在学生有成就感的同时,也激励了他们的学习兴趣.
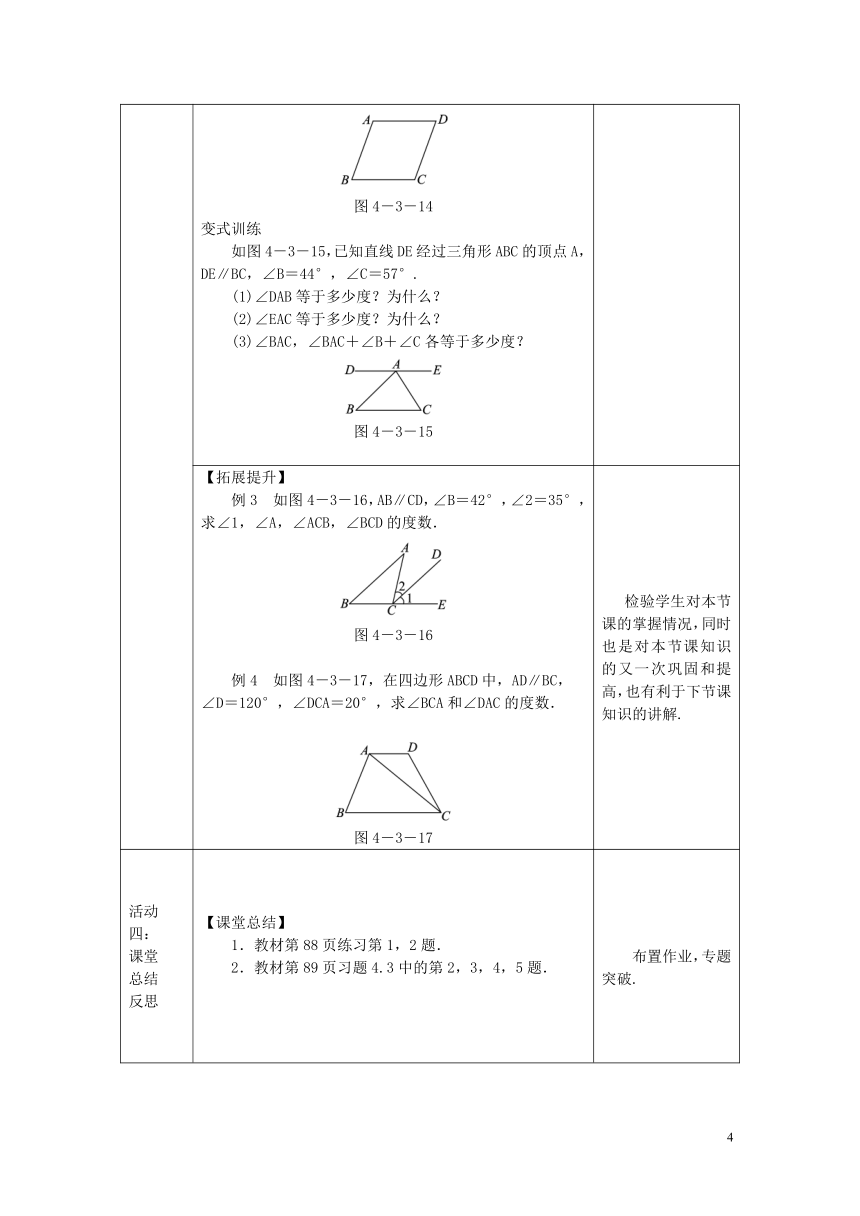
活动三:开放训练体现应用 【应用举例】例1 如图4-3-13,直线AB,CD被直线EF所截,AB∥CD,∠1=100°,试求∠3的度数.图4-3-13例2 如图4-3-14,AD∥BC,∠B=∠D,试问∠A与∠C相等吗?为什么?图4-3-14变式训练如图4-3-15,已知直线DE经过三角形ABC的顶点A,DE∥BC,∠B=44°,∠C=57°.(1)∠DAB等于多少度?为什么?(2)∠EAC等于多少度?为什么?(3)∠BAC,∠BAC+∠B+∠C各等于多少度?图4-3-15 通过学生对推理的螺旋式上升的认识,更认识到数学严密性与推理的必要性,做到每一步都有根有据.
【拓展提升】例3 如图4-3-16,AB∥CD,∠B=42°,∠2=35°,求∠1,∠A,∠ACB,∠BCD的度数.图4-3-16 例4 如图4-3-17,在四边形ABCD中,AD∥BC,∠D=120°,∠DCA=20°,求∠BCA和∠DAC的度数.图4-3-17 检验学生对本节课的掌握情况,同时也是对本节课知识的又一次巩固和提高,也有利于下节课知识的讲解.
活动四:课堂总结反思活动四:课堂总结反思 【课堂总结】1.教材第88页练习第1,2题.2.教材第89页习题4.3中的第2,3,4,5题. 布置作业,专题突破.
【知识网络】 框架图式总结,更容易形成知识网络.
【教学反思】①[授课流程反思]通过生活中的事例,让学生感受数学来源于生活,通过问题的设置,训练学生的语言表达的准确性和简洁性,提供给学生充分进行数学活动和探索的机会,让学生在轻松愉快中掌握推理的步骤和格式.②[讲授效果反思]语言是思维的工具,要学好推理说明,必须学会语言的表达和运用,初学时,学生对几何语言不甚清楚,几何语言分为文字语言、符号语言和图形语言,教师有必要强调:将图形语言和符号语言相结合是学好证明的基本功,画图时按要求将符合题意的图形画出来.但要注意以下几点:(1)注意所画图形的多种情况;(2)能根据题意画出简单的图形,掌握“题”与“图”的对应关系,一般图形不要画成特殊图形,否则就意味着人为增加了已知条件,反之,特殊图形也不要画成一般图形,这两种做法都没有真实的表达题意;(3)图形力求准确,便于观察,有利于解题.③[师生互动反思] ④[习题反思]好题题号 错题题号 反思,更进一步提升.
4.3 平行线的性质
学习目标:
1.理解:平行线的性质.
2.掌握:平行线的性质.
3.应用:会用平行线的性质进行推理和计算.
课标目标:会用平行线的性质进行推理和计算
学习重点:平行线的性质公理及平行线性质定理的推理.
1、 学前准备:
1.如图,
(1)∵∠1______∠2(已知),∴a∥b( )
(2)∵∠2______∠3(已知),∴a∥b( )
(3)∵∠2+∠4=______(已知),∴a∥b( )
2.如图,一条公路两次拐弯后,和原来的方向相同,第一次拐的角∠B是142°,第二次拐的角∠C是多少度?
二、自学指导
阅读教科书,回答问题
平行线的性质:
1? 两直线平行,______角相等。
2? 两直线平行,______角相等。
3? 两直线平行,同旁内角______。
三、例题讲解
例4 如图,已知直线a∥b,∠1=50°,求∠2的度数。
解
例5 如图,在四边形ABCD中,已知AB∥CD,∠B=60°,求∠C的度数。能否求得∠A的度数?
解
四、课堂练习
1.在下列解答中,填空:
(1)∵AD∥BC(已知),
∴∠____+∠ABC =180°(两直线平行,同旁内角互补);
(2)∵AB∥CD(已知),
∴∠____+∠ABC =180°(两直线平行,同旁内角互补);
2.在图上画着与第三条直线相交的两条平行线。已知∠1等于52°,那么
∠2=______,∠3=______,∠4=______。
五、学习体会
六、堂清
在下列解答中,填上适当的理由:
(1)∵AD∥BC(已知),
∴∠B=∠1( );
(2)∵AB∥CD(已知),
∴∠D=∠1( );
七、课后作业
1.如图,已知直线DE经过点A,DE∥BC,∠B=44°,∠C=57°
(1)∠DAB等于多少度?为什么?
(2)∠EAC等于多少度?为什么?
(3)∠BAC、∠BAC+∠B+∠C各等于多少度?
2.如图,A、B、C、D在直线上,AD∥EF.
(1)∠E=78°时,∠1、∠2各等于多少度?为什么?
(2)∠F=58°时,∠3、∠4各等于多少度?为什么?
3.画出将如图所示的方格纸中的图形向右平移3格,并向下平移4格后的图形。
(第3题) (第4题)
4.如图,已知直线a∥b,∠3=131°,求∠1、∠2的度数,抄写下面的解答过程,并填空或填写适当的理由。
解∵∠3=131°( ),
又∵∠3=∠1( ),
∴∠1 =______( );
∵a∥b( ),
∴∠1+∠2 =180°( );
∴∠2 =______(等式的性质)。
课题 4.3 平行线的性质 授课人
教学目标 知识技能 1.掌握平行线的性质1:两直线平行,同位角相等.了解此性质的推出过程.2.探索并能推理下面两条性质:两直线平行,内错角相等;两直线平行,同旁内角互补.
数学思考 经历探索平行线的性质定理的推理过程,培养学生的观察、分析和进行简单的逻辑推理的能力.
问题解决 结合图形,用符号语言来表示平行线的三条性质的条件和结论.并能总结归纳出推理的一般步骤.
情感态度 培养学生合作探究的学习方法,体会互逆的思维过程和几何中的应用价值.
教学重点 平行线的性质1,2,3的推理.
教学难点 平行线的性质1的探索与推理.
授课类型 新授课 课时
教具 多媒体课件
教学活动
教学步骤 师生活动 设计意图
活动一:创设情境导入新课 【课堂引入】为了实施南水北调工程,国家决定实施“引长江水进城市”的工程.在修建某引水渠时,遇上A,B之间有座大山,经勘探表明引水渠若从山中穿过,既安全又节省开支,于是决定开凿涵洞,在A地测得涵洞走向是北偏东66°28′,如图4-3-9,如果A,B两地同时施工,那么B地按南偏西多少度施工,才能使涵洞在山脉中呈直线准确接通?图4-3-9 通过现实情景再现,让学生体会到数学来源于生活,培养学生良好的数学应用意识.训练学生独立思考,分析和推理表达的能力,同时将问题转化为已知两条直线平行,确定内错角之间的关系,从而引出本节课课题.
活动二:实践探究交流新知 【探究1】 平行线的性质1:两直线平行,同位角相等(1)教室的窗户的横格是平行的,请看老师用三角尺去检验一对同位角,看看结果怎样?(教师用三角尺在窗户上演示,学生观察并思考)(2)学生试验(发印好平行线的纸单)已知:a∥b,任意画一条直线c与平行线a,b相交.任选一对同位角,用适当的方法试验,看看这一对同位角有什么关系.(要求学生多画几条截线试试,鼓励学生用多种方法进行探索)图4-3-10(3)在几何画板中演示和观察方法:多媒体演示几何画板作图,让图中直线c旋转,而直线a,b不动,分别度量各角,请同学观察同位角有无变化,进而得出平行线的特征.归纳总结:两条平行线被第三条直线所截,同位角相等.简记为“两直线平行,同位角相等”.【探究2】 平行线的性质2:两直线平行线,内错角相等如图4-3-11,已知:直线a∥b,∠1和∠2是直线a,b被直线c截出的内错角.思考:∠1与∠2有什么样的数量关系?图4-3-11引导学生推理:∵a∥b(已知),∴∠3=∠2(两直线平行,同位角相等).∵∠1=∠3(对顶角相等),∴∠1=∠2(等量代换).归纳总结:两条平行线被第三条直线所截,内错角相等.简记为“两直线平行,内错角相等”.【探究3】 平行线的性质3:两直线平行,同旁内角互补仿照【探究2】,如图4-3-12,已知:a∥b,∠1与∠2有什么样的数量关系?你能用所学的知识加以说明吗?图4-3-12试试看,各小组合作共同完成.解:∵a∥b(已知),∴∠3=∠2(两直线平行,内错角相等).∵∠1+∠3=180°,∴∠1+∠2=180°(等量代换).归纳总结:两条平行线被第三条直线所截,同旁内角互补.简记为“两直线平行,同旁内角互补”. 通过对平行线性质的探索,使学生对推理的步骤、格式有更进一步的认识,认识推理的必要性,充分调动学生的主动性和积极性,进而培养学生分析问题的能力,在学生有成就感的同时,也激励了他们的学习兴趣.
活动三:开放训练体现应用 【应用举例】例1 如图4-3-13,直线AB,CD被直线EF所截,AB∥CD,∠1=100°,试求∠3的度数.图4-3-13例2 如图4-3-14,AD∥BC,∠B=∠D,试问∠A与∠C相等吗?为什么?图4-3-14变式训练如图4-3-15,已知直线DE经过三角形ABC的顶点A,DE∥BC,∠B=44°,∠C=57°.(1)∠DAB等于多少度?为什么?(2)∠EAC等于多少度?为什么?(3)∠BAC,∠BAC+∠B+∠C各等于多少度?图4-3-15 通过学生对推理的螺旋式上升的认识,更认识到数学严密性与推理的必要性,做到每一步都有根有据.
【拓展提升】例3 如图4-3-16,AB∥CD,∠B=42°,∠2=35°,求∠1,∠A,∠ACB,∠BCD的度数.图4-3-16 例4 如图4-3-17,在四边形ABCD中,AD∥BC,∠D=120°,∠DCA=20°,求∠BCA和∠DAC的度数.图4-3-17 检验学生对本节课的掌握情况,同时也是对本节课知识的又一次巩固和提高,也有利于下节课知识的讲解.
活动四:课堂总结反思活动四:课堂总结反思 【课堂总结】1.教材第88页练习第1,2题.2.教材第89页习题4.3中的第2,3,4,5题. 布置作业,专题突破.
【知识网络】 框架图式总结,更容易形成知识网络.
【教学反思】①[授课流程反思]通过生活中的事例,让学生感受数学来源于生活,通过问题的设置,训练学生的语言表达的准确性和简洁性,提供给学生充分进行数学活动和探索的机会,让学生在轻松愉快中掌握推理的步骤和格式.②[讲授效果反思]语言是思维的工具,要学好推理说明,必须学会语言的表达和运用,初学时,学生对几何语言不甚清楚,几何语言分为文字语言、符号语言和图形语言,教师有必要强调:将图形语言和符号语言相结合是学好证明的基本功,画图时按要求将符合题意的图形画出来.但要注意以下几点:(1)注意所画图形的多种情况;(2)能根据题意画出简单的图形,掌握“题”与“图”的对应关系,一般图形不要画成特殊图形,否则就意味着人为增加了已知条件,反之,特殊图形也不要画成一般图形,这两种做法都没有真实的表达题意;(3)图形力求准确,便于观察,有利于解题.③[师生互动反思] ④[习题反思]好题题号 错题题号 反思,更进一步提升.
4.3 平行线的性质
学习目标:
1.理解:平行线的性质.
2.掌握:平行线的性质.
3.应用:会用平行线的性质进行推理和计算.
课标目标:会用平行线的性质进行推理和计算
学习重点:平行线的性质公理及平行线性质定理的推理.
1、 学前准备:
1.如图,
(1)∵∠1______∠2(已知),∴a∥b( )
(2)∵∠2______∠3(已知),∴a∥b( )
(3)∵∠2+∠4=______(已知),∴a∥b( )
2.如图,一条公路两次拐弯后,和原来的方向相同,第一次拐的角∠B是142°,第二次拐的角∠C是多少度?
二、自学指导
阅读教科书,回答问题
平行线的性质:
1? 两直线平行,______角相等。
2? 两直线平行,______角相等。
3? 两直线平行,同旁内角______。
三、例题讲解
例4 如图,已知直线a∥b,∠1=50°,求∠2的度数。
解
例5 如图,在四边形ABCD中,已知AB∥CD,∠B=60°,求∠C的度数。能否求得∠A的度数?
解
四、课堂练习
1.在下列解答中,填空:
(1)∵AD∥BC(已知),
∴∠____+∠ABC =180°(两直线平行,同旁内角互补);
(2)∵AB∥CD(已知),
∴∠____+∠ABC =180°(两直线平行,同旁内角互补);
2.在图上画着与第三条直线相交的两条平行线。已知∠1等于52°,那么
∠2=______,∠3=______,∠4=______。
五、学习体会
六、堂清
在下列解答中,填上适当的理由:
(1)∵AD∥BC(已知),
∴∠B=∠1( );
(2)∵AB∥CD(已知),
∴∠D=∠1( );
七、课后作业
1.如图,已知直线DE经过点A,DE∥BC,∠B=44°,∠C=57°
(1)∠DAB等于多少度?为什么?
(2)∠EAC等于多少度?为什么?
(3)∠BAC、∠BAC+∠B+∠C各等于多少度?
2.如图,A、B、C、D在直线上,AD∥EF.
(1)∠E=78°时,∠1、∠2各等于多少度?为什么?
(2)∠F=58°时,∠3、∠4各等于多少度?为什么?
3.画出将如图所示的方格纸中的图形向右平移3格,并向下平移4格后的图形。
(第3题) (第4题)
4.如图,已知直线a∥b,∠3=131°,求∠1、∠2的度数,抄写下面的解答过程,并填空或填写适当的理由。
解∵∠3=131°( ),
又∵∠3=∠1( ),
∴∠1 =______( );
∵a∥b( ),
∴∠1+∠2 =180°( );
∴∠2 =______(等式的性质)。
