湘教版九年级数学下册第二章《圆》2.5.2切线长定理 课件(共20张PPT)
文档属性
| 名称 | 湘教版九年级数学下册第二章《圆》2.5.2切线长定理 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 257.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 14:23:39 | ||
图片预览


文档简介
(共20张PPT)
切线长定理
学习目标:
1、理解切线长的概念.
2、掌握切线长定理并会运用它解决有关问题.
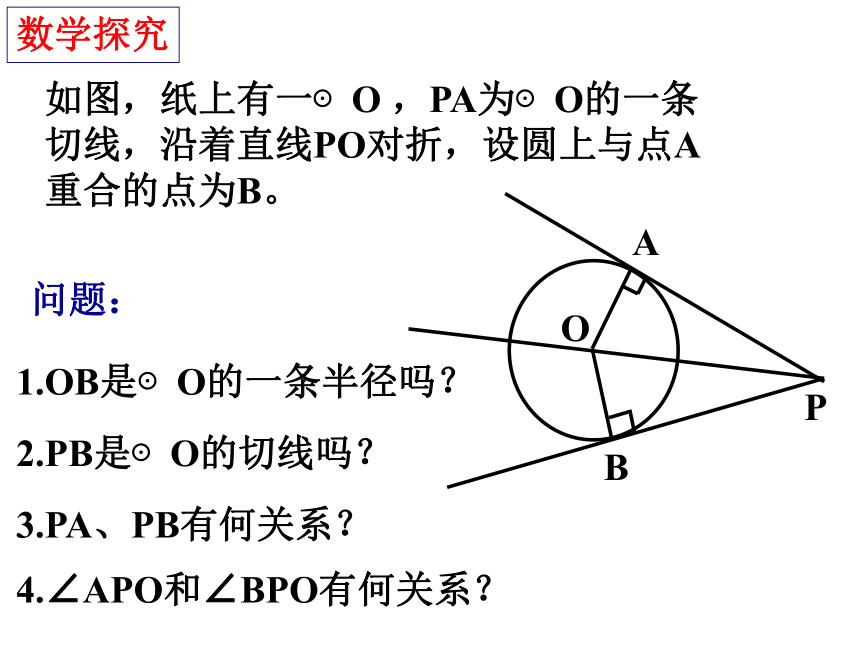
如图,纸上有一⊙O ,PA为⊙O的一条
切线,沿着直线PO对折,设圆上与点A
重合的点为B。
1.OB是⊙O的一条半径吗?
2.PB是⊙O的切线吗?
3.PA、PB有何关系?
4.∠APO和∠BPO有何关系?
数学探究
P
A
O
B
问题:
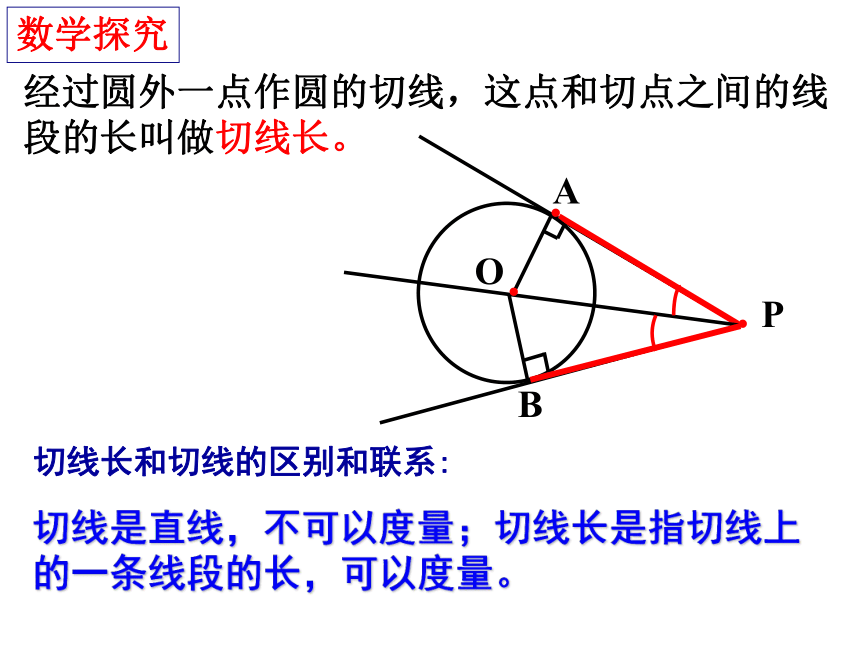
经过圆外一点作圆的切线,这点和切点之间的线段的长叫做切线长。
数学探究
O
B
P
·
·
A
·
切线长和切线的区别和联系:
切线是直线,不可以度量;切线长是指切线上的一条线段的长,可以度量。
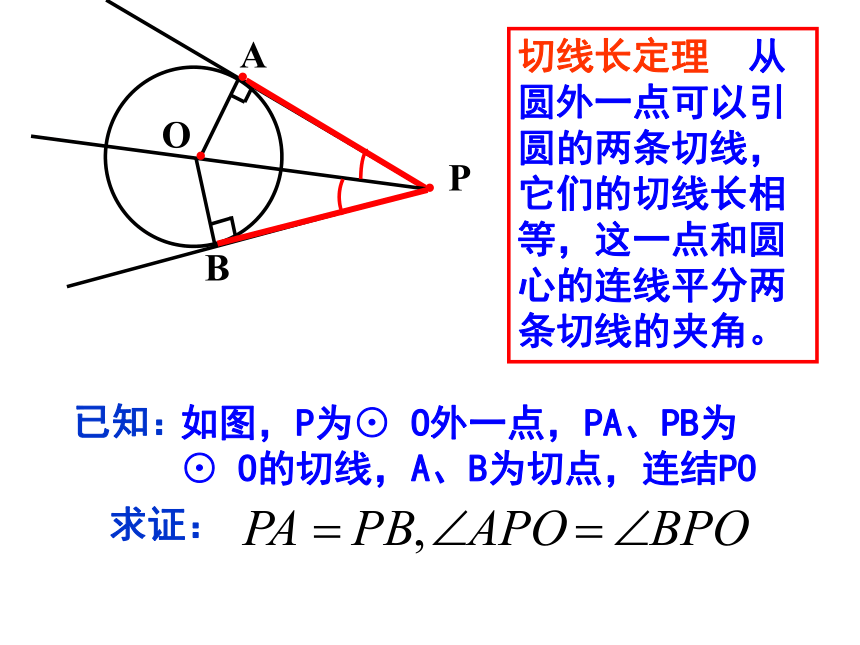
已知:
求证:
如图,P为⊙ O外一点,PA、PB为⊙ O的切线,A、B为切点,连结PO
切线长定理 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。
O
B
P
·
·
A
·
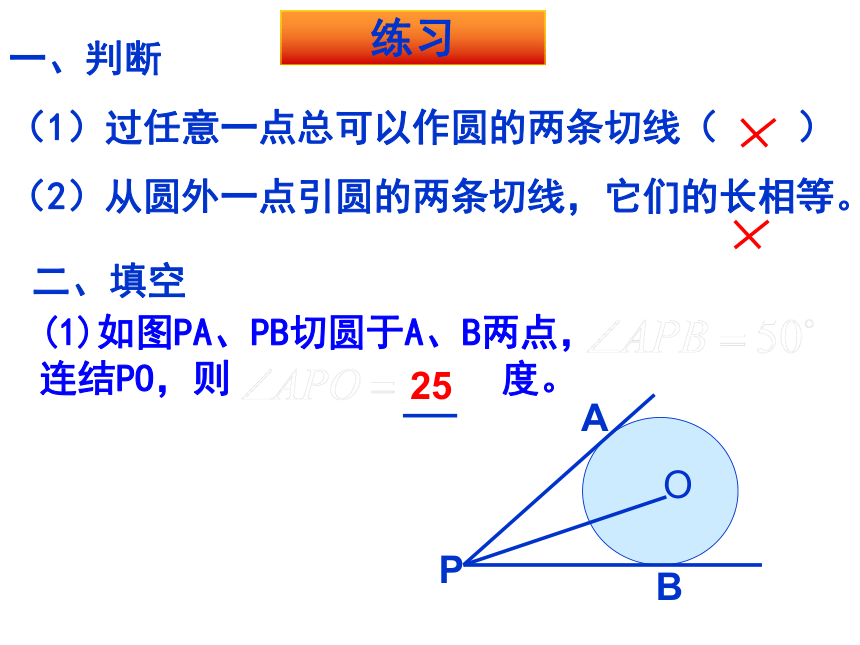
一、判断
(1)过任意一点总可以作圆的两条切线( )
(2)从圆外一点引圆的两条切线,它们的长相等。
练习
(1)如图PA、PB切圆于A、B两点, 连结PO,则 度。
P
B
O
A
二、填空
25
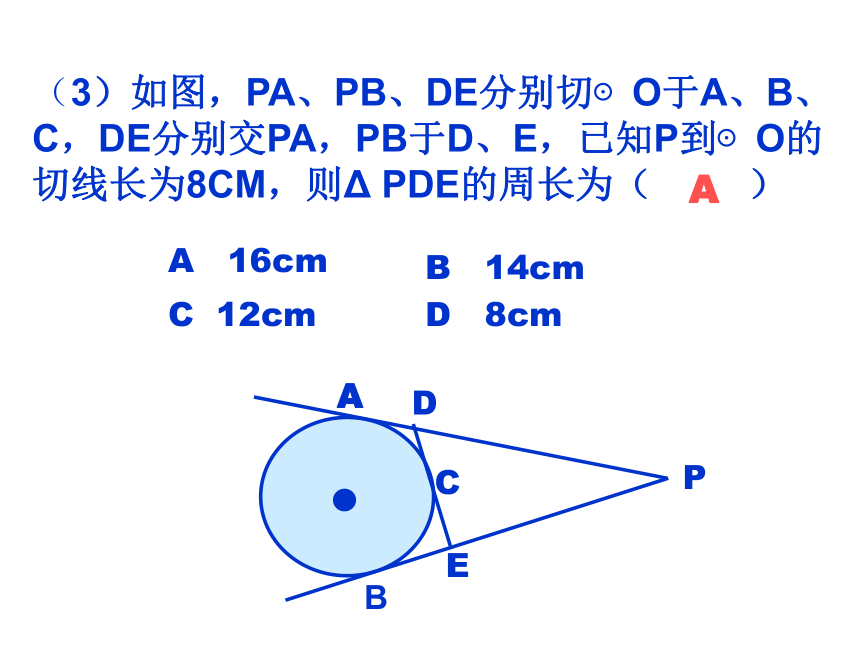
(3)如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则Δ PDE的周长为( )
A
A 16cm
D 8cm
C 12cm
B 14cm
D
C
B
E
A
P
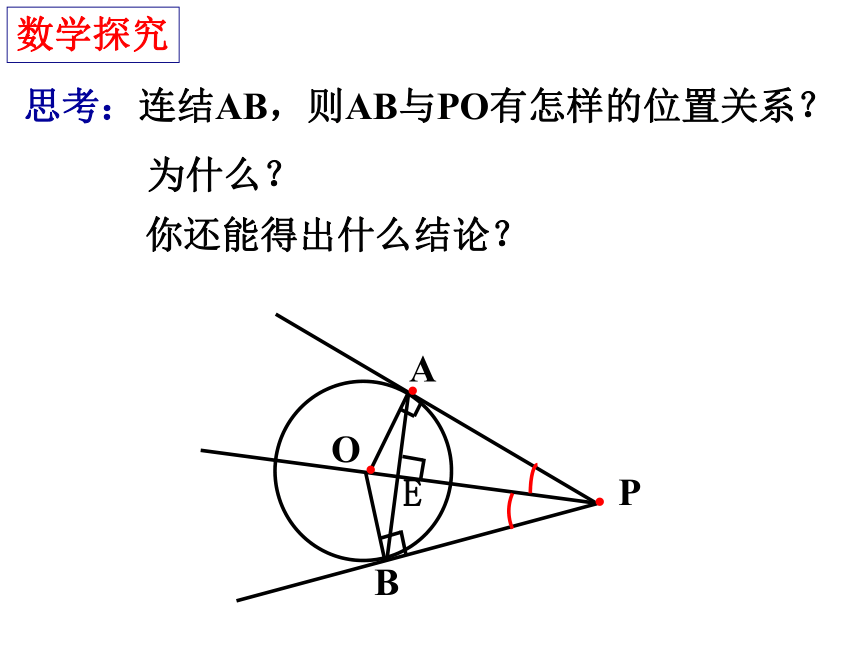
数学探究
O
B
P
·
·
A
·
思考:连结AB,则AB与PO有怎样的位置关系?
为什么?
你还能得出什么结论?
E
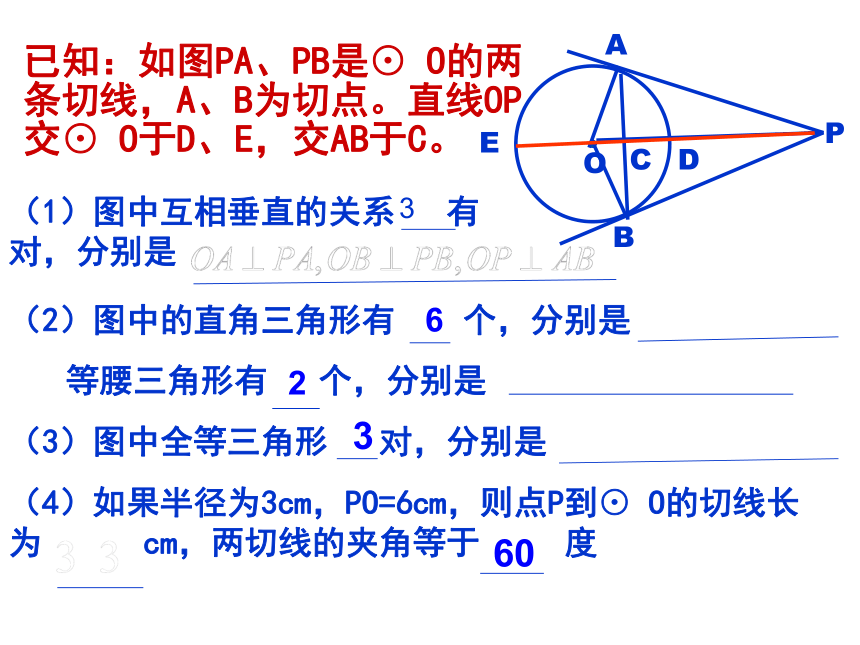
已知:如图PA、PB是⊙ O的两条切线,A、B为切点。直线OP交⊙ O于D、E,交AB于C。
O
P
A
B
C
D
E
(1)图中互相垂直的关系 有 对,分别是
(2)图中的直角三角形有 个,分别是
等腰三角形有 个,分别是
(3)图中全等三角形 对,分别是
(4)如果半径为3cm,PO=6cm,则点P到⊙ O的切线长为 cm,两切线的夹角等于 度
3
6
2
3
60
O
P
A
B
C
D
E
(5)如果PA=4cm,PD=2cm,试求半径OA的长。
x
即:
解得: x=
3cm
半径OA的长为3cm
例、如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30°.
(1)求∠APB的度数;
(2)当OA=3时,求AP的长.
P
B
A
O
1、如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形的周长为( )
(A)50 (B) 52 (C)54 (D) 56
D
A
B
C
当堂检测
(2)观察OP与BC的位置关系,并给予证明。
(1)若OA=3cm, ∠APB=60°,则PA=______.
P
A
B
C
O
M
2.如图,AC为⊙O的直径,PA、PB分别切⊙O于点A、B,OP交⊙O于点M,连结BC。
通过这节课的学习:
我学会了……
我还感到疑惑的是……
学习目标:
1、理解切线长的概念.
2、掌握切线长定理并会运用它解决有关问题.
回顾反思
2.切线长定理
O
B
P
·
·
A
·
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。
从圆外一点引圆的切线,这个点与切点间的线段的长称为切线长。
1.切线长:
1.已知:如图,P为⊙O外一点,PA,PB为⊙O的切线,A和B是切点,BC是直径。∠C=50 ,
①求∠APB的度数
②求证:AC∥OP。
A
B
O
C
P
提高题
A
O
B
C
2.如图,一个圆球放置在V形架中。图2是它的平面示意图,CA和CB都是⊙O的切线,切点分别是A、B。如果⊙O的半径为 cm,且AB=6cm,求∠ACB。
3、以正方形ABCD的一边BC为直径的半圆上有一个动点K,过点K作半圆的切线EF,EF分别交AB、CD于点E、F,试问:四边形AEFD的周长是否会因K点的变动而变化?为什么?
A
B
D
C
K
E
F
4、如图,在梯形ABCD中,AD//BC,AB⊥BC,以AB为直径的⊙O与DC相切于E.已知AB=8,边BC比AD大6,
求边AD、BC的长。
A
B
D
C
E
O
5.思考:当切点F在弧AB上运动时,问△PED的周长、∠DOE的度数是否发生变化,请说明理由。
F
O
E
D
P
B
A
切线长定理
学习目标:
1、理解切线长的概念.
2、掌握切线长定理并会运用它解决有关问题.
如图,纸上有一⊙O ,PA为⊙O的一条
切线,沿着直线PO对折,设圆上与点A
重合的点为B。
1.OB是⊙O的一条半径吗?
2.PB是⊙O的切线吗?
3.PA、PB有何关系?
4.∠APO和∠BPO有何关系?
数学探究
P
A
O
B
问题:
经过圆外一点作圆的切线,这点和切点之间的线段的长叫做切线长。
数学探究
O
B
P
·
·
A
·
切线长和切线的区别和联系:
切线是直线,不可以度量;切线长是指切线上的一条线段的长,可以度量。
已知:
求证:
如图,P为⊙ O外一点,PA、PB为⊙ O的切线,A、B为切点,连结PO
切线长定理 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。
O
B
P
·
·
A
·
一、判断
(1)过任意一点总可以作圆的两条切线( )
(2)从圆外一点引圆的两条切线,它们的长相等。
练习
(1)如图PA、PB切圆于A、B两点, 连结PO,则 度。
P
B
O
A
二、填空
25
(3)如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则Δ PDE的周长为( )
A
A 16cm
D 8cm
C 12cm
B 14cm
D
C
B
E
A
P
数学探究
O
B
P
·
·
A
·
思考:连结AB,则AB与PO有怎样的位置关系?
为什么?
你还能得出什么结论?
E
已知:如图PA、PB是⊙ O的两条切线,A、B为切点。直线OP交⊙ O于D、E,交AB于C。
O
P
A
B
C
D
E
(1)图中互相垂直的关系 有 对,分别是
(2)图中的直角三角形有 个,分别是
等腰三角形有 个,分别是
(3)图中全等三角形 对,分别是
(4)如果半径为3cm,PO=6cm,则点P到⊙ O的切线长为 cm,两切线的夹角等于 度
3
6
2
3
60
O
P
A
B
C
D
E
(5)如果PA=4cm,PD=2cm,试求半径OA的长。
x
即:
解得: x=
3cm
半径OA的长为3cm
例、如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30°.
(1)求∠APB的度数;
(2)当OA=3时,求AP的长.
P
B
A
O
1、如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形的周长为( )
(A)50 (B) 52 (C)54 (D) 56
D
A
B
C
当堂检测
(2)观察OP与BC的位置关系,并给予证明。
(1)若OA=3cm, ∠APB=60°,则PA=______.
P
A
B
C
O
M
2.如图,AC为⊙O的直径,PA、PB分别切⊙O于点A、B,OP交⊙O于点M,连结BC。
通过这节课的学习:
我学会了……
我还感到疑惑的是……
学习目标:
1、理解切线长的概念.
2、掌握切线长定理并会运用它解决有关问题.
回顾反思
2.切线长定理
O
B
P
·
·
A
·
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。
从圆外一点引圆的切线,这个点与切点间的线段的长称为切线长。
1.切线长:
1.已知:如图,P为⊙O外一点,PA,PB为⊙O的切线,A和B是切点,BC是直径。∠C=50 ,
①求∠APB的度数
②求证:AC∥OP。
A
B
O
C
P
提高题
A
O
B
C
2.如图,一个圆球放置在V形架中。图2是它的平面示意图,CA和CB都是⊙O的切线,切点分别是A、B。如果⊙O的半径为 cm,且AB=6cm,求∠ACB。
3、以正方形ABCD的一边BC为直径的半圆上有一个动点K,过点K作半圆的切线EF,EF分别交AB、CD于点E、F,试问:四边形AEFD的周长是否会因K点的变动而变化?为什么?
A
B
D
C
K
E
F
4、如图,在梯形ABCD中,AD//BC,AB⊥BC,以AB为直径的⊙O与DC相切于E.已知AB=8,边BC比AD大6,
求边AD、BC的长。
A
B
D
C
E
O
5.思考:当切点F在弧AB上运动时,问△PED的周长、∠DOE的度数是否发生变化,请说明理由。
F
O
E
D
P
B
A
