湘教版数学九年级下册第三章3.2 圆锥的侧面积和全面积 课件 (共27张PPT)
文档属性
| 名称 | 湘教版数学九年级下册第三章3.2 圆锥的侧面积和全面积 课件 (共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1003.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
1、弧长计算公式
2、扇形面积计算公式
复习引入
圆锥的侧面展开图
生活中的圆锥
学习目标:
1.掌握圆锥及相关概念
2.掌握圆锥的侧面展开图与圆锥的关系
3.会运用圆锥的侧面积计算公式计算有关问题
自学指导:
1、请同学们仔细阅读P102“观察”部分,熟记圆锥,高,母线的概念;熟知高、母线、半径三者之间的关系;
2、看P103上段文字,学会将圆锥侧面展开,掌握侧面展开图的半径、弧长与圆锥的关系;
3、看例题2,学会计算圆锥侧面展开图的面积。
(5分钟)
1、 填空:根据下列条件求值(其中r、h、a 分别是圆锥的底面半径、高线、母线长)。
(1) h =3, r=4 则 a =_______
(2) a = 2,r=1 则 h =_______
(3) a= 10, h = 8 则r =_______
5
6
自学检测
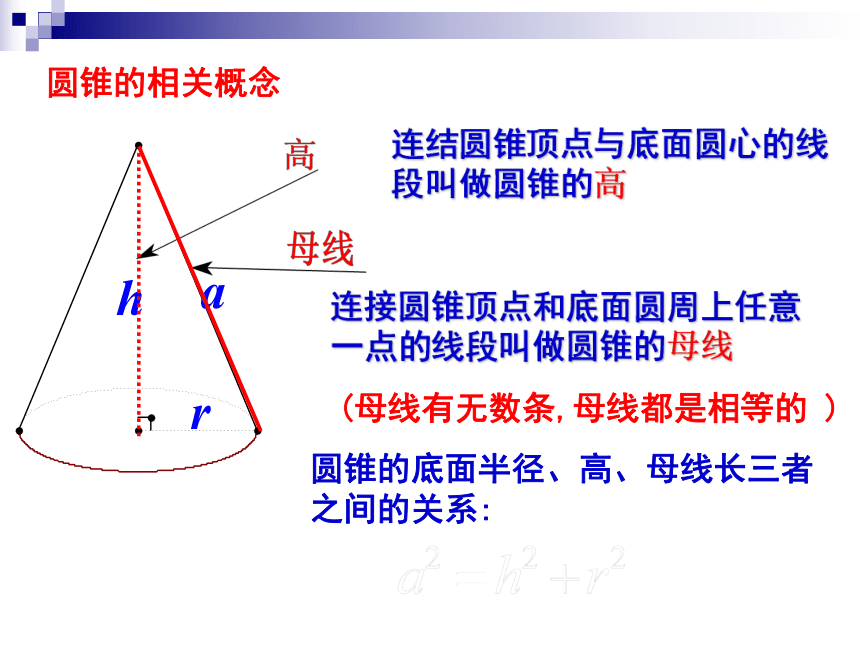
圆锥的相关概念
连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线
连结圆锥顶点与底面圆心的线段叫做圆锥的高
圆锥的底面半径、高、母线长三者之间的关系:
(母线有无数条,母线都是相等的 )
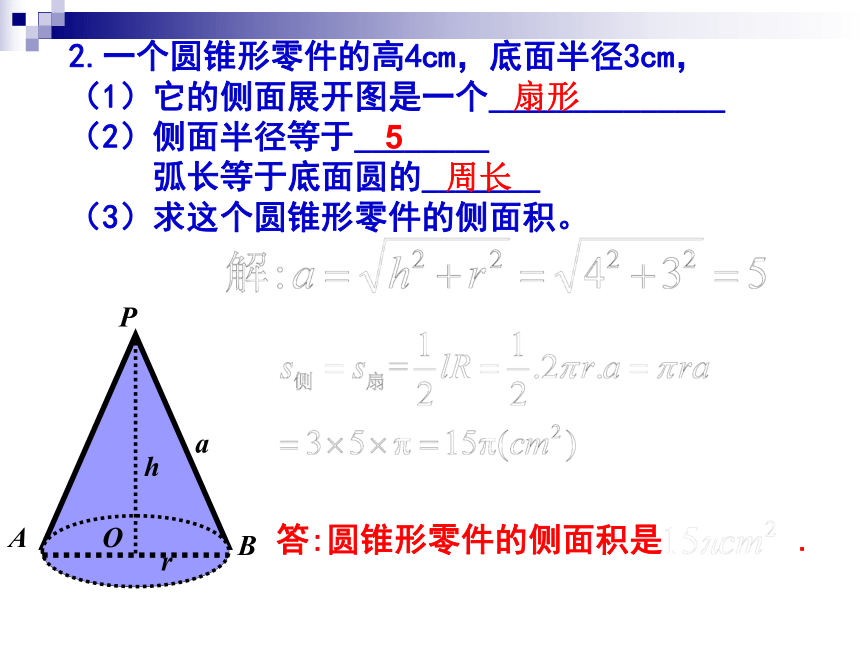
2.一个圆锥形零件的高4cm,底面半径3cm,
(1)它的侧面展开图是一个______________
(2)侧面半径等于________
弧长等于底面圆的_______
(3)求这个圆锥形零件的侧面积。
O
P
A
B
r
h
a
答:圆锥形零件的侧面积是 .
扇形
5
周长
圆锥与侧面展开图之间的主要关系
沿着圆锥的母线,把一个圆锥的侧面展开,得到
一个扇形。
1、这个扇形的半径与圆锥中的哪一条线段相等?
2、这个扇形的弧长与底面的周长有什么关系?
3、圆锥的侧面积和这个扇形的面积有什么关系
1.圆锥的母线长=扇形的半径
2.圆锥的底面周长=扇形的弧长
圆锥与侧面展开图之间的主要关系:
n
R
a = R
C = l
3.圆锥的侧面积=扇形的面积
圆锥的侧面积
圆锥的侧面积=扇形的面积
n
公式一:
R
一展身手
1、一个圆锥形零件的高3cm,底面半径4cm,求这个圆锥形零件的侧面积和全面积。
O
P
A
B
r
h
a
答:圆锥形零件的侧面积是 .
圆锥的全面积
n
圆锥的全面积=圆锥的侧面积+底面积.
2、已知某扇形的半径3cm,圆心角是120°,把这个扇形围成圆锥,求它的底面圆半径和高。
n
挑战自我
如图,圆锥的底面半径为1,母线长为6,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬行一圈再回到点B,问它爬行的最短路线是多少
A
B
C
6
1
B’
解:设圆锥的侧面展开图为扇形ABB’, ∠BAB’=n°
∴ △ABB’是等边三角形
答:蚂蚁爬行的最短路线为6.
解得: n=60
连接BB’,即为蚂蚁爬行的最短路线
∴ BB’=AB=6
五、小结升华
1、本节课所学:“一个图形、三个关系、两个公式”,理解关系,牢记公式;
2、立体图形的处理方式--转化为平面几何图形
圆锥与侧面展开图之间的主要关系:
1、圆锥的母线长=扇形的半径
2、圆锥的底面周长=扇形的弧长
3、圆锥的侧面积=扇形的面积
(a = R)
(C = l)
n
当堂训练
1、已知圆锥的底面半径为4,母线长为6,则它的侧面积为_________.
2
2、已知圆锥底面圆的半径为2cm,高为 ,求这个圆锥的全面积。
3.圆锥的底面半径为3cm,母线长为6cm,则这个圆锥侧面展开图扇形的圆心角是多少?
3、 填空、根据下列条件求值 .
(1) a=2, r=1 则n =_______
(2) a=9, r=3 则n =_______
(3) n=90°,a=4 则r =_______
(4) n=60°,r= 3 则a =_______
n
180°
120°
1
18
n
圆锥的侧面积
公式二:
n
圆锥的侧面积
公式二:
3.如图所示的扇形中,半径R=10,圆心角θ=144°用这个扇形围成一个圆锥的侧面.
(1)求这个圆锥的底面半径r;
(2)求这个圆锥的高(精确到0.1)
2.圆锥的底面直径是80cm,母线长90cm,它的侧面展开图的圆心角是_________;圆锥的侧面积为_________;底面积_________;全面积是_________。
3.用一个圆心角为120°,半径为4的扇形做一个圆锥的侧面,这个圆锥的底面半径是____。
选做题
1.圆锥的侧面积是底面积的2倍,这个圆锥的侧面展开图扇形的圆心角是 ____ 。
2 .一个扇形的半径为30cm,圆心角为120度,用它做成一个圆锥的侧面,那么这个圆锥的底面半径为_____ 。
3.圆锥的底面半径为10cm,母线长40cm,底面圆周上的蚂蚁绕侧面一周的最短的长度是_______。
10cm
180o
4.如图,已知RtΔABC中,∠ACB=90°,AC= 4,BC=3,
以AB边所在的直线为轴,将ΔABC旋转一周,则所得几何体的表面积是多少?
5.如图(1),在正方形铁皮上剪下一个圆形和扇形,使之恰好围成图(2)所示的一个圆锥模型.设圆的半径为r,扇形半径为R,则圆的半径与扇形半径之间的关系为____.
问题2.圆柱的侧面积怎样计算?
思考:1.将圆柱的侧面展开是什么图形?
圆柱的底面圆周长就是
展开图中的矩形的长
圆柱的母线长就是展开图中的矩形的宽
母线
答:圆柱的侧面展开图形是矩形.
答:计算圆柱的则面积只需计算一个矩形的面积.
S 侧面积
= 底面圆周长×母线长
S全面积
= 侧面积+ 2个底面积
圆柱
6.蒙古包可以近似地看成由圆锥和圆柱组成的.如果想用毛毡搭建20个底面积为35 m2,高为3.5 m,外围高1.5 m的蒙古包,至少需要多少m2的毛毡 (结果精确到1 m2).
r
r
h1
h2
依题意,下部圆柱的底面积35m2,高为1.5m;
解:如图是一个蒙古包的示意图
上部圆锥的高为3.5-1.5=2 m;
≈3.34 (m)
圆柱底面圆半径r=
π
35
(m)
侧面积为:
2π×3.34×1.5
≈31.45 (m2)
圆锥的母线长为
3.342+22
≈3.85 (m)
≈20.98 (m)
2π×3.34
侧面展开积扇形的弧长为:
≈40.81 (m2)
圆锥侧面积为:
×3.89×20.98
1
2
因此,搭建20个这样的蒙古包至少需要毛毡:
20× (31.45+40.81)≈1445(m2)
1、弧长计算公式
2、扇形面积计算公式
复习引入
圆锥的侧面展开图
生活中的圆锥
学习目标:
1.掌握圆锥及相关概念
2.掌握圆锥的侧面展开图与圆锥的关系
3.会运用圆锥的侧面积计算公式计算有关问题
自学指导:
1、请同学们仔细阅读P102“观察”部分,熟记圆锥,高,母线的概念;熟知高、母线、半径三者之间的关系;
2、看P103上段文字,学会将圆锥侧面展开,掌握侧面展开图的半径、弧长与圆锥的关系;
3、看例题2,学会计算圆锥侧面展开图的面积。
(5分钟)
1、 填空:根据下列条件求值(其中r、h、a 分别是圆锥的底面半径、高线、母线长)。
(1) h =3, r=4 则 a =_______
(2) a = 2,r=1 则 h =_______
(3) a= 10, h = 8 则r =_______
5
6
自学检测
圆锥的相关概念
连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线
连结圆锥顶点与底面圆心的线段叫做圆锥的高
圆锥的底面半径、高、母线长三者之间的关系:
(母线有无数条,母线都是相等的 )
2.一个圆锥形零件的高4cm,底面半径3cm,
(1)它的侧面展开图是一个______________
(2)侧面半径等于________
弧长等于底面圆的_______
(3)求这个圆锥形零件的侧面积。
O
P
A
B
r
h
a
答:圆锥形零件的侧面积是 .
扇形
5
周长
圆锥与侧面展开图之间的主要关系
沿着圆锥的母线,把一个圆锥的侧面展开,得到
一个扇形。
1、这个扇形的半径与圆锥中的哪一条线段相等?
2、这个扇形的弧长与底面的周长有什么关系?
3、圆锥的侧面积和这个扇形的面积有什么关系
1.圆锥的母线长=扇形的半径
2.圆锥的底面周长=扇形的弧长
圆锥与侧面展开图之间的主要关系:
n
R
a = R
C = l
3.圆锥的侧面积=扇形的面积
圆锥的侧面积
圆锥的侧面积=扇形的面积
n
公式一:
R
一展身手
1、一个圆锥形零件的高3cm,底面半径4cm,求这个圆锥形零件的侧面积和全面积。
O
P
A
B
r
h
a
答:圆锥形零件的侧面积是 .
圆锥的全面积
n
圆锥的全面积=圆锥的侧面积+底面积.
2、已知某扇形的半径3cm,圆心角是120°,把这个扇形围成圆锥,求它的底面圆半径和高。
n
挑战自我
如图,圆锥的底面半径为1,母线长为6,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬行一圈再回到点B,问它爬行的最短路线是多少
A
B
C
6
1
B’
解:设圆锥的侧面展开图为扇形ABB’, ∠BAB’=n°
∴ △ABB’是等边三角形
答:蚂蚁爬行的最短路线为6.
解得: n=60
连接BB’,即为蚂蚁爬行的最短路线
∴ BB’=AB=6
五、小结升华
1、本节课所学:“一个图形、三个关系、两个公式”,理解关系,牢记公式;
2、立体图形的处理方式--转化为平面几何图形
圆锥与侧面展开图之间的主要关系:
1、圆锥的母线长=扇形的半径
2、圆锥的底面周长=扇形的弧长
3、圆锥的侧面积=扇形的面积
(a = R)
(C = l)
n
当堂训练
1、已知圆锥的底面半径为4,母线长为6,则它的侧面积为_________.
2
2、已知圆锥底面圆的半径为2cm,高为 ,求这个圆锥的全面积。
3.圆锥的底面半径为3cm,母线长为6cm,则这个圆锥侧面展开图扇形的圆心角是多少?
3、 填空、根据下列条件求值 .
(1) a=2, r=1 则n =_______
(2) a=9, r=3 则n =_______
(3) n=90°,a=4 则r =_______
(4) n=60°,r= 3 则a =_______
n
180°
120°
1
18
n
圆锥的侧面积
公式二:
n
圆锥的侧面积
公式二:
3.如图所示的扇形中,半径R=10,圆心角θ=144°用这个扇形围成一个圆锥的侧面.
(1)求这个圆锥的底面半径r;
(2)求这个圆锥的高(精确到0.1)
2.圆锥的底面直径是80cm,母线长90cm,它的侧面展开图的圆心角是_________;圆锥的侧面积为_________;底面积_________;全面积是_________。
3.用一个圆心角为120°,半径为4的扇形做一个圆锥的侧面,这个圆锥的底面半径是____。
选做题
1.圆锥的侧面积是底面积的2倍,这个圆锥的侧面展开图扇形的圆心角是 ____ 。
2 .一个扇形的半径为30cm,圆心角为120度,用它做成一个圆锥的侧面,那么这个圆锥的底面半径为_____ 。
3.圆锥的底面半径为10cm,母线长40cm,底面圆周上的蚂蚁绕侧面一周的最短的长度是_______。
10cm
180o
4.如图,已知RtΔABC中,∠ACB=90°,AC= 4,BC=3,
以AB边所在的直线为轴,将ΔABC旋转一周,则所得几何体的表面积是多少?
5.如图(1),在正方形铁皮上剪下一个圆形和扇形,使之恰好围成图(2)所示的一个圆锥模型.设圆的半径为r,扇形半径为R,则圆的半径与扇形半径之间的关系为____.
问题2.圆柱的侧面积怎样计算?
思考:1.将圆柱的侧面展开是什么图形?
圆柱的底面圆周长就是
展开图中的矩形的长
圆柱的母线长就是展开图中的矩形的宽
母线
答:圆柱的侧面展开图形是矩形.
答:计算圆柱的则面积只需计算一个矩形的面积.
S 侧面积
= 底面圆周长×母线长
S全面积
= 侧面积+ 2个底面积
圆柱
6.蒙古包可以近似地看成由圆锥和圆柱组成的.如果想用毛毡搭建20个底面积为35 m2,高为3.5 m,外围高1.5 m的蒙古包,至少需要多少m2的毛毡 (结果精确到1 m2).
r
r
h1
h2
依题意,下部圆柱的底面积35m2,高为1.5m;
解:如图是一个蒙古包的示意图
上部圆锥的高为3.5-1.5=2 m;
≈3.34 (m)
圆柱底面圆半径r=
π
35
(m)
侧面积为:
2π×3.34×1.5
≈31.45 (m2)
圆锥的母线长为
3.342+22
≈3.85 (m)
≈20.98 (m)
2π×3.34
侧面展开积扇形的弧长为:
≈40.81 (m2)
圆锥侧面积为:
×3.89×20.98
1
2
因此,搭建20个这样的蒙古包至少需要毛毡:
20× (31.45+40.81)≈1445(m2)
