沪科版数学七年级下册 第8章 整式乘法和因式分解 单元测试题(word解析版)
文档属性
| 名称 | 沪科版数学七年级下册 第8章 整式乘法和因式分解 单元测试题(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 540.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 16:34:48 | ||
图片预览




文档简介
第8章 整式乘法和因式分解 单元测试
一、单选题:本题共10个小题,每小题2分,共20分。在每小题给出的四个选项中只有一项是符合题目要求的。
1.(2022·全国·七年级期末)如果xm=2,xn=,那么xm+n的值为( )
A.2 B.8 C. D.2
(2021·广东番禺·七年级期末)下列运算中正确的是( ).
A. B. C. D.
3.(2022·上海金山·七年级期中)下列计算正确的是( )
A. B.
C. D.
4.(2022·湖北潜江·七年级期末)如果,那么代数式的值为( )
A. B. C.6 D.8
5.(2022·湖南·七年级单元测试)已知x+y=4 ,xy=3 ,则x2+ y2的值为( )
A.22 B.16 C.10 D.4
6.(2021·北京·七年级期中)如图,由4个全等的小长方形与1个小正方形密铺成正方形图案,该图案的面积为49,小正方形的面积为4,若分别用,表示小长方形的长和宽,则下列关系式中不正确的是( )
A. B. C. D.
7.(2022·广东中山·七年级期末)如图,两个正方形的边长分别为a、b,若,,则阴影部分的面积是( )
A.40 B. C.20 D.23
(2022·全国·七年级单元测试)下列各式从左到右的变形中,是因式分解的为( ).
A. B.
C. D.
9.(2022·山西·七年级期末)英国曼彻斯特大学的两位科学家因为成功地从石墨中分离出石墨烯,荣获了诺贝尔物理学奖.石墨烯是目前世上最薄却也是最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.00000034毫米,将数0.00000034用科学记数法表示为( )
A. B. C. D.
10.(2021·全国·七年级单元测试)如图,在边长为的正方形中挖掉一个边长为的小正方形,把余下的部分剪成一个矩形,通过计算两个图形(阴影部分)的面积,验证了一个等式是( )
A. B.
C. D.
二、填空题:本题共8个小题,每题3分,共24分。
11.(2021·北京·七年级期中)若,,则的值为 __.
12.(2021·广东茂南·七年级期末)若单项式与b的和仍是单项式,则的值是________.
13.(2021·全国·七年级单元测试)若长方形的面积是6a3+5ab+3a,长为3a,则它的宽为____.
14.(2021·全国·七年级单元测试)旧知回顾:在七年级学方根”时,我们会直接开方解形如的方程(解为).解题运用:方程解为_________.
15.(2022·福建·厦门外国语学校七年级期末)如图,边长为(m+3)的正方形纸片剪出一个边长为m的正方形之后,剩余部分又剪拼成一个长方形(不重叠无缝隙),则拼成的长方形的周长是_________.
16.(2021·山东莱西·七年级期中)已知ab=2,=,则多项式a3b+2a2b2+ab3的值为______.
17.(2021·江苏·无锡市天一实验学校七年级期中)熔喷布,俗称口罩的“心脏”,是口罩中间的过滤层,能过滤细菌,阻止病菌传播.经测量,医用外科口罩的熔喷布厚度约为0.000156米,将0.000156用科学记数法表示应为__________.
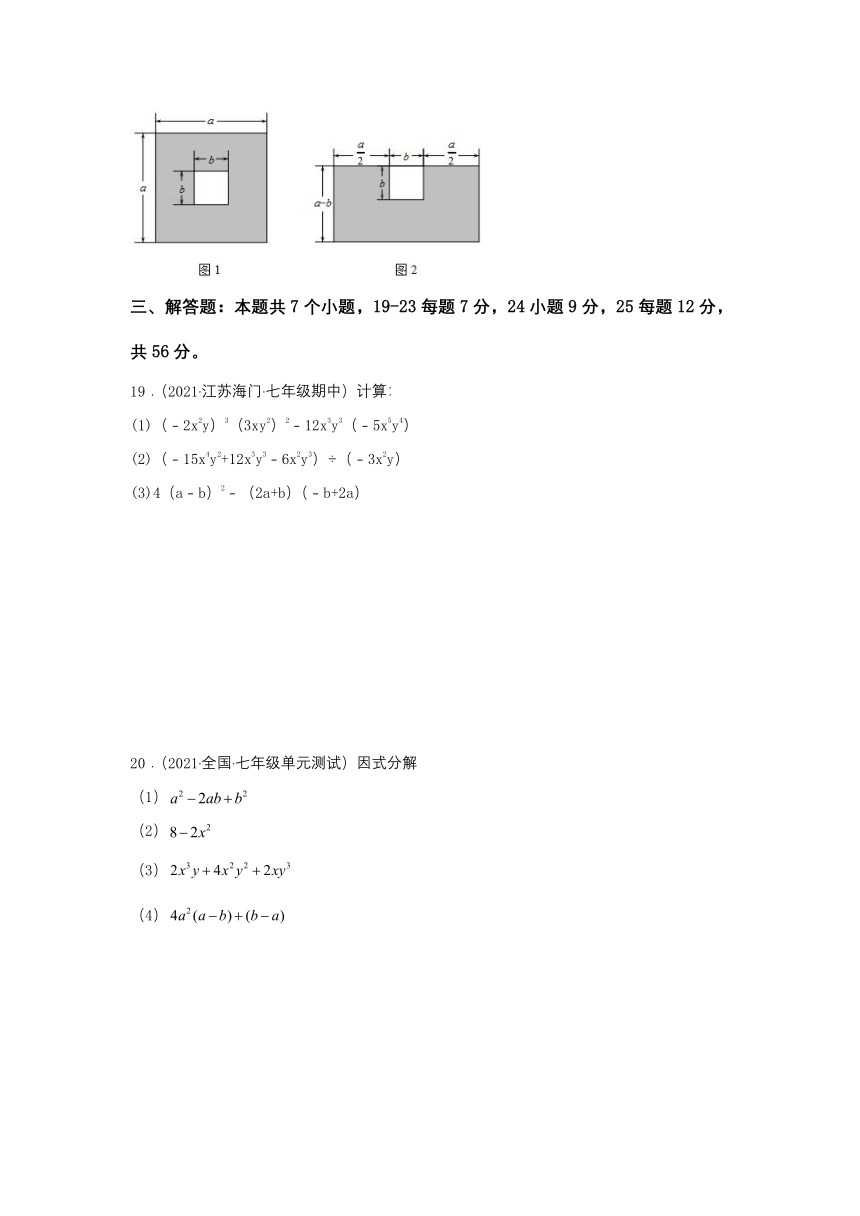
18.(2021·北京·七年级期末)某中学要举行校庆活动,现计划在教学楼之间的广场上搭建舞台.已知广场中心有一座边长为的正方形的花坛.学生会提出两个方案:方案一:如图1,围绕花坛搭建外围为正方形的“回”字形舞台(阴影部分),舞台的面积记为;方案二:如图2,在花坛的三面搭建“凹”字形舞台(阴影部分),舞台的面积记为;具体数据如图所示,则______.(填“”,“”或“”)
三、解答题:本题共7个小题,19-23每题7分,24小题9分,25每题12分,共56分。
19.(2021·江苏海门·七年级期中)计算:
(1)(﹣2x2y)3(3xy2)2﹣12x3y3(﹣5x5y4)
(2)(﹣15x4y2+12x3y3﹣6x2y3)÷(﹣3x2y)
(3)4(a﹣b)2﹣(2a+b)(﹣b+2a)
20.(2021·全国·七年级单元测试)因式分解
(1)
(2)
(3)
(4)
21.(2022·吉林市第五中学七年级期末)如图1,有甲、乙、丙三种纸片,其中甲是边长为a的正方形,乙是长为a,宽为b的长方形,丙是边长为b的正方形(a>b).
(1)如图2,用甲、丙纸片各1张,乙纸片2张,可以紧密拼接成一个大正方形,请根据图形的面积写出一个乘法公式 ;
(2)若要用这三种纸片紧密拼接成一个边长为(2a+b)大正方形,则需要取甲、乙、丙纸片各多少张.
22.(2021·全国·七年级单元测试)阅读下列材料:
①关于x的方程方程两边同时乘以得:,即,故,所以.
②;.
根据以上材料,解答下列问题:
(1),则______ ;______ ;______ ;
(2),求的值.
23.(2022·福建·泉州五中七年级期末)对于一个图形,通过不同的方法计算图形的面积,就可以得到一个数学等式.
(1)模拟练习:如图,写出一个我们熟悉的数学公式: ;
(2)解决问题:如果,求的值;
(3)类比探究:如果一个长方形的长和宽分别为和,且,求这个长方形的面积.
24.(2021·上海浦东新·七年级期中)数学课上,王老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b,宽为a的长方形.并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积:
方法1: ;
方法2: ;
(2)观察图2,请你写出代数式:(a+b)2,a2+b2,ab之间的等量关系 ;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,(a﹣b)2=13,求ab的值;
②已知(2021﹣a)2+(a﹣2022)2=5,求(2021﹣a)(a﹣2022)的值.
25.(2022·广东乐昌·七年级期末)教科书中这样写道:“我们把多项式及叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.能解决一些与非负数有关的问题或求代数式最大值,最小值等.
例如:分解因式.
原式
例如.求代数式的最小值.
原式
.
可知当时,有最小值,最小值是-3.
(1)分解因式:__________.
(2)试说明:、取任何实数时,多项式的值总为正数.
(3)当,为何值时,多项式有最小值,并求出这个最小值.
第8章 整式乘法和因式分解 单元测试
单选题:本题共10个小题,每小题2分,共20分。在每小题给出的四个选项中只有一项是符合题目要求的。
1.(2022·全国·七年级期末)如果xm=2,xn=,那么xm+n的值为( )
A.2 B.8 C. D.2
【答案】C
【分析】根据同底数幂的乘法进行运算即可.
【详解】解:如果xm=2,xn=,
那么xm+n=xm×xn=2×=.
故选:C.
【点睛】本题考查了同底数幂的乘法,解题的关键是熟练掌握同底数幂的乘法公式.
(2021·广东番禺·七年级期末)下列运算中正确的是( ).
A. B. C. D.
【答案】D
【分析】根据同底数相乘,幂的乘方,积的乘方,同底数相除法则,逐项判断即可求解.
【详解】解:A、,故本选项错误,不符合题意;B、,故本选项错误,不符合题意;
C、,故本选项错误,不符合题意;D、,故本选项正确,符合题意;
故选:D
【点睛】本题主要考查了同底数相乘,幂的乘方,积的乘方,同底数相除法则,熟练掌握同底数相乘,幂的乘方,积的乘方,同底数相除法则是解题的关键.
3.(2022·上海金山·七年级期中)下列计算正确的是( )
A. B.
C. D.
【答案】B
【分析】利用合并同类项的法则,单项式乘单项式的法则,多项式乘多项式的法则对各项进行运算即可.
【详解】解:A、2x+3x=5x,故A不符合题意;B、2a2 3a=6a3,故B符合题意;C、(x-2)(x+3)=x2+x-6,故C不符合题意;D、2x3 3x2=6x5,故D不符合题意;
故选:B.
【点睛】本题主要考查合并同类项,单项式乘单项式,多项式乘多项式,解答的关键是对相应的运算法则的掌握.
4.(2022·湖北潜江·七年级期末)如果,那么代数式的值为( )
A. B. C.6 D.8
【答案】D
【分析】先将原式根据单项式乘以多项式法则及完全平方公式法则去括号,合并同类项,再将式子的值代入计算求出答案.
【详解】解:∵
=
=
=
∵,
∴原式==8,
故选:D.
【点睛】此题考查了已知式子的值求代数式的值,正确掌握整式的混合运算法则是解题的关键.
5.(2022·湖南·七年级单元测试)已知x+y=4 ,xy=3 ,则x2+ y2的值为( )
A.22 B.16 C.10 D.4
【答案】C
【分析】根据完全平方公式变形,整体代入求值即可.
【详解】解:.
故选择C.
【点睛】本题考查式子的值,求代数式的值,掌握完全平方公式变形的方法是解题关键.
6.(2021·北京·七年级期中)如图,由4个全等的小长方形与1个小正方形密铺成正方形图案,该图案的面积为49,小正方形的面积为4,若分别用,表示小长方形的长和宽,则下列关系式中不正确的是( )
A. B. C. D.
【答案】C
【分析】根据完全平方公式及图形的特点找到长度关系即可依次判断.
【详解】解:、因为正方形图案的边长7,同时还可用来表示,故,正确;、由图象可知,即,正确;、由和,可得,,错误;、由,,可得,,所以,正确.
故选:.
【点睛】本题主要考查了完全平方公式的几何背景,解答本题需结合图形,利用等式的变形来解决问题.
7.(2022·广东中山·七年级期末)如图,两个正方形的边长分别为a、b,若,,则阴影部分的面积是( )
A.40 B. C.20 D.23
【答案】C
【分析】根据阴影部分面积等于2个正方形面积减去2个空白部分的三角形面积,进而根据完全平方公式的变形求解即可
【详解】解:阴影部分面积等于
∵,,
∴阴影部分面积等于
故答案为:C
【点睛】本题考查了完全平方公式变形求图形面积,掌握完全平方公式是解题的关键.
(2022·全国·七年级单元测试)下列各式从左到右的变形中,是因式分解的为( ).
A. B.
C. D.
【答案】B
【分析】根据因式分解的定义把一个多项式化成几个整式的积的形式,叫因式分解.然后对各选项逐个判断即可.
【详解】解:A、两因式之间用加号连结,是和的形式不是因式分解,故本选项不符合题意;B、是因式分解,故本选项符合题意;C、将积化为和差形式,是多项式乘法运算,不是因式分解,故本选项不符合题意;D、两因式之间用加号连结,是和的形式,不是因式分解,故本选项不符合题意;
故选:B.
【点睛】本题考查了因式分解的定义,能熟记因式分解的定义的内容是解此题的关键 .
9.(2022·山西·七年级期末)英国曼彻斯特大学的两位科学家因为成功地从石墨中分离出石墨烯,荣获了诺贝尔物理学奖.石墨烯是目前世上最薄却也是最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.00000034毫米,将数0.00000034用科学记数法表示为( )
A. B. C. D.
【答案】D
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10 n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【详解】解:0.00000034=,
故选:D.
【点睛】本题考查用科学记数法表示较小的数,一般形式为a×10 n,其中1≤a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
10.(2021·全国·七年级单元测试)如图,在边长为的正方形中挖掉一个边长为的小正方形,把余下的部分剪成一个矩形,通过计算两个图形(阴影部分)的面积,验证了一个等式是( )
A. B.
C. D.
【答案】A
【分析】左图中阴影部分的面积=a2 b2,右图中矩形面积=(a+b)(a b),根据二者面积相等,即可解答.
【详解】解:由题意可得:a2 b2=(a b)(a+b).
故选:A.
【点睛】此题主要考查了乘法的平方差公式,属于基础题型.
二、填空题:本题共8个小题,每题3分,共24分。
11.(2021·北京·七年级期中)若,,则的值为 __.
【答案】
【分析】逆向运用同底数幂的除法法则以及利用幂的乘方运算法则解答即可,同底数幂的除法法则:底数不变,指数相减;幂的乘方法则:底数不变,指数相乘.
【详解】解:,
,
解得,
,
.
故答案为:2.
【点睛】本题考查了同底数幂的除法以及幂的乘方,掌握幂的运算法则是解答本题的关键.
12.(2021·广东茂南·七年级期末)若单项式与b的和仍是单项式,则的值是________.
【答案】1
【分析】由题意知与是同类项,有,求出的值,然后代入求解即可.
【详解】解:由题意知与是同类项
∴
解得
∴
故答案为:1.
【点睛】本题考查了同类项,0指数幂.解题的关键在于正确的计算.
13.(2021·全国·七年级单元测试)若长方形的面积是6a3+5ab+3a,长为3a,则它的宽为____.
【答案】2a2+b+1
【分析】根据整式的除法即可求出答案.
【详解】解:(6a3+5ab+3a)÷3a
=2a2+b+1,
故答案为:2a2+b+1.
【点睛】本题考查整式的运算,解题的关键是熟练运用整式的除法法则,本题属于基础题型.
14.(2021·全国·七年级单元测试)旧知回顾:在七年级学方根”时,我们会直接开方解形如的方程(解为).解题运用:方程解为_________.
【答案】,.
【分析】先将原方程化为,即可类比题目中解方程的方法求解即可.
【详解】解:,
,
合并同类项,得,
移项,得,
解得,.
故答案为:,.
【点睛】本题考查了利用平方根解方程及整式的乘法运算,掌握平方根的定义是解答此题的关键.
15.(2022·福建·厦门外国语学校七年级期末)如图,边长为(m+3)的正方形纸片剪出一个边长为m的正方形之后,剩余部分又剪拼成一个长方形(不重叠无缝隙),则拼成的长方形的周长是_________.
【答案】4m+12##12+4m
【分析】根据面积的和差,可得长方形的面积,根据长方形的面积公式,可得长方形的长,根据长方形的周长公式,可得答案.
【详解】解:由面积的和差,得
长方形的面积为(m+3)2-m2=(m+3+m)(m+3-m)=3(2m+3).
由长方形的宽为3,可得长方形的长是(2m+3),
长方形的周长是2[(2m+3)+3]=4m+12.
故答案为:4m+12.
【点睛】本题考查了平方差公式的几何背景,整式的加减,利用了面积的和差.熟练掌握运算法则是解本题的关键.
16.(2021·山东莱西·七年级期中)已知ab=2,=,则多项式a3b+2a2b2+ab3的值为______.
【答案】18
【分析】已知第二个等式左边通分并利用同分母分式的加法法则计算,把ab=2代入求出a+b的值,原式提取公因式,再利用完全平方公式分解后代入计算即可求出值.
【详解】解:∵ab=2,,
∴,即a+b=3,
则原式=ab(a2+2ab+b2)
=ab(a+b)2
=2×32
=2×9
=18.
故答案为:18.
【点睛】本题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.
17.(2021·江苏·无锡市天一实验学校七年级期中)熔喷布,俗称口罩的“心脏”,是口罩中间的过滤层,能过滤细菌,阻止病菌传播.经测量,医用外科口罩的熔喷布厚度约为0.000156米,将0.000156用科学记数法表示应为__________.
【答案】
【分析】科学计数法指的是将一个数表示成a与10的n次幂相乘的形式(,a不为分数形式,n为整数),即可求出答案.
【详解】解:题中,其中a=1.56,n=-4,满足科学计数法要求,
故答案为:.
【点睛】本题主要考察了科学计数法的表示方法,要清楚地知道科学计数法是将一个数表示成a与10的n次幂相乘的形式(,a不为分数形式,n为整数),其中a、n必须要满足上述条件.
18.(2021·北京·七年级期末)某中学要举行校庆活动,现计划在教学楼之间的广场上搭建舞台.已知广场中心有一座边长为的正方形的花坛.学生会提出两个方案:方案一:如图1,围绕花坛搭建外围为正方形的“回”字形舞台(阴影部分),舞台的面积记为;方案二:如图2,在花坛的三面搭建“凹”字形舞台(阴影部分),舞台的面积记为;具体数据如图所示,则______.(填“”,“”或“”)
【答案】
【分析】由题意直接根据正方形和长方形的面积公式即可得到结论.
【详解】解:方案一:如图1,,
方案二:如图2,,
,
.
故答案为:.
【点睛】本题考查了图形的面积,正确识别图形是解题的关键.
三、解答题:本题共7个小题,19-23每题7分,24小题9分,25每题12分,共56分。
19.(2021·江苏海门·七年级期中)计算:
(1)(﹣2x2y)3(3xy2)2﹣12x3y3(﹣5x5y4)
(2)(﹣15x4y2+12x3y3﹣6x2y3)÷(﹣3x2y)
(3)4(a﹣b)2﹣(2a+b)(﹣b+2a)
【答案】(1);(2);(3)
【分析】
(1)先算乘方,再算乘法,最后合并同类项即可.
(2)根据多项式除以单项式法则求出即可.
(3)先算乘方和乘法,再合并同类项即可.
【详解】(1)解:
(2)
解:
(3)
解:
【点睛】本题考查了整式的混合运算,能灵活运用整式的运算法则进行化简是解此题的关键.
20.(2021·全国·七年级单元测试)因式分解
(1)
(2)
(3)
(4)
【答案】(1);(2);(3);(4)
【分析】
(1)利用完全平方公式进行分解因式.
(2)含有公因式2,因此先提取公因式,再利用平方差公式分解因式.
(3)含有公因式2xy,因此先提取公因式,再利用完全平方公式进行分解因式.
(4)含有公因式(a-b),因此先提取公因式,再利用平方差公式分解因式.
【详解】解:(1)
(2).
(3)原式
(4)原式=
【点睛】本题主要考查提公因式法与公式法因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.
21.(2022·吉林市第五中学七年级期末)如图1,有甲、乙、丙三种纸片,其中甲是边长为a的正方形,乙是长为a,宽为b的长方形,丙是边长为b的正方形(a>b).
(1)如图2,用甲、丙纸片各1张,乙纸片2张,可以紧密拼接成一个大正方形,请根据图形的面积写出一个乘法公式 ;
(2)若要用这三种纸片紧密拼接成一个边长为(2a+b)大正方形,则需要取甲、乙、丙纸片各多少张.
【答案】(1)(a+b)2=a2+2ab+b2
(2)需要取甲种纸片4张、乙种纸片4张、丙种纸片1张.
【分析】
(1)根据两种计算图2面积的方法可得公式(a+b)2=a2+2ab+b2;
(2)由计算(2a+b)2的结果可得此题结果.
【详解】(1)解:∵图2中正方形的面积可表示为:(a+b)2和a2+2ab+b2,
∴可得公式(a+b)2=a2+2ab+b2,
故答案为:(a+b)2=a2+2ab+b2;
(2)
解:由计算(2a+b)2=4a2+4ab+b2可得,
需要取甲种纸片4张、乙种纸片4张、丙种纸片1张.
【点睛】本题考查了完全平方公式几何背景的应用能力,关键是能准确地根据图形列出算式,和根据算式得到相应的图形.
22.(2021·全国·七年级单元测试)阅读下列材料:
①关于x的方程方程两边同时乘以得:,即,故,所以.
②;.
根据以上材料,解答下列问题:
(1),则______ ;______ ;______ ;
(2),求的值.
【答案】(1)4, 14,194;(2)
【分析】
(1)根据例题方程两边同时除以x,即可求得的值,然后平方即可求得的值,然后再平方求得的值;
(2)首先方程两边除以2x即可求得的值,然后平方即可求得的值,,然后利用题目提供的立方差公式求解.
【详解】解:(1)∵,
∴,
,
;
故答案为:4;14;194;
(2)∵,
∴,
,
.
【点睛】本题考查了完全平方公式、平方差公式以及立方差公式,正确理解完全平方公式的变形是关键.
23.(2022·福建·泉州五中七年级期末)对于一个图形,通过不同的方法计算图形的面积,就可以得到一个数学等式.
(1)模拟练习:如图,写出一个我们熟悉的数学公式: ;
(2)解决问题:如果,求的值;
(3)类比探究:如果一个长方形的长和宽分别为和,且,求这个长方形的面积.
【答案】(1)(a+b)2=a2+2ab+b2;(2)39;(3)8
【分析】
(1)根据图形的面积的两种不同计算方法得到完全平方公式;
(2)根据完全平方公式变形即可求解;
(3)根据长方形的周长和面积公式以及完全平方公式即可得到结论.
【详解】(1)解:如图,写出一个我们熟悉的数学公式:(a+b)2=a2+2ab+b2.
故答案为:(a+b)2=a2+2ab+b2;
(2)
∵a+b=,ab=12,
∴a2+b2=(a+b)2-2ab=63-24=39;
(3)
设8-x=a,x-2=b,
∵长方形的两邻边分别是8-x,x-2,
∴a+b=8-x+x-2=6,
∵(8-x)2+(x-2)2=a2+b2=(a+b)2-2ab=62-2ab=20,
∴ab=8,
∴这个长方形的面积=(8-x)(x-2)=ab=8.
【点睛】本题考查了因式分解的应用,完全平方公式,熟练掌握完全平方公式是解题的关键.
24.(2021·上海浦东新·七年级期中)数学课上,王老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b,宽为a的长方形.并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积:
方法1: ;
方法2: ;
(2)观察图2,请你写出代数式:(a+b)2,a2+b2,ab之间的等量关系 ;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,(a﹣b)2=13,求ab的值;
②已知(2021﹣a)2+(a﹣2022)2=5,求(2021﹣a)(a﹣2022)的值.
【答案】(1);;(2)(3)①;②-2
【分析】
(1)方法1,由大正方形的边长为(a+b),直接求面积;方法2,大正方形是由2个长方形,2个小正方形拼成,分别求出各个小长方形、正方形的面积再求和即可;
(2)由(1)直接可得关系式;
(3)①由(a-b)2=a2+b2-2ab=13,(a+b)2=a2+b2+2ab=25,两式子直接作差即可求解;②设2021-a=x,a-2022=y,可得x+y=1,再由已知可得x2+y2=5,先求出xy=-2,再求(2021-a)(a-2022)=-2即可.
【详解】解:(1)方法一:∵大正方形的边长为(a+b),
∴S=(a+b)2;
方法二:大正方形是由2个长方形,2个小正方形拼成,
∴S=b2+ab+ab+a2=a2+b2+2ab;
故答案为:(a+b)2,a2+b2+2ab;
(2)
由(1)可得(a+b)2=a2+b2+2ab;
故答案为:(a+b)2=a2+b2+2ab;
(3)
①∵(a-b)2=a2+b2-2ab=13①,
(a+b)2=a2+b2+2ab=25②,
由①-②得,-4ab=-12,
解得:ab=3;
②设2021-a=x,a-2022=y,
∴x+y=1,
∵(2021-a)2+(a-2022)2=5,
∴x2+y2=5,
∵(x+y)2=x2+2xy+y2=1,
∴2xy=1-(x2+y2)=1-5=-4,
解得:xy=-2,
∴(2021-a)(a-2022)=-2.
【点睛】本题考查完全平方公式的几何背景,熟练掌握正方形、长方形面积的求法,灵活应用完全平方公式的变形是解题的关键.
25.(2022·广东乐昌·七年级期末)教科书中这样写道:“我们把多项式及叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.能解决一些与非负数有关的问题或求代数式最大值,最小值等.
例如:分解因式.
原式
例如.求代数式的最小值.
原式
.
可知当时,有最小值,最小值是-3.
(1)分解因式:__________.
(2)试说明:、取任何实数时,多项式的值总为正数.
(3)当,为何值时,多项式有最小值,并求出这个最小值.
【答案】(1)(a-3)(a+1);(2)见解析;(3)m=6,n=4,最小值为5.
【分析】
(1)把a -2a-3化为a -2a+1-4的形式,先用完全平方公式,再用平方差公式因式分解;
(2)首先把x +y -4x+2y+6配方写成(x-2)2+(y+1)2+1,根据平方的非负性即可求解;
(3)用拆项的方法首先把多项式化为m2-2m(n+2)+(n+2)2+n2-8n+16+5的形式,进一步分解因式,再根据平方的非负性求出多项式最小值.
【详解】(1)解:a -2a-3
=a -2a+1-4
=(a-1)2-4
=(a-1-2)(a-1+2)
=(a-3)(a+1);
(2)
解:多项式x +y -4x+2y+6的值总为正数,理由:
x +y -4x+2y+6
=x -4x+4+y +2y+1+1
=(x-2)2+(y+1)2+1,
∵(x-2)2≥0,(y+1)2≥0,
∴(x-2)2+(y+1)2+1≥1,
∴多项式x +y -4x+2y+6的值总为正数;
(3)
解:m -2mn+2n -4m-4n+25
=m2-2m(n+2)+(n+2)2+n2-8n+16+5
=(m-n-2)2+(n-4)2+5,
当m-n-2=0,n-4=0时代数式有最小值,
解得m=6,n=4,最小值为5.
【点睛】本题主要考查了因式分解的应用、非负数的性质:偶次方、完全平方式,熟练掌握这三个知识点的综合应用,用拆项法把多项式化为完全平方的形式是解题关键
一、单选题:本题共10个小题,每小题2分,共20分。在每小题给出的四个选项中只有一项是符合题目要求的。
1.(2022·全国·七年级期末)如果xm=2,xn=,那么xm+n的值为( )
A.2 B.8 C. D.2
(2021·广东番禺·七年级期末)下列运算中正确的是( ).
A. B. C. D.
3.(2022·上海金山·七年级期中)下列计算正确的是( )
A. B.
C. D.
4.(2022·湖北潜江·七年级期末)如果,那么代数式的值为( )
A. B. C.6 D.8
5.(2022·湖南·七年级单元测试)已知x+y=4 ,xy=3 ,则x2+ y2的值为( )
A.22 B.16 C.10 D.4
6.(2021·北京·七年级期中)如图,由4个全等的小长方形与1个小正方形密铺成正方形图案,该图案的面积为49,小正方形的面积为4,若分别用,表示小长方形的长和宽,则下列关系式中不正确的是( )
A. B. C. D.
7.(2022·广东中山·七年级期末)如图,两个正方形的边长分别为a、b,若,,则阴影部分的面积是( )
A.40 B. C.20 D.23
(2022·全国·七年级单元测试)下列各式从左到右的变形中,是因式分解的为( ).
A. B.
C. D.
9.(2022·山西·七年级期末)英国曼彻斯特大学的两位科学家因为成功地从石墨中分离出石墨烯,荣获了诺贝尔物理学奖.石墨烯是目前世上最薄却也是最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.00000034毫米,将数0.00000034用科学记数法表示为( )
A. B. C. D.
10.(2021·全国·七年级单元测试)如图,在边长为的正方形中挖掉一个边长为的小正方形,把余下的部分剪成一个矩形,通过计算两个图形(阴影部分)的面积,验证了一个等式是( )
A. B.
C. D.
二、填空题:本题共8个小题,每题3分,共24分。
11.(2021·北京·七年级期中)若,,则的值为 __.
12.(2021·广东茂南·七年级期末)若单项式与b的和仍是单项式,则的值是________.
13.(2021·全国·七年级单元测试)若长方形的面积是6a3+5ab+3a,长为3a,则它的宽为____.
14.(2021·全国·七年级单元测试)旧知回顾:在七年级学方根”时,我们会直接开方解形如的方程(解为).解题运用:方程解为_________.
15.(2022·福建·厦门外国语学校七年级期末)如图,边长为(m+3)的正方形纸片剪出一个边长为m的正方形之后,剩余部分又剪拼成一个长方形(不重叠无缝隙),则拼成的长方形的周长是_________.
16.(2021·山东莱西·七年级期中)已知ab=2,=,则多项式a3b+2a2b2+ab3的值为______.
17.(2021·江苏·无锡市天一实验学校七年级期中)熔喷布,俗称口罩的“心脏”,是口罩中间的过滤层,能过滤细菌,阻止病菌传播.经测量,医用外科口罩的熔喷布厚度约为0.000156米,将0.000156用科学记数法表示应为__________.
18.(2021·北京·七年级期末)某中学要举行校庆活动,现计划在教学楼之间的广场上搭建舞台.已知广场中心有一座边长为的正方形的花坛.学生会提出两个方案:方案一:如图1,围绕花坛搭建外围为正方形的“回”字形舞台(阴影部分),舞台的面积记为;方案二:如图2,在花坛的三面搭建“凹”字形舞台(阴影部分),舞台的面积记为;具体数据如图所示,则______.(填“”,“”或“”)
三、解答题:本题共7个小题,19-23每题7分,24小题9分,25每题12分,共56分。
19.(2021·江苏海门·七年级期中)计算:
(1)(﹣2x2y)3(3xy2)2﹣12x3y3(﹣5x5y4)
(2)(﹣15x4y2+12x3y3﹣6x2y3)÷(﹣3x2y)
(3)4(a﹣b)2﹣(2a+b)(﹣b+2a)
20.(2021·全国·七年级单元测试)因式分解
(1)
(2)
(3)
(4)
21.(2022·吉林市第五中学七年级期末)如图1,有甲、乙、丙三种纸片,其中甲是边长为a的正方形,乙是长为a,宽为b的长方形,丙是边长为b的正方形(a>b).
(1)如图2,用甲、丙纸片各1张,乙纸片2张,可以紧密拼接成一个大正方形,请根据图形的面积写出一个乘法公式 ;
(2)若要用这三种纸片紧密拼接成一个边长为(2a+b)大正方形,则需要取甲、乙、丙纸片各多少张.
22.(2021·全国·七年级单元测试)阅读下列材料:
①关于x的方程方程两边同时乘以得:,即,故,所以.
②;.
根据以上材料,解答下列问题:
(1),则______ ;______ ;______ ;
(2),求的值.
23.(2022·福建·泉州五中七年级期末)对于一个图形,通过不同的方法计算图形的面积,就可以得到一个数学等式.
(1)模拟练习:如图,写出一个我们熟悉的数学公式: ;
(2)解决问题:如果,求的值;
(3)类比探究:如果一个长方形的长和宽分别为和,且,求这个长方形的面积.
24.(2021·上海浦东新·七年级期中)数学课上,王老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b,宽为a的长方形.并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积:
方法1: ;
方法2: ;
(2)观察图2,请你写出代数式:(a+b)2,a2+b2,ab之间的等量关系 ;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,(a﹣b)2=13,求ab的值;
②已知(2021﹣a)2+(a﹣2022)2=5,求(2021﹣a)(a﹣2022)的值.
25.(2022·广东乐昌·七年级期末)教科书中这样写道:“我们把多项式及叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.能解决一些与非负数有关的问题或求代数式最大值,最小值等.
例如:分解因式.
原式
例如.求代数式的最小值.
原式
.
可知当时,有最小值,最小值是-3.
(1)分解因式:__________.
(2)试说明:、取任何实数时,多项式的值总为正数.
(3)当,为何值时,多项式有最小值,并求出这个最小值.
第8章 整式乘法和因式分解 单元测试
单选题:本题共10个小题,每小题2分,共20分。在每小题给出的四个选项中只有一项是符合题目要求的。
1.(2022·全国·七年级期末)如果xm=2,xn=,那么xm+n的值为( )
A.2 B.8 C. D.2
【答案】C
【分析】根据同底数幂的乘法进行运算即可.
【详解】解:如果xm=2,xn=,
那么xm+n=xm×xn=2×=.
故选:C.
【点睛】本题考查了同底数幂的乘法,解题的关键是熟练掌握同底数幂的乘法公式.
(2021·广东番禺·七年级期末)下列运算中正确的是( ).
A. B. C. D.
【答案】D
【分析】根据同底数相乘,幂的乘方,积的乘方,同底数相除法则,逐项判断即可求解.
【详解】解:A、,故本选项错误,不符合题意;B、,故本选项错误,不符合题意;
C、,故本选项错误,不符合题意;D、,故本选项正确,符合题意;
故选:D
【点睛】本题主要考查了同底数相乘,幂的乘方,积的乘方,同底数相除法则,熟练掌握同底数相乘,幂的乘方,积的乘方,同底数相除法则是解题的关键.
3.(2022·上海金山·七年级期中)下列计算正确的是( )
A. B.
C. D.
【答案】B
【分析】利用合并同类项的法则,单项式乘单项式的法则,多项式乘多项式的法则对各项进行运算即可.
【详解】解:A、2x+3x=5x,故A不符合题意;B、2a2 3a=6a3,故B符合题意;C、(x-2)(x+3)=x2+x-6,故C不符合题意;D、2x3 3x2=6x5,故D不符合题意;
故选:B.
【点睛】本题主要考查合并同类项,单项式乘单项式,多项式乘多项式,解答的关键是对相应的运算法则的掌握.
4.(2022·湖北潜江·七年级期末)如果,那么代数式的值为( )
A. B. C.6 D.8
【答案】D
【分析】先将原式根据单项式乘以多项式法则及完全平方公式法则去括号,合并同类项,再将式子的值代入计算求出答案.
【详解】解:∵
=
=
=
∵,
∴原式==8,
故选:D.
【点睛】此题考查了已知式子的值求代数式的值,正确掌握整式的混合运算法则是解题的关键.
5.(2022·湖南·七年级单元测试)已知x+y=4 ,xy=3 ,则x2+ y2的值为( )
A.22 B.16 C.10 D.4
【答案】C
【分析】根据完全平方公式变形,整体代入求值即可.
【详解】解:.
故选择C.
【点睛】本题考查式子的值,求代数式的值,掌握完全平方公式变形的方法是解题关键.
6.(2021·北京·七年级期中)如图,由4个全等的小长方形与1个小正方形密铺成正方形图案,该图案的面积为49,小正方形的面积为4,若分别用,表示小长方形的长和宽,则下列关系式中不正确的是( )
A. B. C. D.
【答案】C
【分析】根据完全平方公式及图形的特点找到长度关系即可依次判断.
【详解】解:、因为正方形图案的边长7,同时还可用来表示,故,正确;、由图象可知,即,正确;、由和,可得,,错误;、由,,可得,,所以,正确.
故选:.
【点睛】本题主要考查了完全平方公式的几何背景,解答本题需结合图形,利用等式的变形来解决问题.
7.(2022·广东中山·七年级期末)如图,两个正方形的边长分别为a、b,若,,则阴影部分的面积是( )
A.40 B. C.20 D.23
【答案】C
【分析】根据阴影部分面积等于2个正方形面积减去2个空白部分的三角形面积,进而根据完全平方公式的变形求解即可
【详解】解:阴影部分面积等于
∵,,
∴阴影部分面积等于
故答案为:C
【点睛】本题考查了完全平方公式变形求图形面积,掌握完全平方公式是解题的关键.
(2022·全国·七年级单元测试)下列各式从左到右的变形中,是因式分解的为( ).
A. B.
C. D.
【答案】B
【分析】根据因式分解的定义把一个多项式化成几个整式的积的形式,叫因式分解.然后对各选项逐个判断即可.
【详解】解:A、两因式之间用加号连结,是和的形式不是因式分解,故本选项不符合题意;B、是因式分解,故本选项符合题意;C、将积化为和差形式,是多项式乘法运算,不是因式分解,故本选项不符合题意;D、两因式之间用加号连结,是和的形式,不是因式分解,故本选项不符合题意;
故选:B.
【点睛】本题考查了因式分解的定义,能熟记因式分解的定义的内容是解此题的关键 .
9.(2022·山西·七年级期末)英国曼彻斯特大学的两位科学家因为成功地从石墨中分离出石墨烯,荣获了诺贝尔物理学奖.石墨烯是目前世上最薄却也是最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.00000034毫米,将数0.00000034用科学记数法表示为( )
A. B. C. D.
【答案】D
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10 n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【详解】解:0.00000034=,
故选:D.
【点睛】本题考查用科学记数法表示较小的数,一般形式为a×10 n,其中1≤a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
10.(2021·全国·七年级单元测试)如图,在边长为的正方形中挖掉一个边长为的小正方形,把余下的部分剪成一个矩形,通过计算两个图形(阴影部分)的面积,验证了一个等式是( )
A. B.
C. D.
【答案】A
【分析】左图中阴影部分的面积=a2 b2,右图中矩形面积=(a+b)(a b),根据二者面积相等,即可解答.
【详解】解:由题意可得:a2 b2=(a b)(a+b).
故选:A.
【点睛】此题主要考查了乘法的平方差公式,属于基础题型.
二、填空题:本题共8个小题,每题3分,共24分。
11.(2021·北京·七年级期中)若,,则的值为 __.
【答案】
【分析】逆向运用同底数幂的除法法则以及利用幂的乘方运算法则解答即可,同底数幂的除法法则:底数不变,指数相减;幂的乘方法则:底数不变,指数相乘.
【详解】解:,
,
解得,
,
.
故答案为:2.
【点睛】本题考查了同底数幂的除法以及幂的乘方,掌握幂的运算法则是解答本题的关键.
12.(2021·广东茂南·七年级期末)若单项式与b的和仍是单项式,则的值是________.
【答案】1
【分析】由题意知与是同类项,有,求出的值,然后代入求解即可.
【详解】解:由题意知与是同类项
∴
解得
∴
故答案为:1.
【点睛】本题考查了同类项,0指数幂.解题的关键在于正确的计算.
13.(2021·全国·七年级单元测试)若长方形的面积是6a3+5ab+3a,长为3a,则它的宽为____.
【答案】2a2+b+1
【分析】根据整式的除法即可求出答案.
【详解】解:(6a3+5ab+3a)÷3a
=2a2+b+1,
故答案为:2a2+b+1.
【点睛】本题考查整式的运算,解题的关键是熟练运用整式的除法法则,本题属于基础题型.
14.(2021·全国·七年级单元测试)旧知回顾:在七年级学方根”时,我们会直接开方解形如的方程(解为).解题运用:方程解为_________.
【答案】,.
【分析】先将原方程化为,即可类比题目中解方程的方法求解即可.
【详解】解:,
,
合并同类项,得,
移项,得,
解得,.
故答案为:,.
【点睛】本题考查了利用平方根解方程及整式的乘法运算,掌握平方根的定义是解答此题的关键.
15.(2022·福建·厦门外国语学校七年级期末)如图,边长为(m+3)的正方形纸片剪出一个边长为m的正方形之后,剩余部分又剪拼成一个长方形(不重叠无缝隙),则拼成的长方形的周长是_________.
【答案】4m+12##12+4m
【分析】根据面积的和差,可得长方形的面积,根据长方形的面积公式,可得长方形的长,根据长方形的周长公式,可得答案.
【详解】解:由面积的和差,得
长方形的面积为(m+3)2-m2=(m+3+m)(m+3-m)=3(2m+3).
由长方形的宽为3,可得长方形的长是(2m+3),
长方形的周长是2[(2m+3)+3]=4m+12.
故答案为:4m+12.
【点睛】本题考查了平方差公式的几何背景,整式的加减,利用了面积的和差.熟练掌握运算法则是解本题的关键.
16.(2021·山东莱西·七年级期中)已知ab=2,=,则多项式a3b+2a2b2+ab3的值为______.
【答案】18
【分析】已知第二个等式左边通分并利用同分母分式的加法法则计算,把ab=2代入求出a+b的值,原式提取公因式,再利用完全平方公式分解后代入计算即可求出值.
【详解】解:∵ab=2,,
∴,即a+b=3,
则原式=ab(a2+2ab+b2)
=ab(a+b)2
=2×32
=2×9
=18.
故答案为:18.
【点睛】本题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.
17.(2021·江苏·无锡市天一实验学校七年级期中)熔喷布,俗称口罩的“心脏”,是口罩中间的过滤层,能过滤细菌,阻止病菌传播.经测量,医用外科口罩的熔喷布厚度约为0.000156米,将0.000156用科学记数法表示应为__________.
【答案】
【分析】科学计数法指的是将一个数表示成a与10的n次幂相乘的形式(,a不为分数形式,n为整数),即可求出答案.
【详解】解:题中,其中a=1.56,n=-4,满足科学计数法要求,
故答案为:.
【点睛】本题主要考察了科学计数法的表示方法,要清楚地知道科学计数法是将一个数表示成a与10的n次幂相乘的形式(,a不为分数形式,n为整数),其中a、n必须要满足上述条件.
18.(2021·北京·七年级期末)某中学要举行校庆活动,现计划在教学楼之间的广场上搭建舞台.已知广场中心有一座边长为的正方形的花坛.学生会提出两个方案:方案一:如图1,围绕花坛搭建外围为正方形的“回”字形舞台(阴影部分),舞台的面积记为;方案二:如图2,在花坛的三面搭建“凹”字形舞台(阴影部分),舞台的面积记为;具体数据如图所示,则______.(填“”,“”或“”)
【答案】
【分析】由题意直接根据正方形和长方形的面积公式即可得到结论.
【详解】解:方案一:如图1,,
方案二:如图2,,
,
.
故答案为:.
【点睛】本题考查了图形的面积,正确识别图形是解题的关键.
三、解答题:本题共7个小题,19-23每题7分,24小题9分,25每题12分,共56分。
19.(2021·江苏海门·七年级期中)计算:
(1)(﹣2x2y)3(3xy2)2﹣12x3y3(﹣5x5y4)
(2)(﹣15x4y2+12x3y3﹣6x2y3)÷(﹣3x2y)
(3)4(a﹣b)2﹣(2a+b)(﹣b+2a)
【答案】(1);(2);(3)
【分析】
(1)先算乘方,再算乘法,最后合并同类项即可.
(2)根据多项式除以单项式法则求出即可.
(3)先算乘方和乘法,再合并同类项即可.
【详解】(1)解:
(2)
解:
(3)
解:
【点睛】本题考查了整式的混合运算,能灵活运用整式的运算法则进行化简是解此题的关键.
20.(2021·全国·七年级单元测试)因式分解
(1)
(2)
(3)
(4)
【答案】(1);(2);(3);(4)
【分析】
(1)利用完全平方公式进行分解因式.
(2)含有公因式2,因此先提取公因式,再利用平方差公式分解因式.
(3)含有公因式2xy,因此先提取公因式,再利用完全平方公式进行分解因式.
(4)含有公因式(a-b),因此先提取公因式,再利用平方差公式分解因式.
【详解】解:(1)
(2).
(3)原式
(4)原式=
【点睛】本题主要考查提公因式法与公式法因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.
21.(2022·吉林市第五中学七年级期末)如图1,有甲、乙、丙三种纸片,其中甲是边长为a的正方形,乙是长为a,宽为b的长方形,丙是边长为b的正方形(a>b).
(1)如图2,用甲、丙纸片各1张,乙纸片2张,可以紧密拼接成一个大正方形,请根据图形的面积写出一个乘法公式 ;
(2)若要用这三种纸片紧密拼接成一个边长为(2a+b)大正方形,则需要取甲、乙、丙纸片各多少张.
【答案】(1)(a+b)2=a2+2ab+b2
(2)需要取甲种纸片4张、乙种纸片4张、丙种纸片1张.
【分析】
(1)根据两种计算图2面积的方法可得公式(a+b)2=a2+2ab+b2;
(2)由计算(2a+b)2的结果可得此题结果.
【详解】(1)解:∵图2中正方形的面积可表示为:(a+b)2和a2+2ab+b2,
∴可得公式(a+b)2=a2+2ab+b2,
故答案为:(a+b)2=a2+2ab+b2;
(2)
解:由计算(2a+b)2=4a2+4ab+b2可得,
需要取甲种纸片4张、乙种纸片4张、丙种纸片1张.
【点睛】本题考查了完全平方公式几何背景的应用能力,关键是能准确地根据图形列出算式,和根据算式得到相应的图形.
22.(2021·全国·七年级单元测试)阅读下列材料:
①关于x的方程方程两边同时乘以得:,即,故,所以.
②;.
根据以上材料,解答下列问题:
(1),则______ ;______ ;______ ;
(2),求的值.
【答案】(1)4, 14,194;(2)
【分析】
(1)根据例题方程两边同时除以x,即可求得的值,然后平方即可求得的值,然后再平方求得的值;
(2)首先方程两边除以2x即可求得的值,然后平方即可求得的值,,然后利用题目提供的立方差公式求解.
【详解】解:(1)∵,
∴,
,
;
故答案为:4;14;194;
(2)∵,
∴,
,
.
【点睛】本题考查了完全平方公式、平方差公式以及立方差公式,正确理解完全平方公式的变形是关键.
23.(2022·福建·泉州五中七年级期末)对于一个图形,通过不同的方法计算图形的面积,就可以得到一个数学等式.
(1)模拟练习:如图,写出一个我们熟悉的数学公式: ;
(2)解决问题:如果,求的值;
(3)类比探究:如果一个长方形的长和宽分别为和,且,求这个长方形的面积.
【答案】(1)(a+b)2=a2+2ab+b2;(2)39;(3)8
【分析】
(1)根据图形的面积的两种不同计算方法得到完全平方公式;
(2)根据完全平方公式变形即可求解;
(3)根据长方形的周长和面积公式以及完全平方公式即可得到结论.
【详解】(1)解:如图,写出一个我们熟悉的数学公式:(a+b)2=a2+2ab+b2.
故答案为:(a+b)2=a2+2ab+b2;
(2)
∵a+b=,ab=12,
∴a2+b2=(a+b)2-2ab=63-24=39;
(3)
设8-x=a,x-2=b,
∵长方形的两邻边分别是8-x,x-2,
∴a+b=8-x+x-2=6,
∵(8-x)2+(x-2)2=a2+b2=(a+b)2-2ab=62-2ab=20,
∴ab=8,
∴这个长方形的面积=(8-x)(x-2)=ab=8.
【点睛】本题考查了因式分解的应用,完全平方公式,熟练掌握完全平方公式是解题的关键.
24.(2021·上海浦东新·七年级期中)数学课上,王老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b,宽为a的长方形.并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积:
方法1: ;
方法2: ;
(2)观察图2,请你写出代数式:(a+b)2,a2+b2,ab之间的等量关系 ;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,(a﹣b)2=13,求ab的值;
②已知(2021﹣a)2+(a﹣2022)2=5,求(2021﹣a)(a﹣2022)的值.
【答案】(1);;(2)(3)①;②-2
【分析】
(1)方法1,由大正方形的边长为(a+b),直接求面积;方法2,大正方形是由2个长方形,2个小正方形拼成,分别求出各个小长方形、正方形的面积再求和即可;
(2)由(1)直接可得关系式;
(3)①由(a-b)2=a2+b2-2ab=13,(a+b)2=a2+b2+2ab=25,两式子直接作差即可求解;②设2021-a=x,a-2022=y,可得x+y=1,再由已知可得x2+y2=5,先求出xy=-2,再求(2021-a)(a-2022)=-2即可.
【详解】解:(1)方法一:∵大正方形的边长为(a+b),
∴S=(a+b)2;
方法二:大正方形是由2个长方形,2个小正方形拼成,
∴S=b2+ab+ab+a2=a2+b2+2ab;
故答案为:(a+b)2,a2+b2+2ab;
(2)
由(1)可得(a+b)2=a2+b2+2ab;
故答案为:(a+b)2=a2+b2+2ab;
(3)
①∵(a-b)2=a2+b2-2ab=13①,
(a+b)2=a2+b2+2ab=25②,
由①-②得,-4ab=-12,
解得:ab=3;
②设2021-a=x,a-2022=y,
∴x+y=1,
∵(2021-a)2+(a-2022)2=5,
∴x2+y2=5,
∵(x+y)2=x2+2xy+y2=1,
∴2xy=1-(x2+y2)=1-5=-4,
解得:xy=-2,
∴(2021-a)(a-2022)=-2.
【点睛】本题考查完全平方公式的几何背景,熟练掌握正方形、长方形面积的求法,灵活应用完全平方公式的变形是解题的关键.
25.(2022·广东乐昌·七年级期末)教科书中这样写道:“我们把多项式及叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.能解决一些与非负数有关的问题或求代数式最大值,最小值等.
例如:分解因式.
原式
例如.求代数式的最小值.
原式
.
可知当时,有最小值,最小值是-3.
(1)分解因式:__________.
(2)试说明:、取任何实数时,多项式的值总为正数.
(3)当,为何值时,多项式有最小值,并求出这个最小值.
【答案】(1)(a-3)(a+1);(2)见解析;(3)m=6,n=4,最小值为5.
【分析】
(1)把a -2a-3化为a -2a+1-4的形式,先用完全平方公式,再用平方差公式因式分解;
(2)首先把x +y -4x+2y+6配方写成(x-2)2+(y+1)2+1,根据平方的非负性即可求解;
(3)用拆项的方法首先把多项式化为m2-2m(n+2)+(n+2)2+n2-8n+16+5的形式,进一步分解因式,再根据平方的非负性求出多项式最小值.
【详解】(1)解:a -2a-3
=a -2a+1-4
=(a-1)2-4
=(a-1-2)(a-1+2)
=(a-3)(a+1);
(2)
解:多项式x +y -4x+2y+6的值总为正数,理由:
x +y -4x+2y+6
=x -4x+4+y +2y+1+1
=(x-2)2+(y+1)2+1,
∵(x-2)2≥0,(y+1)2≥0,
∴(x-2)2+(y+1)2+1≥1,
∴多项式x +y -4x+2y+6的值总为正数;
(3)
解:m -2mn+2n -4m-4n+25
=m2-2m(n+2)+(n+2)2+n2-8n+16+5
=(m-n-2)2+(n-4)2+5,
当m-n-2=0,n-4=0时代数式有最小值,
解得m=6,n=4,最小值为5.
【点睛】本题主要考查了因式分解的应用、非负数的性质:偶次方、完全平方式,熟练掌握这三个知识点的综合应用,用拆项法把多项式化为完全平方的形式是解题关键
