九年级下册数学第三章圆单元测试四(附答案)
文档属性
| 名称 | 九年级下册数学第三章圆单元测试四(附答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 246.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-18 00:00:00 | ||
图片预览


文档简介
九年级数学《圆》单元测试四
学校:___________姓名:___________班级:___________考号:___________
一、选择题
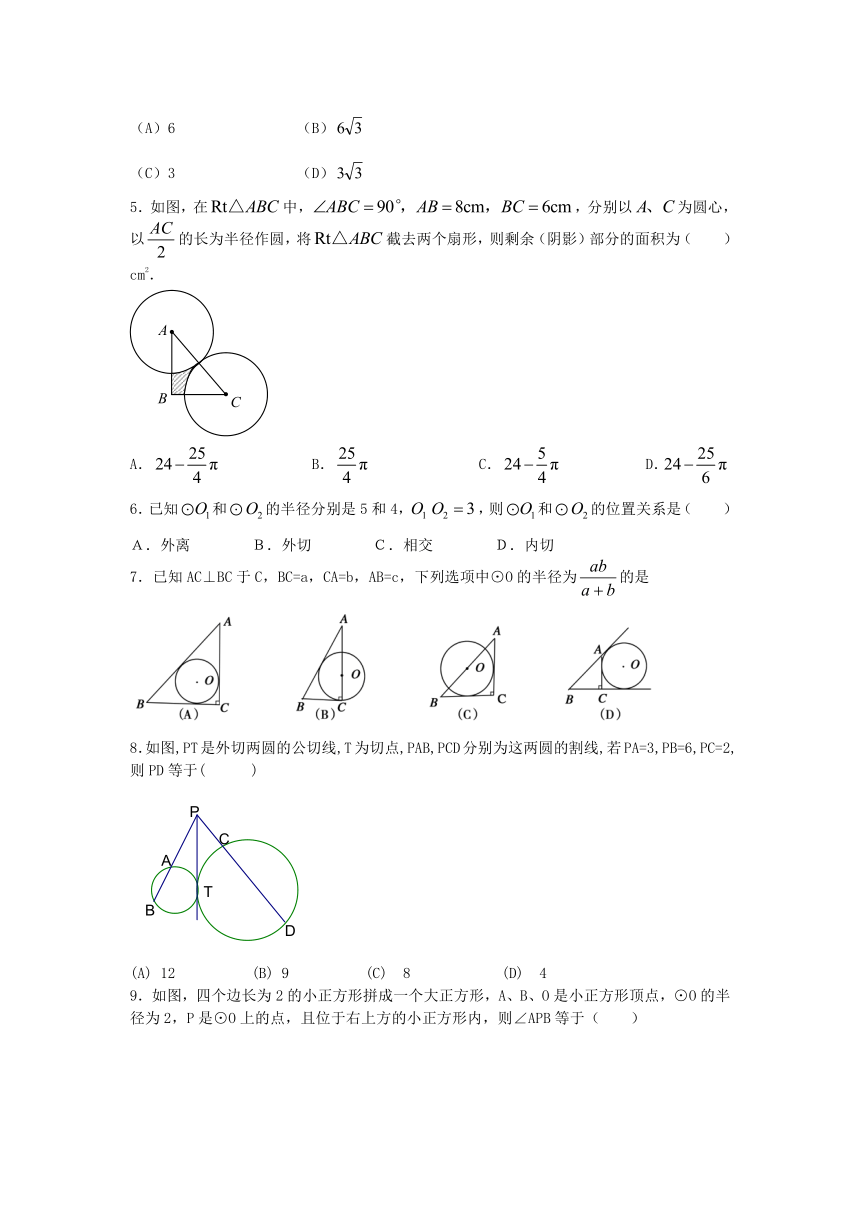
1.如图,在以原点为圆心,2为半径的⊙O上有一点C,∠COA=45°,则C的坐标为( )
A. ( ,) B. (,-) C. (-,) D.(-,-)
2.如图,两个同心圆的半径分别为4cm和5cm,大圆的一条弦AB与小圆相切,则弦AB的长为【 】
A.3cm B.4cm C.6cm D.8cm
3.如图,在△ABC中,∠C =90°,AC>BC,若以AC为底面圆的半径,BC为高的圆锥的侧面积为S1,若以BC为底面圆的半径,AC为高的圆锥的侧面积为S2 ,则( )
A.S1 =S2 B.S1 >S2 C.S1 <S2 D.S1 ,S2的大小大小不能确定
4.如图,⊙的直径与弦的夹角为,切线与的延长线交于点,若⊙的半径为3,则的长为
(A)6 (B)
(C)3 (D)
5.如图,在中,,分别以为圆心,以的长为半径作圆,将截去两个扇形,则剩余(阴影)部分的面积为( )cm2.
A. B. C. D.
6.已知和的半径分别是5和4,,则和的位置关系是( )
A.外离 B.外切 C.相交 D.内切
7.已知AC⊥BC于C,BC=a,CA=b,AB=c,下列选项中⊙O的半径为的是
8.如图,PT是外切两圆的公切线,T为切点,PAB,PCD分别为这两圆的割线,若PA=3,PB=6,PC=2,则PD等于( )
(A) 12 (B) 9 (C) 8 (D) 4
9.如图,四个边长为2的小正方形拼成一个大正方形,A、B、O是小正方形顶点,⊙O的半径为2,P是⊙O上的点,且位于右上方的小正方形内,则∠APB等于( )
A.30° B.45° C.60° D.90°
10.奥运会旗上的五环(如图)间的位置关系有( )
A.相交或相切 B.相交或内含 C.相交或外离 D.相切或外离
二、填空题
11.如图,如果正三角形的外接圆⊙O的半径为2,那么该正三角形的边长是 .
12.如图,将三角板的直角顶点放在⊙O的圆心上,两条直角边分别交⊙O于A、B两点,点P在优弧AB上,且与点A、B不重合,连结PA、PB.则∠APB的大小为 °.
13.圆的半径为13 cm,弦AB∥CD,AB=10 cm,CD=24 cm,则弦AB、CD之间的距离是 cm
14.如图,矩形ABCD的长AB=6cm,宽AD=3cm. O是AB的中点,OP⊥AB,两半圆的直径分别为AO与OB.抛物线经过C、D两点,则图中阴影部分的面积是 cm2.
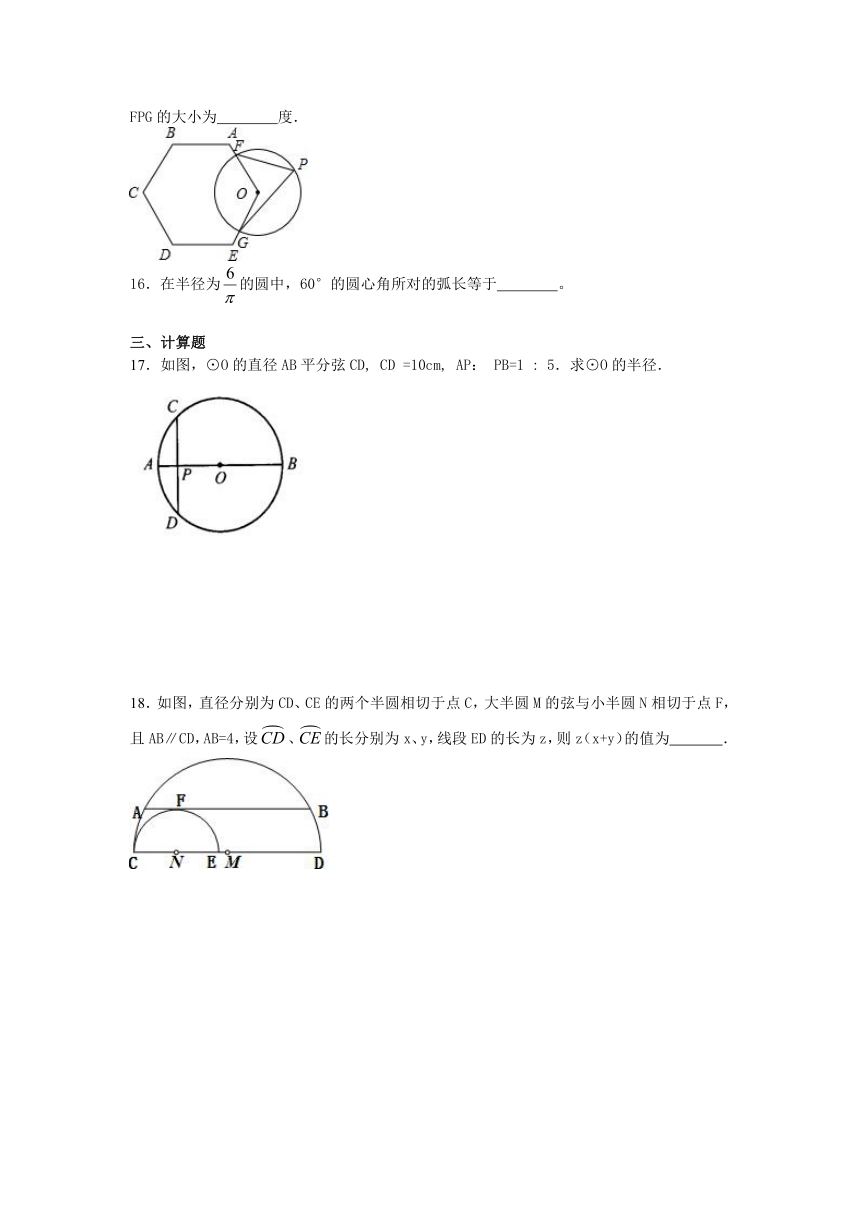
15.如图,⊙O与正六边形OABCDE的边OA、OE分别交于点F、G,则弧所对的圆周角∠FPG的大小为 度.
16.在半径为的圆中,60°的圆心角所对的弧长等于 。
三、计算题
17.如图,⊙O的直径AB平分弦CD, CD =10cm, AP: PB=1 : 5.求⊙O的半径.
18.如图,直径分别为CD、CE的两个半圆相切于点C,大半圆M的弦与小半圆N相切于点F,且AB∥CD,AB=4,设、的长分别为x、y,线段ED的长为z,则z(x+y)的值为 .
四、解答题
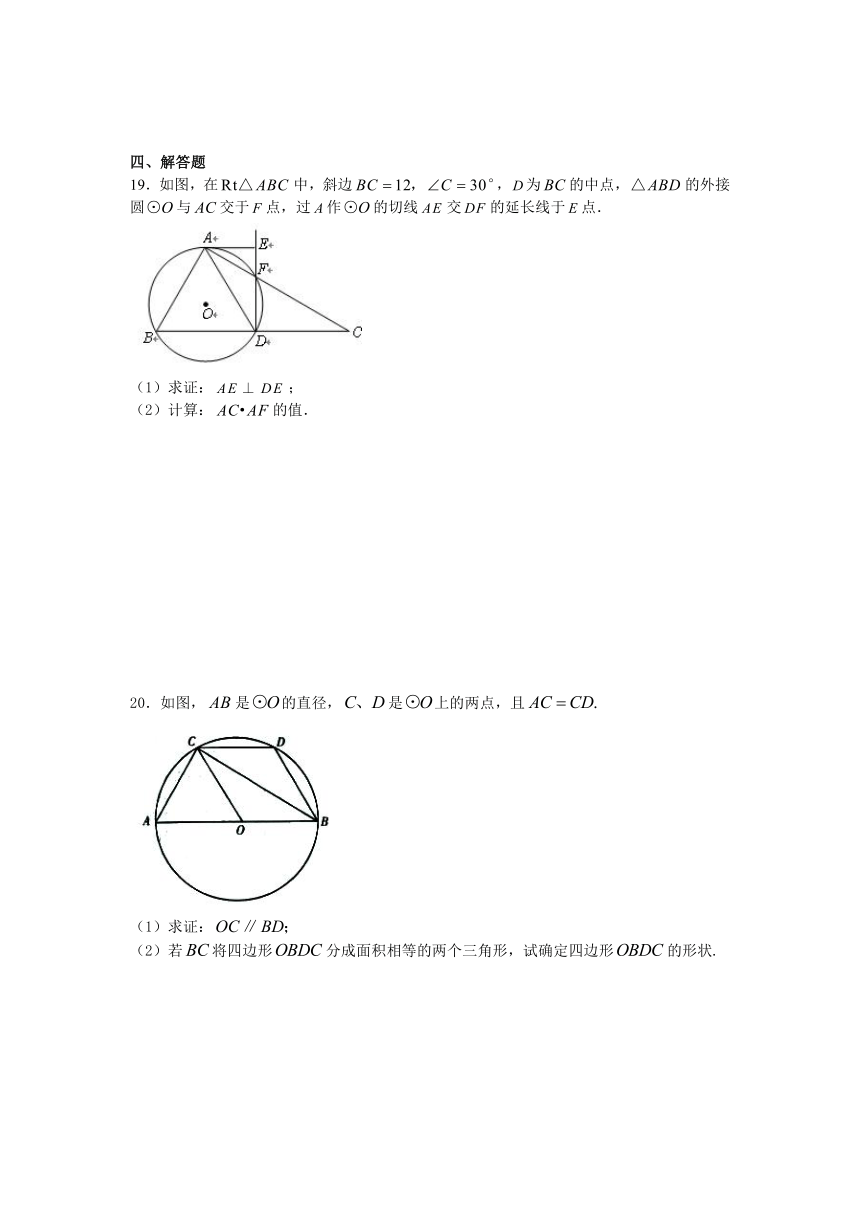
19.如图,在中,斜边,为的中点,的外接圆与交于点,过作的切线交的延长线于点.
(1)求证:;
(2)计算:的值.
20.如图,是的直径,是上的两点,且
(1)求证:
(2)若将四边形分成面积相等的两个三角形,试确定四边形的形状.
21.(1)已知:如图1,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.求证:DE=DF.
(2)如图2,已知△ABC内接于⊙O,AC是⊙O的直径,D是弧AB的中点,过点D作直线BC的垂线,分别交CB,CA的延长线于E,F,求证:EF是⊙O的切线.
22.已知: 如图, AB是⊙O的直径,⊙O过AC的中点D, DE切⊙O于点D, 交BC于点E.
(1)求证: DE⊥BC;
(2)如果CD=4,CE=3,求⊙O的半径.
23.如图,AC是⊙O的直径,弦BD交AC于点E.
(1)求证:△ADE∽△BCE;
(2)若AD2=AC·AE,求证:BC=CD.
24.如图,在同一平面内,有一组平行线l1、l2、l3,相邻两条平行线之间的距离均为4,点O在直线l1上,⊙O与直线l3的交点为A、B,AB=12,求⊙O的半径.
参考答案
1.C
2.C。
3.B
4.D
5.A
6.C
7.C
8.B
9.B
10.C
11.
12.45
13.7或17
14.
15.60。
16.2
17.连接CO,设圆的半径为r,
∵直径AB平分弦CD
∴AB垂直CD
∵AP:PB=1 : 5 ∴PO=r
∴r2=52+(r)2 得r=3
18.解:如图,过M作MG⊥AB于G,连MB,NF,
而AB=4,
∴BG=AG=2,
∴MB2﹣MG2=22=4,
又∵大半圆M的弦与小半圆N相切于点F,
∴NF⊥AB,
∵AB∥CD,
∴MG=NF,
设⊙M,⊙N的半径分别为R,r,
∴z(x+y)=(CD﹣CE)(π?R+π?r),
=(2R﹣2r)(R+r)?π,
=(R2﹣r2)?2π,
=4?2π,
=8π.
19.(1)证明:在中,为的中点,
为等边三角形.
点为的中心(内心,外心,垂心三心合一).
∴连接OA,OB,
又为的切线,
又四边形内接于圆
即
(2)解:由(1)知,为等边三角形.
则
又
20.(1)略(2)菱形
21.略
22.证明:(1)连结OD
∵DE切⊙O于点D
∴DE⊥OD, ∴∠ODE=900 又∵AD=DC, AO=OB
∴OD//BC
∴∠DEC=∠ODE=900, ∴DE⊥BC
(2)连结BD.
∵AB是⊙O的直径, ∴∠ADB=900
∴BD⊥AC, ∴∠BDC=900
又∵DE⊥BC, △RtCDB∽△RtCED
∴, ∴BC=
又∵OD=BC
∴OD=, 即⊙O的半径为
23.略
24.10
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,在以原点为圆心,2为半径的⊙O上有一点C,∠COA=45°,则C的坐标为( )
A. ( ,) B. (,-) C. (-,) D.(-,-)
2.如图,两个同心圆的半径分别为4cm和5cm,大圆的一条弦AB与小圆相切,则弦AB的长为【 】
A.3cm B.4cm C.6cm D.8cm
3.如图,在△ABC中,∠C =90°,AC>BC,若以AC为底面圆的半径,BC为高的圆锥的侧面积为S1,若以BC为底面圆的半径,AC为高的圆锥的侧面积为S2 ,则( )
A.S1 =S2 B.S1 >S2 C.S1 <S2 D.S1 ,S2的大小大小不能确定
4.如图,⊙的直径与弦的夹角为,切线与的延长线交于点,若⊙的半径为3,则的长为
(A)6 (B)
(C)3 (D)
5.如图,在中,,分别以为圆心,以的长为半径作圆,将截去两个扇形,则剩余(阴影)部分的面积为( )cm2.
A. B. C. D.
6.已知和的半径分别是5和4,,则和的位置关系是( )
A.外离 B.外切 C.相交 D.内切
7.已知AC⊥BC于C,BC=a,CA=b,AB=c,下列选项中⊙O的半径为的是
8.如图,PT是外切两圆的公切线,T为切点,PAB,PCD分别为这两圆的割线,若PA=3,PB=6,PC=2,则PD等于( )
(A) 12 (B) 9 (C) 8 (D) 4
9.如图,四个边长为2的小正方形拼成一个大正方形,A、B、O是小正方形顶点,⊙O的半径为2,P是⊙O上的点,且位于右上方的小正方形内,则∠APB等于( )
A.30° B.45° C.60° D.90°
10.奥运会旗上的五环(如图)间的位置关系有( )
A.相交或相切 B.相交或内含 C.相交或外离 D.相切或外离
二、填空题
11.如图,如果正三角形的外接圆⊙O的半径为2,那么该正三角形的边长是 .
12.如图,将三角板的直角顶点放在⊙O的圆心上,两条直角边分别交⊙O于A、B两点,点P在优弧AB上,且与点A、B不重合,连结PA、PB.则∠APB的大小为 °.
13.圆的半径为13 cm,弦AB∥CD,AB=10 cm,CD=24 cm,则弦AB、CD之间的距离是 cm
14.如图,矩形ABCD的长AB=6cm,宽AD=3cm. O是AB的中点,OP⊥AB,两半圆的直径分别为AO与OB.抛物线经过C、D两点,则图中阴影部分的面积是 cm2.
15.如图,⊙O与正六边形OABCDE的边OA、OE分别交于点F、G,则弧所对的圆周角∠FPG的大小为 度.
16.在半径为的圆中,60°的圆心角所对的弧长等于 。
三、计算题
17.如图,⊙O的直径AB平分弦CD, CD =10cm, AP: PB=1 : 5.求⊙O的半径.
18.如图,直径分别为CD、CE的两个半圆相切于点C,大半圆M的弦与小半圆N相切于点F,且AB∥CD,AB=4,设、的长分别为x、y,线段ED的长为z,则z(x+y)的值为 .
四、解答题
19.如图,在中,斜边,为的中点,的外接圆与交于点,过作的切线交的延长线于点.
(1)求证:;
(2)计算:的值.
20.如图,是的直径,是上的两点,且
(1)求证:
(2)若将四边形分成面积相等的两个三角形,试确定四边形的形状.
21.(1)已知:如图1,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.求证:DE=DF.
(2)如图2,已知△ABC内接于⊙O,AC是⊙O的直径,D是弧AB的中点,过点D作直线BC的垂线,分别交CB,CA的延长线于E,F,求证:EF是⊙O的切线.
22.已知: 如图, AB是⊙O的直径,⊙O过AC的中点D, DE切⊙O于点D, 交BC于点E.
(1)求证: DE⊥BC;
(2)如果CD=4,CE=3,求⊙O的半径.
23.如图,AC是⊙O的直径,弦BD交AC于点E.
(1)求证:△ADE∽△BCE;
(2)若AD2=AC·AE,求证:BC=CD.
24.如图,在同一平面内,有一组平行线l1、l2、l3,相邻两条平行线之间的距离均为4,点O在直线l1上,⊙O与直线l3的交点为A、B,AB=12,求⊙O的半径.
参考答案
1.C
2.C。
3.B
4.D
5.A
6.C
7.C
8.B
9.B
10.C
11.
12.45
13.7或17
14.
15.60。
16.2
17.连接CO,设圆的半径为r,
∵直径AB平分弦CD
∴AB垂直CD
∵AP:PB=1 : 5 ∴PO=r
∴r2=52+(r)2 得r=3
18.解:如图,过M作MG⊥AB于G,连MB,NF,
而AB=4,
∴BG=AG=2,
∴MB2﹣MG2=22=4,
又∵大半圆M的弦与小半圆N相切于点F,
∴NF⊥AB,
∵AB∥CD,
∴MG=NF,
设⊙M,⊙N的半径分别为R,r,
∴z(x+y)=(CD﹣CE)(π?R+π?r),
=(2R﹣2r)(R+r)?π,
=(R2﹣r2)?2π,
=4?2π,
=8π.
19.(1)证明:在中,为的中点,
为等边三角形.
点为的中心(内心,外心,垂心三心合一).
∴连接OA,OB,
又为的切线,
又四边形内接于圆
即
(2)解:由(1)知,为等边三角形.
则
又
20.(1)略(2)菱形
21.略
22.证明:(1)连结OD
∵DE切⊙O于点D
∴DE⊥OD, ∴∠ODE=900 又∵AD=DC, AO=OB
∴OD//BC
∴∠DEC=∠ODE=900, ∴DE⊥BC
(2)连结BD.
∵AB是⊙O的直径, ∴∠ADB=900
∴BD⊥AC, ∴∠BDC=900
又∵DE⊥BC, △RtCDB∽△RtCED
∴, ∴BC=
又∵OD=BC
∴OD=, 即⊙O的半径为
23.略
24.10
