山东省聊城市某重点高中2013届高三上学期1月份模块检测数学文试题
文档属性
| 名称 | 山东省聊城市某重点高中2013届高三上学期1月份模块检测数学文试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 179.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-22 00:00:00 | ||
图片预览




文档简介
山东省聊城市某重点高中2013届高三上学期1月份模块检测文科数学试题
考试时间:100分钟;
题号
一
二
三
总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
21世纪教育网
第I卷(选择题)
评卷人
得分
21世纪教育网
一、选择题
1.空间四边形ABCD中,若,则与所成角为( )
A. B. C. D.
2.若不等式组所表示的平面区域被直线分为面积相等的两部分,则的值是( )
A. B. C. D.
3.已知函数f(x)= 若a,b,c均不相等,且f(a)= f(b)= f(c),则abc的取值范围是( )
A.(1,10) B.(5,6) C.(10,12) D.(20,24) 21世纪教育网
4.已知p:函数有两个零点, q:,.若为真,为假,则实数m的取值范围为( )
A. B.
C. D.
5.已知数列,,,且,则数列的第五项为( )
A. B. C. D.
6.已知f满足f(ab)=f(a)+ f(b),且f(2)=,那么等于 ( )
A. B. C. D.
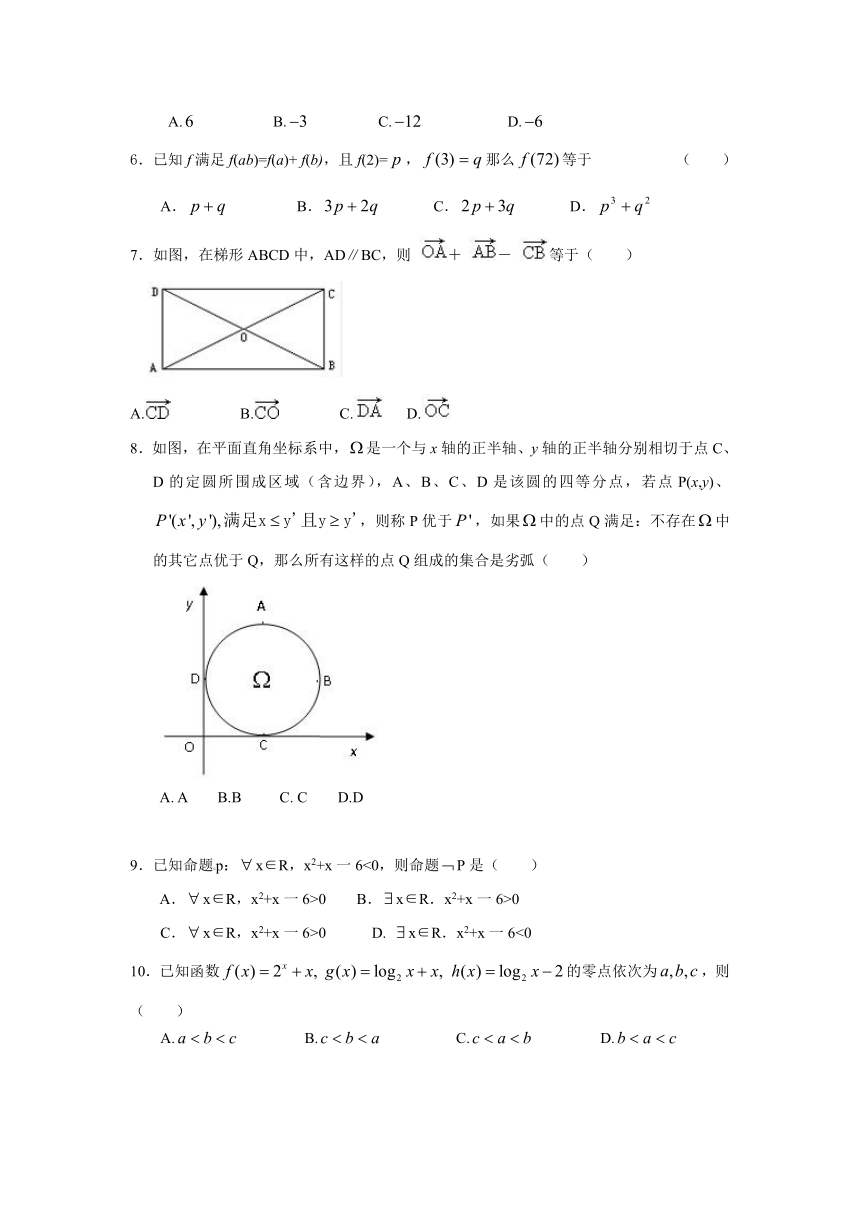
7.如图,在梯形ABCD中,AD∥BC,则 + - 等于( )
A. B. C. D.
8.如图,在平面直角坐标系中,是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域(含边界),A、B、C、D是该圆的四等分点,若点P(x,y)、,则称P优于,如果中的点Q满足:不存在中的其它点优于Q,那么所有这样的点Q组成的集合是劣弧( )
A. A B.B C. C D.D
9.已知命题p:x∈R,x2+x一6<0,则命题P是( )
A.x∈R,x2+x一6>0 B.x∈R.x2+x一6>0
C.x∈R,x2+x一6>0 D. x∈R.x2+x一6<0
10.已知函数的零点依次为,则( )
A. B. C. D.
11.已知,则=( )21世纪教育网
A、4 B、5 C、6 D、7
12.已知sinα=,则的值为( )
A.- B.- C. D.
21世纪教育网
第II卷(非选择题)
21世纪教育网
评卷人
得分
二、填空题
13.已知数列的首项为,且,则这个数列的通项公式为___________
14.若函数存在零点,则m的取值范围是__________.
15.已知是椭圆的一个焦点,是短轴的一个端点,线段的延长线交于点,且,则的离心率为 。
16.设a=sin(sin2008o),b=sin(cos2008o),c=cos(sin2008o),d=cos(cos2008°).则a,b,c,d从小到大的顺序是___________.
评卷人
得分
三、解答题
17.已知圆O:交x轴于A,B两点,曲线C是以AB为长轴,离心率为的椭圆,其左焦点为F.若P是圆O上一点,连结PF,过原点P作直线PF的垂线交直线于点Q.
(1)求椭圆C的标准方程;21世纪教育网
(2)若点P的坐标为(1,1),求证:直线PQ圆O相切;
(3)试探究:当点P在圆O上运动时(不与A、B重合),直线PQ与圆O是否保持相切的位置关系?若是,请证明;若不是,请说明理由.
18.已知等差数列中,,前10项的和21世纪教育网
(1)求数列的通项公式;
(2)若从数列中,依次取出第2、4、8,…,,…项,按原来的顺序排成一个新的数列,试求新数列的前项和.
19.已知数列是首项为且公比q不等于1的等比数列,是其前n项的和,成等差数列.
证明:成等比数列.
20.一家报刊推销员从报社买进报纸的价格是每份0.20元,卖出的价格是每份0.30元,卖不完的还可以以每份0.08元的价格退回报社.在一个月(以30天计算)有20天每天可卖出400份,其余10天只能卖250份,但每天从报社买进报纸的份数都相同,问应该从报社买多少份才能使每月所获得的利润最大?并计算每月最多能赚多少钱?
21.已知椭圆 经过点其离心率为.
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线与椭圆相交于A、B两点,以线段为邻边作平行四边形OAPB,其中顶点P在椭圆上,为坐标原点.求的取值范围.
22.将圆心角为1200,面积为3的扇形,作为圆锥的侧面,求圆锥的表面积和体积.
21世纪教育网
21世纪教育网
21世纪教育网
文科数学参考答案
一、选择题
1.D??????2.A??????
解析:不等式表示的平面区域如图所示阴影部分△ABC 由得A(1,1),又B(0,4),C(0,)21世纪教育网 ∴△ABC=,设与的 交点为D,则由知,∴ ∴选A。
3.C??????4.B??????5.D??????6.B??????7.D??????8.D??????
解析:依题意,在点Q组成的集合中任取一点,过该点分别作平行于两坐标轴的直线,构成的左上方区域(权且称为“第二象限”)与点Q组成的集合无公共元素,这样点Q组成的集合才为所求. 检验得:D.
9.B??????
解析:全称命题的否命题是特张命题,故选B
10.A??????11.C??????12.B??????
解析:===-
二、填空题
13.
14.
15.
16.bdc
三、解答题
17.解:(1)因为 则b=1,即椭圆C的标准方程为?? (2)因为P(1,1),所以 所以,所以直线OQ的方程为y= —2x. 21世纪教育网 又Q在直线上,所以点Q(—2,4)? 即PQ⊥OQ,故直线PQ与圆O相切,? (3)当点P在圆O上运动时,直线PQ与圆P保持相切的位置关系.? 设, 则 所以直线OQ的方程为 所以点Q?? 所以 所以,即OP⊥PQ(P不与A、B重合), 故直线PQ始终与圆O相切.
18.(1) ?? (2),则 ????????????????????????? = ????????????????????????? =
19.证明:由成等差数列,? 得, 即 ?? 变形得? 所以(舍去). 由? ? 得? ?? 所以成等比数列. 21世纪教育网
20.
? 数量(份)
价格(元)
金额(元)21世纪教育网
买进
30x
0.20
6x
卖出
20x+10*250
0.30
6x+750
退回
10(x-250)
0.08
0.8x-200
则每月获利润y=[(6x+750)+(0.8x-200)]-6x=0. 8x+550(250≤x≤400). y在x [250,400]上是一次函数. ∴x=400份时,y取得最大值870元. 答:每天从报社买进400份时,每月获的利润最大,最大利润为870元.
21.解:(Ⅰ)由已知可得,所以???? ① ?? 又点在椭圆上,所以??????????????? ② 由①②解之,得.??????????????????????????????? 故椭圆的方程为.???? ? (Ⅱ) 当时,在椭圆上,解得,所以. 当时,则由???? 消化简整理得:, ??? ③?? 设点的坐标分别为,则 .???? ?? 由于点在椭圆上,所以 .??? ?? 从而,化简得,经检验满足③式. ?? 又 ???????? ???????? ??? 因为,得,有, 故.????????????? ?????? 综上,所求的取值范围是.???? (Ⅱ)另解:设点的坐标分别为, 由在椭圆上,可得???? ①—②整理得? 由已知可得,所以?? 由已知当 ,即 ⑥?? 把④⑤⑥代入③整理得????? 与联立消整理得???? 由得, 所以 因为,得,有, 故.????????? 所求的取值范围是.21世纪教育网
22.=3,R=1;S=4;V=.
考试时间:100分钟;
题号
一
二
三
总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
21世纪教育网
第I卷(选择题)
评卷人
得分
21世纪教育网
一、选择题
1.空间四边形ABCD中,若,则与所成角为( )
A. B. C. D.
2.若不等式组所表示的平面区域被直线分为面积相等的两部分,则的值是( )
A. B. C. D.
3.已知函数f(x)= 若a,b,c均不相等,且f(a)= f(b)= f(c),则abc的取值范围是( )
A.(1,10) B.(5,6) C.(10,12) D.(20,24) 21世纪教育网
4.已知p:函数有两个零点, q:,.若为真,为假,则实数m的取值范围为( )
A. B.
C. D.
5.已知数列,,,且,则数列的第五项为( )
A. B. C. D.
6.已知f满足f(ab)=f(a)+ f(b),且f(2)=,那么等于 ( )
A. B. C. D.
7.如图,在梯形ABCD中,AD∥BC,则 + - 等于( )
A. B. C. D.
8.如图,在平面直角坐标系中,是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域(含边界),A、B、C、D是该圆的四等分点,若点P(x,y)、,则称P优于,如果中的点Q满足:不存在中的其它点优于Q,那么所有这样的点Q组成的集合是劣弧( )
A. A B.B C. C D.D
9.已知命题p:x∈R,x2+x一6<0,则命题P是( )
A.x∈R,x2+x一6>0 B.x∈R.x2+x一6>0
C.x∈R,x2+x一6>0 D. x∈R.x2+x一6<0
10.已知函数的零点依次为,则( )
A. B. C. D.
11.已知,则=( )21世纪教育网
A、4 B、5 C、6 D、7
12.已知sinα=,则的值为( )
A.- B.- C. D.
21世纪教育网
第II卷(非选择题)
21世纪教育网
评卷人
得分
二、填空题
13.已知数列的首项为,且,则这个数列的通项公式为___________
14.若函数存在零点,则m的取值范围是__________.
15.已知是椭圆的一个焦点,是短轴的一个端点,线段的延长线交于点,且,则的离心率为 。
16.设a=sin(sin2008o),b=sin(cos2008o),c=cos(sin2008o),d=cos(cos2008°).则a,b,c,d从小到大的顺序是___________.
评卷人
得分
三、解答题
17.已知圆O:交x轴于A,B两点,曲线C是以AB为长轴,离心率为的椭圆,其左焦点为F.若P是圆O上一点,连结PF,过原点P作直线PF的垂线交直线于点Q.
(1)求椭圆C的标准方程;21世纪教育网
(2)若点P的坐标为(1,1),求证:直线PQ圆O相切;
(3)试探究:当点P在圆O上运动时(不与A、B重合),直线PQ与圆O是否保持相切的位置关系?若是,请证明;若不是,请说明理由.
18.已知等差数列中,,前10项的和21世纪教育网
(1)求数列的通项公式;
(2)若从数列中,依次取出第2、4、8,…,,…项,按原来的顺序排成一个新的数列,试求新数列的前项和.
19.已知数列是首项为且公比q不等于1的等比数列,是其前n项的和,成等差数列.
证明:成等比数列.
20.一家报刊推销员从报社买进报纸的价格是每份0.20元,卖出的价格是每份0.30元,卖不完的还可以以每份0.08元的价格退回报社.在一个月(以30天计算)有20天每天可卖出400份,其余10天只能卖250份,但每天从报社买进报纸的份数都相同,问应该从报社买多少份才能使每月所获得的利润最大?并计算每月最多能赚多少钱?
21.已知椭圆 经过点其离心率为.
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线与椭圆相交于A、B两点,以线段为邻边作平行四边形OAPB,其中顶点P在椭圆上,为坐标原点.求的取值范围.
22.将圆心角为1200,面积为3的扇形,作为圆锥的侧面,求圆锥的表面积和体积.
21世纪教育网
21世纪教育网
21世纪教育网
文科数学参考答案
一、选择题
1.D??????2.A??????
解析:不等式表示的平面区域如图所示阴影部分△ABC 由得A(1,1),又B(0,4),C(0,)21世纪教育网 ∴△ABC=,设与的 交点为D,则由知,∴ ∴选A。
3.C??????4.B??????5.D??????6.B??????7.D??????8.D??????
解析:依题意,在点Q组成的集合中任取一点,过该点分别作平行于两坐标轴的直线,构成的左上方区域(权且称为“第二象限”)与点Q组成的集合无公共元素,这样点Q组成的集合才为所求. 检验得:D.
9.B??????
解析:全称命题的否命题是特张命题,故选B
10.A??????11.C??????12.B??????
解析:===-
二、填空题
13.
14.
15.
16.bdc
三、解答题
17.解:(1)因为 则b=1,即椭圆C的标准方程为?? (2)因为P(1,1),所以 所以,所以直线OQ的方程为y= —2x. 21世纪教育网 又Q在直线上,所以点Q(—2,4)? 即PQ⊥OQ,故直线PQ与圆O相切,? (3)当点P在圆O上运动时,直线PQ与圆P保持相切的位置关系.? 设, 则 所以直线OQ的方程为 所以点Q?? 所以 所以,即OP⊥PQ(P不与A、B重合), 故直线PQ始终与圆O相切.
18.(1) ?? (2),则 ????????????????????????? = ????????????????????????? =
19.证明:由成等差数列,? 得, 即 ?? 变形得? 所以(舍去). 由? ? 得? ?? 所以成等比数列. 21世纪教育网
20.
? 数量(份)
价格(元)
金额(元)21世纪教育网
买进
30x
0.20
6x
卖出
20x+10*250
0.30
6x+750
退回
10(x-250)
0.08
0.8x-200
则每月获利润y=[(6x+750)+(0.8x-200)]-6x=0. 8x+550(250≤x≤400). y在x [250,400]上是一次函数. ∴x=400份时,y取得最大值870元. 答:每天从报社买进400份时,每月获的利润最大,最大利润为870元.
21.解:(Ⅰ)由已知可得,所以???? ① ?? 又点在椭圆上,所以??????????????? ② 由①②解之,得.??????????????????????????????? 故椭圆的方程为.???? ? (Ⅱ) 当时,在椭圆上,解得,所以. 当时,则由???? 消化简整理得:, ??? ③?? 设点的坐标分别为,则 .???? ?? 由于点在椭圆上,所以 .??? ?? 从而,化简得,经检验满足③式. ?? 又 ???????? ???????? ??? 因为,得,有, 故.????????????? ?????? 综上,所求的取值范围是.???? (Ⅱ)另解:设点的坐标分别为, 由在椭圆上,可得???? ①—②整理得? 由已知可得,所以?? 由已知当 ,即 ⑥?? 把④⑤⑥代入③整理得????? 与联立消整理得???? 由得, 所以 因为,得,有, 故.????????? 所求的取值范围是.21世纪教育网
22.=3,R=1;S=4;V=.
同课章节目录
