苏科版八年级数学下册 17.4反比例函数 K的几何意义专题 课件 (共17张PPT)
文档属性
| 名称 | 苏科版八年级数学下册 17.4反比例函数 K的几何意义专题 课件 (共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 389.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 17:35:09 | ||
图片预览

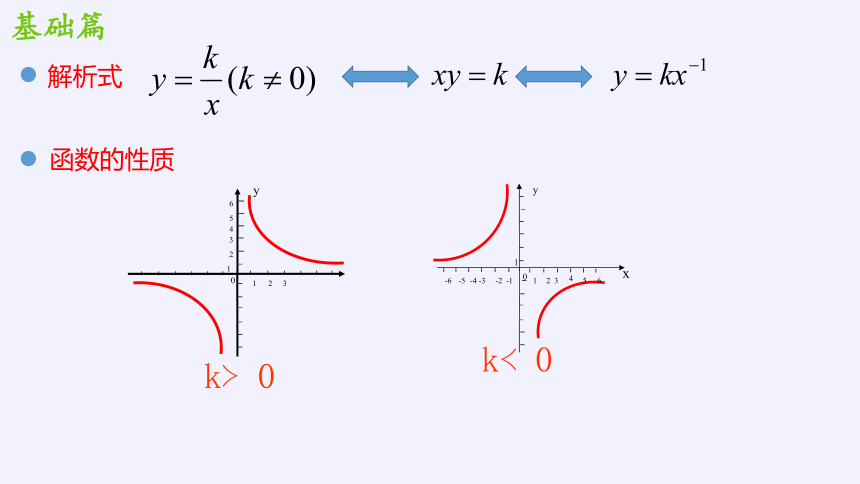




文档简介
(共17张PPT)
小结与思考
基础篇
解析式
y
0
1
2
3
1
2
3
4
5
6
-4
0
-5
1
-3
y
x
2
3
4
5
-1
6
-2
-6
1
k 0
k 0
函数的性质
基础篇
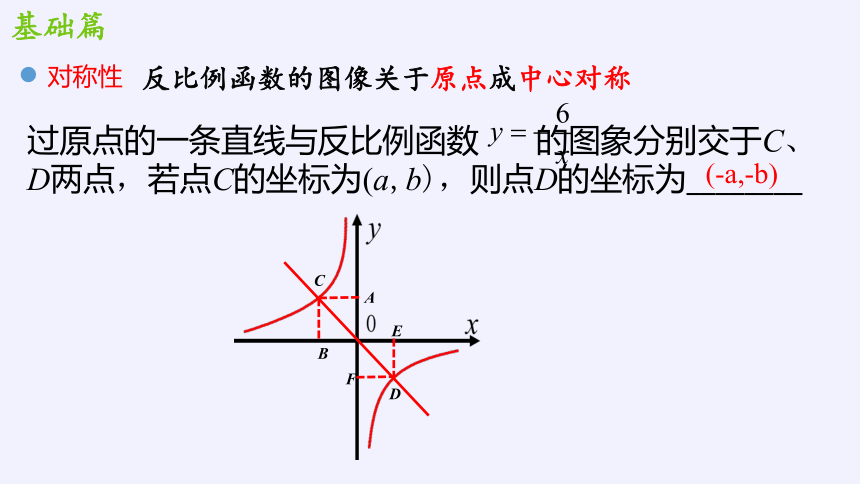
对称性
反比例函数的图像关于原点成中心对称
过原点的一条直线与反比例函数 的图象分别交于C、
D两点,若点C的坐标为(a,b),则点D的坐标为________
C
D
A
B
E
F
(-a,-b)
k的几何意义
基础篇
反比例函数 的图像上有一点E,过点 E 作
EP⊥ y 轴于点P,则△EOP的面积为________.
小试牛刀
变式:反比例函数 的图像上有一点E,过点E作EP⊥ y轴于点P,若在x轴上任意取一点F,则△EPF的面积为_________.
再显身手
已知点A、B分别在反比例函数 、
的图像上 ,AB∥x轴,则△ABO的面积是多少?
y
O
B
x
A
C
变式:已知点A、B分别在反比例函数 、
的图像上 ,AB∥x轴,点F在x轴上任意移动,则△ABF的面积是多少?
O
B
x
A
C
F
y
x
变式:平行四边形ABCD的顶点A在反比例函数 的图像上,AB∥x轴交y轴于点B,CD在x轴上任意移动,则四边形ABDC的面积是?
C’
例1:正比例函数 的图像与反比例函数 的图像交于A、B两点,过点A作AM⊥x轴,垂足为M,连接BM,求S△ABM
(a, )
(-a,- )
C
N
1.如图,已知反比例函数 、
,点P(1,1)在 上,PC⊥x 轴,
垂足为C,交 于点A,PD⊥y 轴,
垂足为D,交 于点B,求S△PAB
、
(1,1)
练习
变式:若点P为 在第一象限图像上任一点,求S△PAB
(a, )
2.已知反比例函数 ,点A(1,2)在图像上,过点A作AB⊥x轴
(1)求S△ABO
(2)点C(0,-2)在y轴上,
求S△ACO
(3)连接A、C和x轴交于点D,
求S△AOD
练习
C
D
(1,2)
-2
(4).若点C(2,1)在函数图像上,连接A、C和x轴交于点D,求S△AOD
C
D
(1,2)
(2,1)
3. 如图,过点E(1,4)的直线 分别交x轴、
y轴于点D、C,若直线与双曲线
的另一个交点是F(2,2);
(1)观察图像,直接说出当
时,x的值;
(2)求证:CE=DF;
(3)连接OE、OF,求S△OEF的面积.
拓展:如图,过点E(1,4)的直线 分别交x轴、
y轴于点D、C.若直线 与双曲线
的另一个交点是F点.
(1)过点E、F分别作x轴、y轴的平行
线,得到四边形OGAH,试探究四
边形OGAH的形状并说明理由.
(2)当四边形OGAH是正方形时,
求证:OE=OF.
(3).当k发生变化时,OCE和△OFD的面积有着怎样的数量关系?
谢 谢
小结与思考
基础篇
解析式
y
0
1
2
3
1
2
3
4
5
6
-4
0
-5
1
-3
y
x
2
3
4
5
-1
6
-2
-6
1
k 0
k 0
函数的性质
基础篇
对称性
反比例函数的图像关于原点成中心对称
过原点的一条直线与反比例函数 的图象分别交于C、
D两点,若点C的坐标为(a,b),则点D的坐标为________
C
D
A
B
E
F
(-a,-b)
k的几何意义
基础篇
反比例函数 的图像上有一点E,过点 E 作
EP⊥ y 轴于点P,则△EOP的面积为________.
小试牛刀
变式:反比例函数 的图像上有一点E,过点E作EP⊥ y轴于点P,若在x轴上任意取一点F,则△EPF的面积为_________.
再显身手
已知点A、B分别在反比例函数 、
的图像上 ,AB∥x轴,则△ABO的面积是多少?
y
O
B
x
A
C
变式:已知点A、B分别在反比例函数 、
的图像上 ,AB∥x轴,点F在x轴上任意移动,则△ABF的面积是多少?
O
B
x
A
C
F
y
x
变式:平行四边形ABCD的顶点A在反比例函数 的图像上,AB∥x轴交y轴于点B,CD在x轴上任意移动,则四边形ABDC的面积是?
C’
例1:正比例函数 的图像与反比例函数 的图像交于A、B两点,过点A作AM⊥x轴,垂足为M,连接BM,求S△ABM
(a, )
(-a,- )
C
N
1.如图,已知反比例函数 、
,点P(1,1)在 上,PC⊥x 轴,
垂足为C,交 于点A,PD⊥y 轴,
垂足为D,交 于点B,求S△PAB
、
(1,1)
练习
变式:若点P为 在第一象限图像上任一点,求S△PAB
(a, )
2.已知反比例函数 ,点A(1,2)在图像上,过点A作AB⊥x轴
(1)求S△ABO
(2)点C(0,-2)在y轴上,
求S△ACO
(3)连接A、C和x轴交于点D,
求S△AOD
练习
C
D
(1,2)
-2
(4).若点C(2,1)在函数图像上,连接A、C和x轴交于点D,求S△AOD
C
D
(1,2)
(2,1)
3. 如图,过点E(1,4)的直线 分别交x轴、
y轴于点D、C,若直线与双曲线
的另一个交点是F(2,2);
(1)观察图像,直接说出当
时,x的值;
(2)求证:CE=DF;
(3)连接OE、OF,求S△OEF的面积.
拓展:如图,过点E(1,4)的直线 分别交x轴、
y轴于点D、C.若直线 与双曲线
的另一个交点是F点.
(1)过点E、F分别作x轴、y轴的平行
线,得到四边形OGAH,试探究四
边形OGAH的形状并说明理由.
(2)当四边形OGAH是正方形时,
求证:OE=OF.
(3).当k发生变化时,OCE和△OFD的面积有着怎样的数量关系?
谢 谢
