沪科版数学八年级下册 第18章 勾股定理 单元综合能力测试(word版含解析)
文档属性
| 名称 | 沪科版数学八年级下册 第18章 勾股定理 单元综合能力测试(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 857.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 00:00:00 | ||
图片预览




文档简介
第18章 勾股定理 单元综合能力测试
一、单选题:本题共10个小题,每小题2分,共20分。在每小题给出的四个选项中只有一项是符合题目要求的。
1.(2022·山东槐荫·八年级期末)直角三角形的两直角边长分别为5和12,则斜边长为( )
A.13 B.14 C. D.1
2.(2022·全国·八年级期中)已知一个的两边长分别为3和4,则第三边长的平方是( )
A.25 B.14 C.7 D.7或25
3.(2021·江苏江阴·八年级期中)下列长度的三条线段能组成直角三角形的是( )
A.4,6,8 B.6,8,10 C.6,9,10 D.5,11,13
4.(2022·江苏江阴·八年级期末)已知,,分别是的三边,根据下列条件能判定为直角三角形的是( )
A.,, B.,,
C.,, D.,,
5.(2022·全国·八年级期末)已知三角形的三边长分别为a,b,c,且a+b=10,ab=18,c=8,则该三角形的形状是( )
A.等腰三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形
6.(2022·四川宜宾·八年级期末)已知RtABC中,∠ACB=90°,AC=BC,AB=4,D为BC的中点,E是线段AB上一点,连接CE、DE,则CE+DE的最小值是( )
A.2 B.2 C.4 D.2+2
7.(2022·广东·深圳市福田区第二实验学校八年级期中)如图,在底面半径为2,(π取3)高为8的圆柱体上有只小虫子在A点,它想爬到B点,则爬行的最短路程是( )
A.10 B.8 C.5 D.4
8.(2021·浙江·宁波市第七中学八年级期中)如果△ABC的三个顶点A,B,C所对的边分别为a,b,c.那么下列条件中能判断△ABC是直角三角形的是( )
A.∠A:∠B:∠C=3:4:5 B.∠A=25°,∠B=75°
C.a=,b=,c= D.a=6,b=10,c=12
9.(2021·全国·八年级单元测试)如图,在平面直角坐标系xOy中,已知点P(m,m),过点P作OP的垂线交函数(k>1)的图象于点Q.若Q的横坐标为1,且OP2﹣PQ2=6,则k的值为( )
A.2 B.3 C. D.4
10.(2021·江西九江·八年级期末)如图,在△ABC中,AB=6,AC=8,BC=10,△ABD,△ACE,△BCF都是等边三角形,下列结论中:①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=135°;④S四边形AEFD=20.正确的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题:本题共8个小题,每题3分,共24分。
11.(2021·全国·八年级单元测试)已知△ABC中,AB=17,AC=10,BC边上的高AD=8.则边BC的长为_______.
12.(2021·全国·八年级单元测试)已知等腰三角形的腰长是13cm,底边长10cm,则该等腰三角形的面积是_______cm2.
13.(2021·河南·郑州枫杨外国语学校八年级期中)如图,在△ABC中,点D是BC的中点,若AB=5,AC=13,AD=6,则BC的长为 ______.
14.(2021·浙江·温州市南浦实验中学八年级期中)如图,点D在△ABC内,∠BDC=90°,AB=3,AC=BD=2,CD=1,则图中阴影部分的面积为 _______________.
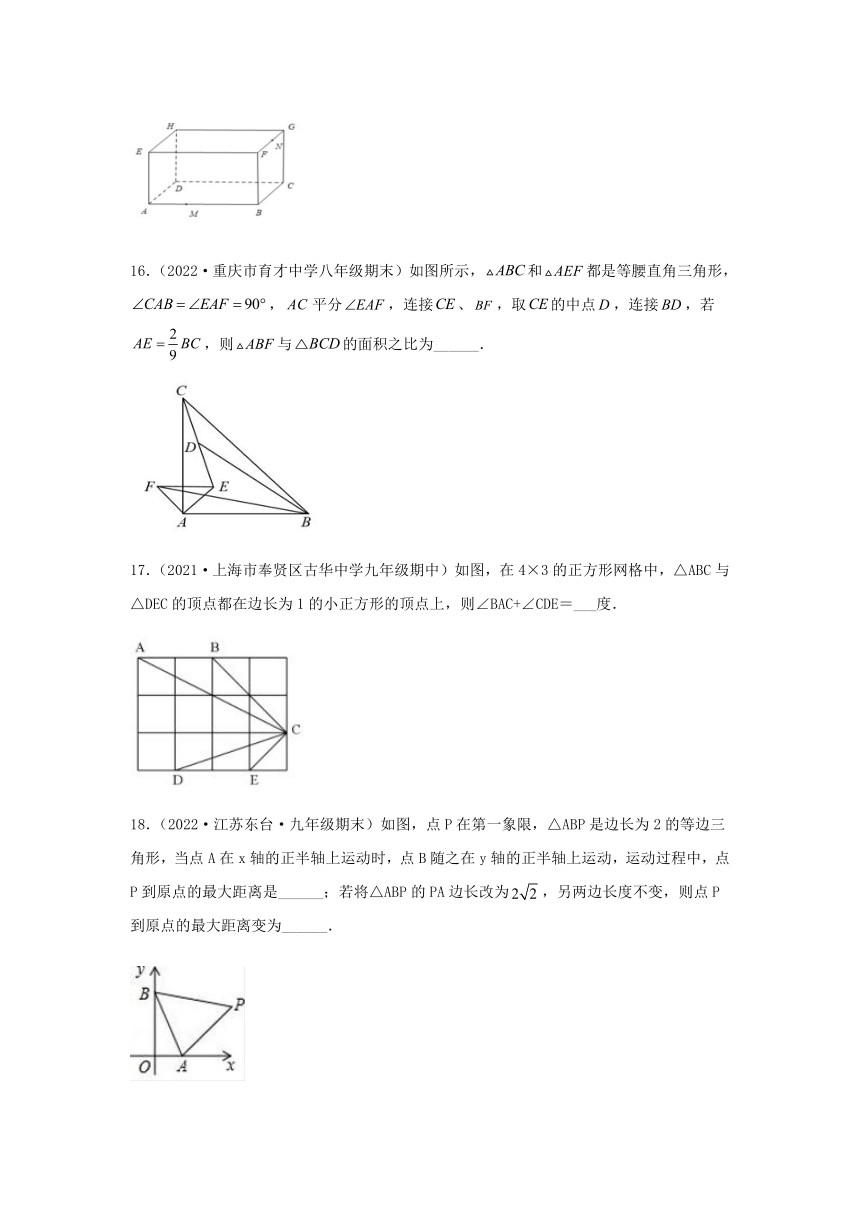
15.(2022·重庆黔江·八年级期末)如图是放在地面上的一个长方体盒子,其中,,,点在棱上,且,点是的中点,一只蚂蚁要沿着长方体盒子的表面从点爬行到点,它需要爬行的最短路程为______.
16.(2022·重庆市育才中学八年级期末)如图所示,和都是等腰直角三角形,,平分,连接、,取的中点,连接,若,则与的面积之比为______.
17.(2021·上海市奉贤区古华中学九年级期中)如图,在4×3的正方形网格中,△ABC与△DEC的顶点都在边长为1的小正方形的顶点上,则∠BAC+∠CDE=___度.
18.(2022·江苏东台·九年级期末)如图,点P在第一象限,△ABP是边长为2的等边三角形,当点A在x轴的正半轴上运动时,点B随之在y轴的正半轴上运动,运动过程中,点P到原点的最大距离是______;若将△ABP的PA边长改为,另两边长度不变,则点P到原点的最大距离变为______.
三、解答题:本题共7个小题,19-23每题7分,24小题9分,25每题12分,共56分。
19.(2021·全国·八年级单元测试)如图,中,D为边上一点,且.
(1)求证:;
(2)若,,求的长.
20.(2021·全国·八年级单元测试)如图,红星村A和幸福村B在一条小河的同侧,它们到河岸的距离,分别为1和3,又知道的长为3,现要在河岸上建一水厂向两村输送自来水,铺设水管的工程费用为每千米20000元.
(1)请在上选择水厂位置,使铺设水管的费用最省(作图工具不限,保留作图痕迹);
(2)求铺设水管的最省总费用.
21.(2021·广东·珠海市文园中学八年级期中)如图,两个全等的等边三角形△ABC与△ACD,边长为6,高为a,在拼成的四边形ABCD中,点E、F分别为AB、AD边上的动点,满足BE=AF,连接EF,CE,CF.
(1)求证:△CEF是等边三角形;
(2)△AEF周长的最小值是 .(用含a的式子表示)
22.(2021·全国·八年级单元测试)如图,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条路CH,测得CB=1.5千米,CH=1.2千米,HB=0.9千米.
(1)问CH是否为从村庄C到河边的最近路?请通过计算加以说明;
(2)求新路CH比原路CA少多少千米?
23.(2021·全国·八年级单元测试)课间,小明拿着王老师的等腰直角三角板玩,三角板不小心掉到墙缝中.我们知道两堵墙都是与地面垂直的,如图.王老师没有批评他,但要求他完成如下两个问题:
(1)试说明;
(2)从三角板的刻度知AC=25cm,算算一块砖的厚度.(每块砖的厚度均相等)小明先将问题所给条件做了如下整理:如图,中,CA=CB,∠ACB=90°,AD⊥DE于D,BE⊥DE于E.请你帮他完成上述问题.
24.(2021·江苏·苏州工业园区星湾学校八年级期中)如图,在网格中,每个小正方形的边长都为1.
(1)的面积为________;
(2)判断的形状,并说明理由.
(3)求边上的高.
25.(2022·湖南广益实验中学八年级期末)我们规定,三角形任意两边的“广益值”等于第三边上的中线和这边一半的平方差.如图1,在中,是边上的中线,与的“广益值”就等于的值,可记为
(1)在中,若,,求的值.
(2)如图2,在中,,,求,的值.
(3)如图3,在中,是边上的中线,,,,求和的长.
第18章 勾股定理 单元综合能力测试
单选题:本题共10个小题,每小题2分,共20分。在每小题给出的四个选项中只有一项是符合题目要求的。
1.(2022·山东槐荫·八年级期末)直角三角形的两直角边长分别为5和12,则斜边长为( )
A.13 B.14 C. D.1
【答案】A
【分析】根据勾股定理,即可求得斜边长.
【详解】解:由题意得,该直角三角形的斜边长为:
故选:A.
【点睛】此题主要考查勾股定理,熟练掌握勾股定理即可解题.
2.(2022·全国·八年级期中)已知一个的两边长分别为3和4,则第三边长的平方是( )
A.25 B.14 C.7 D.7或25
【答案】D
【分析】由于4是三角形的直角边与斜边不能确定,故应分两种情况进行讨论.
【详解】解:由于4是三角形的直角边与斜边不能确定,故应分两种情况进行讨论:
(1)3、4都为直角边,由勾股定理得,斜边为5;
(2)3为直角边,4为斜边,由勾股定理得,直角边为.
∴第三边长的平方是25或7,
故选:D.
【点睛】本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.
3.(2021·江苏江阴·八年级期中)下列长度的三条线段能组成直角三角形的是( )
A.4,6,8 B.6,8,10 C.6,9,10 D.5,11,13
【答案】B
【分析】根据勾股定理的逆定理:两边的平方和等于第三边的平方,即可完成解答.
【详解】解:A、,故不能组成直角三角形;B、,故能组成直角三角形;C、,故不能组成直角三角形;D、,故不能组成直角三角形;
故选:B
【点睛】本题考查了勾股定理的逆定理,熟练掌握此定理是关键.
4.(2022·江苏江阴·八年级期末)已知,,分别是的三边,根据下列条件能判定为直角三角形的是( )
A.,, B.,,
C.,, D.,,
【答案】B
【分析】根据勾股定理的逆定理对四个选项进行逐一判断即可.
【详解】解:A、∵22+32≠42,∴不能构成直角三角形,故本选项错误;B、∵52+122=132,∴能构成直角三角形,故本选项正确;C、∵62+82≠122,∴能构成直角三角形,故本选项错误;D、∵62+122≠152,∴不能构成直角三角形,故本选项错误.
故选:B.
【点睛】本题考查的是勾股定理的逆定理,即如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.
5.(2022·全国·八年级期末)已知三角形的三边长分别为a,b,c,且a+b=10,ab=18,c=8,则该三角形的形状是( )
A.等腰三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形
【答案】B
【分析】根据完全平方公式利用a+b=10,ab=18求出,即可得到三角形的形状.
【详解】解:∵a+b=10,ab=18,
∴=(a+b)2-2ab=100-36=64,
∵,c=8,
∴=64,
∴=,
∴该三角形是直角三角形,
故选:B.
【点睛】此题考查勾股定理的逆定理,完全平方公式,能够利用完全平方公式由已知条件求出是解题的关键.
6.(2022·四川宜宾·八年级期末)已知RtABC中,∠ACB=90°,AC=BC,AB=4,D为BC的中点,E是线段AB上一点,连接CE、DE,则CE+DE的最小值是( )
A.2 B.2 C.4 D.2+2
【答案】B
【分析】作点C关于AB的对称点,连接,与AB交于点E,作DF于点F,则CE=,CE+DE= +DE,线段即为CE+DE得最小值.
【详解】解:如图,作点C关于AB的对称点,连接,与AB交于点E,作DF于点F,
则CE=,CE+DE= +DE,线段即为CE+DE得最小值.
∠ACB=90°,AC=BC,AB=4,
D为BC的中点,
CD=BD=BC=×4=2
CF=DF=,CC'=2CG=2×=
故选:B.
【点睛】此题考查了线路最短的问题,勾股定理,确定动点E何位置时,使DE+CE的值最小是解题的关键.
7.(2022·广东·深圳市福田区第二实验学校八年级期中)如图,在底面半径为2,(π取3)高为8的圆柱体上有只小虫子在A点,它想爬到B点,则爬行的最短路程是( )
A.10 B.8 C.5 D.4
【答案】A
【分析】若蚂蚁从侧表面从A爬行到B,首先将此圆柱展成平面图,根据两点间线段最短,可得AB最短,由勾股定理即可求得需要爬行的最短路程.
【详解】解:若蚂蚁从侧表面从A爬行到B,将此圆柱展成平面图得:
∵圆柱的高等于8,底面半径为2(π=3),
∴AC=8,BC==4π=6,
∴AB=10.
根据两点之间线段最短,蚂蚁从侧表面从A爬行到B最短路径为10.
故选:A.
【点睛】本题主要考查了平面展开图求最短路径问题,将圆柱体展开,根据两点之间线段最短,运用勾股定理解答是解题关键.
8.(2021·浙江·宁波市第七中学八年级期中)如果△ABC的三个顶点A,B,C所对的边分别为a,b,c.那么下列条件中能判断△ABC是直角三角形的是( )
A.∠A:∠B:∠C=3:4:5 B.∠A=25°,∠B=75°
C.a=,b=,c= D.a=6,b=10,c=12
【答案】C
【分析】根据三角形内角和定理得出,再根据求出最大角,再根据直角三角形的判定即可判断选项;根据三角形的内角和定理求出,即可判断选项;根据勾股定理的逆定理即可判断选项、选项.
【详解】解:.,,
最大角,
不是直角三角形,故本选项不符合题意;
.,,
,
不是直角三角形,故本选项不符合题意;
.,,,
,
是直角三角形,故本选项符合题意;
.,,,
,
不是直角三角形,故本选项不符合题意;
故选:C.
【点睛】本题考查了三角形内角和定理和勾股定理的逆定理,解题的关键是能熟记勾股定理的逆定理和三角形内角和等于180°.
9.(2021·全国·八年级单元测试)如图,在平面直角坐标系xOy中,已知点P(m,m),过点P作OP的垂线交函数(k>1)的图象于点Q.若Q的横坐标为1,且OP2﹣PQ2=6,则k的值为( )
A.2 B.3 C. D.4
【答案】B
【分析】根据点P(m,m)可得均为等腰直角三角形,根据OP2﹣PQ2=6得出,求出m值即可求得k的值.
【详解】解:作,,
P(m,m),
,
,
,
均为等腰直角三角形,
,
,
,
即,
解得:,
,
点的纵坐标为,
,
将点Q代入中,
得:,
故选:B.
【点睛】本题主要考查一次函数函数图像,等腰三角形以及勾股定理,根据已知条件求出m的值是解题的关键.
10.(2021·江西九江·八年级期末)如图,在△ABC中,AB=6,AC=8,BC=10,△ABD,△ACE,△BCF都是等边三角形,下列结论中:①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=135°;④S四边形AEFD=20.正确的个数是( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【分析】由,得出,故①正确;再由证得,得,同理,得,则四边形是平行四边形,故②正确;然后由平行四边形的性质得,则③错误;最后求出,故④错误;即可得出答案.
【详解】解:,,,,
,
是直角三角形,,
,故①正确;
,都是等边三角形,
,
,
和都是等边三角形,
,,,
,
在与中,
,
,
,
同理可证:,
,
四边形是平行四边形,故②正确;
,故③错误;
过作于,如图所示:
则,
四边形是平行四边形,
,
,
,故④错误;
正确的个数是2个,
故选:B.
【点睛】本题考查了平行四边形的判定与性质、勾股定理的逆定理、全等三角形的判定与性质、等边三角形的性质、含角的直角三角形的性质等知识;熟练掌握平行四边形的判定与性质,证明是解题的关键.
二、填空题:本题共8个小题,每题3分,共24分。
11.(2021·全国·八年级单元测试)已知△ABC中,AB=17,AC=10,BC边上的高AD=8.则边BC的长为_______.
【答案】21或9
【分析】根据题意,可能是锐角三角形或者钝角三角形,分两种情况进行讨论作图,然后利用勾股定理即可求解.
【详解】解:在中,,,BC边上高,
如图所示,当为锐角三角形时,
在中,,由勾股定理得:
,
∴,
在中,,由勾股定理得:
,
∴,
∴BC的长为:;
如图所示:当为钝角三角形时,
在中,,由勾股定理得:
,
∴,
在中,,由勾股定理得:
,
∴,
∴BC的长为:;
综上可得:BC的长为:21或9.
故答案为:21或9.
【点睛】题目主要考查勾股定理,进行分类讨论作出图象运用勾股定理解直角三角形是解题关键.
12.(2021·全国·八年级单元测试)已知等腰三角形的腰长是13cm,底边长10cm,则该等腰三角形的面积是_______cm2.
【答案】60
【分析】根据等腰三角形三线合一定理和勾股定理即可求得底边的高,从而求得三角形面积.
【详解】解:如图所示:AB=AC=13cm,BC=10cm
作AD⊥BC于D,则∠ADB=90°
∴,
∴,
∴△ABC的面积=,
故答案为:60.
【点睛】本题考查勾股定理和等腰三角形的性质,掌握等腰三角形三线合一是解题关键.
13.(2021·河南·郑州枫杨外国语学校八年级期中)如图,在△ABC中,点D是BC的中点,若AB=5,AC=13,AD=6,则BC的长为 ______.
【答案】
【分析】延长AD到E,使DE=AD,连接BE.先运用SAS证明△ADC≌△EDB,得出BE=13.再由勾股定理的逆定理证明出∠BAE=90°,然后在△ABD中运用勾股定理求出BD的长,从而得出BC=2BD.
【详解】解:延长AD到E,使DE=AD,连接BE.
在△ADC与△EDB中,
,
∴△ADC≌△EDB(SAS),
∴AC=BE=13.
在△ABE中,AB=5,AE=12,BE=13,
∴AB2+AE2=BE2,
∴∠BAE=90°.
在△ABD中,∠BAD=90°,AB=5,AD=6,
∴BD=,
∴BC=.
故答案为:.
【点睛】本题考查了全等三角形的判定与性质,勾股定理及其逆定理,综合性较强,难度中等.题中延长中线的一倍是常用的辅助线的作法.
14.(2021·浙江·温州市南浦实验中学八年级期中)如图,点D在△ABC内,∠BDC=90°,AB=3,AC=BD=2,CD=1,则图中阴影部分的面积为 _______________.
【答案】##
【分析】根据勾股定理和,,,可以先求出的长,然后根据勾股定理的逆定理可以判断的形状,从而可以求出阴影部分的面积.
【详解】解:,,,
,
,,
,
是直角三角形,,
阴影,
故答案为:.
【点睛】本题考查勾股定理的逆定理、勾股定理、三角形的面积,解题的关键是求出的长.
15.(2022·重庆黔江·八年级期末)如图是放在地面上的一个长方体盒子,其中,,,点在棱上,且,点是的中点,一只蚂蚁要沿着长方体盒子的表面从点爬行到点,它需要爬行的最短路程为______.
【答案】10
【分析】利用平面展开图有两种情况,画出图形利用勾股定理求出MN的长即可.
【详解】解:如图,
∵AB=9,BC=GF=6,BF=5,点是的中点,
∴BM=9-3=6,BN=5+3=8,
∴
如图2,
∵AB=8,BC=GF=6,BF=5,
∴PM=9-3+3=9,NP=5,
∴.
∵因为,所以蚂蚁沿长方体表面从点爬行到点的最短距离的10
故答案为:10
【点睛】此题主要考查了平面展开图的最短路径问题和勾股定理的应用,利用展开图有两种情况分析得出是解题关键.
16.(2022·重庆市育才中学八年级期末)如图所示,和都是等腰直角三角形,,平分,连接、,取的中点,连接,若,则与的面积之比为______.
【答案】4:5
【分析】延长AE交BC于点G,连接BE,过点F作交BA的延长线于点H,根据等腰直角三角形的性质及角平分线的计算可得,AG平分,利用等腰三角形“三线合一”性质得出且,设,则,由勾股定理及线段间的数量关系得出,,计算出的面积,结合图形及题意可得,根据等角对等边得出为等腰直角三角形,利用勾股定理可得,结合图形计算的面积,最后求面积比即可.
【详解】解:如图所示:延长AE交BC于点G,连接BE,过点F作交BA的延长线于点H,
∵与均为等腰直角三角形,
∴,,,
∵AC平分,
∴,
∴,
∴AG平分,
∴且,
∵,
∴,
设,则,
∴,
∵,,
∴,
∴,
∴,
∵,
∴,
∴,
∵D为CE中点,
∴,
∵与中,CD边和DE边上的高相等,都是点B到直线CE的距离,
∴,
∵,
∴,
∵,
∴,
∵,
∴,,
∴为等腰直角三角形,
∴,
∴,
∴,
∴,
故答案为:.
【点睛】题目主要考查角平分线计算,勾股定理,等腰三角形的判定和性质等,理解题意,结合图形,作出辅助线,综合运用这些知识点是解题关键.
17.(2021·上海市奉贤区古华中学九年级期中)如图,在4×3的正方形网格中,△ABC与△DEC的顶点都在边长为1的小正方形的顶点上,则∠BAC+∠CDE=___度.
【答案】
【分析】连接、,根据勾股定理以及勾股定理的逆定理求解即可.
【详解】解:连接、,如下图:
由勾股定理得,,,
,,
∵,,
∴,,
∴为等腰直角三角形,为直角三角形,
∴
∴
故答案为:
【点睛】此题考查了勾股定理以及勾股定理的逆定理,解题的关键是熟练掌握勾股定理以及勾股定理的逆定理.
18.(2022·江苏东台·九年级期末)如图,点P在第一象限,△ABP是边长为2的等边三角形,当点A在x轴的正半轴上运动时,点B随之在y轴的正半轴上运动,运动过程中,点P到原点的最大距离是______;若将△ABP的PA边长改为,另两边长度不变,则点P到原点的最大距离变为______.
【答案】 1+ 1+
【详解】解:根据当O到AB的距离最大时,OP的值最大,得到O到AB的最大值是AB=1,此时在斜边的中点M上,由勾股定理求出PM,即可求出答案;将△ABP的PA边长改为,另两边长度不变,根据,得到∠PBA=90°,由勾股定理求出PM即可.
详解:取AB的中点M,连OM,PM,
在Rt△ABO中,OM==1,在等边三角形ABP中,PM=,
无论△ABP如何运动,OM和PM的大小不变,当OM,PM在一直线上时,P距O最远,
∵O到AB的最大值是AB=1,此时在斜边的中点M上, 由勾股定理得:PM=,
∴OP=1+,
将△AOP的PA边长改为,另两边长度不变, ∵,
∴∠PBA=90°,由勾股定理得:PM=, ∴此时OP=OM+PM=1+.
点睛:本题主要考查对直角三角形斜边上的中线性质,坐标与图形性质,三角形的三边关系,勾股定理的逆定理等边三角形的性质等知识点的理解和掌握,能根据理解题意求出PD的值是解此题的关键.
三、解答题:本题共7个小题,19-23每题7分,24小题9分,25每题12分,共56分。
19.(2021·全国·八年级单元测试)如图,中,D为边上一点,且.
(1)求证:;
(2)若,,求的长.
【答案】(1)见详解;(2)8
【分析】
(1)根据∠ACB=90°,,推出∠B=∠DCB,得出CD=BD,再根据,得出CD=AD,从而得出AD=BD;
(2)根据(1)先求出AB的长,再根据勾股定理即可求出AC的长.
【详解】解:(1)∵∠ACB=90°,
∴∠A+∠B=90°,∠DCA+∠DCB=90°,
∵,
∴∠B=∠DCB,
∴CD=BD,
∵,
∴CD=AD,
∴AD=BD;
(2)由(1)得:AD=CD=BD,
∵CD=5,
∴AB=10,
∵BC=6,∠ACB=90°,
∴AC=.
【点睛】此题考查了勾股定理,等腰三角形的判定定理,根据在三角形中,等角等边对求出CD=AD=DB是解题的关键.
20.(2021·全国·八年级单元测试)如图,红星村A和幸福村B在一条小河的同侧,它们到河岸的距离,分别为1和3,又知道的长为3,现要在河岸上建一水厂向两村输送自来水,铺设水管的工程费用为每千米20000元.
(1)请在上选择水厂位置,使铺设水管的费用最省(作图工具不限,保留作图痕迹);
(2)求铺设水管的最省总费用.
【答案】(1)见解析;(2)100000元.
【分析】
(1)延长AC到F,使CF=AC,连接BF,交CD于E,则E为所求;
(2)过B作BN⊥CA,交CA的延长线于N,求出BN,NC长,根据勾股定理求出BF,即可得出答案.
【详解】解:(1)延长AC到F,使CF=AC,连接BF,交CD于E,
∵AC⊥CD,
∴AE=FE,
∴AE+BE=FE+BE=BF,
则在CD上选择水厂位置是E时,使铺设管道的费用最省;
(2)如上图,过B作BN⊥CA,交CA的延长线于N,
∴BN=CD=3km,CN=BD=3km,
∵AC=CF=1km,
∴NF=4km,
在Rt△BNF中,由勾股定理得:BF=km,
∵AC⊥CD,AC=CF,
∴AE=FE,
∴AE+BE=EF+BE=BF=5km,
∴铺设水管的最最省总费用是:20000×5=100000(元).
【点睛】本题考查了线段垂直平分线的性质及勾股定理,掌握线段垂直平分线的性质及勾股定理等知识是解题的关键,此类题目重点培养学生的动手操作能力和计算能力.
21.(2021·广东·珠海市文园中学八年级期中)如图,两个全等的等边三角形△ABC与△ACD,边长为6,高为a,在拼成的四边形ABCD中,点E、F分别为AB、AD边上的动点,满足BE=AF,连接EF,CE,CF.
(1)求证:△CEF是等边三角形;
(2)△AEF周长的最小值是 .(用含a的式子表示)
【答案】(1)证明见解析;(2)6+3
【分析】
(1)证明△BEC≌△AFC(SAS),可得结论;
(2)△AEF的周长=AE+AF+EF=AE+BE+EF=AB+EF=6+EF,推出EF的值最小时,△AEF的周长最小,因为△ECF是等边三角形,推出EF=CE,推出当CE⊥AB时,CE的值最小.
【详解】解:(1)证明:∵△ABC,△ACD是全等的等边三角形,
∴AC=BC,∠ABC=∠DAC=∠BCA=60°,
∵AF=BE,在△CBE和△CAF中,
,
∴△BEC≌△AFC(SAS),
∴CE=CF,∠BCE=∠ACF,
∴∠BCE+∠ACE=∠ACF+∠ACE,
∴∠ECF=∠BCA=60°,
∴△CEF是等边三角形.
(2)
解:∵△AEF的周长=AE+AF+EF=AE+BE+EF=AB+EF=6+EF,
∴EF的值最小时,△AEF的周长最小,
∵△ECF是等边三角形,
∴EF=CE,
∴当CE⊥AB时,CE的值最小,
∵△ABC是等边三角形,且CE⊥AB,
∴,
在Rt△AEC中,CE==3,
∴△AEF的周长的最小值为6+3,
故答案为:6+3.
【点睛】本题属于三角形综合题,考查了等边三角形的性质,全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考压轴题.
22.(2021·全国·八年级单元测试)如图,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条路CH,测得CB=1.5千米,CH=1.2千米,HB=0.9千米.
(1)问CH是否为从村庄C到河边的最近路?请通过计算加以说明;
(2)求新路CH比原路CA少多少千米?
【答案】解:(1)是,理由见详解; (2)新路CH比原路CA少0.05千米.
【分析】
(1)根据勾股定理的逆定理验证△CHB为直角三角形,进而得到CH⊥AB,再根据点到直线的距离垂线段最短即可解答;
(2)在△ACH中根据勾股定理解答即可.
【详解】解:(1)是,理由如下:
在△CHB中,
∵CH2+BH2=1.22+0.92=2.25=1.52=BC2,
即CH2+BH2=BC2,
∴△CHB为直角三角形,且∠CHB=90°,
∴CH⊥AB,
由点到直线的距离垂线段最短可知,CH是从村庄C到河边AB的最近路;
(2)设AC=x千米,
在Rt△ACH中,由已知设AC=x,AH=x-0.9,CH=1.2,
由勾股定理得:AC2=AH2+CH2
∴x2=(x-0.9)2+1.22,
解得x=1.25,即AC=1.25,
故AC-CH=1.25-1.2=0.05(千米)
答:新路CH比原路CA少0.05千米.
【点睛】本题考查勾股定理及勾股定理的逆定理的应用,熟练掌握勾股定理及逆定理是解决本题的关键.
23.(2021·全国·八年级单元测试)课间,小明拿着王老师的等腰直角三角板玩,三角板不小心掉到墙缝中.我们知道两堵墙都是与地面垂直的,如图.王老师没有批评他,但要求他完成如下两个问题:
(1)试说明;
(2)从三角板的刻度知AC=25cm,算算一块砖的厚度.(每块砖的厚度均相等)小明先将问题所给条件做了如下整理:如图,中,CA=CB,∠ACB=90°,AD⊥DE于D,BE⊥DE于E.请你帮他完成上述问题.
【答案】(1)证明见解析;(2)5cm
【分析】
(1)根据题意可得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,进而得到∠ADC=∠CEB=90°,再根据等角的余角相等可得∠BCE=∠DAC,再证明△ADC≌△CEB即可.
(2)利用(1)中全等三角形的性质进行解答.
【详解】解:证明:(1)如图:
∵AD⊥DE,BE⊥DE,
∴∠ADC=∠BEC=90°,
∴∠1+∠2=90°,
∵∠ACB=90°,
∴∠2+∠3=180°﹣90°=90°,
∵∠ADC=∠BEC=90°,
∴∠1=∠3,
由∠ADC=∠BEC=90°,∠1=∠3,CA=CB,
∴△ADC≌△CEB;
(2)设每块砖厚度为xcm,由①得,DC=BE=3xcm,AD=4xcm,
∵∠ADC=90°,
∴AD2+CD2=AC2,
即(4x)2+(3x)2=252,解得x=5,(x=﹣5舍去),
∴每块砖厚度为5cm.
【点睛】此题主要考查了全等三角形的应用,关键是正确找出证明三角形全等的条件.
24.(2021·江苏·苏州工业园区星湾学校八年级期中)如图,在网格中,每个小正方形的边长都为1.
(1)的面积为________;
(2)判断的形状,并说明理由.
(3)求边上的高.
【答案】(1)5;(2)△ABC是直角三角形,理由见解析;(3)2.
【分析】
(1)根据割补法即可求解;
(2)利用勾股定理的逆定理即可判断是直角三角形;
(3)过点C作CF⊥AB于点F,根据等积法即可求得CF值.
(1)
解:如图:
∵AE=1,BD=4,ED=4,EC=DC=2,
∴S△ABC=S梯形ABDE-S△BCD-S△ACE=
=
=
=10-4-1
=5,
故答案为:5;
(2)
解:△ABC是直角三角形,理由如下:
∵AB2=32+42=25,BC2=42+22=20,AC2=12+22=5,
∴BC2 +AC2=20+5=25,
即AB2= BC2 +AC2,
故△ABC是直角三角形.
(3)
解:如图:过点C作CF⊥AB于点F,
由(1)(2)知:S△ABC=5,AB=5,
∴S△ABC=,
即,
解得CF=2,
故边上的高为2.
【点睛】此题考查三角形面积,勾股定理及其逆定理,掌握基本知识是解答此题的关键.
25.(2022·湖南广益实验中学八年级期末)我们规定,三角形任意两边的“广益值”等于第三边上的中线和这边一半的平方差.如图1,在中,是边上的中线,与的“广益值”就等于的值,可记为
(1)在中,若,,求的值.
(2)如图2,在中,,,求,的值.
(3)如图3,在中,是边上的中线,,,,求和的长.
【答案】(1)AC=9;(2)ABAC=-72,BABC=216;(3)BC=2OC=2,AB=10.
【分析】
(1)在Rt中,根据勾股定理和新定义可得AO2-OC2=81=AC2;
(2)①先利用含30°的直角三角形的性质求出AO=2,OB=,再用新定义即可得出结论;
②先构造直角三角形求出BE,AE,再用勾股定理求出BD,最后用新定义即可得出结论;
(3)作BD⊥CD,构造直角三角形BCD,根据三角形面积关系求出BD,根据新定义和勾股定理逆定理得出三角形AOD是直角三角形,根据中线性质得出OA的长度,根据勾股定理求出OC,从而得出BC,再根据勾股定理求出CD,再求出AD,再运用勾股定理求出AB.
【详解】解:(1)已知如图:AO为BC上的中线,
在Rt中,
AO2-OC2=AC2
因为
所以AO2-OC2=81
所以AC2=81
所以AC=9.
(2)①如图2,取BC的中点D,连接AO,∵AB=AC,∴AO⊥BC,
在△ABC中,AB=AC,∠BAC=120°,∴∠ABC=30°,
在Rt△AOB中,AB=12,∠ABC=30°,∴AO=6,OB==,
∴ABAC=AO2﹣BO2=36﹣108=﹣72,
②取AC的中点D,连接BD,∴AD=CD=AC=6,过点B作BE⊥AC交CA的延长线于E,在Rt△ABE中,∠BAE=180°﹣∠BAC=60°,∴∠ABE=30°,
∵AB=12,∴AE=6,BE=,
∴DE=AD+AE=12,
在Rt△BED中,根据勾股定理得,BD=
∴BABC=BD2﹣CD2=216;
(3)作BD⊥CD,
因为,,
所以BD=2,
因为,是边上的中线,
所以AO2-OC2=-64,
所以OC2-AO2=64,
由因为AC2=82=64,
所以OC2-AO2= AC2
所以∠OAC=90°
所以OA=
所以OC=
所以BC=2OC=2,
在Rt△BCD中,
CD=
所以AD=CD-AC=16-8=8
所以AB=
【点睛】考核知识点:勾股定理逆定理,含30°直角三角形性质.借助辅助线构造直角三角形,运用勾股定理等直角三角形性质解决问题是关键
一、单选题:本题共10个小题,每小题2分,共20分。在每小题给出的四个选项中只有一项是符合题目要求的。
1.(2022·山东槐荫·八年级期末)直角三角形的两直角边长分别为5和12,则斜边长为( )
A.13 B.14 C. D.1
2.(2022·全国·八年级期中)已知一个的两边长分别为3和4,则第三边长的平方是( )
A.25 B.14 C.7 D.7或25
3.(2021·江苏江阴·八年级期中)下列长度的三条线段能组成直角三角形的是( )
A.4,6,8 B.6,8,10 C.6,9,10 D.5,11,13
4.(2022·江苏江阴·八年级期末)已知,,分别是的三边,根据下列条件能判定为直角三角形的是( )
A.,, B.,,
C.,, D.,,
5.(2022·全国·八年级期末)已知三角形的三边长分别为a,b,c,且a+b=10,ab=18,c=8,则该三角形的形状是( )
A.等腰三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形
6.(2022·四川宜宾·八年级期末)已知RtABC中,∠ACB=90°,AC=BC,AB=4,D为BC的中点,E是线段AB上一点,连接CE、DE,则CE+DE的最小值是( )
A.2 B.2 C.4 D.2+2
7.(2022·广东·深圳市福田区第二实验学校八年级期中)如图,在底面半径为2,(π取3)高为8的圆柱体上有只小虫子在A点,它想爬到B点,则爬行的最短路程是( )
A.10 B.8 C.5 D.4
8.(2021·浙江·宁波市第七中学八年级期中)如果△ABC的三个顶点A,B,C所对的边分别为a,b,c.那么下列条件中能判断△ABC是直角三角形的是( )
A.∠A:∠B:∠C=3:4:5 B.∠A=25°,∠B=75°
C.a=,b=,c= D.a=6,b=10,c=12
9.(2021·全国·八年级单元测试)如图,在平面直角坐标系xOy中,已知点P(m,m),过点P作OP的垂线交函数(k>1)的图象于点Q.若Q的横坐标为1,且OP2﹣PQ2=6,则k的值为( )
A.2 B.3 C. D.4
10.(2021·江西九江·八年级期末)如图,在△ABC中,AB=6,AC=8,BC=10,△ABD,△ACE,△BCF都是等边三角形,下列结论中:①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=135°;④S四边形AEFD=20.正确的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题:本题共8个小题,每题3分,共24分。
11.(2021·全国·八年级单元测试)已知△ABC中,AB=17,AC=10,BC边上的高AD=8.则边BC的长为_______.
12.(2021·全国·八年级单元测试)已知等腰三角形的腰长是13cm,底边长10cm,则该等腰三角形的面积是_______cm2.
13.(2021·河南·郑州枫杨外国语学校八年级期中)如图,在△ABC中,点D是BC的中点,若AB=5,AC=13,AD=6,则BC的长为 ______.
14.(2021·浙江·温州市南浦实验中学八年级期中)如图,点D在△ABC内,∠BDC=90°,AB=3,AC=BD=2,CD=1,则图中阴影部分的面积为 _______________.
15.(2022·重庆黔江·八年级期末)如图是放在地面上的一个长方体盒子,其中,,,点在棱上,且,点是的中点,一只蚂蚁要沿着长方体盒子的表面从点爬行到点,它需要爬行的最短路程为______.
16.(2022·重庆市育才中学八年级期末)如图所示,和都是等腰直角三角形,,平分,连接、,取的中点,连接,若,则与的面积之比为______.
17.(2021·上海市奉贤区古华中学九年级期中)如图,在4×3的正方形网格中,△ABC与△DEC的顶点都在边长为1的小正方形的顶点上,则∠BAC+∠CDE=___度.
18.(2022·江苏东台·九年级期末)如图,点P在第一象限,△ABP是边长为2的等边三角形,当点A在x轴的正半轴上运动时,点B随之在y轴的正半轴上运动,运动过程中,点P到原点的最大距离是______;若将△ABP的PA边长改为,另两边长度不变,则点P到原点的最大距离变为______.
三、解答题:本题共7个小题,19-23每题7分,24小题9分,25每题12分,共56分。
19.(2021·全国·八年级单元测试)如图,中,D为边上一点,且.
(1)求证:;
(2)若,,求的长.
20.(2021·全国·八年级单元测试)如图,红星村A和幸福村B在一条小河的同侧,它们到河岸的距离,分别为1和3,又知道的长为3,现要在河岸上建一水厂向两村输送自来水,铺设水管的工程费用为每千米20000元.
(1)请在上选择水厂位置,使铺设水管的费用最省(作图工具不限,保留作图痕迹);
(2)求铺设水管的最省总费用.
21.(2021·广东·珠海市文园中学八年级期中)如图,两个全等的等边三角形△ABC与△ACD,边长为6,高为a,在拼成的四边形ABCD中,点E、F分别为AB、AD边上的动点,满足BE=AF,连接EF,CE,CF.
(1)求证:△CEF是等边三角形;
(2)△AEF周长的最小值是 .(用含a的式子表示)
22.(2021·全国·八年级单元测试)如图,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条路CH,测得CB=1.5千米,CH=1.2千米,HB=0.9千米.
(1)问CH是否为从村庄C到河边的最近路?请通过计算加以说明;
(2)求新路CH比原路CA少多少千米?
23.(2021·全国·八年级单元测试)课间,小明拿着王老师的等腰直角三角板玩,三角板不小心掉到墙缝中.我们知道两堵墙都是与地面垂直的,如图.王老师没有批评他,但要求他完成如下两个问题:
(1)试说明;
(2)从三角板的刻度知AC=25cm,算算一块砖的厚度.(每块砖的厚度均相等)小明先将问题所给条件做了如下整理:如图,中,CA=CB,∠ACB=90°,AD⊥DE于D,BE⊥DE于E.请你帮他完成上述问题.
24.(2021·江苏·苏州工业园区星湾学校八年级期中)如图,在网格中,每个小正方形的边长都为1.
(1)的面积为________;
(2)判断的形状,并说明理由.
(3)求边上的高.
25.(2022·湖南广益实验中学八年级期末)我们规定,三角形任意两边的“广益值”等于第三边上的中线和这边一半的平方差.如图1,在中,是边上的中线,与的“广益值”就等于的值,可记为
(1)在中,若,,求的值.
(2)如图2,在中,,,求,的值.
(3)如图3,在中,是边上的中线,,,,求和的长.
第18章 勾股定理 单元综合能力测试
单选题:本题共10个小题,每小题2分,共20分。在每小题给出的四个选项中只有一项是符合题目要求的。
1.(2022·山东槐荫·八年级期末)直角三角形的两直角边长分别为5和12,则斜边长为( )
A.13 B.14 C. D.1
【答案】A
【分析】根据勾股定理,即可求得斜边长.
【详解】解:由题意得,该直角三角形的斜边长为:
故选:A.
【点睛】此题主要考查勾股定理,熟练掌握勾股定理即可解题.
2.(2022·全国·八年级期中)已知一个的两边长分别为3和4,则第三边长的平方是( )
A.25 B.14 C.7 D.7或25
【答案】D
【分析】由于4是三角形的直角边与斜边不能确定,故应分两种情况进行讨论.
【详解】解:由于4是三角形的直角边与斜边不能确定,故应分两种情况进行讨论:
(1)3、4都为直角边,由勾股定理得,斜边为5;
(2)3为直角边,4为斜边,由勾股定理得,直角边为.
∴第三边长的平方是25或7,
故选:D.
【点睛】本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.
3.(2021·江苏江阴·八年级期中)下列长度的三条线段能组成直角三角形的是( )
A.4,6,8 B.6,8,10 C.6,9,10 D.5,11,13
【答案】B
【分析】根据勾股定理的逆定理:两边的平方和等于第三边的平方,即可完成解答.
【详解】解:A、,故不能组成直角三角形;B、,故能组成直角三角形;C、,故不能组成直角三角形;D、,故不能组成直角三角形;
故选:B
【点睛】本题考查了勾股定理的逆定理,熟练掌握此定理是关键.
4.(2022·江苏江阴·八年级期末)已知,,分别是的三边,根据下列条件能判定为直角三角形的是( )
A.,, B.,,
C.,, D.,,
【答案】B
【分析】根据勾股定理的逆定理对四个选项进行逐一判断即可.
【详解】解:A、∵22+32≠42,∴不能构成直角三角形,故本选项错误;B、∵52+122=132,∴能构成直角三角形,故本选项正确;C、∵62+82≠122,∴能构成直角三角形,故本选项错误;D、∵62+122≠152,∴不能构成直角三角形,故本选项错误.
故选:B.
【点睛】本题考查的是勾股定理的逆定理,即如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.
5.(2022·全国·八年级期末)已知三角形的三边长分别为a,b,c,且a+b=10,ab=18,c=8,则该三角形的形状是( )
A.等腰三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形
【答案】B
【分析】根据完全平方公式利用a+b=10,ab=18求出,即可得到三角形的形状.
【详解】解:∵a+b=10,ab=18,
∴=(a+b)2-2ab=100-36=64,
∵,c=8,
∴=64,
∴=,
∴该三角形是直角三角形,
故选:B.
【点睛】此题考查勾股定理的逆定理,完全平方公式,能够利用完全平方公式由已知条件求出是解题的关键.
6.(2022·四川宜宾·八年级期末)已知RtABC中,∠ACB=90°,AC=BC,AB=4,D为BC的中点,E是线段AB上一点,连接CE、DE,则CE+DE的最小值是( )
A.2 B.2 C.4 D.2+2
【答案】B
【分析】作点C关于AB的对称点,连接,与AB交于点E,作DF于点F,则CE=,CE+DE= +DE,线段即为CE+DE得最小值.
【详解】解:如图,作点C关于AB的对称点,连接,与AB交于点E,作DF于点F,
则CE=,CE+DE= +DE,线段即为CE+DE得最小值.
∠ACB=90°,AC=BC,AB=4,
D为BC的中点,
CD=BD=BC=×4=2
CF=DF=,CC'=2CG=2×=
故选:B.
【点睛】此题考查了线路最短的问题,勾股定理,确定动点E何位置时,使DE+CE的值最小是解题的关键.
7.(2022·广东·深圳市福田区第二实验学校八年级期中)如图,在底面半径为2,(π取3)高为8的圆柱体上有只小虫子在A点,它想爬到B点,则爬行的最短路程是( )
A.10 B.8 C.5 D.4
【答案】A
【分析】若蚂蚁从侧表面从A爬行到B,首先将此圆柱展成平面图,根据两点间线段最短,可得AB最短,由勾股定理即可求得需要爬行的最短路程.
【详解】解:若蚂蚁从侧表面从A爬行到B,将此圆柱展成平面图得:
∵圆柱的高等于8,底面半径为2(π=3),
∴AC=8,BC==4π=6,
∴AB=10.
根据两点之间线段最短,蚂蚁从侧表面从A爬行到B最短路径为10.
故选:A.
【点睛】本题主要考查了平面展开图求最短路径问题,将圆柱体展开,根据两点之间线段最短,运用勾股定理解答是解题关键.
8.(2021·浙江·宁波市第七中学八年级期中)如果△ABC的三个顶点A,B,C所对的边分别为a,b,c.那么下列条件中能判断△ABC是直角三角形的是( )
A.∠A:∠B:∠C=3:4:5 B.∠A=25°,∠B=75°
C.a=,b=,c= D.a=6,b=10,c=12
【答案】C
【分析】根据三角形内角和定理得出,再根据求出最大角,再根据直角三角形的判定即可判断选项;根据三角形的内角和定理求出,即可判断选项;根据勾股定理的逆定理即可判断选项、选项.
【详解】解:.,,
最大角,
不是直角三角形,故本选项不符合题意;
.,,
,
不是直角三角形,故本选项不符合题意;
.,,,
,
是直角三角形,故本选项符合题意;
.,,,
,
不是直角三角形,故本选项不符合题意;
故选:C.
【点睛】本题考查了三角形内角和定理和勾股定理的逆定理,解题的关键是能熟记勾股定理的逆定理和三角形内角和等于180°.
9.(2021·全国·八年级单元测试)如图,在平面直角坐标系xOy中,已知点P(m,m),过点P作OP的垂线交函数(k>1)的图象于点Q.若Q的横坐标为1,且OP2﹣PQ2=6,则k的值为( )
A.2 B.3 C. D.4
【答案】B
【分析】根据点P(m,m)可得均为等腰直角三角形,根据OP2﹣PQ2=6得出,求出m值即可求得k的值.
【详解】解:作,,
P(m,m),
,
,
,
均为等腰直角三角形,
,
,
,
即,
解得:,
,
点的纵坐标为,
,
将点Q代入中,
得:,
故选:B.
【点睛】本题主要考查一次函数函数图像,等腰三角形以及勾股定理,根据已知条件求出m的值是解题的关键.
10.(2021·江西九江·八年级期末)如图,在△ABC中,AB=6,AC=8,BC=10,△ABD,△ACE,△BCF都是等边三角形,下列结论中:①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=135°;④S四边形AEFD=20.正确的个数是( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【分析】由,得出,故①正确;再由证得,得,同理,得,则四边形是平行四边形,故②正确;然后由平行四边形的性质得,则③错误;最后求出,故④错误;即可得出答案.
【详解】解:,,,,
,
是直角三角形,,
,故①正确;
,都是等边三角形,
,
,
和都是等边三角形,
,,,
,
在与中,
,
,
,
同理可证:,
,
四边形是平行四边形,故②正确;
,故③错误;
过作于,如图所示:
则,
四边形是平行四边形,
,
,
,故④错误;
正确的个数是2个,
故选:B.
【点睛】本题考查了平行四边形的判定与性质、勾股定理的逆定理、全等三角形的判定与性质、等边三角形的性质、含角的直角三角形的性质等知识;熟练掌握平行四边形的判定与性质,证明是解题的关键.
二、填空题:本题共8个小题,每题3分,共24分。
11.(2021·全国·八年级单元测试)已知△ABC中,AB=17,AC=10,BC边上的高AD=8.则边BC的长为_______.
【答案】21或9
【分析】根据题意,可能是锐角三角形或者钝角三角形,分两种情况进行讨论作图,然后利用勾股定理即可求解.
【详解】解:在中,,,BC边上高,
如图所示,当为锐角三角形时,
在中,,由勾股定理得:
,
∴,
在中,,由勾股定理得:
,
∴,
∴BC的长为:;
如图所示:当为钝角三角形时,
在中,,由勾股定理得:
,
∴,
在中,,由勾股定理得:
,
∴,
∴BC的长为:;
综上可得:BC的长为:21或9.
故答案为:21或9.
【点睛】题目主要考查勾股定理,进行分类讨论作出图象运用勾股定理解直角三角形是解题关键.
12.(2021·全国·八年级单元测试)已知等腰三角形的腰长是13cm,底边长10cm,则该等腰三角形的面积是_______cm2.
【答案】60
【分析】根据等腰三角形三线合一定理和勾股定理即可求得底边的高,从而求得三角形面积.
【详解】解:如图所示:AB=AC=13cm,BC=10cm
作AD⊥BC于D,则∠ADB=90°
∴,
∴,
∴△ABC的面积=,
故答案为:60.
【点睛】本题考查勾股定理和等腰三角形的性质,掌握等腰三角形三线合一是解题关键.
13.(2021·河南·郑州枫杨外国语学校八年级期中)如图,在△ABC中,点D是BC的中点,若AB=5,AC=13,AD=6,则BC的长为 ______.
【答案】
【分析】延长AD到E,使DE=AD,连接BE.先运用SAS证明△ADC≌△EDB,得出BE=13.再由勾股定理的逆定理证明出∠BAE=90°,然后在△ABD中运用勾股定理求出BD的长,从而得出BC=2BD.
【详解】解:延长AD到E,使DE=AD,连接BE.
在△ADC与△EDB中,
,
∴△ADC≌△EDB(SAS),
∴AC=BE=13.
在△ABE中,AB=5,AE=12,BE=13,
∴AB2+AE2=BE2,
∴∠BAE=90°.
在△ABD中,∠BAD=90°,AB=5,AD=6,
∴BD=,
∴BC=.
故答案为:.
【点睛】本题考查了全等三角形的判定与性质,勾股定理及其逆定理,综合性较强,难度中等.题中延长中线的一倍是常用的辅助线的作法.
14.(2021·浙江·温州市南浦实验中学八年级期中)如图,点D在△ABC内,∠BDC=90°,AB=3,AC=BD=2,CD=1,则图中阴影部分的面积为 _______________.
【答案】##
【分析】根据勾股定理和,,,可以先求出的长,然后根据勾股定理的逆定理可以判断的形状,从而可以求出阴影部分的面积.
【详解】解:,,,
,
,,
,
是直角三角形,,
阴影,
故答案为:.
【点睛】本题考查勾股定理的逆定理、勾股定理、三角形的面积,解题的关键是求出的长.
15.(2022·重庆黔江·八年级期末)如图是放在地面上的一个长方体盒子,其中,,,点在棱上,且,点是的中点,一只蚂蚁要沿着长方体盒子的表面从点爬行到点,它需要爬行的最短路程为______.
【答案】10
【分析】利用平面展开图有两种情况,画出图形利用勾股定理求出MN的长即可.
【详解】解:如图,
∵AB=9,BC=GF=6,BF=5,点是的中点,
∴BM=9-3=6,BN=5+3=8,
∴
如图2,
∵AB=8,BC=GF=6,BF=5,
∴PM=9-3+3=9,NP=5,
∴.
∵因为,所以蚂蚁沿长方体表面从点爬行到点的最短距离的10
故答案为:10
【点睛】此题主要考查了平面展开图的最短路径问题和勾股定理的应用,利用展开图有两种情况分析得出是解题关键.
16.(2022·重庆市育才中学八年级期末)如图所示,和都是等腰直角三角形,,平分,连接、,取的中点,连接,若,则与的面积之比为______.
【答案】4:5
【分析】延长AE交BC于点G,连接BE,过点F作交BA的延长线于点H,根据等腰直角三角形的性质及角平分线的计算可得,AG平分,利用等腰三角形“三线合一”性质得出且,设,则,由勾股定理及线段间的数量关系得出,,计算出的面积,结合图形及题意可得,根据等角对等边得出为等腰直角三角形,利用勾股定理可得,结合图形计算的面积,最后求面积比即可.
【详解】解:如图所示:延长AE交BC于点G,连接BE,过点F作交BA的延长线于点H,
∵与均为等腰直角三角形,
∴,,,
∵AC平分,
∴,
∴,
∴AG平分,
∴且,
∵,
∴,
设,则,
∴,
∵,,
∴,
∴,
∴,
∵,
∴,
∴,
∵D为CE中点,
∴,
∵与中,CD边和DE边上的高相等,都是点B到直线CE的距离,
∴,
∵,
∴,
∵,
∴,
∵,
∴,,
∴为等腰直角三角形,
∴,
∴,
∴,
∴,
故答案为:.
【点睛】题目主要考查角平分线计算,勾股定理,等腰三角形的判定和性质等,理解题意,结合图形,作出辅助线,综合运用这些知识点是解题关键.
17.(2021·上海市奉贤区古华中学九年级期中)如图,在4×3的正方形网格中,△ABC与△DEC的顶点都在边长为1的小正方形的顶点上,则∠BAC+∠CDE=___度.
【答案】
【分析】连接、,根据勾股定理以及勾股定理的逆定理求解即可.
【详解】解:连接、,如下图:
由勾股定理得,,,
,,
∵,,
∴,,
∴为等腰直角三角形,为直角三角形,
∴
∴
故答案为:
【点睛】此题考查了勾股定理以及勾股定理的逆定理,解题的关键是熟练掌握勾股定理以及勾股定理的逆定理.
18.(2022·江苏东台·九年级期末)如图,点P在第一象限,△ABP是边长为2的等边三角形,当点A在x轴的正半轴上运动时,点B随之在y轴的正半轴上运动,运动过程中,点P到原点的最大距离是______;若将△ABP的PA边长改为,另两边长度不变,则点P到原点的最大距离变为______.
【答案】 1+ 1+
【详解】解:根据当O到AB的距离最大时,OP的值最大,得到O到AB的最大值是AB=1,此时在斜边的中点M上,由勾股定理求出PM,即可求出答案;将△ABP的PA边长改为,另两边长度不变,根据,得到∠PBA=90°,由勾股定理求出PM即可.
详解:取AB的中点M,连OM,PM,
在Rt△ABO中,OM==1,在等边三角形ABP中,PM=,
无论△ABP如何运动,OM和PM的大小不变,当OM,PM在一直线上时,P距O最远,
∵O到AB的最大值是AB=1,此时在斜边的中点M上, 由勾股定理得:PM=,
∴OP=1+,
将△AOP的PA边长改为,另两边长度不变, ∵,
∴∠PBA=90°,由勾股定理得:PM=, ∴此时OP=OM+PM=1+.
点睛:本题主要考查对直角三角形斜边上的中线性质,坐标与图形性质,三角形的三边关系,勾股定理的逆定理等边三角形的性质等知识点的理解和掌握,能根据理解题意求出PD的值是解此题的关键.
三、解答题:本题共7个小题,19-23每题7分,24小题9分,25每题12分,共56分。
19.(2021·全国·八年级单元测试)如图,中,D为边上一点,且.
(1)求证:;
(2)若,,求的长.
【答案】(1)见详解;(2)8
【分析】
(1)根据∠ACB=90°,,推出∠B=∠DCB,得出CD=BD,再根据,得出CD=AD,从而得出AD=BD;
(2)根据(1)先求出AB的长,再根据勾股定理即可求出AC的长.
【详解】解:(1)∵∠ACB=90°,
∴∠A+∠B=90°,∠DCA+∠DCB=90°,
∵,
∴∠B=∠DCB,
∴CD=BD,
∵,
∴CD=AD,
∴AD=BD;
(2)由(1)得:AD=CD=BD,
∵CD=5,
∴AB=10,
∵BC=6,∠ACB=90°,
∴AC=.
【点睛】此题考查了勾股定理,等腰三角形的判定定理,根据在三角形中,等角等边对求出CD=AD=DB是解题的关键.
20.(2021·全国·八年级单元测试)如图,红星村A和幸福村B在一条小河的同侧,它们到河岸的距离,分别为1和3,又知道的长为3,现要在河岸上建一水厂向两村输送自来水,铺设水管的工程费用为每千米20000元.
(1)请在上选择水厂位置,使铺设水管的费用最省(作图工具不限,保留作图痕迹);
(2)求铺设水管的最省总费用.
【答案】(1)见解析;(2)100000元.
【分析】
(1)延长AC到F,使CF=AC,连接BF,交CD于E,则E为所求;
(2)过B作BN⊥CA,交CA的延长线于N,求出BN,NC长,根据勾股定理求出BF,即可得出答案.
【详解】解:(1)延长AC到F,使CF=AC,连接BF,交CD于E,
∵AC⊥CD,
∴AE=FE,
∴AE+BE=FE+BE=BF,
则在CD上选择水厂位置是E时,使铺设管道的费用最省;
(2)如上图,过B作BN⊥CA,交CA的延长线于N,
∴BN=CD=3km,CN=BD=3km,
∵AC=CF=1km,
∴NF=4km,
在Rt△BNF中,由勾股定理得:BF=km,
∵AC⊥CD,AC=CF,
∴AE=FE,
∴AE+BE=EF+BE=BF=5km,
∴铺设水管的最最省总费用是:20000×5=100000(元).
【点睛】本题考查了线段垂直平分线的性质及勾股定理,掌握线段垂直平分线的性质及勾股定理等知识是解题的关键,此类题目重点培养学生的动手操作能力和计算能力.
21.(2021·广东·珠海市文园中学八年级期中)如图,两个全等的等边三角形△ABC与△ACD,边长为6,高为a,在拼成的四边形ABCD中,点E、F分别为AB、AD边上的动点,满足BE=AF,连接EF,CE,CF.
(1)求证:△CEF是等边三角形;
(2)△AEF周长的最小值是 .(用含a的式子表示)
【答案】(1)证明见解析;(2)6+3
【分析】
(1)证明△BEC≌△AFC(SAS),可得结论;
(2)△AEF的周长=AE+AF+EF=AE+BE+EF=AB+EF=6+EF,推出EF的值最小时,△AEF的周长最小,因为△ECF是等边三角形,推出EF=CE,推出当CE⊥AB时,CE的值最小.
【详解】解:(1)证明:∵△ABC,△ACD是全等的等边三角形,
∴AC=BC,∠ABC=∠DAC=∠BCA=60°,
∵AF=BE,在△CBE和△CAF中,
,
∴△BEC≌△AFC(SAS),
∴CE=CF,∠BCE=∠ACF,
∴∠BCE+∠ACE=∠ACF+∠ACE,
∴∠ECF=∠BCA=60°,
∴△CEF是等边三角形.
(2)
解:∵△AEF的周长=AE+AF+EF=AE+BE+EF=AB+EF=6+EF,
∴EF的值最小时,△AEF的周长最小,
∵△ECF是等边三角形,
∴EF=CE,
∴当CE⊥AB时,CE的值最小,
∵△ABC是等边三角形,且CE⊥AB,
∴,
在Rt△AEC中,CE==3,
∴△AEF的周长的最小值为6+3,
故答案为:6+3.
【点睛】本题属于三角形综合题,考查了等边三角形的性质,全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考压轴题.
22.(2021·全国·八年级单元测试)如图,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条路CH,测得CB=1.5千米,CH=1.2千米,HB=0.9千米.
(1)问CH是否为从村庄C到河边的最近路?请通过计算加以说明;
(2)求新路CH比原路CA少多少千米?
【答案】解:(1)是,理由见详解; (2)新路CH比原路CA少0.05千米.
【分析】
(1)根据勾股定理的逆定理验证△CHB为直角三角形,进而得到CH⊥AB,再根据点到直线的距离垂线段最短即可解答;
(2)在△ACH中根据勾股定理解答即可.
【详解】解:(1)是,理由如下:
在△CHB中,
∵CH2+BH2=1.22+0.92=2.25=1.52=BC2,
即CH2+BH2=BC2,
∴△CHB为直角三角形,且∠CHB=90°,
∴CH⊥AB,
由点到直线的距离垂线段最短可知,CH是从村庄C到河边AB的最近路;
(2)设AC=x千米,
在Rt△ACH中,由已知设AC=x,AH=x-0.9,CH=1.2,
由勾股定理得:AC2=AH2+CH2
∴x2=(x-0.9)2+1.22,
解得x=1.25,即AC=1.25,
故AC-CH=1.25-1.2=0.05(千米)
答:新路CH比原路CA少0.05千米.
【点睛】本题考查勾股定理及勾股定理的逆定理的应用,熟练掌握勾股定理及逆定理是解决本题的关键.
23.(2021·全国·八年级单元测试)课间,小明拿着王老师的等腰直角三角板玩,三角板不小心掉到墙缝中.我们知道两堵墙都是与地面垂直的,如图.王老师没有批评他,但要求他完成如下两个问题:
(1)试说明;
(2)从三角板的刻度知AC=25cm,算算一块砖的厚度.(每块砖的厚度均相等)小明先将问题所给条件做了如下整理:如图,中,CA=CB,∠ACB=90°,AD⊥DE于D,BE⊥DE于E.请你帮他完成上述问题.
【答案】(1)证明见解析;(2)5cm
【分析】
(1)根据题意可得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,进而得到∠ADC=∠CEB=90°,再根据等角的余角相等可得∠BCE=∠DAC,再证明△ADC≌△CEB即可.
(2)利用(1)中全等三角形的性质进行解答.
【详解】解:证明:(1)如图:
∵AD⊥DE,BE⊥DE,
∴∠ADC=∠BEC=90°,
∴∠1+∠2=90°,
∵∠ACB=90°,
∴∠2+∠3=180°﹣90°=90°,
∵∠ADC=∠BEC=90°,
∴∠1=∠3,
由∠ADC=∠BEC=90°,∠1=∠3,CA=CB,
∴△ADC≌△CEB;
(2)设每块砖厚度为xcm,由①得,DC=BE=3xcm,AD=4xcm,
∵∠ADC=90°,
∴AD2+CD2=AC2,
即(4x)2+(3x)2=252,解得x=5,(x=﹣5舍去),
∴每块砖厚度为5cm.
【点睛】此题主要考查了全等三角形的应用,关键是正确找出证明三角形全等的条件.
24.(2021·江苏·苏州工业园区星湾学校八年级期中)如图,在网格中,每个小正方形的边长都为1.
(1)的面积为________;
(2)判断的形状,并说明理由.
(3)求边上的高.
【答案】(1)5;(2)△ABC是直角三角形,理由见解析;(3)2.
【分析】
(1)根据割补法即可求解;
(2)利用勾股定理的逆定理即可判断是直角三角形;
(3)过点C作CF⊥AB于点F,根据等积法即可求得CF值.
(1)
解:如图:
∵AE=1,BD=4,ED=4,EC=DC=2,
∴S△ABC=S梯形ABDE-S△BCD-S△ACE=
=
=
=10-4-1
=5,
故答案为:5;
(2)
解:△ABC是直角三角形,理由如下:
∵AB2=32+42=25,BC2=42+22=20,AC2=12+22=5,
∴BC2 +AC2=20+5=25,
即AB2= BC2 +AC2,
故△ABC是直角三角形.
(3)
解:如图:过点C作CF⊥AB于点F,
由(1)(2)知:S△ABC=5,AB=5,
∴S△ABC=,
即,
解得CF=2,
故边上的高为2.
【点睛】此题考查三角形面积,勾股定理及其逆定理,掌握基本知识是解答此题的关键.
25.(2022·湖南广益实验中学八年级期末)我们规定,三角形任意两边的“广益值”等于第三边上的中线和这边一半的平方差.如图1,在中,是边上的中线,与的“广益值”就等于的值,可记为
(1)在中,若,,求的值.
(2)如图2,在中,,,求,的值.
(3)如图3,在中,是边上的中线,,,,求和的长.
【答案】(1)AC=9;(2)ABAC=-72,BABC=216;(3)BC=2OC=2,AB=10.
【分析】
(1)在Rt中,根据勾股定理和新定义可得AO2-OC2=81=AC2;
(2)①先利用含30°的直角三角形的性质求出AO=2,OB=,再用新定义即可得出结论;
②先构造直角三角形求出BE,AE,再用勾股定理求出BD,最后用新定义即可得出结论;
(3)作BD⊥CD,构造直角三角形BCD,根据三角形面积关系求出BD,根据新定义和勾股定理逆定理得出三角形AOD是直角三角形,根据中线性质得出OA的长度,根据勾股定理求出OC,从而得出BC,再根据勾股定理求出CD,再求出AD,再运用勾股定理求出AB.
【详解】解:(1)已知如图:AO为BC上的中线,
在Rt中,
AO2-OC2=AC2
因为
所以AO2-OC2=81
所以AC2=81
所以AC=9.
(2)①如图2,取BC的中点D,连接AO,∵AB=AC,∴AO⊥BC,
在△ABC中,AB=AC,∠BAC=120°,∴∠ABC=30°,
在Rt△AOB中,AB=12,∠ABC=30°,∴AO=6,OB==,
∴ABAC=AO2﹣BO2=36﹣108=﹣72,
②取AC的中点D,连接BD,∴AD=CD=AC=6,过点B作BE⊥AC交CA的延长线于E,在Rt△ABE中,∠BAE=180°﹣∠BAC=60°,∴∠ABE=30°,
∵AB=12,∴AE=6,BE=,
∴DE=AD+AE=12,
在Rt△BED中,根据勾股定理得,BD=
∴BABC=BD2﹣CD2=216;
(3)作BD⊥CD,
因为,,
所以BD=2,
因为,是边上的中线,
所以AO2-OC2=-64,
所以OC2-AO2=64,
由因为AC2=82=64,
所以OC2-AO2= AC2
所以∠OAC=90°
所以OA=
所以OC=
所以BC=2OC=2,
在Rt△BCD中,
CD=
所以AD=CD-AC=16-8=8
所以AB=
【点睛】考核知识点:勾股定理逆定理,含30°直角三角形性质.借助辅助线构造直角三角形,运用勾股定理等直角三角形性质解决问题是关键
