2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册6.2.3组合6.2.4组合数课件(26张ppt)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册6.2.3组合6.2.4组合数课件(26张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 408.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 10:05:49 | ||
图片预览








文档简介
(共26张PPT)
6.2.3 组合 6.2.4 组合数
第二课时
1、组合定义:
一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.
从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号
表示.
2、组合数:
3、组合数公式:
复习引入
例2.(1)凸五边形有多少条对角线?
(2)凸n(n>3)边形有多少条对角线?
例1.(1)平面内有10个点,以其中每2个点为端点的线段共有多少条?
(2)平面内有10个点,以其中每2个点为端点的有向线段共有多少条?
例题讲评
例3:在100件产品中有98件合格品,2件次品.产品检验时,从100件产品中任意抽出3件.
(1)一共有多少种不同的抽法
(2)抽出的3件中恰好有1件是次品的抽法有多少种
(3)抽出的3件中至少有1件是次品的抽法有多少种
(4)抽出的3件中至多有一件是次品的抽法有多少种
说明:“至少”“至多”的问题,通常用分类法或间接法求解.
【思路点拨】 本题属于组合问题中的最基本的问题,可根据题意分别对不同问题中的“含”与“不含”作出正确的判断和分析.注意“至少”、“至多”问题,运用间接法解会简化思维过程.
例题讲评
“至少”“至多”的问题
(1)甲、乙、丙三人必须当选;
(2)甲、乙、丙三人不能当选;
(3)甲必须当选,乙、丙不能当选;
(4)甲、乙、丙三人只有一人当选;
(5)甲、乙、丙三人至多2人当选;
(6)甲、乙、丙三人至少1人当选;
在一次数学竞赛中,某学校有12人通过了初试,学校要从中选出5人去参加市级培训,在下列条件下,有多少种不同的选法?
练习巩固
例题讲评
例4、有翻译人员11名,其中5名仅通英语、4名仅通法语,还有2名英、法语皆通.现欲从中选出8名,其中4名译英语,另外4名译法语,一共可列多少张不同的名单?
多面手的合理分类与分步策略
例5 (1)平面内有9个点,其中4个点在一条直线上,此外没有3个点在一条直线上,过这9个点可确定多少条直线?可以作多少个三角形?
(2)空间12个点,其中5个点共面,此外无任何4个点共面,这12个点可确定多少个不同的平面?
例题讲评
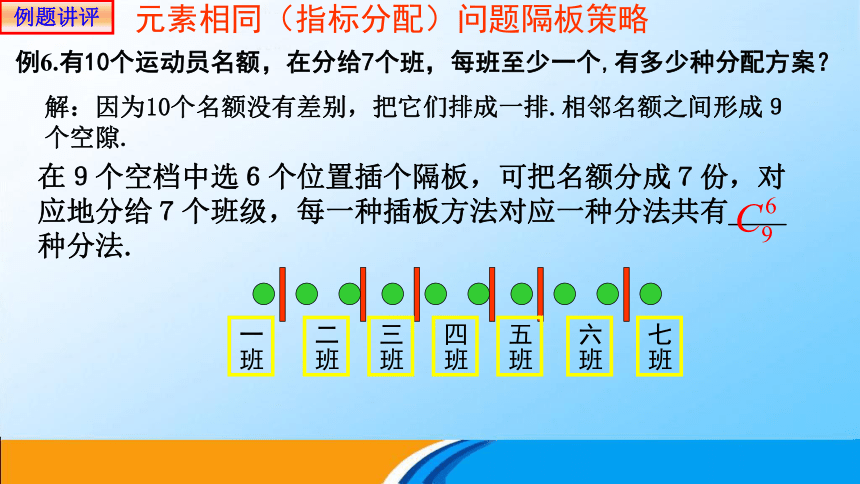
元素相同(指标分配)问题隔板策略
例6.有10个运动员名额,在分给7个班,每班至少一个,有多少种分配方案?
解:因为10个名额没有差别,把它们排成一排.相邻名额之间形成9个空隙.
在9个空档中选6个位置插个隔板,可把名额分成7份,对应地分给7个班级,每一种插板方法对应一种分法共有____种分法.
一班
二班
三班
四班
五班
六班
七班
例题讲评
练习1:某城新建的一条道路上有12只路灯,为了节省用电而不影响正常的照明,可以熄灭其中三盏灯,但两端的灯不能熄灭,也不能熄灭相邻的两盏灯,可以熄灭的方法共有( )
(A) 种(B) 种 (C) 种 (D) 种
A
练习2:从一楼到二楼的楼梯有17级,上楼时可以一步走一级,也可以一步走两级,若要求11步走完,则有多少种不同的走法?
例题讲评
构造模型策略
6.2.3 组合 6.2.4 组合数
第三课时
例1 四本不同的书平均分成两堆,问有多少种分法?
思考:这样分堆会有重复吗?
等分组与不等分组的分组分配问题
例题讲评
怎么样才能去掉重复的分堆呢?
三国、水浒
西游、红楼
三国、西游
水浒、红楼
三国、红楼
西游、水浒
三国、水浒
西游、红楼
三国、西游
水浒、红楼
三国、红楼
西游、水浒
例1变式 六本不同的书平均分成三堆,问有多少种分法?
等分组与不等分组的分组分配问题
例题讲评
a、b
c、d
e、f
a、b
e、f
c、d
c、d
a、b
e、f
c、d
e、f
a、b
e、f
a、b
c、d
e、f
c、d
a、b
每一种重复6次
例1变式 六本不同的书平均分成三堆,问有多少种分法?
等分组与不等分组的分组分配问题
例题讲评
每一种重复6次
例1 四本不同的书平均分成两堆,问有多少种分法?
每一种重复2次
完全均分问题
例1变式2 八本不同的书平均分成四堆,问有多少种分法?
例1变式3 九本不同的书平均分成三堆,问有多少种分法?
例2 四本不同的书平均分成1,1,2三堆,问有多少种分法?
等分组与不等分组的分组分配问题
例题讲评
三国
西游、红楼
水浒
三国
西游、红楼
水浒
水浒
西游、红楼
三国
三国
水浒、红楼
西游
显然,这两个分堆方法是同一个方案
显然,这两个分堆方法是不同方案
上述公式中分堆方法重复了两遍
例2变式 六本不同的书平均分成1,1,4三堆,问有多少种分法?
等分组与不等分组的分组分配问题
例题讲评
部分均分问题
例2变式2 八本不同的书平均分成1,2,2,3四堆,问有多少种分法?
例2变式3 六本不同的书平均分成1,1,2,2四堆,问有多少种分法?
例3 六本不同的书分成1,2,3三堆,问有多少种分法?
等分组与不等分组的分组分配问题
例题讲评
可根据树状图穷举,方案应为60种.
完全不均分问题
例4 六本不同的书
(1)平均分给三个同学,问有多少种分法?
不同元素的分组与分配问题
法1:边取边分,有 种分法.
法2:分析,可以考虑先分组, 再分配给三个同学,所以
有 分法.
不同元素的分组与分配问题
例4 六本不同的书
(2)如果按照4,1,1分给三个同学,问有多少种分法?
(3)如果按照3,2,1分给三个同学,问有多少种分法?
解:先分组,后分配
解:先分组,后分配
解:可以考虑,先分组,再分配.
分组可以按2,2,2分,4,1,1分,3,2,1分,所以有
(4)分给三个同学,每个同学至少有一本,问有多少种分法?
练习1
1. 当前新冠肺炎疫情形势依然严峻,防控新冠肺炎疫情需常态化为加大宣传力度,提高防控能力,某区疾控中心拟安排某4名医务人员到流动人口较多的某3个乡镇进行疫情防控督查,每个医务人员只去一个乡镇,每个乡镇至少安排一名医务人员,则不同的安排方法共有___种.
2.将5位同学分配到三个班,每班至少一人,共有多少种不同的分配方法?
36
150
不同元素的分组与分配问题
(1)完全平均分组:在分组时,每组元素的个数都相等.
①只分组无分配时,需要除以这几组的“全排列”,以确保消去重复;
②分组且分配时,一种方法是先分组再分配;另一种方法是可以用分步乘法
计数原理解题.
(2)部分平均分组:在分组时,每组的个数是不均等的,而是有一部分个数相同.
需要除以相同的组的“全排列”,保证没有重复.
(3)非平均分组:每组所要分的元素个数是不相同的.这种分组不考虑重复现象.
解题思想:先分组、后分配
混合问题,先“组”后“排”
例5 对某种产品的6件不同的正品和4件不同的次品,一一进行测试,至区分出所有次品为止,若所有次品恰好在第5次测试时全部发现,则这样的测试方法有种可能?
解:由题意知前5次测试恰有4次测到次品,且第5次测试是次品.故有: 种可能.
例题讲评
练习:1、某学习小组有5个男生3个女生,从中选3名男生和1名女生参加三项竞赛活动,每项活动至少有1人参加,则有不同参赛方法______种.
解:采用先分组后排方法:
2、3 名医生和 6 名护士被分配到 3 所学校为学生体检,每校分配 1 名医生和 2 名护士,不同的分配方法共有多少种
解法一:先组队后分校(先分堆后分配)
解法二:依次确定到第一、第二、第三所学校去的医生和护士.
巩固练习
例5、8双互不相同的鞋子混装在一只口袋中,从中任意取出4只,试求满足如下条件各有多少种情况:
(1)4只鞋子恰有两双;
(2) 4只鞋子没有成双的;
(3) 4只鞋子只有一双.
【点评】 本题解决的办法是将“事件”进行等价处理,如第一问“4只鞋子没有成双的”相当于这四只鞋子来自于4双.因此分两步完成,第一步取四双鞋,第二步从每双鞋中各取一只.希同学们好好的体会这种思想方法
例题讲评
2、从6位同学中选出4位参加一个座谈会,要求张、王两人中至多有一个人参加,则有不同的选法种数为 .
3、要从8名男医生和7名女医生中选5人组成一个医疗队,如果其中至少有2名男医生和至少有2名女医生,则不同的选法种数为( )
1、把6个学生分到一个工厂的三个车间实习,每个车间2人,若甲必须分到一车间,乙和丙不能分到二车间,则不同的分法有 种 .
9
9
C
巩固练习
5、在如图7×4的方格纸上(每小方格均为正方形)
(1)其中有多少个矩形?
(2)其中有多少个正方形?
巩固练习
4、从7人中选出3人分别担任学习委员、宣传委员、体育委员,则甲、乙两人不都入选的不同选法种数共有( )
D
3、从6人中选人分别到巴黎、伦敦、悉尼、莫斯科四个城市游览,要求每个城市有一人游览,每人只游览一个城市,且这6人中甲乙不去巴黎游览,则不同的选择方案共有( )种
A.300 B.240 C.144 D.96
4、四棱锥的8条棱分别代表8种不同的化工产品,有公共点的两条棱所代表的化工产品放在同一仓库是危险的,没有公共点的两条棱所代表的化工产品放在同一仓库是安全的.现打算用编号为(1)、(2)、(3)、(4)的四个仓库存放这8种化工产品,那么安全存放的不同方法种数为( )
A.96 B.48 C.24 D.0
B
B
巩固练习
6.2.3 组合 6.2.4 组合数
第二课时
1、组合定义:
一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.
从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号
表示.
2、组合数:
3、组合数公式:
复习引入
例2.(1)凸五边形有多少条对角线?
(2)凸n(n>3)边形有多少条对角线?
例1.(1)平面内有10个点,以其中每2个点为端点的线段共有多少条?
(2)平面内有10个点,以其中每2个点为端点的有向线段共有多少条?
例题讲评
例3:在100件产品中有98件合格品,2件次品.产品检验时,从100件产品中任意抽出3件.
(1)一共有多少种不同的抽法
(2)抽出的3件中恰好有1件是次品的抽法有多少种
(3)抽出的3件中至少有1件是次品的抽法有多少种
(4)抽出的3件中至多有一件是次品的抽法有多少种
说明:“至少”“至多”的问题,通常用分类法或间接法求解.
【思路点拨】 本题属于组合问题中的最基本的问题,可根据题意分别对不同问题中的“含”与“不含”作出正确的判断和分析.注意“至少”、“至多”问题,运用间接法解会简化思维过程.
例题讲评
“至少”“至多”的问题
(1)甲、乙、丙三人必须当选;
(2)甲、乙、丙三人不能当选;
(3)甲必须当选,乙、丙不能当选;
(4)甲、乙、丙三人只有一人当选;
(5)甲、乙、丙三人至多2人当选;
(6)甲、乙、丙三人至少1人当选;
在一次数学竞赛中,某学校有12人通过了初试,学校要从中选出5人去参加市级培训,在下列条件下,有多少种不同的选法?
练习巩固
例题讲评
例4、有翻译人员11名,其中5名仅通英语、4名仅通法语,还有2名英、法语皆通.现欲从中选出8名,其中4名译英语,另外4名译法语,一共可列多少张不同的名单?
多面手的合理分类与分步策略
例5 (1)平面内有9个点,其中4个点在一条直线上,此外没有3个点在一条直线上,过这9个点可确定多少条直线?可以作多少个三角形?
(2)空间12个点,其中5个点共面,此外无任何4个点共面,这12个点可确定多少个不同的平面?
例题讲评
元素相同(指标分配)问题隔板策略
例6.有10个运动员名额,在分给7个班,每班至少一个,有多少种分配方案?
解:因为10个名额没有差别,把它们排成一排.相邻名额之间形成9个空隙.
在9个空档中选6个位置插个隔板,可把名额分成7份,对应地分给7个班级,每一种插板方法对应一种分法共有____种分法.
一班
二班
三班
四班
五班
六班
七班
例题讲评
练习1:某城新建的一条道路上有12只路灯,为了节省用电而不影响正常的照明,可以熄灭其中三盏灯,但两端的灯不能熄灭,也不能熄灭相邻的两盏灯,可以熄灭的方法共有( )
(A) 种(B) 种 (C) 种 (D) 种
A
练习2:从一楼到二楼的楼梯有17级,上楼时可以一步走一级,也可以一步走两级,若要求11步走完,则有多少种不同的走法?
例题讲评
构造模型策略
6.2.3 组合 6.2.4 组合数
第三课时
例1 四本不同的书平均分成两堆,问有多少种分法?
思考:这样分堆会有重复吗?
等分组与不等分组的分组分配问题
例题讲评
怎么样才能去掉重复的分堆呢?
三国、水浒
西游、红楼
三国、西游
水浒、红楼
三国、红楼
西游、水浒
三国、水浒
西游、红楼
三国、西游
水浒、红楼
三国、红楼
西游、水浒
例1变式 六本不同的书平均分成三堆,问有多少种分法?
等分组与不等分组的分组分配问题
例题讲评
a、b
c、d
e、f
a、b
e、f
c、d
c、d
a、b
e、f
c、d
e、f
a、b
e、f
a、b
c、d
e、f
c、d
a、b
每一种重复6次
例1变式 六本不同的书平均分成三堆,问有多少种分法?
等分组与不等分组的分组分配问题
例题讲评
每一种重复6次
例1 四本不同的书平均分成两堆,问有多少种分法?
每一种重复2次
完全均分问题
例1变式2 八本不同的书平均分成四堆,问有多少种分法?
例1变式3 九本不同的书平均分成三堆,问有多少种分法?
例2 四本不同的书平均分成1,1,2三堆,问有多少种分法?
等分组与不等分组的分组分配问题
例题讲评
三国
西游、红楼
水浒
三国
西游、红楼
水浒
水浒
西游、红楼
三国
三国
水浒、红楼
西游
显然,这两个分堆方法是同一个方案
显然,这两个分堆方法是不同方案
上述公式中分堆方法重复了两遍
例2变式 六本不同的书平均分成1,1,4三堆,问有多少种分法?
等分组与不等分组的分组分配问题
例题讲评
部分均分问题
例2变式2 八本不同的书平均分成1,2,2,3四堆,问有多少种分法?
例2变式3 六本不同的书平均分成1,1,2,2四堆,问有多少种分法?
例3 六本不同的书分成1,2,3三堆,问有多少种分法?
等分组与不等分组的分组分配问题
例题讲评
可根据树状图穷举,方案应为60种.
完全不均分问题
例4 六本不同的书
(1)平均分给三个同学,问有多少种分法?
不同元素的分组与分配问题
法1:边取边分,有 种分法.
法2:分析,可以考虑先分组, 再分配给三个同学,所以
有 分法.
不同元素的分组与分配问题
例4 六本不同的书
(2)如果按照4,1,1分给三个同学,问有多少种分法?
(3)如果按照3,2,1分给三个同学,问有多少种分法?
解:先分组,后分配
解:先分组,后分配
解:可以考虑,先分组,再分配.
分组可以按2,2,2分,4,1,1分,3,2,1分,所以有
(4)分给三个同学,每个同学至少有一本,问有多少种分法?
练习1
1. 当前新冠肺炎疫情形势依然严峻,防控新冠肺炎疫情需常态化为加大宣传力度,提高防控能力,某区疾控中心拟安排某4名医务人员到流动人口较多的某3个乡镇进行疫情防控督查,每个医务人员只去一个乡镇,每个乡镇至少安排一名医务人员,则不同的安排方法共有___种.
2.将5位同学分配到三个班,每班至少一人,共有多少种不同的分配方法?
36
150
不同元素的分组与分配问题
(1)完全平均分组:在分组时,每组元素的个数都相等.
①只分组无分配时,需要除以这几组的“全排列”,以确保消去重复;
②分组且分配时,一种方法是先分组再分配;另一种方法是可以用分步乘法
计数原理解题.
(2)部分平均分组:在分组时,每组的个数是不均等的,而是有一部分个数相同.
需要除以相同的组的“全排列”,保证没有重复.
(3)非平均分组:每组所要分的元素个数是不相同的.这种分组不考虑重复现象.
解题思想:先分组、后分配
混合问题,先“组”后“排”
例5 对某种产品的6件不同的正品和4件不同的次品,一一进行测试,至区分出所有次品为止,若所有次品恰好在第5次测试时全部发现,则这样的测试方法有种可能?
解:由题意知前5次测试恰有4次测到次品,且第5次测试是次品.故有: 种可能.
例题讲评
练习:1、某学习小组有5个男生3个女生,从中选3名男生和1名女生参加三项竞赛活动,每项活动至少有1人参加,则有不同参赛方法______种.
解:采用先分组后排方法:
2、3 名医生和 6 名护士被分配到 3 所学校为学生体检,每校分配 1 名医生和 2 名护士,不同的分配方法共有多少种
解法一:先组队后分校(先分堆后分配)
解法二:依次确定到第一、第二、第三所学校去的医生和护士.
巩固练习
例5、8双互不相同的鞋子混装在一只口袋中,从中任意取出4只,试求满足如下条件各有多少种情况:
(1)4只鞋子恰有两双;
(2) 4只鞋子没有成双的;
(3) 4只鞋子只有一双.
【点评】 本题解决的办法是将“事件”进行等价处理,如第一问“4只鞋子没有成双的”相当于这四只鞋子来自于4双.因此分两步完成,第一步取四双鞋,第二步从每双鞋中各取一只.希同学们好好的体会这种思想方法
例题讲评
2、从6位同学中选出4位参加一个座谈会,要求张、王两人中至多有一个人参加,则有不同的选法种数为 .
3、要从8名男医生和7名女医生中选5人组成一个医疗队,如果其中至少有2名男医生和至少有2名女医生,则不同的选法种数为( )
1、把6个学生分到一个工厂的三个车间实习,每个车间2人,若甲必须分到一车间,乙和丙不能分到二车间,则不同的分法有 种 .
9
9
C
巩固练习
5、在如图7×4的方格纸上(每小方格均为正方形)
(1)其中有多少个矩形?
(2)其中有多少个正方形?
巩固练习
4、从7人中选出3人分别担任学习委员、宣传委员、体育委员,则甲、乙两人不都入选的不同选法种数共有( )
D
3、从6人中选人分别到巴黎、伦敦、悉尼、莫斯科四个城市游览,要求每个城市有一人游览,每人只游览一个城市,且这6人中甲乙不去巴黎游览,则不同的选择方案共有( )种
A.300 B.240 C.144 D.96
4、四棱锥的8条棱分别代表8种不同的化工产品,有公共点的两条棱所代表的化工产品放在同一仓库是危险的,没有公共点的两条棱所代表的化工产品放在同一仓库是安全的.现打算用编号为(1)、(2)、(3)、(4)的四个仓库存放这8种化工产品,那么安全存放的不同方法种数为( )
A.96 B.48 C.24 D.0
B
B
巩固练习
