2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册8.3列联表与独立性检验课件(32张ppt)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册8.3列联表与独立性检验课件(32张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 10:07:08 | ||
图片预览










文档简介
8.3.1 分类变量与列联表
8.3列联表与独立性检验
一、提出问题
你认为吸烟与患肺癌有关系吗?
怎样用数学知识说明呢?
独立性检验方法
在现实生活中,人们经常需要回答一定范围内的两种现象或性质之间是否存在关联性或互相影响的问题。
例如:就读不同学校是否对学生的成绩有影响,不同班级学生用于体育锻炼的时间是都存在区别,吸烟是否会增加患肺癌的风险等。
分类变量:一种特殊的随机变量,以区别不同的现象或性质
分类变量的取值可以用实数表示,这些数值只作为编号使用,并没有通常的大小和运算意义
举例:
学生所在的班级可以用1,2,3等表示,
男性、女性可以用1,0表示
本节我们主要讨论取值于{0,1}的分类变量的关联性问题.
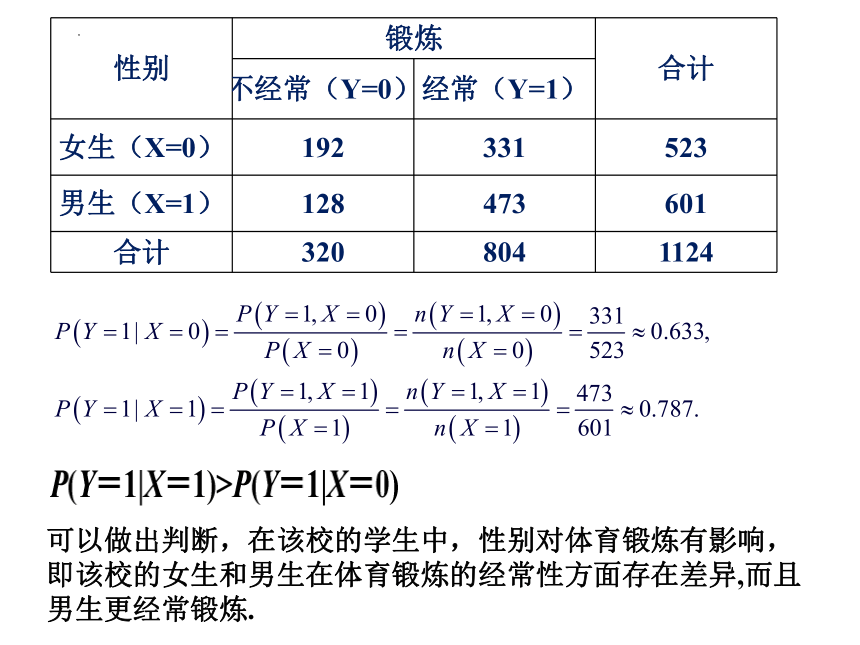
问题1:为了有针对性地提高学生体育锻炼的积极性,某中学需要了解性别因素是否对本校学生体育锻炼的经常性有影响,为此对学生是否经常锻炼的情况进行了普查.全校生的普查数据如下:523名女生中有331名经常锻炼;601名男生中有473名经常锻。你能利用这些数据,说明该校女生和男生在体育锻炼的经常性方面是否存在差异吗?
比较经常锻炼的学生在女生和男中的比率.
男生经常锻炼的比率比女生高出15.4个百分点,所以该校的女生和男生在体育锻炼的经常性方面有差异,而且男生更经常锻炼。
解法一:
问题1:为了有针对性地提高学生体育锻炼的积极性,某中学需要了解性别因素是否对本校学生体育锻炼的经常性有影响,为此对学生是否经常锻炼的情况进行了普查.全校生的普查数据如下:523名女生中有331名经常锻炼;601名男生中有473名经常锻。你能利用这些数据,说明该校女生和男生在体育锻炼的经常性方面是否存在差异吗?
解法二:
对于Ω中的每一名学生,分别令
性别对体育锻炼的经常性没有影响:
性别对体育锻炼的经常性有影响:
{5940675A-B579-460E-94D1-54222C63F5DA}性别
锻炼
合计
不经常(Y=0)
经常(Y=1)
女生(X=0)
192
331
523
男生(X=1)
128
473
601
合计
320
804
1124
可以做出判断,在该校的学生中,性别对体育锻炼有影响,即该校的女生和男生在体育锻炼的经常性方面存在差异,而且男生更经常锻炼.
二、2×2列联表的概念
{5940675A-B579-460E-94D1-54222C63F5DA}X
Y
合计
Y=0
Y=1
X=0
a
b
a+b
X=1
c
d
c+d
合计
a+c
b+d
n=a+b+c+d
分类变量X和Y的抽样数据的2?2列联表:
用途:可以清晰的给出成对分类变量数据的交叉分类频数。
在上面问题的两种解答中,使用了学校全部学生的调查数据,利用这些数据能够完全确定解答问题所需的比率和条件概率.
然而,对于大多数实际问题,我们无法获得所关心的全部对象的数据,因此无法准确计算出有关的比率或条件概率.
利用随机抽样获得一定数量的样本数据,再利用随机事件发生的频率稳定于概率的原理对问题答案作出推断。
反思
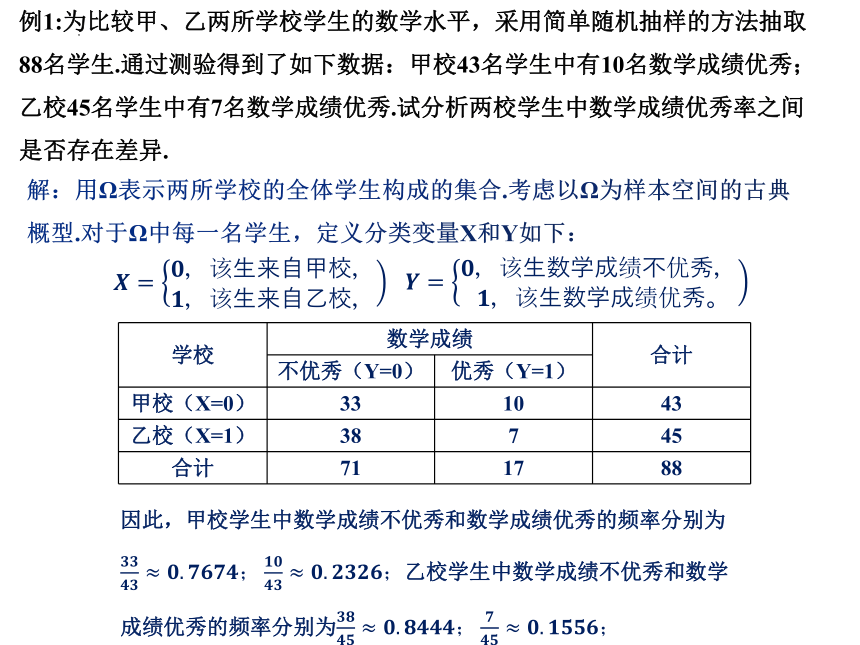
例1:为比较甲、乙两所学校学生的数学水平,采用简单随机抽样的方法抽取88名学生.通过测验得到了如下数据:甲校43名学生中有10名数学成绩优秀;乙校45名学生中有7名数学成绩优秀.试分析两校学生中数学成绩优秀率之间是否存在差异.
解:用Ω表示两所学校的全体学生构成的集合.考虑以Ω为样本空间的古典概型.对于Ω中每一名学生,定义分类变量X和Y如下:
????=????,该生来自甲校,????,该生来自乙校,
?
????=????,该生数学成绩不优秀,????,该生数学成绩优秀。
?
{5940675A-B579-460E-94D1-54222C63F5DA}学校
数学成绩
合计
不优秀(Y=0)
优秀(Y=1)
甲校(X=0)
33
10
43
乙校(X=1)
38
7
45
合计
71
17
88
因此,甲校学生中数学成绩不优秀和数学成绩优秀的频率分别为????????????????≈????.????????????????;????????????????≈????.????????????????;乙校学生中数学成绩不优秀和数学成绩优秀的频率分别为????????????????≈????.????????????????;????????????≈????.????????????????;
?
解:
我们可以用等高堆积条形图直观地展示上述计算结果:
甲校 乙校
通过比较发现,两个学校学生抽样数据中数学成绩优秀的频率存在差异,甲校的频率明显高于乙校的频率.依据频率稳定于概率的原理,我们可以推断那么甲校学生数学成绩优秀的概率大于乙校学生数学成绩优秀的概率。因此,可以认为两校学生的数学成绩优秀率存在差异,甲校学生的数学成绩优秀率比乙校学生的高。
例1:为比较甲、乙两所学校学生的数学水平,采用简单随机抽样的方法抽取88名学生.通过测验得到了如下数据:甲校43名学生中有10名数学成绩优秀;乙校45名学生中有7名数学成绩优秀.试分析两校学生中数学成绩优秀率之间是否存在差异.
因此,甲校学生中数学成绩不优秀和数学成绩优秀的频率分别为????????????????≈????.????????????????;????????????????≈????.????????????????;乙校学生中数学成绩不优秀和数学成绩优秀的频率分别为????????????????≈????.????????????????;????????????≈????.????????????????;
?
(1)频率分析法:通过对样本的每个分类变量的不同类别事件发生的频率大小进行比较来分析分类变量之间是否有关联关系.
如可以通过列联表中????????+????与????????+????值的大小粗略地判断分类变量x和Y之间有无关系.一般其值相差越大,分类变量有关系的可能性越大。
(2)图形分析法:与表格相比,图形更能直观地反映出两个分类变量间是否互相影响,常用等高堆积条形图展示列联表数据的频率特征.将列联表中的数据用高度相同的两个条形图表示出来,其中两列的数据分别对应不同的颜色,这就是等高堆积条形图.
等高堆积条形图可以展示列联表数据的频率特征,能够直观地反映出两个分类变量间是否相互影响。
?
三、两个分类变量之间关联关系的定性分析的方法
问题2:你认为“两校学生的数学成绩优秀率存在差异”这一结论是否有可能是错误的?
答:有可能。
“两校学生的数学成绩优秀率存在差异”这个结论是根据两个频率间存在差异推断出来的.有可能出现这种情况:在随机抽取的这个样本中,两个频率间确实存在差异,但两校学生的数学成绩优秀率实际上是没有差别的.对于随机样本而言,因为频率具有随机性,频率与概率之间存在误差,所以我们的推断可能犯错误,而且在样本容量较小时,犯错误的可能性会较大.因此,需要找到一种更为合理的推断方法,同时也希望能对出现错误推断的概率有一定的控制或估算.
独立性检验方法
练习
1. 在对人们饮食习惯的一次调查中,从某一居民小区中共调查了124位居民,其中六十岁及六十岁以上的70人,六十岁以下的54人.六十岁及六十岁以上的人中有43人的饮食以蔬菜为主,另外27人以肉类为主;六十岁以下的人中有21人的饮食以蔬菜为主,另外33人以肉类为主.请根据以上数据作出饮食习惯与年龄的列联表,并利用P(Y=1|X=0)与P(Y=1|X=1)判断二者是否有关系.
解:用Ω表示调查的124人所构成的集合,对于Ω中的每1位居民,定义一对分类变量X和Y:令X=0,以蔬菜为主,1,以肉类为主,Y=0,六十岁及六十岁以上,1,六十岁以下.
?
用表格整理数据,得到2×2列联表如下:
P(Y=1|X=0)=????(????=0,????=1)????(????=0)=2164≈0.328,
P(Y=1|X=1)=????(????=1,????=1)????(????=1)=3360=0.55.
显然二者具有较为明显的差距,据此可以
在某种程度上认为饮食习惯与年龄有关系.
?
饮食习惯
年龄
合计
六十岁及六十岁以上(Y=0)
六十岁以下(Y=1)
以蔬菜为主(X=0)
43
21
64
以肉类为主(X=1)
27
33
60
合计
70
54
124
2.假设有两个分类变量X与Y,它们的可能取值分别
为X=0,1和Y=0,1,其2×2列联表如下:
若X与Y之间没有影响,则m的值约为 ( )
A.8 B.9 C.14 D.19
?
X
Y
合计
Y=0
Y=1
X=0
10
18
28
X=1
m
26
m+26
合计
10+m
44
m+54
C
练习
3.为了解铅中毒病人与尿棕色素为阳性是否有关系,分别对病人组和对照组的尿液进行尿棕色素定性检查,结果如下:
试画出等高堆积条形图,分析铅中毒病人
与尿棕色素为阳性是否有关系.
分组
尿液定性
合计
阳性(Y=0)
阴性(Y=1)
病人组(X=0)
29
7
36
对照组(X=1)
9
28
37
合计
38
35
73
练习
解:病人组中尿棕色素为阳性和阴性的
频率分别为2936≈0.805 6和736≈0.194 4.
对照组中尿棕色素为阳性和阴性的频率分别为937≈0.243 2和2837≈0.756 8.
等高堆积条形图如图所示.其中两个深色条的高分别
代表铅中毒病人和对照组样本中尿棕色素为阳性的
频率.由图可以直观地看出铅中毒病人与对照组相比,
尿棕色素为阳性的频率差异明显,因此铅中毒病人与
尿棕色素为阳性有关系.
?
8.3.2 独立性检验
8.3列联表与独立性检验
提出零假设(原假设)H0:分类变量X和Y独立.
假定我们通过简单随机抽样得到了X和Y的抽样数据列联表,在列联表中,如果零假设H0成立,则应满足????????+????≈????????+????,即ad-bc≈0.因此,|?????????????????|越小,说明两个分类变量之间关系越弱;|?????????????????|越大,说明两个分类变量之间关系越强.
为了使不同样本容量的数据有统一的评判标准,基于上述分析,我们构造一个随机变量
?
用????????取值的大小作为判断零假设H0是否成立的依据,当它比较大时推断H0不成立,否则认为H0成立。这种利用????????的取值推断分类变量X和Y是否独立的方法称为????????独立性检验,读作“卡方独立性检验”,简称独立性检验.
?
????????=????(?????????????????)????(????+????)(????+????)(????+????)(????+????)
?
四、独立性检验公式及定义
对于任何小概率值????,可以找到相应的正实数????????,使得P(x≥????????)=????成立,我们称????????为????的临界值,这个临界值可作为判断????????大小的标准,概率值????越小,临界值????????越大.
?
{5940675A-B579-460E-94D1-54222C63F5DA}
0.1
0.05
0.01
0.005
0.001
2.706
3.841
6.635
7.879
10.828
基于小概率值????的检验规则:
?
当????????≥????????时,我们就推断H0不成立,即认为X和Y不独立,该推断犯错误的概率不超过????;
当?????????
????????独立性检验中几个常用的小概率值和相应的临界值
?
五、临界值的定义
例2:依据小概率值????=0.1的????????独立性检验,分析例1中的抽样数据,能否据此推
断两校学生的数学成绩优秀率有差异?
?
例1:为比较甲、乙两所学校学生的数学水平,采用简单随机抽样的方法抽取88名学生.通过测验得到了如下数据:甲校43名学生中有10名数学成绩优秀;乙校45名学生中有7名数学成绩优秀.试分析两校学生中数学成绩优秀率之间是否存在差异.
解:零假设为H0:分类变量X与Y相互独立,即两校学生的数学成绩优秀率无差异.
{5940675A-B579-460E-94D1-54222C63F5DA}学校
数学成绩
合计
不优秀(Y=0)
优秀(Y=1)
甲校(X=0)
33
10
43
乙校(X=1)
38
7
45
合计
71
17
88
所以
????????=????????(????????×?????????????×????????)????????????×????????×????????×????????≈????.?????????????
根据小概率值????=0.1的????????独立性检验,没有充分证据推断H0不成立,因此可以认为H0成立,即认为两校的数学成绩优秀率没有差异。
?
思考:例1和例2都是基于同一组数据的分析,但却得出了不同的结论,你能说明其中的原因吗?
例1只是根据一个样本的两个频率间存在差异得出两校学生数学成绩优秀率有差异的结论,并没有考虑由样本随机性可能导致的错误,所以那里的推断依据不太充分。
在例2中,我们用????????独立性检验对零假设H0进行了检验,通过计算,发现????????≈0.837小于α=0.1所对应的临界值2.706,因此认为没有充分证据推断H0不成立,所以接受H0,推断出两校学生的数学优秀率没有显著差异的结论,
这个检验结果意味着,抽样数据中两个频率的差异很有可能是由样本随机性导致的,因此,只根据频率的差异得出两校学生的数学成绩优秀率有差异的结论是不可靠的。
由此可见,相对于简单比较两个频率的推断,用????????独立性检验得到的结果更理性、更全面,理论依据也更充分。
?
当我们接受零假设H0时,也可能犯错误。我们不知道犯这类错误的概率p的大小,但是知道,若α越大,则p越小
例3:某儿童医院用甲、乙两种疗法治疗小儿消化不良.采用有放回简单随机抽样的方法对治疗情况进行检查,得到了如下数据:抽到接受甲种疗法的患儿67名,其中未治愈15名,治愈52名;抽到接受乙种疗法的患儿69名,其中未治愈6名,治愈63名.试根据小概率值????=0.005的独立性检验,分析乙种疗法的效果是否比甲种疗法好.
?
解:零假设为H0:疗法与疗效独立,即两种疗法效果没有差异.
将所给数据进行整理,得到两种疗法治疗数据的列联表,
{5940675A-B579-460E-94D1-54222C63F5DA}疗法
疗效
合计
未治愈
治愈
甲
15
52
67
乙
6
63
69
合计
21
115
136
根据列联表中的数据,经计算得到????????=????????????×(????????×?????????????????×????)????????????×????????×????????×????????????≈????.?????????????
根据小概率值????=0.005的????????独立性检验,没有充分证据推断 H0不成立,因此可以认为 H0成立,即认为两种疗法效果没有差异.
?
追问1:若对调两种疗法的位置或对调两种疗效的位置,这样做会影响????????取值的计算结果吗?
?
不影响
{5940675A-B579-460E-94D1-54222C63F5DA}疗法
疗效
合计
未治愈
治愈
甲
15
52
67
乙
6
63
69
合计
21
115
136
{5940675A-B579-460E-94D1-54222C63F5DA}疗法
疗效
合计
未治愈
治愈
乙
6
63
69
甲
15
52
67
合计
21
115
136
{5940675A-B579-460E-94D1-54222C63F5DA}疗法
疗效
合计
治愈
未治愈
甲
52
15
67
乙
63
6
69
合计
115
21
136
????????=????????????×(????????×?????????????????×????)????????????×????????×????????×????????????≈????.????????????
?
????????=????????????×(????????×?????????????×????????)????????????×????????×????????×????????????≈????.????????????
?
????????=????????????×(????????×?????????????×????????)????????????×????????×????????×????????????≈????.????????????
?
追问2:根据小概率值????=0.05的独立性检验,分析乙种疗法的效果是否比甲种疗法好.
?
解:零假设为H0:疗法与疗效独立,即两种疗法效果没有差异.
将所给数据进行整理,得到两种疗法治疗数据的列联表,
{5940675A-B579-460E-94D1-54222C63F5DA}疗法
疗效
合计
未治愈
治愈
甲
15
52
67
乙
6
63
69
合计
21
115
136
根据列联表中的数据,经计算得到????????=????????????×(????????×?????????????????×????)????????????×????????×????????×????????????≈????.????????????>????.????????????=????????.????????.
?
根据小概率值????=0.05的????????独立性检验,我们推断 H0不成立,即可以认为两种疗法效果有差异,该推断犯错误的概率不超过0.05.
?
追问2:根据小概率值????=0.05的独立性检验,分析乙种疗法的效果是否比甲种疗法好.
?
解:
甲种疗法未治愈和治愈的频率分别是????????????????≈????.????????????和????????????????≈????.????????????
乙种疗法未治愈和治愈的频率分别是????????????≈????.????????????和????????????????≈????.0.913.
?
因此可以推断乙种疗法的效果比甲种疗法好。
例4.为了调查吸烟是否对肺癌有影响,某肿瘤研究所采取有放回简单随机抽样,调查了9965人,得到如下结果(单位:人)依据小概率值α=0.001的独立性检验,分析吸烟是否会增加患肺癌的风险。
解:零假设为H0: 吸烟和患肺癌之间没有关系
根据列联表中的数据,经计算得到
2 =
χ
>
根据小概率值α=0.001的独立性检验,推断H0不成立,即认为吸 烟与患肺癌有关联,此推断犯错误的概率不大于0.001,即我们有99.9%的把握认为“吸烟与患肺癌有关系”.
吸烟
肺癌
合计
非肺癌患者
肺癌患者
非吸烟者
7775
42
7817
吸烟者
2099
49
2148
合计
9874
91
9965
根据表中的数据计算不吸烟者中不患肺癌和患肺癌的频率分别为
吸烟者中不患肺癌和患肺癌的频率分别为
由
可见,在被调查者中,吸烟者患肺癌的频率是不吸烟者患肺癌频率的4倍以上。于是,根据频率稳定于概率的原理,我们可以认为吸烟者患肺癌的概率明显大于不吸烟者患肺癌概率,即吸烟更容易引发肺癌。
(1)提出零假设H0:X和Y相互独立,并给出在问题中的解释.
(2)根据抽样数据整理出2×2列联表,计算????????的值,并与临界值????????比较.
(3)根据检验规则得出推断结论.
(4)在X和Y不独立的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
?
应用独立性检验解决实际问题大致应包括以下几个主要环节:
注意:上述几个环节的内容可以根据不同情况进行调整,例如,在有些时候,分类变量的抽样数据列联表是问题中给定的.
六、方法总结
1.某大型企业人力资源部为了研究企业员工工作积极性和对待企业改革态度的关系,经过调查得到如下2×2列联表:
工作态度
对待改革态度
合计
积极支持
不太支持
工作积极
54
40
94
工作一般
32
63
95
合计
86
103
189
能否根据小概率值α=0.005的独立性检验,认为员工工作态度与对待企业改革态度之间有关系?
练习
解:零假设为H0:员工工作态度与对待企业改革态度之间相互独立,即员工工作态度与对待企业改革态度之间无关.
由2×2列联表中的数据,经计算得χ2=189×(54×63?40×32)294×95×86×103≈10.759>7.879=x0.005,因此,根据小概率值α=0.005的独立性检验,我们推断H0不成立,即认为员工工作态度与对待企业改革态度之间有关系,此推断犯错误的概率不大于0.005.
?
2. 某校为调查高中生在校参加体育活动的时间,随机抽取了100名高中生进行调查,其中男女各占一半,如图8-3-1是根据调查结果绘制的学生日均体育锻炼时间的频率分布直方图.
将日均体育锻炼时间不低于40分钟的学生评价
为“良好”,已知“良好”评价中有18名女生.
(1)请将下面的2×2列联表补充完整;
练习
性别
评价
合计
非良好
良好
男生
?
?
?
女生
?
?
?
合计
?
?
?
解:设学生日均体育锻炼时间为x分钟,根据频率分布直方图可知P(x≥40)=(0.025+0.020+0.005)×10=
0.5.抽取总人数为100,
所以评价为“良好”的学生
人数为50.2×2列联表如下:
性别
评价
合计
非良好
良好
男生
18
32
50
女生
32
18
50
合计
50
50
100
(2)根据小概率值α=0.01的独立性检验,分析学生的日均体育锻炼时间与性别是否有关.
解:零假设为H0:学生的日均体育锻炼时间与性别无关,
χ2=????(?????????????????)2(????+????)(????+????)(????+????)(????+????)=100×(18×18?32×32)250×50×50×50=7.84>6.635,
根据小概率值α=0.01的独立性检验,我们推断H0不成立,即认为学生的日均体育锻炼时间与性别有关,此推断犯错误的概率不大于0.01.
?
练习
七、课堂小结
2.独立性检验的一般步骤:
{5940675A-B579-460E-94D1-54222C63F5DA}X
Y
合计
Y=0
Y=1
X=0
a
b
a+b
X=1
c
d
c+d
合计
a+c
b+d
n=a+b+c+d
1.分类变量X和Y的抽样数据的2?2列联表:
(1)提出零假设H0:X和Y相互独立,并给出在问题中的解释.
(2)根据抽样数据整理出2×2列联表,计算????????的值,并与临界值????????比较.
(3)根据检验规则得出推断结论.
(4)在X和Y不独立的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
8.3列联表与独立性检验
一、提出问题
你认为吸烟与患肺癌有关系吗?
怎样用数学知识说明呢?
独立性检验方法
在现实生活中,人们经常需要回答一定范围内的两种现象或性质之间是否存在关联性或互相影响的问题。
例如:就读不同学校是否对学生的成绩有影响,不同班级学生用于体育锻炼的时间是都存在区别,吸烟是否会增加患肺癌的风险等。
分类变量:一种特殊的随机变量,以区别不同的现象或性质
分类变量的取值可以用实数表示,这些数值只作为编号使用,并没有通常的大小和运算意义
举例:
学生所在的班级可以用1,2,3等表示,
男性、女性可以用1,0表示
本节我们主要讨论取值于{0,1}的分类变量的关联性问题.
问题1:为了有针对性地提高学生体育锻炼的积极性,某中学需要了解性别因素是否对本校学生体育锻炼的经常性有影响,为此对学生是否经常锻炼的情况进行了普查.全校生的普查数据如下:523名女生中有331名经常锻炼;601名男生中有473名经常锻。你能利用这些数据,说明该校女生和男生在体育锻炼的经常性方面是否存在差异吗?
比较经常锻炼的学生在女生和男中的比率.
男生经常锻炼的比率比女生高出15.4个百分点,所以该校的女生和男生在体育锻炼的经常性方面有差异,而且男生更经常锻炼。
解法一:
问题1:为了有针对性地提高学生体育锻炼的积极性,某中学需要了解性别因素是否对本校学生体育锻炼的经常性有影响,为此对学生是否经常锻炼的情况进行了普查.全校生的普查数据如下:523名女生中有331名经常锻炼;601名男生中有473名经常锻。你能利用这些数据,说明该校女生和男生在体育锻炼的经常性方面是否存在差异吗?
解法二:
对于Ω中的每一名学生,分别令
性别对体育锻炼的经常性没有影响:
性别对体育锻炼的经常性有影响:
{5940675A-B579-460E-94D1-54222C63F5DA}性别
锻炼
合计
不经常(Y=0)
经常(Y=1)
女生(X=0)
192
331
523
男生(X=1)
128
473
601
合计
320
804
1124
可以做出判断,在该校的学生中,性别对体育锻炼有影响,即该校的女生和男生在体育锻炼的经常性方面存在差异,而且男生更经常锻炼.
二、2×2列联表的概念
{5940675A-B579-460E-94D1-54222C63F5DA}X
Y
合计
Y=0
Y=1
X=0
a
b
a+b
X=1
c
d
c+d
合计
a+c
b+d
n=a+b+c+d
分类变量X和Y的抽样数据的2?2列联表:
用途:可以清晰的给出成对分类变量数据的交叉分类频数。
在上面问题的两种解答中,使用了学校全部学生的调查数据,利用这些数据能够完全确定解答问题所需的比率和条件概率.
然而,对于大多数实际问题,我们无法获得所关心的全部对象的数据,因此无法准确计算出有关的比率或条件概率.
利用随机抽样获得一定数量的样本数据,再利用随机事件发生的频率稳定于概率的原理对问题答案作出推断。
反思
例1:为比较甲、乙两所学校学生的数学水平,采用简单随机抽样的方法抽取88名学生.通过测验得到了如下数据:甲校43名学生中有10名数学成绩优秀;乙校45名学生中有7名数学成绩优秀.试分析两校学生中数学成绩优秀率之间是否存在差异.
解:用Ω表示两所学校的全体学生构成的集合.考虑以Ω为样本空间的古典概型.对于Ω中每一名学生,定义分类变量X和Y如下:
????=????,该生来自甲校,????,该生来自乙校,
?
????=????,该生数学成绩不优秀,????,该生数学成绩优秀。
?
{5940675A-B579-460E-94D1-54222C63F5DA}学校
数学成绩
合计
不优秀(Y=0)
优秀(Y=1)
甲校(X=0)
33
10
43
乙校(X=1)
38
7
45
合计
71
17
88
因此,甲校学生中数学成绩不优秀和数学成绩优秀的频率分别为????????????????≈????.????????????????;????????????????≈????.????????????????;乙校学生中数学成绩不优秀和数学成绩优秀的频率分别为????????????????≈????.????????????????;????????????≈????.????????????????;
?
解:
我们可以用等高堆积条形图直观地展示上述计算结果:
甲校 乙校
通过比较发现,两个学校学生抽样数据中数学成绩优秀的频率存在差异,甲校的频率明显高于乙校的频率.依据频率稳定于概率的原理,我们可以推断那么甲校学生数学成绩优秀的概率大于乙校学生数学成绩优秀的概率。因此,可以认为两校学生的数学成绩优秀率存在差异,甲校学生的数学成绩优秀率比乙校学生的高。
例1:为比较甲、乙两所学校学生的数学水平,采用简单随机抽样的方法抽取88名学生.通过测验得到了如下数据:甲校43名学生中有10名数学成绩优秀;乙校45名学生中有7名数学成绩优秀.试分析两校学生中数学成绩优秀率之间是否存在差异.
因此,甲校学生中数学成绩不优秀和数学成绩优秀的频率分别为????????????????≈????.????????????????;????????????????≈????.????????????????;乙校学生中数学成绩不优秀和数学成绩优秀的频率分别为????????????????≈????.????????????????;????????????≈????.????????????????;
?
(1)频率分析法:通过对样本的每个分类变量的不同类别事件发生的频率大小进行比较来分析分类变量之间是否有关联关系.
如可以通过列联表中????????+????与????????+????值的大小粗略地判断分类变量x和Y之间有无关系.一般其值相差越大,分类变量有关系的可能性越大。
(2)图形分析法:与表格相比,图形更能直观地反映出两个分类变量间是否互相影响,常用等高堆积条形图展示列联表数据的频率特征.将列联表中的数据用高度相同的两个条形图表示出来,其中两列的数据分别对应不同的颜色,这就是等高堆积条形图.
等高堆积条形图可以展示列联表数据的频率特征,能够直观地反映出两个分类变量间是否相互影响。
?
三、两个分类变量之间关联关系的定性分析的方法
问题2:你认为“两校学生的数学成绩优秀率存在差异”这一结论是否有可能是错误的?
答:有可能。
“两校学生的数学成绩优秀率存在差异”这个结论是根据两个频率间存在差异推断出来的.有可能出现这种情况:在随机抽取的这个样本中,两个频率间确实存在差异,但两校学生的数学成绩优秀率实际上是没有差别的.对于随机样本而言,因为频率具有随机性,频率与概率之间存在误差,所以我们的推断可能犯错误,而且在样本容量较小时,犯错误的可能性会较大.因此,需要找到一种更为合理的推断方法,同时也希望能对出现错误推断的概率有一定的控制或估算.
独立性检验方法
练习
1. 在对人们饮食习惯的一次调查中,从某一居民小区中共调查了124位居民,其中六十岁及六十岁以上的70人,六十岁以下的54人.六十岁及六十岁以上的人中有43人的饮食以蔬菜为主,另外27人以肉类为主;六十岁以下的人中有21人的饮食以蔬菜为主,另外33人以肉类为主.请根据以上数据作出饮食习惯与年龄的列联表,并利用P(Y=1|X=0)与P(Y=1|X=1)判断二者是否有关系.
解:用Ω表示调查的124人所构成的集合,对于Ω中的每1位居民,定义一对分类变量X和Y:令X=0,以蔬菜为主,1,以肉类为主,Y=0,六十岁及六十岁以上,1,六十岁以下.
?
用表格整理数据,得到2×2列联表如下:
P(Y=1|X=0)=????(????=0,????=1)????(????=0)=2164≈0.328,
P(Y=1|X=1)=????(????=1,????=1)????(????=1)=3360=0.55.
显然二者具有较为明显的差距,据此可以
在某种程度上认为饮食习惯与年龄有关系.
?
饮食习惯
年龄
合计
六十岁及六十岁以上(Y=0)
六十岁以下(Y=1)
以蔬菜为主(X=0)
43
21
64
以肉类为主(X=1)
27
33
60
合计
70
54
124
2.假设有两个分类变量X与Y,它们的可能取值分别
为X=0,1和Y=0,1,其2×2列联表如下:
若X与Y之间没有影响,则m的值约为 ( )
A.8 B.9 C.14 D.19
?
X
Y
合计
Y=0
Y=1
X=0
10
18
28
X=1
m
26
m+26
合计
10+m
44
m+54
C
练习
3.为了解铅中毒病人与尿棕色素为阳性是否有关系,分别对病人组和对照组的尿液进行尿棕色素定性检查,结果如下:
试画出等高堆积条形图,分析铅中毒病人
与尿棕色素为阳性是否有关系.
分组
尿液定性
合计
阳性(Y=0)
阴性(Y=1)
病人组(X=0)
29
7
36
对照组(X=1)
9
28
37
合计
38
35
73
练习
解:病人组中尿棕色素为阳性和阴性的
频率分别为2936≈0.805 6和736≈0.194 4.
对照组中尿棕色素为阳性和阴性的频率分别为937≈0.243 2和2837≈0.756 8.
等高堆积条形图如图所示.其中两个深色条的高分别
代表铅中毒病人和对照组样本中尿棕色素为阳性的
频率.由图可以直观地看出铅中毒病人与对照组相比,
尿棕色素为阳性的频率差异明显,因此铅中毒病人与
尿棕色素为阳性有关系.
?
8.3.2 独立性检验
8.3列联表与独立性检验
提出零假设(原假设)H0:分类变量X和Y独立.
假定我们通过简单随机抽样得到了X和Y的抽样数据列联表,在列联表中,如果零假设H0成立,则应满足????????+????≈????????+????,即ad-bc≈0.因此,|?????????????????|越小,说明两个分类变量之间关系越弱;|?????????????????|越大,说明两个分类变量之间关系越强.
为了使不同样本容量的数据有统一的评判标准,基于上述分析,我们构造一个随机变量
?
用????????取值的大小作为判断零假设H0是否成立的依据,当它比较大时推断H0不成立,否则认为H0成立。这种利用????????的取值推断分类变量X和Y是否独立的方法称为????????独立性检验,读作“卡方独立性检验”,简称独立性检验.
?
????????=????(?????????????????)????(????+????)(????+????)(????+????)(????+????)
?
四、独立性检验公式及定义
对于任何小概率值????,可以找到相应的正实数????????,使得P(x≥????????)=????成立,我们称????????为????的临界值,这个临界值可作为判断????????大小的标准,概率值????越小,临界值????????越大.
?
{5940675A-B579-460E-94D1-54222C63F5DA}
0.1
0.05
0.01
0.005
0.001
2.706
3.841
6.635
7.879
10.828
基于小概率值????的检验规则:
?
当????????≥????????时,我们就推断H0不成立,即认为X和Y不独立,该推断犯错误的概率不超过????;
当?????????
????????独立性检验中几个常用的小概率值和相应的临界值
?
五、临界值的定义
例2:依据小概率值????=0.1的????????独立性检验,分析例1中的抽样数据,能否据此推
断两校学生的数学成绩优秀率有差异?
?
例1:为比较甲、乙两所学校学生的数学水平,采用简单随机抽样的方法抽取88名学生.通过测验得到了如下数据:甲校43名学生中有10名数学成绩优秀;乙校45名学生中有7名数学成绩优秀.试分析两校学生中数学成绩优秀率之间是否存在差异.
解:零假设为H0:分类变量X与Y相互独立,即两校学生的数学成绩优秀率无差异.
{5940675A-B579-460E-94D1-54222C63F5DA}学校
数学成绩
合计
不优秀(Y=0)
优秀(Y=1)
甲校(X=0)
33
10
43
乙校(X=1)
38
7
45
合计
71
17
88
所以
????????=????????(????????×?????????????×????????)????????????×????????×????????×????????≈????.?????????????
根据小概率值????=0.1的????????独立性检验,没有充分证据推断H0不成立,因此可以认为H0成立,即认为两校的数学成绩优秀率没有差异。
?
思考:例1和例2都是基于同一组数据的分析,但却得出了不同的结论,你能说明其中的原因吗?
例1只是根据一个样本的两个频率间存在差异得出两校学生数学成绩优秀率有差异的结论,并没有考虑由样本随机性可能导致的错误,所以那里的推断依据不太充分。
在例2中,我们用????????独立性检验对零假设H0进行了检验,通过计算,发现????????≈0.837小于α=0.1所对应的临界值2.706,因此认为没有充分证据推断H0不成立,所以接受H0,推断出两校学生的数学优秀率没有显著差异的结论,
这个检验结果意味着,抽样数据中两个频率的差异很有可能是由样本随机性导致的,因此,只根据频率的差异得出两校学生的数学成绩优秀率有差异的结论是不可靠的。
由此可见,相对于简单比较两个频率的推断,用????????独立性检验得到的结果更理性、更全面,理论依据也更充分。
?
当我们接受零假设H0时,也可能犯错误。我们不知道犯这类错误的概率p的大小,但是知道,若α越大,则p越小
例3:某儿童医院用甲、乙两种疗法治疗小儿消化不良.采用有放回简单随机抽样的方法对治疗情况进行检查,得到了如下数据:抽到接受甲种疗法的患儿67名,其中未治愈15名,治愈52名;抽到接受乙种疗法的患儿69名,其中未治愈6名,治愈63名.试根据小概率值????=0.005的独立性检验,分析乙种疗法的效果是否比甲种疗法好.
?
解:零假设为H0:疗法与疗效独立,即两种疗法效果没有差异.
将所给数据进行整理,得到两种疗法治疗数据的列联表,
{5940675A-B579-460E-94D1-54222C63F5DA}疗法
疗效
合计
未治愈
治愈
甲
15
52
67
乙
6
63
69
合计
21
115
136
根据列联表中的数据,经计算得到????????=????????????×(????????×?????????????????×????)????????????×????????×????????×????????????≈????.?????????????
根据小概率值????=0.005的????????独立性检验,没有充分证据推断 H0不成立,因此可以认为 H0成立,即认为两种疗法效果没有差异.
?
追问1:若对调两种疗法的位置或对调两种疗效的位置,这样做会影响????????取值的计算结果吗?
?
不影响
{5940675A-B579-460E-94D1-54222C63F5DA}疗法
疗效
合计
未治愈
治愈
甲
15
52
67
乙
6
63
69
合计
21
115
136
{5940675A-B579-460E-94D1-54222C63F5DA}疗法
疗效
合计
未治愈
治愈
乙
6
63
69
甲
15
52
67
合计
21
115
136
{5940675A-B579-460E-94D1-54222C63F5DA}疗法
疗效
合计
治愈
未治愈
甲
52
15
67
乙
63
6
69
合计
115
21
136
????????=????????????×(????????×?????????????????×????)????????????×????????×????????×????????????≈????.????????????
?
????????=????????????×(????????×?????????????×????????)????????????×????????×????????×????????????≈????.????????????
?
????????=????????????×(????????×?????????????×????????)????????????×????????×????????×????????????≈????.????????????
?
追问2:根据小概率值????=0.05的独立性检验,分析乙种疗法的效果是否比甲种疗法好.
?
解:零假设为H0:疗法与疗效独立,即两种疗法效果没有差异.
将所给数据进行整理,得到两种疗法治疗数据的列联表,
{5940675A-B579-460E-94D1-54222C63F5DA}疗法
疗效
合计
未治愈
治愈
甲
15
52
67
乙
6
63
69
合计
21
115
136
根据列联表中的数据,经计算得到????????=????????????×(????????×?????????????????×????)????????????×????????×????????×????????????≈????.????????????>????.????????????=????????.????????.
?
根据小概率值????=0.05的????????独立性检验,我们推断 H0不成立,即可以认为两种疗法效果有差异,该推断犯错误的概率不超过0.05.
?
追问2:根据小概率值????=0.05的独立性检验,分析乙种疗法的效果是否比甲种疗法好.
?
解:
甲种疗法未治愈和治愈的频率分别是????????????????≈????.????????????和????????????????≈????.????????????
乙种疗法未治愈和治愈的频率分别是????????????≈????.????????????和????????????????≈????.0.913.
?
因此可以推断乙种疗法的效果比甲种疗法好。
例4.为了调查吸烟是否对肺癌有影响,某肿瘤研究所采取有放回简单随机抽样,调查了9965人,得到如下结果(单位:人)依据小概率值α=0.001的独立性检验,分析吸烟是否会增加患肺癌的风险。
解:零假设为H0: 吸烟和患肺癌之间没有关系
根据列联表中的数据,经计算得到
2 =
χ
>
根据小概率值α=0.001的独立性检验,推断H0不成立,即认为吸 烟与患肺癌有关联,此推断犯错误的概率不大于0.001,即我们有99.9%的把握认为“吸烟与患肺癌有关系”.
吸烟
肺癌
合计
非肺癌患者
肺癌患者
非吸烟者
7775
42
7817
吸烟者
2099
49
2148
合计
9874
91
9965
根据表中的数据计算不吸烟者中不患肺癌和患肺癌的频率分别为
吸烟者中不患肺癌和患肺癌的频率分别为
由
可见,在被调查者中,吸烟者患肺癌的频率是不吸烟者患肺癌频率的4倍以上。于是,根据频率稳定于概率的原理,我们可以认为吸烟者患肺癌的概率明显大于不吸烟者患肺癌概率,即吸烟更容易引发肺癌。
(1)提出零假设H0:X和Y相互独立,并给出在问题中的解释.
(2)根据抽样数据整理出2×2列联表,计算????????的值,并与临界值????????比较.
(3)根据检验规则得出推断结论.
(4)在X和Y不独立的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
?
应用独立性检验解决实际问题大致应包括以下几个主要环节:
注意:上述几个环节的内容可以根据不同情况进行调整,例如,在有些时候,分类变量的抽样数据列联表是问题中给定的.
六、方法总结
1.某大型企业人力资源部为了研究企业员工工作积极性和对待企业改革态度的关系,经过调查得到如下2×2列联表:
工作态度
对待改革态度
合计
积极支持
不太支持
工作积极
54
40
94
工作一般
32
63
95
合计
86
103
189
能否根据小概率值α=0.005的独立性检验,认为员工工作态度与对待企业改革态度之间有关系?
练习
解:零假设为H0:员工工作态度与对待企业改革态度之间相互独立,即员工工作态度与对待企业改革态度之间无关.
由2×2列联表中的数据,经计算得χ2=189×(54×63?40×32)294×95×86×103≈10.759>7.879=x0.005,因此,根据小概率值α=0.005的独立性检验,我们推断H0不成立,即认为员工工作态度与对待企业改革态度之间有关系,此推断犯错误的概率不大于0.005.
?
2. 某校为调查高中生在校参加体育活动的时间,随机抽取了100名高中生进行调查,其中男女各占一半,如图8-3-1是根据调查结果绘制的学生日均体育锻炼时间的频率分布直方图.
将日均体育锻炼时间不低于40分钟的学生评价
为“良好”,已知“良好”评价中有18名女生.
(1)请将下面的2×2列联表补充完整;
练习
性别
评价
合计
非良好
良好
男生
?
?
?
女生
?
?
?
合计
?
?
?
解:设学生日均体育锻炼时间为x分钟,根据频率分布直方图可知P(x≥40)=(0.025+0.020+0.005)×10=
0.5.抽取总人数为100,
所以评价为“良好”的学生
人数为50.2×2列联表如下:
性别
评价
合计
非良好
良好
男生
18
32
50
女生
32
18
50
合计
50
50
100
(2)根据小概率值α=0.01的独立性检验,分析学生的日均体育锻炼时间与性别是否有关.
解:零假设为H0:学生的日均体育锻炼时间与性别无关,
χ2=????(?????????????????)2(????+????)(????+????)(????+????)(????+????)=100×(18×18?32×32)250×50×50×50=7.84>6.635,
根据小概率值α=0.01的独立性检验,我们推断H0不成立,即认为学生的日均体育锻炼时间与性别有关,此推断犯错误的概率不大于0.01.
?
练习
七、课堂小结
2.独立性检验的一般步骤:
{5940675A-B579-460E-94D1-54222C63F5DA}X
Y
合计
Y=0
Y=1
X=0
a
b
a+b
X=1
c
d
c+d
合计
a+c
b+d
n=a+b+c+d
1.分类变量X和Y的抽样数据的2?2列联表:
(1)提出零假设H0:X和Y相互独立,并给出在问题中的解释.
(2)根据抽样数据整理出2×2列联表,计算????????的值,并与临界值????????比较.
(3)根据检验规则得出推断结论.
(4)在X和Y不独立的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
