沪科版九年级上册 22.3 相似三角形的性质 教案
文档属性
| 名称 | 沪科版九年级上册 22.3 相似三角形的性质 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 335.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 00:00:00 | ||
图片预览



文档简介
相似三角形的性质(第一课时)
教学目标:
1、知识与技能:掌握相似形三角形的对应高、中线、角平分线的比、周长的比都等于相似比的性质,并能利用相似形的相关性质解决一些简单的问题。
2、过程与方法:通过相似三角形的性质的探索,以知识的逐渐深化推动学生的学习,并引导学生得出正确的结论,用之解决实际问题;学会观察、类比和概括,增强动手操作和独立思考的能力;
3、情感与态度:
(1)通过全等三形与相似三角形的类比学习,树立学生从特殊到一般的认识规律。
(2)通过先实验后归纳推理得出性质定理,强化学生“实践出真知”的求知意识。
教学重难点
重点:1、相似三角形中对应线段比值的推导;
2、运用相似三角形的性质解决实际问题。
难点:相似三角形的性质的运用。
教学方法 :引导启发式,实验探讨法
教学过程设计
一.创设情境、导入新课
故事情境:(图片展示埃及金字塔)
古希腊有一位数学家泰勒斯到埃及游学,一天,泰勒斯与他的弟子们,还有一些埃及贵族,坐在金字塔的阴影中谈论着一些琐事。
一位贵族想戏弄一下泰勒斯,对泰勒斯说到:“亲爱的泰勒斯先生,到埃及的日子也不短了,有什么收获呢?总不能空手而归吧?”
泰勒斯从容不从容不迫的答道:“亲爱的先生们,我们或许追求不同,也许你喜欢金钱,也许你喜欢女人,而我则不同,只以追求科学知识为光荣。”
泰勒斯继续说到:“我到埃及游学,学到了很多知识,并把几何提到了证明的理论高度,并给予证明”。
贵族说到:“您的那些东西,又有什么用呢?它能算出金字塔的高吗?”
泰勒斯并没有立即想出办法来:“怎样测出金字塔的高度,让我回家好好想一想,五天后见。”
五天后,泰勒斯果然解决了这个问题。
泰勒斯是运用什么知识解决这一问题的呢?通过今天这堂课的学习,我们将为同学们揭密。
课题:相似三角形的性质
二、师生合作、探究新知
1、阅读课本P78内容
找一找,猜猜看,泰勒斯是用到我们课本上相似形三角形的哪一个性质?
(相似三角形对应高的比等于相似比)
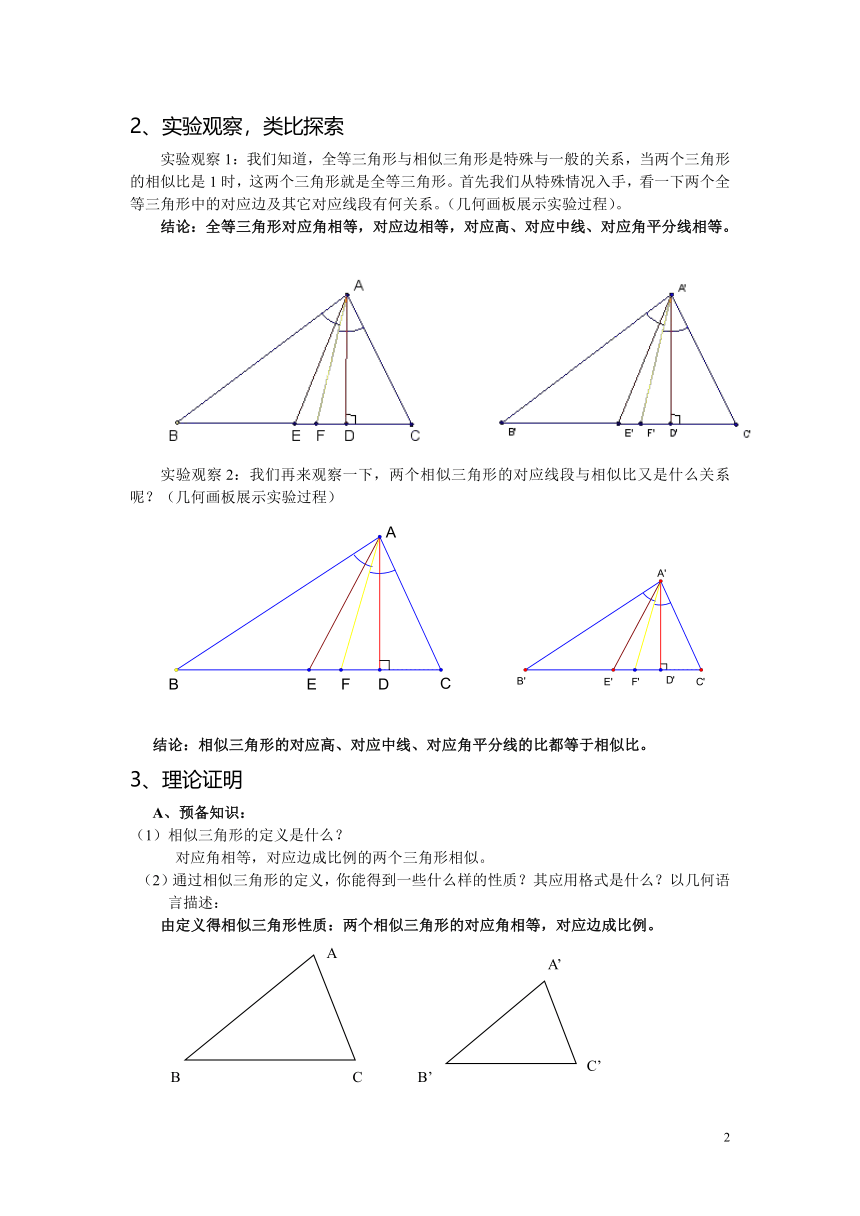
2、实验观察,类比探索
实验观察1:我们知道,全等三角形与相似三角形是特殊与一般的关系,当两个三角形的相似比是1时,这两个三角形就是全等三角形。首先我们从特殊情况入手,看一下两个全等三角形中的对应边及其它对应线段有何关系。(几何画板展示实验过程)。
结论:全等三角形对应角相等,对应边相等,对应高、对应中线、对应角平分线相等。
实验观察2:我们再来观察一下,两个相似三角形的对应线段与相似比又是什么关系呢?(几何画板展示实验过程)
结论:相似三角形的对应高、对应中线、对应角平分线的比都等于相似比。
3、理论证明
A、预备知识:
(1)相似三角形的定义是什么?
对应角相等,对应边成比例的两个三角形相似。
(2)通过相似三角形的定义,你能得到一些什么样的性质?其应用格式是什么?以几何语言描述:
由定义得相似三角形性质:两个相似三角形的对应角相等,对应边成比例。
∵ΔABC∽ΔA′B′C′,
∴∠A=∠A′,∠B=∠B′,∠C=∠C′
(3)什么叫相似比?
相似三角形对应边的比。
(4)相似三角形的判定定理有哪些?
、两角对应相等的两个三角形相似。
、两边对应成比例且夹角相等的两个三角形相似。
、三边对应成比例的两个三角形相似。
、一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
B、理论证明:
下面,我们以相似三角形对应边上的高的比等于相似比为例,证明如下 :
已知:如图ΔABC∽ΔA′B′C′,它们的相似比为k,AD、A′D′是对应高,求证:.
分析:
在这里要通过三角形相似去证比例式,先要看所证的比例式在哪两个三角形中,在这里是在ΔABD与ΔA′B′D′中,只需要证这两个三角形相似即可。再想想:要证这两个三角形相似,具备了哪些条件,还差哪些条件?(师生共同完成证明过程)
证明:∵ ΔABC∽ΔA′B′C′,
∴ ∠B=∠B‘
又 ∵ ∠BDA=∠B′D′A′=90°
∴ RtΔABD∽RtΔA′B′D′
∴ .
C、举一反三
同学们仿照上面的证明,自己来证明另外两个结论。
已知:如图ΔABC∽ΔA′B′C′,它们的相似比为k,AD、A′D′是对应中线(或对应角平线),求证:
1、证明 ∵ △ABC∽ △A′B′C′
∴∠B=∠B’
又∵AD,A‘D’分别是BC和B‘C’边上的中线
∴ ∴
∴ △ABD∽ △A′B′D′ ∴
2、证明 ∵ △ABC∽ △A′B′C′
∴∠B=∠B’ ∠BAC=∠B’A’C’
又 ∵AD,A’D’分别是∠BAC和∠B’A’C’的角平分线
∴
即:∠BAD=∠B’A’D’
∴ △ABD∽ △A′B′D′
∴
4、结论: 定理1:
相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比。
三、定理1的应用
应用1、填空:
(1)两个相似三角形的对应边的比为3:4,则这两个三角形的对应角平分线的比为_____ ,对应边上的高的比为____,对应边上的中线的比为____
(2)相似三角形对应角平分线比为0.2,则相似比为_________,对应中线的比等于______;
应用2: 已知ΔABC∽ΔA′B′C′, BC=3.6cm,B’C’=6cm,AE是ΔABC的一条中线,AE=2.4cm,求ΔA′B′C′中对应中线A’E’的长
应用3:揭密泰勒斯测量金字塔的方法:
泰勒斯为了测量金字塔的高度AD,先竖一根已知长度的木棒A′D′,比较棒子的影长B′D′与金字塔的影长BD,即可近似算出金字塔的高度AD.
金字塔的高度和影长组成的三角形相似于木棒高和影长组成的三角形
再利用相似三角形对应高的比等于相似比(或相似三角形对应边成比例)来求解.
即:
如果我们知道你个人的身高和步长,便可代替木棒和皮尺,也能求出某建筑物的高度,方法更简便。
应用4:步枪在瞄准时的示意图如图,从眼睛到准星的距离OE为80cm,步枪上准星宽度AB为2mm,目标的正面宽度CD为50cm,求眼睛到目标的距离OF。
解:由题意知:AB∥CD
∴ △OAB∽△OCD
又 ∵ OE⊥AB,OF⊥CD
∴ ∴
∴ OF=2000(cm)=20(m)
答:眼睛到目标的距离OF为20m
四、定理1的拓展
(几何画板演示)
1、如图所示,如果ΔABC∽ΔA′B′C′, D是BC边上的点,且;D′是B′C′边上的点,且,若,试说明:。
2、把A、A′分别沿AB、A′B′移动到E、E′的位置,则有:
如图所示,如果ΔABC∽ΔA′B′C′, D是BC边上的点,且;D′是B′C′边上的点,且;E点在AB上,且AE=AB;点E′在A′B′上,且,且有,试说明:。
结论:相似三角形一切对应线段的比等于相似比。
五、定理2:
相似三角形的周长的比等于相似比
已知:如图ΔABC∽ΔA′B′C′,且它们的相似比为k,
则有:,由等比性质,得。
六、本课总结
1、从知识面上看:
今天我们学习相似三角形哪些性质?
(1) 相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比。
相似三角形一切对应线段的比都等于相似比
(2) 相似三角形周长的比等于相似比
放大0次量(角度)、一次量(线段)、二次量(面积)、三次量(体积)
2、从学习方法上看:
(1)类比思考、实验探索,
(2)掌握认识事物、探究新知可以从特殊到一般的认知规律
七:作业
习题
第1、5、6题
教学设计思路
相似三角形的性质这一节内容,从教学要求上看,共安排三个课时,本节课是第一课时,本课教学知识点主要是两个定理及它的简单应用。
我认为第一课时应安排为一次量的变换,即线段的比、周长的比;第二课时安排为二次量或三次量的变换,即面积比和体积比;第三课时安排为性质的综合运用。
本节课在知识的传授过程中,我并没有急于要求同学们去证明性质定理,而是从古代数学家泰勒斯的故事引入,抓住同学们想知道数学家是怎么完成金字塔的测量的心理,去阅读教材,寻求答案。在同学们猜得答案的同时,正是我们寻找它理论依据的时机。
大家知道,新课程改革中要求我们重视以前被忽视的过程与方法、情感态度和价值观的培养,所以我在知识的教学中,先通过实验操作,有意识地带领同学们去经历这种探索和发现的过程,学会思考问题的方法。如,类比思考,从特殊到一般的认知规律等等。类比主要体现在全等与相似的类比,还有性质1中,由相似三角形对应高的比等于相似比,去类比证明对应中线,对应角平分线的比也等于相似比,再类比证明相似三角形一切对应线段的比都等于相似比。从而完成了由“实验几何”到“论证几何”的过程。
在发展能力方面,我注重了性质定理的运用和拓展。通过列举实例,强调应用。在拓展性质时,把众多的结论归结为一个定理,即相似三角形的一切对应线段的比都等于相似比,这不但使我们记忆负担减轻了,更重要的是使我们的认识更深刻了,让同学们站在一个系统的高度认识问题。
在例题的安排上,考虑三点:1、熟悉定理 2、注意性质定理的应用格式 3、运用定理解决问题。
最后总结时,从两个方面去归纳,一是知识层面,二是数学思想方法。让学生学有所思。
当然,教无定法,教学过程中,也一定存在不足之处,欢迎各位同行提出宝贵意见。以便共同学习共同提高。
A
B
C
A’‘
B’
C’
E
A
B
O
C
D
F
A
B
C
A’‘
B’
C’
PAGE
1
教学目标:
1、知识与技能:掌握相似形三角形的对应高、中线、角平分线的比、周长的比都等于相似比的性质,并能利用相似形的相关性质解决一些简单的问题。
2、过程与方法:通过相似三角形的性质的探索,以知识的逐渐深化推动学生的学习,并引导学生得出正确的结论,用之解决实际问题;学会观察、类比和概括,增强动手操作和独立思考的能力;
3、情感与态度:
(1)通过全等三形与相似三角形的类比学习,树立学生从特殊到一般的认识规律。
(2)通过先实验后归纳推理得出性质定理,强化学生“实践出真知”的求知意识。
教学重难点
重点:1、相似三角形中对应线段比值的推导;
2、运用相似三角形的性质解决实际问题。
难点:相似三角形的性质的运用。
教学方法 :引导启发式,实验探讨法
教学过程设计
一.创设情境、导入新课
故事情境:(图片展示埃及金字塔)
古希腊有一位数学家泰勒斯到埃及游学,一天,泰勒斯与他的弟子们,还有一些埃及贵族,坐在金字塔的阴影中谈论着一些琐事。
一位贵族想戏弄一下泰勒斯,对泰勒斯说到:“亲爱的泰勒斯先生,到埃及的日子也不短了,有什么收获呢?总不能空手而归吧?”
泰勒斯从容不从容不迫的答道:“亲爱的先生们,我们或许追求不同,也许你喜欢金钱,也许你喜欢女人,而我则不同,只以追求科学知识为光荣。”
泰勒斯继续说到:“我到埃及游学,学到了很多知识,并把几何提到了证明的理论高度,并给予证明”。
贵族说到:“您的那些东西,又有什么用呢?它能算出金字塔的高吗?”
泰勒斯并没有立即想出办法来:“怎样测出金字塔的高度,让我回家好好想一想,五天后见。”
五天后,泰勒斯果然解决了这个问题。
泰勒斯是运用什么知识解决这一问题的呢?通过今天这堂课的学习,我们将为同学们揭密。
课题:相似三角形的性质
二、师生合作、探究新知
1、阅读课本P78内容
找一找,猜猜看,泰勒斯是用到我们课本上相似形三角形的哪一个性质?
(相似三角形对应高的比等于相似比)
2、实验观察,类比探索
实验观察1:我们知道,全等三角形与相似三角形是特殊与一般的关系,当两个三角形的相似比是1时,这两个三角形就是全等三角形。首先我们从特殊情况入手,看一下两个全等三角形中的对应边及其它对应线段有何关系。(几何画板展示实验过程)。
结论:全等三角形对应角相等,对应边相等,对应高、对应中线、对应角平分线相等。
实验观察2:我们再来观察一下,两个相似三角形的对应线段与相似比又是什么关系呢?(几何画板展示实验过程)
结论:相似三角形的对应高、对应中线、对应角平分线的比都等于相似比。
3、理论证明
A、预备知识:
(1)相似三角形的定义是什么?
对应角相等,对应边成比例的两个三角形相似。
(2)通过相似三角形的定义,你能得到一些什么样的性质?其应用格式是什么?以几何语言描述:
由定义得相似三角形性质:两个相似三角形的对应角相等,对应边成比例。
∵ΔABC∽ΔA′B′C′,
∴∠A=∠A′,∠B=∠B′,∠C=∠C′
(3)什么叫相似比?
相似三角形对应边的比。
(4)相似三角形的判定定理有哪些?
、两角对应相等的两个三角形相似。
、两边对应成比例且夹角相等的两个三角形相似。
、三边对应成比例的两个三角形相似。
、一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
B、理论证明:
下面,我们以相似三角形对应边上的高的比等于相似比为例,证明如下 :
已知:如图ΔABC∽ΔA′B′C′,它们的相似比为k,AD、A′D′是对应高,求证:.
分析:
在这里要通过三角形相似去证比例式,先要看所证的比例式在哪两个三角形中,在这里是在ΔABD与ΔA′B′D′中,只需要证这两个三角形相似即可。再想想:要证这两个三角形相似,具备了哪些条件,还差哪些条件?(师生共同完成证明过程)
证明:∵ ΔABC∽ΔA′B′C′,
∴ ∠B=∠B‘
又 ∵ ∠BDA=∠B′D′A′=90°
∴ RtΔABD∽RtΔA′B′D′
∴ .
C、举一反三
同学们仿照上面的证明,自己来证明另外两个结论。
已知:如图ΔABC∽ΔA′B′C′,它们的相似比为k,AD、A′D′是对应中线(或对应角平线),求证:
1、证明 ∵ △ABC∽ △A′B′C′
∴∠B=∠B’
又∵AD,A‘D’分别是BC和B‘C’边上的中线
∴ ∴
∴ △ABD∽ △A′B′D′ ∴
2、证明 ∵ △ABC∽ △A′B′C′
∴∠B=∠B’ ∠BAC=∠B’A’C’
又 ∵AD,A’D’分别是∠BAC和∠B’A’C’的角平分线
∴
即:∠BAD=∠B’A’D’
∴ △ABD∽ △A′B′D′
∴
4、结论: 定理1:
相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比。
三、定理1的应用
应用1、填空:
(1)两个相似三角形的对应边的比为3:4,则这两个三角形的对应角平分线的比为_____ ,对应边上的高的比为____,对应边上的中线的比为____
(2)相似三角形对应角平分线比为0.2,则相似比为_________,对应中线的比等于______;
应用2: 已知ΔABC∽ΔA′B′C′, BC=3.6cm,B’C’=6cm,AE是ΔABC的一条中线,AE=2.4cm,求ΔA′B′C′中对应中线A’E’的长
应用3:揭密泰勒斯测量金字塔的方法:
泰勒斯为了测量金字塔的高度AD,先竖一根已知长度的木棒A′D′,比较棒子的影长B′D′与金字塔的影长BD,即可近似算出金字塔的高度AD.
金字塔的高度和影长组成的三角形相似于木棒高和影长组成的三角形
再利用相似三角形对应高的比等于相似比(或相似三角形对应边成比例)来求解.
即:
如果我们知道你个人的身高和步长,便可代替木棒和皮尺,也能求出某建筑物的高度,方法更简便。
应用4:步枪在瞄准时的示意图如图,从眼睛到准星的距离OE为80cm,步枪上准星宽度AB为2mm,目标的正面宽度CD为50cm,求眼睛到目标的距离OF。
解:由题意知:AB∥CD
∴ △OAB∽△OCD
又 ∵ OE⊥AB,OF⊥CD
∴ ∴
∴ OF=2000(cm)=20(m)
答:眼睛到目标的距离OF为20m
四、定理1的拓展
(几何画板演示)
1、如图所示,如果ΔABC∽ΔA′B′C′, D是BC边上的点,且;D′是B′C′边上的点,且,若,试说明:。
2、把A、A′分别沿AB、A′B′移动到E、E′的位置,则有:
如图所示,如果ΔABC∽ΔA′B′C′, D是BC边上的点,且;D′是B′C′边上的点,且;E点在AB上,且AE=AB;点E′在A′B′上,且,且有,试说明:。
结论:相似三角形一切对应线段的比等于相似比。
五、定理2:
相似三角形的周长的比等于相似比
已知:如图ΔABC∽ΔA′B′C′,且它们的相似比为k,
则有:,由等比性质,得。
六、本课总结
1、从知识面上看:
今天我们学习相似三角形哪些性质?
(1) 相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比。
相似三角形一切对应线段的比都等于相似比
(2) 相似三角形周长的比等于相似比
放大0次量(角度)、一次量(线段)、二次量(面积)、三次量(体积)
2、从学习方法上看:
(1)类比思考、实验探索,
(2)掌握认识事物、探究新知可以从特殊到一般的认知规律
七:作业
习题
第1、5、6题
教学设计思路
相似三角形的性质这一节内容,从教学要求上看,共安排三个课时,本节课是第一课时,本课教学知识点主要是两个定理及它的简单应用。
我认为第一课时应安排为一次量的变换,即线段的比、周长的比;第二课时安排为二次量或三次量的变换,即面积比和体积比;第三课时安排为性质的综合运用。
本节课在知识的传授过程中,我并没有急于要求同学们去证明性质定理,而是从古代数学家泰勒斯的故事引入,抓住同学们想知道数学家是怎么完成金字塔的测量的心理,去阅读教材,寻求答案。在同学们猜得答案的同时,正是我们寻找它理论依据的时机。
大家知道,新课程改革中要求我们重视以前被忽视的过程与方法、情感态度和价值观的培养,所以我在知识的教学中,先通过实验操作,有意识地带领同学们去经历这种探索和发现的过程,学会思考问题的方法。如,类比思考,从特殊到一般的认知规律等等。类比主要体现在全等与相似的类比,还有性质1中,由相似三角形对应高的比等于相似比,去类比证明对应中线,对应角平分线的比也等于相似比,再类比证明相似三角形一切对应线段的比都等于相似比。从而完成了由“实验几何”到“论证几何”的过程。
在发展能力方面,我注重了性质定理的运用和拓展。通过列举实例,强调应用。在拓展性质时,把众多的结论归结为一个定理,即相似三角形的一切对应线段的比都等于相似比,这不但使我们记忆负担减轻了,更重要的是使我们的认识更深刻了,让同学们站在一个系统的高度认识问题。
在例题的安排上,考虑三点:1、熟悉定理 2、注意性质定理的应用格式 3、运用定理解决问题。
最后总结时,从两个方面去归纳,一是知识层面,二是数学思想方法。让学生学有所思。
当然,教无定法,教学过程中,也一定存在不足之处,欢迎各位同行提出宝贵意见。以便共同学习共同提高。
A
B
C
A’‘
B’
C’
E
A
B
O
C
D
F
A
B
C
A’‘
B’
C’
PAGE
1
