沪科版七年级数学8.3完全平方公式与平方差公式(第4课时)整式乘法综合练习 课件 (共26张PPT)
文档属性
| 名称 | 沪科版七年级数学8.3完全平方公式与平方差公式(第4课时)整式乘法综合练习 课件 (共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 359.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 20:11:19 | ||
图片预览








文档简介
(共26张PPT)
沪科版数学七年级下
8.3 完全平方公式与平方差公式
第4课时 整式的乘除综合练习
一、整式乘除 法则回顾
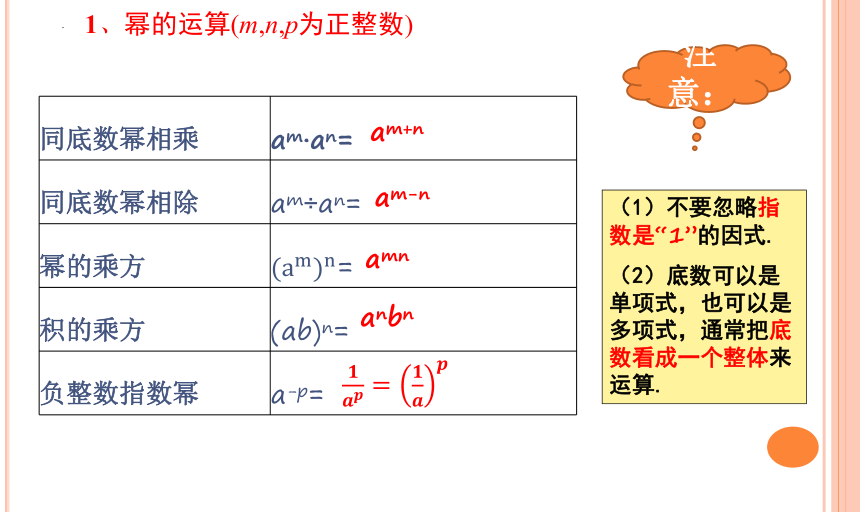
同底数幂相乘 am·an=
同底数幂相除 am÷an=
幂的乘方 =
积的乘方 (ab)n=
负整数指数幂 a-p=
am+n
am-n
amn
anbn
1、幂的运算(m,n,p为正整数)
(1)不要忽略指数是“1”的因式.
(2)底数可以是单项式,也可以是多项式,通常把底数看成一个整体来运算.
注 意:
2、整式乘法运算
单项式乘单项式
单项式乘多项式
多项式乘多项式
乘法公式
把系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数 作为积的一个因式
m(a+b)=ma+mb
(m+n)(a+b)
=m(a+b)+n(a+b)
=ma+mb+na+nb
平方差公式: (a+b)(a-b)=a2-b2
完全平方公式: (a±b)2=a2±2ab+b2
3、整式除法运算
单项式除 以单项式
多项式除 以单项式
把系数、同底数幂分别相除,作为商的因式,对于只在被除式中含有的字母,则连同它的指数作为商的一个因式
先把这个多项式的每一项除以这个单项式,再把所得的商相加.
二、整式乘除常见题型例题选讲
1、下列运算正确的是( )
A.(a2)3=a5 B.a2·a4=a8 C.a6÷a3=a2 D.(ab)3=a3b3
2、计算(-a3)2的结果是( )
A.a6 B. -a6 C. -a5 D.a5
3、计算a10÷a2(a≠0)的结果是 ( )
A.a5 B.a-5 C.a8 D.a-8
4、x2·x3=( )
A.x5 B.x6 C.x8 D.x9
一、选择题
D
A
A
幂的运算法则要记忆正确
C
5、小明总结以下结论:①a(b+c)=ab+ac;②a (b+c)=ab-ac;③(b-c)÷a=b÷a-c÷a;④a÷(b+c)=a÷b+a÷c.其中一定成立的个数是( )
A.1 B.2 C.3 D.4
C
6、计算(2x)3÷x的结果正确的是( )
A.8x2 B.6x2 C.8x3 D.6x3
A
7、下列计算正确的是( )
A.a4+a5=a9 B.(2a2b3)2=4a4b6
C.-2a(a+3)=-2a2+6a D.(2a-b)2=4a2-b2
B
混合运算时要注意运算顺序
8、已知4m=a,8n=b,其中m,n为正整数,则22m+6n=( )
A.ab2 B.a+b2 C.a2b3 D.a2+b3
幂的运算法则逆用:
amn=(am)n=(an)m
解:∵4m=a,8n=b
∴22m=a,23n=b
∴22m+6n= 22m×26n= 22m×(23n)2 =ab
A
10、计算(a-2)(a+3)的结果是( )
A.a2-6 B.a2+a-6 C.a2+6 D.a2-a+6
9、化简(x-3)2-x(x-6)的结果为( )
A.6x-9 B.-12x+9 C.9 D.3x+9
解:原式=x2-6x+9-x2+6x=9
C
B
12、下列计算结果为2ab–a2–b2的是( )
A.(a–b)2 B.(–a–b)2
C.–(a+b)2 D.–(a–b)2
11、运用乘法公式计算(a–2)2的结果是( )
A.a2–4a+4 B.a2–2a+4
C.a2–4 D.a2–4a–4
A
D
13、将9.52变形正确的是( )
A.9.52=92+0.52 B.9.52=(10+0.5)(10–0.5)
C.9.52=102–2×10×0.5+0.52 D.9.52=92+9×0.5+0.52
C
14、下列运算中,可用平方差公式计算的是( )
A.(x+y)(x+y) B.(–x+y)(x–y)
C.(–x–y)(y–x) D.(x+y)(–x–y)
C
15、计算(2x+1)(2x–1)等于( )
A.4x2–1 B.2x2–1 C.4x–1 D.4x2+1
A
15
二、填空题
1、若2x=3,2y=5,则2x+y= .
解:2x+y=2x·2y=3×5=15.
2、已知xy=9,x-y=-3,则x +3xy+y =
解:x +3xy+y =x -2xy+y +5xy =(x-y) + 5xy =54
54
3、计算(x-8)(x +8x+64)=
4、计算(4x)M=12x y3-16x3y +4x y ,则 M=
M=(12x y3-16x3y +4x y )÷(4x)=3xy -4x y+xy
3xy -4x y+xy
x3-512
①
②
③
1、下列各题的解法是否正确,如果错了,指出错在什么地方,并改正过来.
×
×
×
漏了单独字母
漏乘1
符号没有变化
三、法则辨析
2、判别下列解法是否正确,若不正确,请说出理由.
解:原式
漏 乘,少了-3x
解:原式
运算法则混淆
四、计算与化简
1、计算:(1)(x 3y)(x+7y); (2)(2x + 5y)(3x 2y).
(3)(3a+b–2)(3a–b+2); (4)(x–y–m+n)(x–y+m–n).
解:
(1) (x 3y)(x+7y)
+
7xy
3yx
=
x2 +4xy–21y2;
21y2
(2) (2x +5 y)(3x 2y)
=
=x2
2x 3x
2x 2y
+5 y 3x
5y 2y
=
6x2
4xy
+ 15xy
10y2
=
6x2 +11xy 10y2.
(4)原式=[(x–y)–(m–n)][(x–y)+(m–n)]
(3)原式=[3a+(b–2)][3a–(b–2)]
=(3a)2–(b–2)2
=9a2–b2+4b–4.
=(x–y)2–(m–n)2
=x2–2xy+y2–m2+2mn–n2.
2、解方程与不等式:
①(x–3)(x–2)+18=(x+9)(x+1);
②(3x+6)(3x–6)<9(x–2)(x+3).
解:①原式去括号,得:x2–5x+6+18=x2+10x+9,
移项合并,得:15x=15,
解得:x=1;
②原式去括号,得:9x2–36<9x2+9x–54,
移项合并,得:9x>18,
解得:x>2 .
化简过程中尽量用乘法公式进行简便运算
3、先化简,再求值:(a+3)2-(a+1)(a-1)-2(2a+4),其中a= - .
解:原式=a2+6a+9-a2+1-4a-8
=2a+2,
当a=-时,
原式=2×(-)+2
=-1+2
=1.
合并同类项不要漏项
方法总结:熟练掌握完全平方公式的变式:
(1)x2+y2
=(x–y)2+2xy
=(x+y)2–2xy,
(2) (x–y)2
=(x+y)2–4xy.
(3)4xy=(x+y)2–(x–y)2
4、已知(x+y)2=25,(x-y)2=9,求xy与x2+y2的值.
解:∵(x+y)2=25,
∴x2+2xy+y2=25.①
∵(x-y)2=9,
∴x2-2xy+y2=9.②
由①-②,得4xy=16.∴xy=4.
由①+②,得2x2+2y2=34.
∴x2+y2=17.
五、实践应用
有一张边长为a cm的正方形桌面,因为实际需要,需将正方形边长增加b cm,木工师傅设计了如图所示的三种方案:
小明发现这三种方案都能验证公式:
a2+2ab+b2=(a+b)2,
对于方案一,小明是这样验证的:
a2+ab+ab+b2=a2+2ab+b2=(a+b)2.
请你根据方案二、方案三,写出公式的验证过程.
解:方案二:
a2+ab+b(a+b
=a2+ab+ab+b2
=a2+2ab+b2
=(a+b)2;
方案三:
a2+b(a+a+b)×2
=a2+2ab+b2
=(a+b)2.
提 升 练 习
1、已知x+ =6,则x2+
A.38 B.36 C.34 D.32
2、已知实数a,b满足a+b=2,ab=,则a-b等于( )
A.1 B.- C.±1 D.±
C
C
3、下列运算正确的是( )
A.2x+3y=5x B.5m2·m3=5m5
C.(a-b)2=a2-b2 D.m2·m3=m6
B
C
4、观察等式:2+22=23-2;2+22+23=24-2;2+22+23+24=25-2;……已知按一定规律排列的一组数:250,251,252,…,299,2100.若250=a,用含a的式子表示这组数的和是( )
A.2a2-2a B.2a2-2a-2
C.2a2-a D.2a2+a
解:设y1=2+22+…+2100,y2=2+22+…+2
∴250+251+252+…+299+2100
=y1-y2
=(2+22+…+2100)-(2+22+…+249)
=(2101-2)-(250-2)
=2101-2-250+2
=2101-250
=250(251-1)
=250(2×250-1).
∵250=a,∴原式=a(2a-1)=2a2-a
5、两个正方形的边长之和为5,边长之差为2,那么用较大的正方形的面积减去较小的正方形的面积,差是________.
10
11
解:设两个正方形的边长分别为a,b
∵a+b=5,a-b=2
∴(a+b)(a-b)=a -b =10
∵两个正方形面积差=a -b
∴两个正方形面积差=10
7、4张长为a、宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2.若S1=2S2,则a,b满足什么大小关系?
S1=b(a+b)×2+ab×2+(a-b)2
=a2+2b2,
S2=(a+b)2-S1=(a+b)2-(a2+2b2)
=2ab-b2,
∵S1=2S2,
∴a2+2b2=2(2ab-b2),
整理,得(a-2b)2=0,
∴a-2b=0,
∴a=2b
解:
沪科版数学七年级下
8.3 完全平方公式与平方差公式
第4课时 整式的乘除综合练习
一、整式乘除 法则回顾
同底数幂相乘 am·an=
同底数幂相除 am÷an=
幂的乘方 =
积的乘方 (ab)n=
负整数指数幂 a-p=
am+n
am-n
amn
anbn
1、幂的运算(m,n,p为正整数)
(1)不要忽略指数是“1”的因式.
(2)底数可以是单项式,也可以是多项式,通常把底数看成一个整体来运算.
注 意:
2、整式乘法运算
单项式乘单项式
单项式乘多项式
多项式乘多项式
乘法公式
把系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数 作为积的一个因式
m(a+b)=ma+mb
(m+n)(a+b)
=m(a+b)+n(a+b)
=ma+mb+na+nb
平方差公式: (a+b)(a-b)=a2-b2
完全平方公式: (a±b)2=a2±2ab+b2
3、整式除法运算
单项式除 以单项式
多项式除 以单项式
把系数、同底数幂分别相除,作为商的因式,对于只在被除式中含有的字母,则连同它的指数作为商的一个因式
先把这个多项式的每一项除以这个单项式,再把所得的商相加.
二、整式乘除常见题型例题选讲
1、下列运算正确的是( )
A.(a2)3=a5 B.a2·a4=a8 C.a6÷a3=a2 D.(ab)3=a3b3
2、计算(-a3)2的结果是( )
A.a6 B. -a6 C. -a5 D.a5
3、计算a10÷a2(a≠0)的结果是 ( )
A.a5 B.a-5 C.a8 D.a-8
4、x2·x3=( )
A.x5 B.x6 C.x8 D.x9
一、选择题
D
A
A
幂的运算法则要记忆正确
C
5、小明总结以下结论:①a(b+c)=ab+ac;②a (b+c)=ab-ac;③(b-c)÷a=b÷a-c÷a;④a÷(b+c)=a÷b+a÷c.其中一定成立的个数是( )
A.1 B.2 C.3 D.4
C
6、计算(2x)3÷x的结果正确的是( )
A.8x2 B.6x2 C.8x3 D.6x3
A
7、下列计算正确的是( )
A.a4+a5=a9 B.(2a2b3)2=4a4b6
C.-2a(a+3)=-2a2+6a D.(2a-b)2=4a2-b2
B
混合运算时要注意运算顺序
8、已知4m=a,8n=b,其中m,n为正整数,则22m+6n=( )
A.ab2 B.a+b2 C.a2b3 D.a2+b3
幂的运算法则逆用:
amn=(am)n=(an)m
解:∵4m=a,8n=b
∴22m=a,23n=b
∴22m+6n= 22m×26n= 22m×(23n)2 =ab
A
10、计算(a-2)(a+3)的结果是( )
A.a2-6 B.a2+a-6 C.a2+6 D.a2-a+6
9、化简(x-3)2-x(x-6)的结果为( )
A.6x-9 B.-12x+9 C.9 D.3x+9
解:原式=x2-6x+9-x2+6x=9
C
B
12、下列计算结果为2ab–a2–b2的是( )
A.(a–b)2 B.(–a–b)2
C.–(a+b)2 D.–(a–b)2
11、运用乘法公式计算(a–2)2的结果是( )
A.a2–4a+4 B.a2–2a+4
C.a2–4 D.a2–4a–4
A
D
13、将9.52变形正确的是( )
A.9.52=92+0.52 B.9.52=(10+0.5)(10–0.5)
C.9.52=102–2×10×0.5+0.52 D.9.52=92+9×0.5+0.52
C
14、下列运算中,可用平方差公式计算的是( )
A.(x+y)(x+y) B.(–x+y)(x–y)
C.(–x–y)(y–x) D.(x+y)(–x–y)
C
15、计算(2x+1)(2x–1)等于( )
A.4x2–1 B.2x2–1 C.4x–1 D.4x2+1
A
15
二、填空题
1、若2x=3,2y=5,则2x+y= .
解:2x+y=2x·2y=3×5=15.
2、已知xy=9,x-y=-3,则x +3xy+y =
解:x +3xy+y =x -2xy+y +5xy =(x-y) + 5xy =54
54
3、计算(x-8)(x +8x+64)=
4、计算(4x)M=12x y3-16x3y +4x y ,则 M=
M=(12x y3-16x3y +4x y )÷(4x)=3xy -4x y+xy
3xy -4x y+xy
x3-512
①
②
③
1、下列各题的解法是否正确,如果错了,指出错在什么地方,并改正过来.
×
×
×
漏了单独字母
漏乘1
符号没有变化
三、法则辨析
2、判别下列解法是否正确,若不正确,请说出理由.
解:原式
漏 乘,少了-3x
解:原式
运算法则混淆
四、计算与化简
1、计算:(1)(x 3y)(x+7y); (2)(2x + 5y)(3x 2y).
(3)(3a+b–2)(3a–b+2); (4)(x–y–m+n)(x–y+m–n).
解:
(1) (x 3y)(x+7y)
+
7xy
3yx
=
x2 +4xy–21y2;
21y2
(2) (2x +5 y)(3x 2y)
=
=x2
2x 3x
2x 2y
+5 y 3x
5y 2y
=
6x2
4xy
+ 15xy
10y2
=
6x2 +11xy 10y2.
(4)原式=[(x–y)–(m–n)][(x–y)+(m–n)]
(3)原式=[3a+(b–2)][3a–(b–2)]
=(3a)2–(b–2)2
=9a2–b2+4b–4.
=(x–y)2–(m–n)2
=x2–2xy+y2–m2+2mn–n2.
2、解方程与不等式:
①(x–3)(x–2)+18=(x+9)(x+1);
②(3x+6)(3x–6)<9(x–2)(x+3).
解:①原式去括号,得:x2–5x+6+18=x2+10x+9,
移项合并,得:15x=15,
解得:x=1;
②原式去括号,得:9x2–36<9x2+9x–54,
移项合并,得:9x>18,
解得:x>2 .
化简过程中尽量用乘法公式进行简便运算
3、先化简,再求值:(a+3)2-(a+1)(a-1)-2(2a+4),其中a= - .
解:原式=a2+6a+9-a2+1-4a-8
=2a+2,
当a=-时,
原式=2×(-)+2
=-1+2
=1.
合并同类项不要漏项
方法总结:熟练掌握完全平方公式的变式:
(1)x2+y2
=(x–y)2+2xy
=(x+y)2–2xy,
(2) (x–y)2
=(x+y)2–4xy.
(3)4xy=(x+y)2–(x–y)2
4、已知(x+y)2=25,(x-y)2=9,求xy与x2+y2的值.
解:∵(x+y)2=25,
∴x2+2xy+y2=25.①
∵(x-y)2=9,
∴x2-2xy+y2=9.②
由①-②,得4xy=16.∴xy=4.
由①+②,得2x2+2y2=34.
∴x2+y2=17.
五、实践应用
有一张边长为a cm的正方形桌面,因为实际需要,需将正方形边长增加b cm,木工师傅设计了如图所示的三种方案:
小明发现这三种方案都能验证公式:
a2+2ab+b2=(a+b)2,
对于方案一,小明是这样验证的:
a2+ab+ab+b2=a2+2ab+b2=(a+b)2.
请你根据方案二、方案三,写出公式的验证过程.
解:方案二:
a2+ab+b(a+b
=a2+ab+ab+b2
=a2+2ab+b2
=(a+b)2;
方案三:
a2+b(a+a+b)×2
=a2+2ab+b2
=(a+b)2.
提 升 练 习
1、已知x+ =6,则x2+
A.38 B.36 C.34 D.32
2、已知实数a,b满足a+b=2,ab=,则a-b等于( )
A.1 B.- C.±1 D.±
C
C
3、下列运算正确的是( )
A.2x+3y=5x B.5m2·m3=5m5
C.(a-b)2=a2-b2 D.m2·m3=m6
B
C
4、观察等式:2+22=23-2;2+22+23=24-2;2+22+23+24=25-2;……已知按一定规律排列的一组数:250,251,252,…,299,2100.若250=a,用含a的式子表示这组数的和是( )
A.2a2-2a B.2a2-2a-2
C.2a2-a D.2a2+a
解:设y1=2+22+…+2100,y2=2+22+…+2
∴250+251+252+…+299+2100
=y1-y2
=(2+22+…+2100)-(2+22+…+249)
=(2101-2)-(250-2)
=2101-2-250+2
=2101-250
=250(251-1)
=250(2×250-1).
∵250=a,∴原式=a(2a-1)=2a2-a
5、两个正方形的边长之和为5,边长之差为2,那么用较大的正方形的面积减去较小的正方形的面积,差是________.
10
11
解:设两个正方形的边长分别为a,b
∵a+b=5,a-b=2
∴(a+b)(a-b)=a -b =10
∵两个正方形面积差=a -b
∴两个正方形面积差=10
7、4张长为a、宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2.若S1=2S2,则a,b满足什么大小关系?
S1=b(a+b)×2+ab×2+(a-b)2
=a2+2b2,
S2=(a+b)2-S1=(a+b)2-(a2+2b2)
=2ab-b2,
∵S1=2S2,
∴a2+2b2=2(2ab-b2),
整理,得(a-2b)2=0,
∴a-2b=0,
∴a=2b
解:
