第28章 统计初步 单元测试卷(无答案)沪教版(上海)九年级数学下册
文档属性
| 名称 | 第28章 统计初步 单元测试卷(无答案)沪教版(上海)九年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 166.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 00:00:00 | ||
图片预览


文档简介
第28章 统计初步 单元测试卷
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )
1. 希望中学制作了学生选择棋类,武术,摄影,刺绣四门校本课程情况的扇形统计图,从图中可以看出选择刺绣的学生为( )
A. B. C. D.
2. 在《科学》课上,老师讲到温度计的使用方法及液体的沸点时,好奇的王红同学准备测量食用油的沸点,已知食用油的沸点温度高于水的沸点温度,王红家只有刻度不超过的温度计,她的方法是在锅中倒入一些食用油,用煤气灶均匀加热,并每隔测量一次锅中油温,测量得到的数据如下表:
时间
油温
王红发现,烧了时,油沸腾了,则下列说法不正确的是
A.没有加热时,油的温度是
B.加热,油的温度是
C.估计这种食用油的沸点温度约是
D.每加热,油的温度升高
3. 一组数据共个,分为组,第组的频数分别为,,,,第组的频率为,则第组的频数为( )
A. B. C. D.
4. 张大娘为了提高家庭收入,买来头小猪.经过精心饲养,不到个月就可以出售了,下表为这些猪出售时的体重:
体重
频数
则这些猪体重的平均数和中位数分别是( )
A., B., C., D.,
5. 如图是甲、乙两射击运动员的次射击训练成绩的折线统计图,则下列说法正确的是( )
A.甲比乙的成绩稳定 B.乙比甲的成绩稳定
C.甲、乙两人的成绩一样稳定 D.无法确定谁的成绩更稳定
6. 既可以表示数量的多少,又能清楚地表示出数量增减变化的统计图是( )
A.条形统计图 B.折线统计图 C.扇形统计图 D.复式统计图
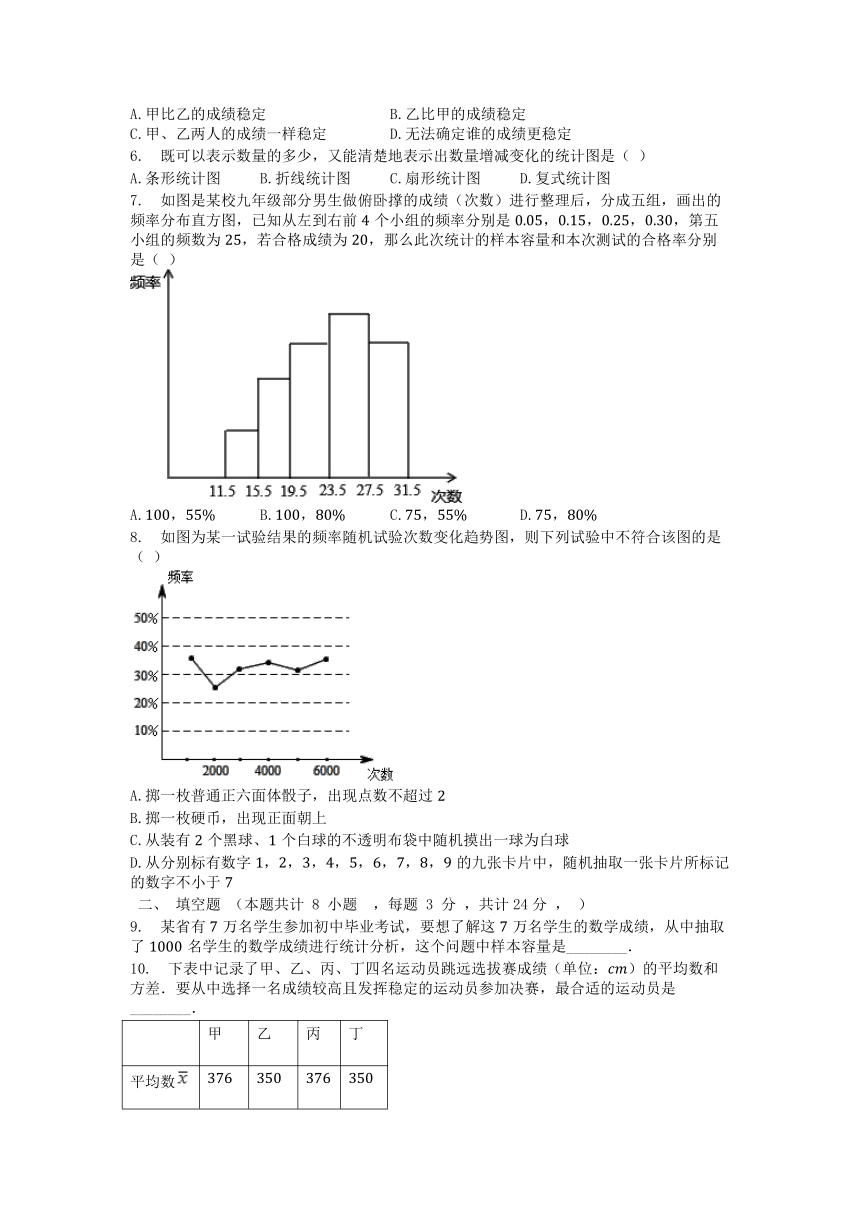
7. 如图是某校九年级部分男生做俯卧撑的成绩(次数)进行整理后,分成五组,画出的频率分布直方图,已知从左到右前个小组的频率分别是,,,,第五小组的频数为,若合格成绩为,那么此次统计的样本容量和本次测试的合格率分别是( )
A., B., C., D.,
8. 如图为某一试验结果的频率随机试验次数变化趋势图,则下列试验中不符合该图的是( )
A.掷一枚普通正六面体骰子,出现点数不超过
B.掷一枚硬币,出现正面朝上
C.从装有个黑球、个白球的不透明布袋中随机摸出一球为白球
D.从分别标有数字,,,,,,,,的九张卡片中,随机抽取一张卡片所标记的数字不小于
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )
9. 某省有万名学生参加初中毕业考试,要想了解这万名学生的数学成绩,从中抽取了名学生的数学成绩进行统计分析,这个问题中样本容量是________.
10. 下表中记录了甲、乙、丙、丁四名运动员跳远选拔赛成绩(单位:)的平均数和方差.要从中选择一名成绩较高且发挥稳定的运动员参加决赛,最合适的运动员是________.
甲
乙
丙
丁
平均数
方差
11. 某出租车公司在“五 一”长假期间平均每天的营业额为万元,由此推断月份的总营业额约为(万元).根据所学的统计知识,你认为这样的推断是否合理?答:________.
12. 若某扇形的圆心角为,则该扇形所表示的部分占总体的百分比为________.
13. 如下表是七年级某班名同学数学测试成绩,根据信息完成下列问题:
①完成表中的空格信息;
②人中最高分是谁?最低分是谁?分数与全班平均分最接近的是谁?
姓名 王芳 刘兵 张昕 李聪 江文
成绩 ________ ________ ________
与全班平
均分之差 ________
14. 如果一组数据:,,,,的平均数是,则等于________.
15. 两组数据:,,,与,,的平均数都是.若将这两组数据合并为一组新数据,则这组新数据的众数为________.
16. 小明在体考时选择了投掷实心球,如图是体育老师记录的小明在训练时投掷实心球的次成绩的折线统计图.这次成绩的中位数是________.
三、 解答题 (本题共计 8 小题 ,共计72分 , )
17. 生物专家们想了解一下某种鸟类在该区的数量,首先他们捕捉了只鸟,作上标记,放回大自然,过了几天,他们又随意捕捉了只,发现有只带标记的鸟,你能估计一下该地区有多少只鸟吗?
18. 已知甲校有人,女生占;乙校有人,女生占.甲、乙两校合并后,小明认为:
“因为,所以合并后的女生占总人数的.”老师认为小明的想法是错误的.
(1)如果是你,你会怎么列式计算合并后女生在总人数中所占的百分比?
(2)请指出在什么情况下小明的答案是正确的,并通过计算说明.
19. 为了解学生每天回家完成作业时间的情况,某中学对学生每天回家完成作业的时间进行抽样调查,并将调查结果绘制成如下两幅不完整的统计图,请回答下列问题.
被抽样调查的学生有________人,补全条形统计图;
每天回家完成作业的时间的中位数是________小时,众数是________小时;
若该校共有名学生,请估计该校每天回家完成作业的时间超过小时的学生有多少人?
20. 为了考察甲、乙两种小麦的长势,分别从中抽出株苗,测得苗高如下(单位:):
甲
乙
(1)计算甲、乙两种小麦苗高的平均数;
(2)计算甲、乙两种小麦苗高的方差,并判断哪种小麦长得比较整齐?
21. “数学是宇宙中最美的语言.”为进一步提升大家的数学成绩,郑州某区随机抽取了名学生的期末数学成绩(成绩为百分制),希望通过数据展示大家的实力,并根据成绩来制定相应的提升措施,经过整理数据得到以下信息:
信息:名学生数学成绩频数分布直方图如图所示,从左到右依次为第一组到第五组(每组数据含前端点值,不含后端点值).
信息:第三组的成绩(单位:分)为 .
根据信息解答下列问题:
补全第二组频数分布直方图(直接在图中补全);
第三组成绩的众数是________分,抽取的名学生成绩的中位数是________分;
若该区共有名学生考试,请估计该区学生成绩不低于分的人数.
22. 为了考察某班普通话测试情况,从中抽查了人的成绩如下(单位:分):
,,,,,,,,,.
(1)这个问题中,总体、个体、样本各是什么?
(2)这个问题中,样本平均数、方差、标准差各是多少并估计总体平均数、方差、标准差?(平均数精确到分,标准差保留三个有效数字).
23. 嘉嘉和淇淇是九班运动素质最好的两位同学,为了选出一名同学参加全校的体育运动大赛,班主任针对学校要测试的五个项目,对两位同学进行相应的测试(成绩:分),结果如下:
姓名 力量 速度 耐力 柔韧 灵敏
嘉嘉
淇淇
根据以上测试结果解答下列问题.
补充完成下表:
姓名 平均成绩(分) 中位数(分) 众数(分) 方差(分)
嘉嘉
淇淇
从平均数和方差角度分析推选哪位同学参加学校的比赛比较合适?并说明理由.
若按力量:速度:耐力:柔韧:灵敏的比例折合成综合分数,推选得分高的同学参加比赛,请通过计算说明应推选哪位同学去参赛.
24. 某教育局组织了“落实十九大精神,立足岗位见行动”教师演讲比赛,根据各校初赛成绩在小学组、中学组分别选出名教师参加决赛,这些选手的决赛成绩如图所示:
根据上图提供的信息,回答下列问题:
(1)请你把下面表格填写完整:
团体成绩 众数 平均数 方差
小学组 ________
中学组 ________
(2)考虑平均数与方差,你认为哪个组的团体成绩更好些,并说明理由;
(3)若在每组的决赛选手中分别选出人参加总决赛,你认为哪个组获胜的可能性大些?请说明理由.
试卷第1页,总1页
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )
1. 希望中学制作了学生选择棋类,武术,摄影,刺绣四门校本课程情况的扇形统计图,从图中可以看出选择刺绣的学生为( )
A. B. C. D.
2. 在《科学》课上,老师讲到温度计的使用方法及液体的沸点时,好奇的王红同学准备测量食用油的沸点,已知食用油的沸点温度高于水的沸点温度,王红家只有刻度不超过的温度计,她的方法是在锅中倒入一些食用油,用煤气灶均匀加热,并每隔测量一次锅中油温,测量得到的数据如下表:
时间
油温
王红发现,烧了时,油沸腾了,则下列说法不正确的是
A.没有加热时,油的温度是
B.加热,油的温度是
C.估计这种食用油的沸点温度约是
D.每加热,油的温度升高
3. 一组数据共个,分为组,第组的频数分别为,,,,第组的频率为,则第组的频数为( )
A. B. C. D.
4. 张大娘为了提高家庭收入,买来头小猪.经过精心饲养,不到个月就可以出售了,下表为这些猪出售时的体重:
体重
频数
则这些猪体重的平均数和中位数分别是( )
A., B., C., D.,
5. 如图是甲、乙两射击运动员的次射击训练成绩的折线统计图,则下列说法正确的是( )
A.甲比乙的成绩稳定 B.乙比甲的成绩稳定
C.甲、乙两人的成绩一样稳定 D.无法确定谁的成绩更稳定
6. 既可以表示数量的多少,又能清楚地表示出数量增减变化的统计图是( )
A.条形统计图 B.折线统计图 C.扇形统计图 D.复式统计图
7. 如图是某校九年级部分男生做俯卧撑的成绩(次数)进行整理后,分成五组,画出的频率分布直方图,已知从左到右前个小组的频率分别是,,,,第五小组的频数为,若合格成绩为,那么此次统计的样本容量和本次测试的合格率分别是( )
A., B., C., D.,
8. 如图为某一试验结果的频率随机试验次数变化趋势图,则下列试验中不符合该图的是( )
A.掷一枚普通正六面体骰子,出现点数不超过
B.掷一枚硬币,出现正面朝上
C.从装有个黑球、个白球的不透明布袋中随机摸出一球为白球
D.从分别标有数字,,,,,,,,的九张卡片中,随机抽取一张卡片所标记的数字不小于
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )
9. 某省有万名学生参加初中毕业考试,要想了解这万名学生的数学成绩,从中抽取了名学生的数学成绩进行统计分析,这个问题中样本容量是________.
10. 下表中记录了甲、乙、丙、丁四名运动员跳远选拔赛成绩(单位:)的平均数和方差.要从中选择一名成绩较高且发挥稳定的运动员参加决赛,最合适的运动员是________.
甲
乙
丙
丁
平均数
方差
11. 某出租车公司在“五 一”长假期间平均每天的营业额为万元,由此推断月份的总营业额约为(万元).根据所学的统计知识,你认为这样的推断是否合理?答:________.
12. 若某扇形的圆心角为,则该扇形所表示的部分占总体的百分比为________.
13. 如下表是七年级某班名同学数学测试成绩,根据信息完成下列问题:
①完成表中的空格信息;
②人中最高分是谁?最低分是谁?分数与全班平均分最接近的是谁?
姓名 王芳 刘兵 张昕 李聪 江文
成绩 ________ ________ ________
与全班平
均分之差 ________
14. 如果一组数据:,,,,的平均数是,则等于________.
15. 两组数据:,,,与,,的平均数都是.若将这两组数据合并为一组新数据,则这组新数据的众数为________.
16. 小明在体考时选择了投掷实心球,如图是体育老师记录的小明在训练时投掷实心球的次成绩的折线统计图.这次成绩的中位数是________.
三、 解答题 (本题共计 8 小题 ,共计72分 , )
17. 生物专家们想了解一下某种鸟类在该区的数量,首先他们捕捉了只鸟,作上标记,放回大自然,过了几天,他们又随意捕捉了只,发现有只带标记的鸟,你能估计一下该地区有多少只鸟吗?
18. 已知甲校有人,女生占;乙校有人,女生占.甲、乙两校合并后,小明认为:
“因为,所以合并后的女生占总人数的.”老师认为小明的想法是错误的.
(1)如果是你,你会怎么列式计算合并后女生在总人数中所占的百分比?
(2)请指出在什么情况下小明的答案是正确的,并通过计算说明.
19. 为了解学生每天回家完成作业时间的情况,某中学对学生每天回家完成作业的时间进行抽样调查,并将调查结果绘制成如下两幅不完整的统计图,请回答下列问题.
被抽样调查的学生有________人,补全条形统计图;
每天回家完成作业的时间的中位数是________小时,众数是________小时;
若该校共有名学生,请估计该校每天回家完成作业的时间超过小时的学生有多少人?
20. 为了考察甲、乙两种小麦的长势,分别从中抽出株苗,测得苗高如下(单位:):
甲
乙
(1)计算甲、乙两种小麦苗高的平均数;
(2)计算甲、乙两种小麦苗高的方差,并判断哪种小麦长得比较整齐?
21. “数学是宇宙中最美的语言.”为进一步提升大家的数学成绩,郑州某区随机抽取了名学生的期末数学成绩(成绩为百分制),希望通过数据展示大家的实力,并根据成绩来制定相应的提升措施,经过整理数据得到以下信息:
信息:名学生数学成绩频数分布直方图如图所示,从左到右依次为第一组到第五组(每组数据含前端点值,不含后端点值).
信息:第三组的成绩(单位:分)为 .
根据信息解答下列问题:
补全第二组频数分布直方图(直接在图中补全);
第三组成绩的众数是________分,抽取的名学生成绩的中位数是________分;
若该区共有名学生考试,请估计该区学生成绩不低于分的人数.
22. 为了考察某班普通话测试情况,从中抽查了人的成绩如下(单位:分):
,,,,,,,,,.
(1)这个问题中,总体、个体、样本各是什么?
(2)这个问题中,样本平均数、方差、标准差各是多少并估计总体平均数、方差、标准差?(平均数精确到分,标准差保留三个有效数字).
23. 嘉嘉和淇淇是九班运动素质最好的两位同学,为了选出一名同学参加全校的体育运动大赛,班主任针对学校要测试的五个项目,对两位同学进行相应的测试(成绩:分),结果如下:
姓名 力量 速度 耐力 柔韧 灵敏
嘉嘉
淇淇
根据以上测试结果解答下列问题.
补充完成下表:
姓名 平均成绩(分) 中位数(分) 众数(分) 方差(分)
嘉嘉
淇淇
从平均数和方差角度分析推选哪位同学参加学校的比赛比较合适?并说明理由.
若按力量:速度:耐力:柔韧:灵敏的比例折合成综合分数,推选得分高的同学参加比赛,请通过计算说明应推选哪位同学去参赛.
24. 某教育局组织了“落实十九大精神,立足岗位见行动”教师演讲比赛,根据各校初赛成绩在小学组、中学组分别选出名教师参加决赛,这些选手的决赛成绩如图所示:
根据上图提供的信息,回答下列问题:
(1)请你把下面表格填写完整:
团体成绩 众数 平均数 方差
小学组 ________
中学组 ________
(2)考虑平均数与方差,你认为哪个组的团体成绩更好些,并说明理由;
(3)若在每组的决赛选手中分别选出人参加总决赛,你认为哪个组获胜的可能性大些?请说明理由.
试卷第1页,总1页
