沪教版上海中考专题复习《统计初步》综合练习(PDF版,无答案)
文档属性
| 名称 | 沪教版上海中考专题复习《统计初步》综合练习(PDF版,无答案) | 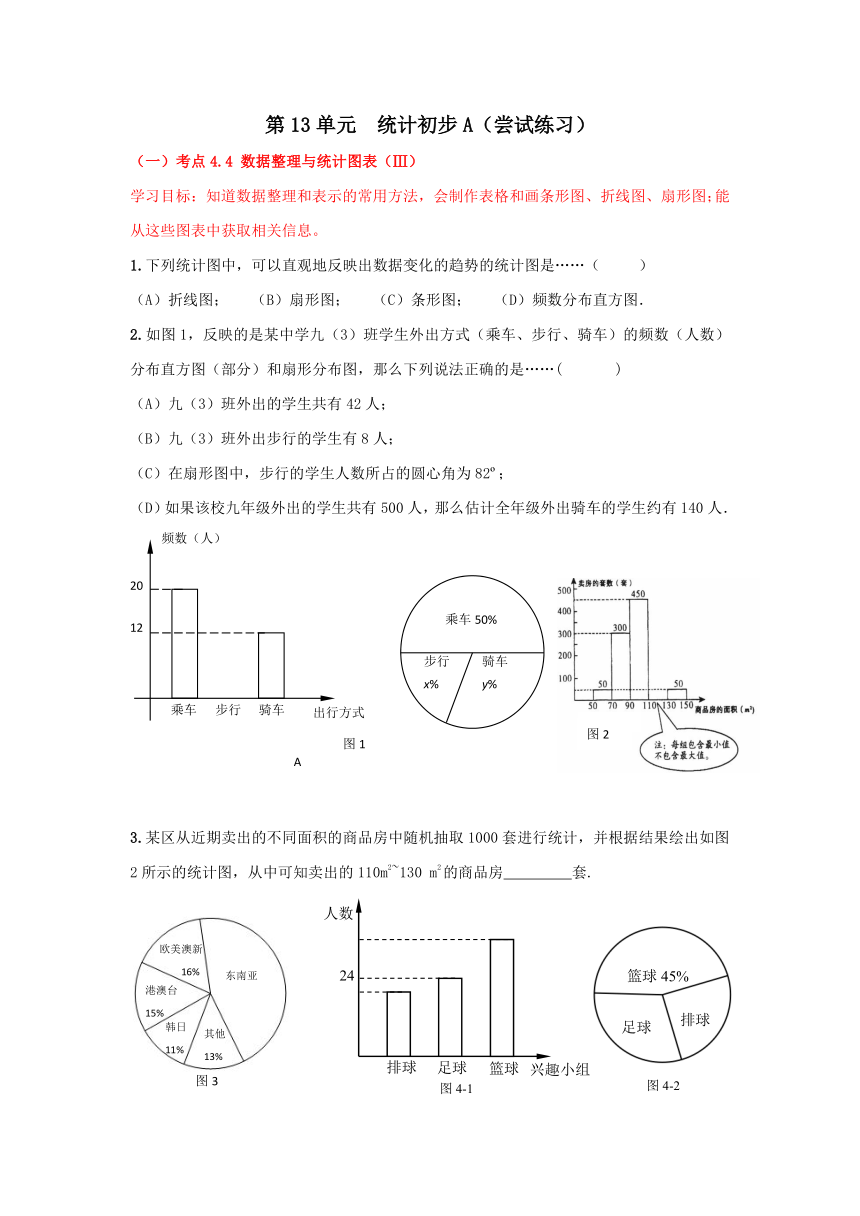 | |
| 格式 | |||
| 文件大小 | 203.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 09:16:31 | ||
图片预览


文档简介
第 13 单元 统计初步 A(尝试练习)
(一)考点 4.4 数据整理与统计图表(Ⅲ)
学习目标:知道数据整理和表示的常用方法,会制作表格和画条形图、折线图、扇形图;能
从这些图表中获取相关信息。
1.下列统计图中,可以直观地反映出数据变化的趋势的统计图是……( )
(A)折线图; (B)扇形图; (C)条形图; (D)频数分布直方图.
2.如图 1,反映的是某中学九(3)班学生外出方式(乘车、步行、骑车)的频数(人数)
分布直方图(部分)和扇形分布图,那么下列说法正确的是……( )
(A)九(3)班外出的学生共有 42 人;
(B)九(3)班外出步行的学生有 8人;
(C)在扇形图中,步行的学生人数所占的圆心角为 82 ;
(D)如果该校九年级外出的学生共有 500 人,那么估计全年级外出骑车的学生约有 140 人.
频数(人)
20
12 乘车 50%
步行 骑车
x% y%
乘车 步行 骑车 出行方式
图 2
图 1
A
3.某区从近期卖出的不同面积的商品房中随机抽取 1000 套进行统计,并根据结果绘出如图
2 2
2 所示的统计图,从中可知卖出的 110m ~130 m 的商品房 套.
人数
欧美澳新
16% 东南亚 24 篮球 45%
港澳台
15%
排球
韩日
其他 足球
11% 13%
排球 足球 篮球 兴趣小组
图 3
图 4-1 图 4-2
4.2018 年春节期间,反季游成为出境游的热门,中国游客青睐的目的地仍主要集中在温暖
的东南亚地区.据调查发现 2018 年春节期间出境游约有 700 万人,游客目的地分布情况的
扇形图如图 3所示,从中可知出境游东南亚地区的游客约有 万人.
5.张老师对本校参加体育兴趣小组的情况进行调查,图 4-1 和图 4-2 是收集数据后绘制的两
幅不完整统计图.已知参加体育兴趣小组的学生共有 80 名,其中每名学生只参加一个兴趣
小组.根据图中提供的信息,可知参加排球兴趣小组的人数占参加体育兴趣小组总人数的百
分数是 .
(二)考点 4.5 统计的意义 (Ⅰ)
学习目标:知道统计的意义,理解统计中的总体、个体、样本、普查、抽样调查、随机样本
等有关概念;知道用随机样本推断总体是重要的统计思想,并初步体会这一统计思想的运用。
1.为了了解某校九年级 400 名学生的体重情况,从中抽取 50 名学生的体重进行分析.在这项
调查中,样本是指……( )
(A)400 名学生; (B)被抽取的 50 名学生;
(C)400 名学生的体重; (D)被抽取的 50 名学生的体重.
2.学校环保小组的同学随机调查了某小区 10 户家庭一周内使用环保方便袋的数量,数据如
下(单位:只):6,5,7,8,7,5,7,10,6,9.利用学过的统计知识,根据上述数据估
计该小区 200 户家庭一周内共需要环保方便袋约……( )
(A)200 只; (B)1400 只; (C)9800 只; (D)14000 只.
3.在开展“国学诵读”活动中,某校为了解全
校 1200 名学生课外阅读的情况,随机调查了 50
名学生一周的课外阅读时间,并绘制成如图 4
所示的条形统计图.根据图中数据,估计该校
1200 名学生一周的课外阅读时间不少于 6小时
的人数是 . 图 4
(三)考点 4.6 平均数、加权平均数、中位数、众数的概念和计算 (Ⅲ)
学习目标:理解平均数、加权平均数、中位数和众数等概念,会求一组数据的平均数或加权
平均数;会确定一组数据的中位数和众数;能根据实际问题,在平均数、中位数和众数种选
择合适的量来表示一组数据的平均水平。
1.某居民小区开展节约用水活动,3月份各户用水量比 2月份有所下降,不同节水量的户
数统计如下表所示,那么 3月份平均每户节水量是……( )
节水量(立方米) 1 2 3
户数 20 120 60
(A)1.9 立方米;(B)2.2 立方米: (C)33.33 立方米; (D)66.67 立方米.
2.在一次引体向上的测试中,小强等 5 位同学引体向上的次数分别为: 6, 8, 9, 8, 9,那么
关于这组数据的说法正确的是 ……( )
(A)平均数是 8.5; (B)中位数是 8.5; (C)众数是 8.5; (D)众数是 8和 9.
3.如果一组数据 3、4、5、6、 x、8的众数是 4,那么这组数据的中位数是……( )
(A)4; (B)4.5; (C)5; (D)5.5.
4.一个民营企业 10 名员工的月平均工资如下表,则能较好反映这些员工月平均工资水平的
是……( ) (工资单位:万元)
人次 1 1 1 2 1 1 3
工资 30 3 2 1.5 1.2 1 0.8
(A)平均数; (B)中位数; (C)众数; (D)标准差.
5.下表是某班所有学生体育中考模拟测试成绩的统计表,表格中的每个分数段含最小值,不
含最大值,根据表中数据可以知道,该班这次体育中考模拟测试成绩的中位数落在的分
数段是 .
分数段 18分以下 18 22分 22 26分 26 30分 30分
人数 3 7 9 13 8
(四)考点 4.7 方差、标准差的概念和计算 (Ⅲ)
学习目标:理解方差、标准差的概念,会计算一组数据的方差和标准差;能根据一组数据的
方差或标准差来解释数据的波动性。
1.下列各统计量中,表示一组数据离散程度的量是……( )
(A)平均数; (B)众数: (C)方差; (D)频数.
2.某运动员进行射击测试,共射靶 6次,成绩记录如下:8.5,9.0,10,8.0,9.5,10,
在下列各统计量中,表示这组数据离散程度的量是……( )
(A)平均数; (B) 众数; (C) 方差; (D) 频率.
3.数据 0,1,1,3,3,4 的平均数和方差分别是 ……( )
(A)2 和 1.6; (B)2和 2; (C)2.4 和 1.6 ; (D)2.4 和 2.
4.数据1、 2、3、3、6的方差是 .
(五)考点 4.8 频数、频率的意义和计算,画频数分布直方图和频率分布直方图 (Ⅱ)
学习目标:理解组频率的概念;对一组数据,在给定分组的情况下会制作频数分布表、频率
分布表,会绘制频率数分布直方图和频率分布直方图;能从频数分布直方图和频率分布直方
图中获取有关信息以及判断数据分布情况。
1.已知一个 40 个数据的样本,把它分成 6组,第一组到第四组的频数分别是 10、5、7、6,
第五组的频率是 0.1,那么第六组的频数是 .
2.某校随机抽查若干名学生,测试了 1分钟仰卧起 人数
12
坐的次数,把所得数据绘制成频数分布直方图(如 10
图),则仰卧起坐次数不小于 15 次且小于 20 次的频 5
3
率是……( ) 0 15 20 25 30 35 次数
A. 0.1; B. 0.2; C. 0.3; D. 0.4. 注:每组可含最小值,不含最大值
3.将某班女生的身高分成三组,情况如右表所示,
第一组 第二组 第三组
则表中 a的值是……( ) 频数 6 10 a
(A)2; (B)4; 频率 b c 20%
(C)6; (D)8. 分 数 段 频数 频率
4. 秋季新学期开学时,某中学对六年级新生掌握“中 60≤x<70 6 a
学生日常行为规范”的情况进行了知识测试,测试成绩 70≤x<80 20 0.4
全部合格,现学校随机选取了部分学生的成绩,整理并 80≤x<90 15 b
制作成了不完整的图表(如表 1 所示),图表中 90≤x≤100 c 0.18
c .
5.通常在频率分布直方图中,用每小组对应的小矩形的面积表示该小组的组频率. 因此,
频率分布直方图的纵轴表示……( )
频数 频率 频率 频数
(A)组距; (B)组距; (C)组数; (D)组数.
(六)考点 4.9 中位数、众数、方差、标准差、频数、频率的简单应用 (Ⅲ)
学习目标:具有初步的统计意识,能运用所学的统计知识解决现实生活中的简单的统计问题。
1.在学校举办的“中华诗词大赛”中,有 11 名选手进入决赛,他们的决赛成绩各不相同,
其中一名参赛选手想知道自己是否能进入前6名,他需要了解这11名学生成绩的……( )
(A)中位数; (B)平均数; (C)众数; (D)方差.
2.已知两组数据:a1,a2,a3,a4,a5和 a1-1,a2-1,a3-1,a4-1,a5-1,
下列判断中错误的是……( )
(A) 平均数不相等,方差相等; (B) 中位数不相等,标准差相等;
(C) 平均数相等,标准差不相等; (D) 中位数不相等,方差相等.
3. 下列说法正确的是( )
(A)一组数据的中位数一定等于该组数据中的某个数据;
(B)一组数据的平均数和中位数一定不相等;
(C)一组数据的众数可以有几个;
(D)一组数据的方差一定大于这组数据的标准差.
4.甲、乙、丙、丁四位同学五次数学测验成绩统
甲 乙 丙 丁
计如下表.如果从这四位同学中选出一位成绩较
平均分 70 85 85 70
好且状态稳定的同学参加初中数学竞赛,那么应
标准差 6.5 6.5 7.6 7.6
选 同学.
5.为了解某山区金丝猴的数量,科研人员在该山区不同的地方捕获了 15 只金丝猴,并在它
们的身上做上标记后放回该山区.过段时间后,在该山区不同的地方又捕获了 32 只金丝猴,
其中 4只身上有上次做的标记,由此可以估计该山区金丝猴的数量约有 只.
(一)考点 4.4 数据整理与统计图表(Ⅲ)
学习目标:知道数据整理和表示的常用方法,会制作表格和画条形图、折线图、扇形图;能
从这些图表中获取相关信息。
1.下列统计图中,可以直观地反映出数据变化的趋势的统计图是……( )
(A)折线图; (B)扇形图; (C)条形图; (D)频数分布直方图.
2.如图 1,反映的是某中学九(3)班学生外出方式(乘车、步行、骑车)的频数(人数)
分布直方图(部分)和扇形分布图,那么下列说法正确的是……( )
(A)九(3)班外出的学生共有 42 人;
(B)九(3)班外出步行的学生有 8人;
(C)在扇形图中,步行的学生人数所占的圆心角为 82 ;
(D)如果该校九年级外出的学生共有 500 人,那么估计全年级外出骑车的学生约有 140 人.
频数(人)
20
12 乘车 50%
步行 骑车
x% y%
乘车 步行 骑车 出行方式
图 2
图 1
A
3.某区从近期卖出的不同面积的商品房中随机抽取 1000 套进行统计,并根据结果绘出如图
2 2
2 所示的统计图,从中可知卖出的 110m ~130 m 的商品房 套.
人数
欧美澳新
16% 东南亚 24 篮球 45%
港澳台
15%
排球
韩日
其他 足球
11% 13%
排球 足球 篮球 兴趣小组
图 3
图 4-1 图 4-2
4.2018 年春节期间,反季游成为出境游的热门,中国游客青睐的目的地仍主要集中在温暖
的东南亚地区.据调查发现 2018 年春节期间出境游约有 700 万人,游客目的地分布情况的
扇形图如图 3所示,从中可知出境游东南亚地区的游客约有 万人.
5.张老师对本校参加体育兴趣小组的情况进行调查,图 4-1 和图 4-2 是收集数据后绘制的两
幅不完整统计图.已知参加体育兴趣小组的学生共有 80 名,其中每名学生只参加一个兴趣
小组.根据图中提供的信息,可知参加排球兴趣小组的人数占参加体育兴趣小组总人数的百
分数是 .
(二)考点 4.5 统计的意义 (Ⅰ)
学习目标:知道统计的意义,理解统计中的总体、个体、样本、普查、抽样调查、随机样本
等有关概念;知道用随机样本推断总体是重要的统计思想,并初步体会这一统计思想的运用。
1.为了了解某校九年级 400 名学生的体重情况,从中抽取 50 名学生的体重进行分析.在这项
调查中,样本是指……( )
(A)400 名学生; (B)被抽取的 50 名学生;
(C)400 名学生的体重; (D)被抽取的 50 名学生的体重.
2.学校环保小组的同学随机调查了某小区 10 户家庭一周内使用环保方便袋的数量,数据如
下(单位:只):6,5,7,8,7,5,7,10,6,9.利用学过的统计知识,根据上述数据估
计该小区 200 户家庭一周内共需要环保方便袋约……( )
(A)200 只; (B)1400 只; (C)9800 只; (D)14000 只.
3.在开展“国学诵读”活动中,某校为了解全
校 1200 名学生课外阅读的情况,随机调查了 50
名学生一周的课外阅读时间,并绘制成如图 4
所示的条形统计图.根据图中数据,估计该校
1200 名学生一周的课外阅读时间不少于 6小时
的人数是 . 图 4
(三)考点 4.6 平均数、加权平均数、中位数、众数的概念和计算 (Ⅲ)
学习目标:理解平均数、加权平均数、中位数和众数等概念,会求一组数据的平均数或加权
平均数;会确定一组数据的中位数和众数;能根据实际问题,在平均数、中位数和众数种选
择合适的量来表示一组数据的平均水平。
1.某居民小区开展节约用水活动,3月份各户用水量比 2月份有所下降,不同节水量的户
数统计如下表所示,那么 3月份平均每户节水量是……( )
节水量(立方米) 1 2 3
户数 20 120 60
(A)1.9 立方米;(B)2.2 立方米: (C)33.33 立方米; (D)66.67 立方米.
2.在一次引体向上的测试中,小强等 5 位同学引体向上的次数分别为: 6, 8, 9, 8, 9,那么
关于这组数据的说法正确的是 ……( )
(A)平均数是 8.5; (B)中位数是 8.5; (C)众数是 8.5; (D)众数是 8和 9.
3.如果一组数据 3、4、5、6、 x、8的众数是 4,那么这组数据的中位数是……( )
(A)4; (B)4.5; (C)5; (D)5.5.
4.一个民营企业 10 名员工的月平均工资如下表,则能较好反映这些员工月平均工资水平的
是……( ) (工资单位:万元)
人次 1 1 1 2 1 1 3
工资 30 3 2 1.5 1.2 1 0.8
(A)平均数; (B)中位数; (C)众数; (D)标准差.
5.下表是某班所有学生体育中考模拟测试成绩的统计表,表格中的每个分数段含最小值,不
含最大值,根据表中数据可以知道,该班这次体育中考模拟测试成绩的中位数落在的分
数段是 .
分数段 18分以下 18 22分 22 26分 26 30分 30分
人数 3 7 9 13 8
(四)考点 4.7 方差、标准差的概念和计算 (Ⅲ)
学习目标:理解方差、标准差的概念,会计算一组数据的方差和标准差;能根据一组数据的
方差或标准差来解释数据的波动性。
1.下列各统计量中,表示一组数据离散程度的量是……( )
(A)平均数; (B)众数: (C)方差; (D)频数.
2.某运动员进行射击测试,共射靶 6次,成绩记录如下:8.5,9.0,10,8.0,9.5,10,
在下列各统计量中,表示这组数据离散程度的量是……( )
(A)平均数; (B) 众数; (C) 方差; (D) 频率.
3.数据 0,1,1,3,3,4 的平均数和方差分别是 ……( )
(A)2 和 1.6; (B)2和 2; (C)2.4 和 1.6 ; (D)2.4 和 2.
4.数据1、 2、3、3、6的方差是 .
(五)考点 4.8 频数、频率的意义和计算,画频数分布直方图和频率分布直方图 (Ⅱ)
学习目标:理解组频率的概念;对一组数据,在给定分组的情况下会制作频数分布表、频率
分布表,会绘制频率数分布直方图和频率分布直方图;能从频数分布直方图和频率分布直方
图中获取有关信息以及判断数据分布情况。
1.已知一个 40 个数据的样本,把它分成 6组,第一组到第四组的频数分别是 10、5、7、6,
第五组的频率是 0.1,那么第六组的频数是 .
2.某校随机抽查若干名学生,测试了 1分钟仰卧起 人数
12
坐的次数,把所得数据绘制成频数分布直方图(如 10
图),则仰卧起坐次数不小于 15 次且小于 20 次的频 5
3
率是……( ) 0 15 20 25 30 35 次数
A. 0.1; B. 0.2; C. 0.3; D. 0.4. 注:每组可含最小值,不含最大值
3.将某班女生的身高分成三组,情况如右表所示,
第一组 第二组 第三组
则表中 a的值是……( ) 频数 6 10 a
(A)2; (B)4; 频率 b c 20%
(C)6; (D)8. 分 数 段 频数 频率
4. 秋季新学期开学时,某中学对六年级新生掌握“中 60≤x<70 6 a
学生日常行为规范”的情况进行了知识测试,测试成绩 70≤x<80 20 0.4
全部合格,现学校随机选取了部分学生的成绩,整理并 80≤x<90 15 b
制作成了不完整的图表(如表 1 所示),图表中 90≤x≤100 c 0.18
c .
5.通常在频率分布直方图中,用每小组对应的小矩形的面积表示该小组的组频率. 因此,
频率分布直方图的纵轴表示……( )
频数 频率 频率 频数
(A)组距; (B)组距; (C)组数; (D)组数.
(六)考点 4.9 中位数、众数、方差、标准差、频数、频率的简单应用 (Ⅲ)
学习目标:具有初步的统计意识,能运用所学的统计知识解决现实生活中的简单的统计问题。
1.在学校举办的“中华诗词大赛”中,有 11 名选手进入决赛,他们的决赛成绩各不相同,
其中一名参赛选手想知道自己是否能进入前6名,他需要了解这11名学生成绩的……( )
(A)中位数; (B)平均数; (C)众数; (D)方差.
2.已知两组数据:a1,a2,a3,a4,a5和 a1-1,a2-1,a3-1,a4-1,a5-1,
下列判断中错误的是……( )
(A) 平均数不相等,方差相等; (B) 中位数不相等,标准差相等;
(C) 平均数相等,标准差不相等; (D) 中位数不相等,方差相等.
3. 下列说法正确的是( )
(A)一组数据的中位数一定等于该组数据中的某个数据;
(B)一组数据的平均数和中位数一定不相等;
(C)一组数据的众数可以有几个;
(D)一组数据的方差一定大于这组数据的标准差.
4.甲、乙、丙、丁四位同学五次数学测验成绩统
甲 乙 丙 丁
计如下表.如果从这四位同学中选出一位成绩较
平均分 70 85 85 70
好且状态稳定的同学参加初中数学竞赛,那么应
标准差 6.5 6.5 7.6 7.6
选 同学.
5.为了解某山区金丝猴的数量,科研人员在该山区不同的地方捕获了 15 只金丝猴,并在它
们的身上做上标记后放回该山区.过段时间后,在该山区不同的地方又捕获了 32 只金丝猴,
其中 4只身上有上次做的标记,由此可以估计该山区金丝猴的数量约有 只.
