2021—2022学年人教版数学八年级下册20.2数据的波动程度 巩固练习(word版、含答案)
文档属性
| 名称 | 2021—2022学年人教版数学八年级下册20.2数据的波动程度 巩固练习(word版、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 230.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 20:49:57 | ||
图片预览


文档简介
2021-2022学年八年级下册数学巩固练习(人教版)
20.2 数据的波动程度
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某校举行健美操比赛,甲、乙两个班选20名学生参加比赛,两个班参赛学生的平均身高都是1.65米,其方差分别是,,则参赛学生身高比较整齐的班级是( )
A.甲班 B.乙班 C.同样整齐 D.无法确定
2.对于一组统计数据3,3,6,5,3下列说法正确的是( )
A.中位数是6 B.平均数是5 C.方差是1.7 D.众数是3
3.下图是甲、乙两同学五次数学测试成绩的折线图.比较甲、乙的成绩,下列说法正确的是( )
A.甲平均分高,成绩稳定 B.甲平均分高,成绩不稳定
C.乙平均分高,成绩稳定 D.乙平均分高,成绩不稳定
4.已知一组数据的方差,则的值为( )
A.22 B.21 C.20 D.7
5.在庆祝中国共产党成立100周年的“红色记忆”校园歌咏比赛中,15个参赛班级按照成绩(成绩各不相同)取前7名进入决赛,小红知道了自己班级的比赛成绩,如果要判断自己的班级能否进入决赛,还需要知道这15个参赛班级成绩的( )
A.平均数 B.中位数 C.众数 D.方差
6.为调动学生参与体育锻炼的积极性,某校组织了一分钟跳绳比赛活动,体育组随机抽取了10名参赛学生的成绩,将这组数据整理后制成统计表:
一分钟跳绳个数(个) 141 144 145 146
学生人数(名) 5 2 1 2
则关于这组数据的结论正确的是( )
A.平均数是144 B.众数是141 C.中位数是144.5 D.方差是5.4
7.若一组数据2,0,1,x,3的平均数是2,则这组数据的方差是( )
A.1 B.2 C.3 D.4
二、填空题
8.甲、乙两人在100米短跑训练中,某5次的平均成绩相等,甲的方差是0.14,乙的方差是0.06,这5次短跑训练成绩较稳定的是__________.(填“甲”或“乙”)
9.有一组数据如下:2,3,,5,6,它们的平均数是4,则这组数据的方差是_______.
10.一组数据2,x,1,3,5,4,若这组数的中位数是3,则这组数的方差是_________.
11.若八个数据,,,…,的平均数为8,方差为1,则,,…,的平均数为___________,方差为___________.
三、解答题
12.某校九年级两个班各选派6名学生参加“垃圾分类知识竞赛”,各参赛选手的成绩(单位:分)如下(满分100分):
九(1)班:87,91,91,92,94,96;
九(2)班:84,88,90,90,91,97.
(1)九(1)班参赛选手成绩的中位数为__________分,众数是_________分.
(2)求九(2)班参赛选手成绩的方差.
13.甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩/环 中位数/环 众数/环 方差
甲 a 7 7 12
乙 7 b 8 c
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
14.某校八年级(1)班的学生利用春节寒假期间参加社会实践活动,到“山东惠民鑫诚农业科技园”了解大棚热带水果的生长情况.他们分两组对柠檬树的长势进行观察测量,分別收集到10株柠檬树的高度,记录如下(单位:厘米):
第一组:132,139,145,155,160,154,160,128,156,141
第二组:151,156,144,146,140,153,137,147,150,146
根据以上数据,回答下列问题:
(1)第一组这10株柠檬树高度的平均数是_________;中位数是_________,众数是_________;
(2)小明同学计算出第一组的方差为,请你计算第二组的方差,并说明哪一组柠檬树长势比较整齐.
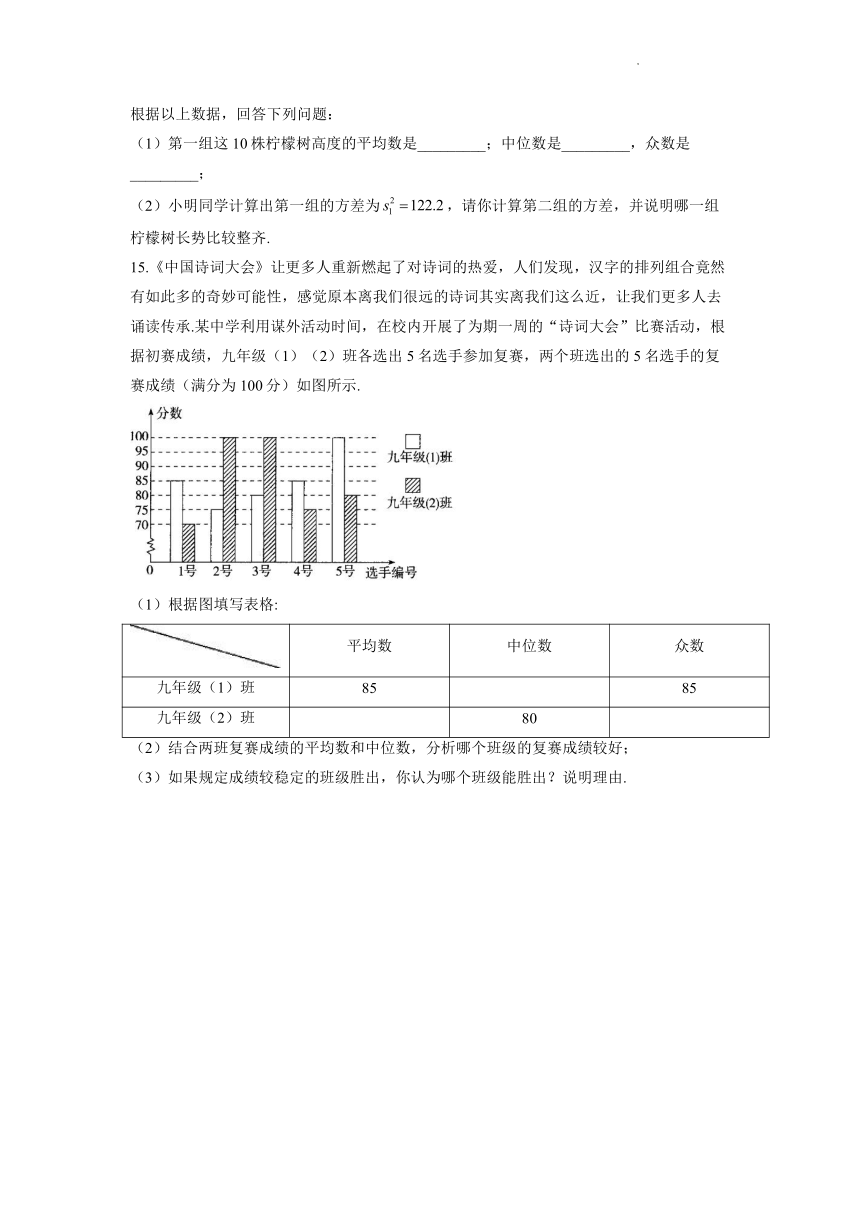
15.《中国诗词大会》让更多人重新燃起了对诗词的热爱,人们发现,汉字的排列组合竟然有如此多的奇妙可能性,感觉原本离我们很远的诗词其实离我们这么近,让我们更多人去诵读传承.某中学利用谋外活动时间,在校内开展了为期一周的“诗词大会”比赛活动,根据初赛成绩,九年级(1)(2)班各选出5名选手参加复赛,两个班选出的5名选手的复赛成绩(满分为100分)如图所示.
(1)根据图填写表格:
平均数 中位数 众数
九年级(1)班 85 85
九年级(2)班 80
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)如果规定成绩较稳定的班级胜出,你认为哪个班级能胜出?说明理由.
参考答案
1.答案:A
解析:,方差越小,波动越小,越整齐.
2.答案:D
解析:
3.答案:D
解析:(分),
(分),
,
.
乙平均分高,成绩不稳定.
4.答案:C
解析:由题意知,这组数据为3,8,11,a,b,c,其平均数为7,则,,故选C.
5.答案:B
解析:
6.答案:B
解析:本题考查平均数、众数、中位数、方差.平均数;众数是141;中位数是;方差,故选B.
7.答案:B
解析:
8.答案:乙
解析:
9.答案:2
解析:2,3,,5,6,它们的平均数是4,则这五个数据的和为20,,
10.答案:
解析:由于数据2,x,1,3,5,4的中位数是3,故,因此这组数据的平均数为,所以这组数据的方差为.
11.答案:17,4
解析:当一组数据同时扩大(或缩小)为原来n倍(或),或者增加或减少相同量时,其平均值随之扩大(或缩小)为原来n倍(或),或者增加或减少相同量.当一组数据同时扩大(或缩小)为原来n倍(或),其方差对应扩大或缩小为原来倍(或),而一组数据增加或减少相同量时,方差保持不变.本题中数据每个都先扩大了2倍,然后再增加了1,所以平均数对应扩大2倍再加1得到17,方差对应扩大2的平方倍得到4.
12.答案:(1)九(1)班参赛选手成绩的中位数为(分),众数是91分.
故答案为91.5,91.
(2)九(2)班参赛选手成绩的平均数是(分),
则方差是.
解析:
13.答案:(1)甲的平均成绩(环).
乙射击的成绩从小到大重新排列为3,4,6,7,7,8,8,8,9,10,
乙射击成绩的中位数(环),
其方差
.
(2)从平均成绩看甲、乙两人的成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多,从方差看甲的成绩比乙的成绩稳定.综合以上各因素,若选派一名队员参加比赛的话,可选择乙参赛,因为乙获得高分的可能性更大.
解析:
14.答案:(1)第一组这10株柠檬树高度的平均数是.
把这些数据从小到大排列为128、132、139、141、145、154、155、156、160、160,
最中间的两个数是145和154,则中位数是.
160出现了2次,出现的次数最多,则众数是160.
(2)∵第二组这10株柠檬树高度的平均数是,
,
,
∴第二组柠檬树长势比较整齐.
解析:
15.答案:(1)将九年级(1)班5位同学的成绩按从小到大的顺序排列为75,80,85,85,100,∴中位数为85.
九年级(2)班5位同学的成绩分别为70,100,100,75,80.
∴九年级(2)班这5位同学的成绩的平均数为,众数为100.
补全表格如下:
平均数 中位数 众数
九年级(1)班 85 85 85
九年级(2)班 85 80 100
(2)九年级(1)班的复赛成绩较好.
理由:∵两个班的平均数相同,九年级(1)班的中位数高,
∴九年级(1)班的复赛成绩较好.
(3)九年级(1)班能胜出.理由如下:
设九年级(1)班成绩的方差为,九年级(2)班成绩的方差为,则;
,
∵,∴九年级(1)班的复赛成绩较稳定,能胜出.
解析:
20.2 数据的波动程度
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某校举行健美操比赛,甲、乙两个班选20名学生参加比赛,两个班参赛学生的平均身高都是1.65米,其方差分别是,,则参赛学生身高比较整齐的班级是( )
A.甲班 B.乙班 C.同样整齐 D.无法确定
2.对于一组统计数据3,3,6,5,3下列说法正确的是( )
A.中位数是6 B.平均数是5 C.方差是1.7 D.众数是3
3.下图是甲、乙两同学五次数学测试成绩的折线图.比较甲、乙的成绩,下列说法正确的是( )
A.甲平均分高,成绩稳定 B.甲平均分高,成绩不稳定
C.乙平均分高,成绩稳定 D.乙平均分高,成绩不稳定
4.已知一组数据的方差,则的值为( )
A.22 B.21 C.20 D.7
5.在庆祝中国共产党成立100周年的“红色记忆”校园歌咏比赛中,15个参赛班级按照成绩(成绩各不相同)取前7名进入决赛,小红知道了自己班级的比赛成绩,如果要判断自己的班级能否进入决赛,还需要知道这15个参赛班级成绩的( )
A.平均数 B.中位数 C.众数 D.方差
6.为调动学生参与体育锻炼的积极性,某校组织了一分钟跳绳比赛活动,体育组随机抽取了10名参赛学生的成绩,将这组数据整理后制成统计表:
一分钟跳绳个数(个) 141 144 145 146
学生人数(名) 5 2 1 2
则关于这组数据的结论正确的是( )
A.平均数是144 B.众数是141 C.中位数是144.5 D.方差是5.4
7.若一组数据2,0,1,x,3的平均数是2,则这组数据的方差是( )
A.1 B.2 C.3 D.4
二、填空题
8.甲、乙两人在100米短跑训练中,某5次的平均成绩相等,甲的方差是0.14,乙的方差是0.06,这5次短跑训练成绩较稳定的是__________.(填“甲”或“乙”)
9.有一组数据如下:2,3,,5,6,它们的平均数是4,则这组数据的方差是_______.
10.一组数据2,x,1,3,5,4,若这组数的中位数是3,则这组数的方差是_________.
11.若八个数据,,,…,的平均数为8,方差为1,则,,…,的平均数为___________,方差为___________.
三、解答题
12.某校九年级两个班各选派6名学生参加“垃圾分类知识竞赛”,各参赛选手的成绩(单位:分)如下(满分100分):
九(1)班:87,91,91,92,94,96;
九(2)班:84,88,90,90,91,97.
(1)九(1)班参赛选手成绩的中位数为__________分,众数是_________分.
(2)求九(2)班参赛选手成绩的方差.
13.甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩/环 中位数/环 众数/环 方差
甲 a 7 7 12
乙 7 b 8 c
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
14.某校八年级(1)班的学生利用春节寒假期间参加社会实践活动,到“山东惠民鑫诚农业科技园”了解大棚热带水果的生长情况.他们分两组对柠檬树的长势进行观察测量,分別收集到10株柠檬树的高度,记录如下(单位:厘米):
第一组:132,139,145,155,160,154,160,128,156,141
第二组:151,156,144,146,140,153,137,147,150,146
根据以上数据,回答下列问题:
(1)第一组这10株柠檬树高度的平均数是_________;中位数是_________,众数是_________;
(2)小明同学计算出第一组的方差为,请你计算第二组的方差,并说明哪一组柠檬树长势比较整齐.
15.《中国诗词大会》让更多人重新燃起了对诗词的热爱,人们发现,汉字的排列组合竟然有如此多的奇妙可能性,感觉原本离我们很远的诗词其实离我们这么近,让我们更多人去诵读传承.某中学利用谋外活动时间,在校内开展了为期一周的“诗词大会”比赛活动,根据初赛成绩,九年级(1)(2)班各选出5名选手参加复赛,两个班选出的5名选手的复赛成绩(满分为100分)如图所示.
(1)根据图填写表格:
平均数 中位数 众数
九年级(1)班 85 85
九年级(2)班 80
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)如果规定成绩较稳定的班级胜出,你认为哪个班级能胜出?说明理由.
参考答案
1.答案:A
解析:,方差越小,波动越小,越整齐.
2.答案:D
解析:
3.答案:D
解析:(分),
(分),
,
.
乙平均分高,成绩不稳定.
4.答案:C
解析:由题意知,这组数据为3,8,11,a,b,c,其平均数为7,则,,故选C.
5.答案:B
解析:
6.答案:B
解析:本题考查平均数、众数、中位数、方差.平均数;众数是141;中位数是;方差,故选B.
7.答案:B
解析:
8.答案:乙
解析:
9.答案:2
解析:2,3,,5,6,它们的平均数是4,则这五个数据的和为20,,
10.答案:
解析:由于数据2,x,1,3,5,4的中位数是3,故,因此这组数据的平均数为,所以这组数据的方差为.
11.答案:17,4
解析:当一组数据同时扩大(或缩小)为原来n倍(或),或者增加或减少相同量时,其平均值随之扩大(或缩小)为原来n倍(或),或者增加或减少相同量.当一组数据同时扩大(或缩小)为原来n倍(或),其方差对应扩大或缩小为原来倍(或),而一组数据增加或减少相同量时,方差保持不变.本题中数据每个都先扩大了2倍,然后再增加了1,所以平均数对应扩大2倍再加1得到17,方差对应扩大2的平方倍得到4.
12.答案:(1)九(1)班参赛选手成绩的中位数为(分),众数是91分.
故答案为91.5,91.
(2)九(2)班参赛选手成绩的平均数是(分),
则方差是.
解析:
13.答案:(1)甲的平均成绩(环).
乙射击的成绩从小到大重新排列为3,4,6,7,7,8,8,8,9,10,
乙射击成绩的中位数(环),
其方差
.
(2)从平均成绩看甲、乙两人的成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多,从方差看甲的成绩比乙的成绩稳定.综合以上各因素,若选派一名队员参加比赛的话,可选择乙参赛,因为乙获得高分的可能性更大.
解析:
14.答案:(1)第一组这10株柠檬树高度的平均数是.
把这些数据从小到大排列为128、132、139、141、145、154、155、156、160、160,
最中间的两个数是145和154,则中位数是.
160出现了2次,出现的次数最多,则众数是160.
(2)∵第二组这10株柠檬树高度的平均数是,
,
,
∴第二组柠檬树长势比较整齐.
解析:
15.答案:(1)将九年级(1)班5位同学的成绩按从小到大的顺序排列为75,80,85,85,100,∴中位数为85.
九年级(2)班5位同学的成绩分别为70,100,100,75,80.
∴九年级(2)班这5位同学的成绩的平均数为,众数为100.
补全表格如下:
平均数 中位数 众数
九年级(1)班 85 85 85
九年级(2)班 85 80 100
(2)九年级(1)班的复赛成绩较好.
理由:∵两个班的平均数相同,九年级(1)班的中位数高,
∴九年级(1)班的复赛成绩较好.
(3)九年级(1)班能胜出.理由如下:
设九年级(1)班成绩的方差为,九年级(2)班成绩的方差为,则;
,
∵,∴九年级(1)班的复赛成绩较稳定,能胜出.
解析:
