2021—2022学年人教版数学八年级下册19.2.3一次函数与方程、不等式巩固练习(word版、含解析)
文档属性
| 名称 | 2021—2022学年人教版数学八年级下册19.2.3一次函数与方程、不等式巩固练习(word版、含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 479.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 20:56:46 | ||
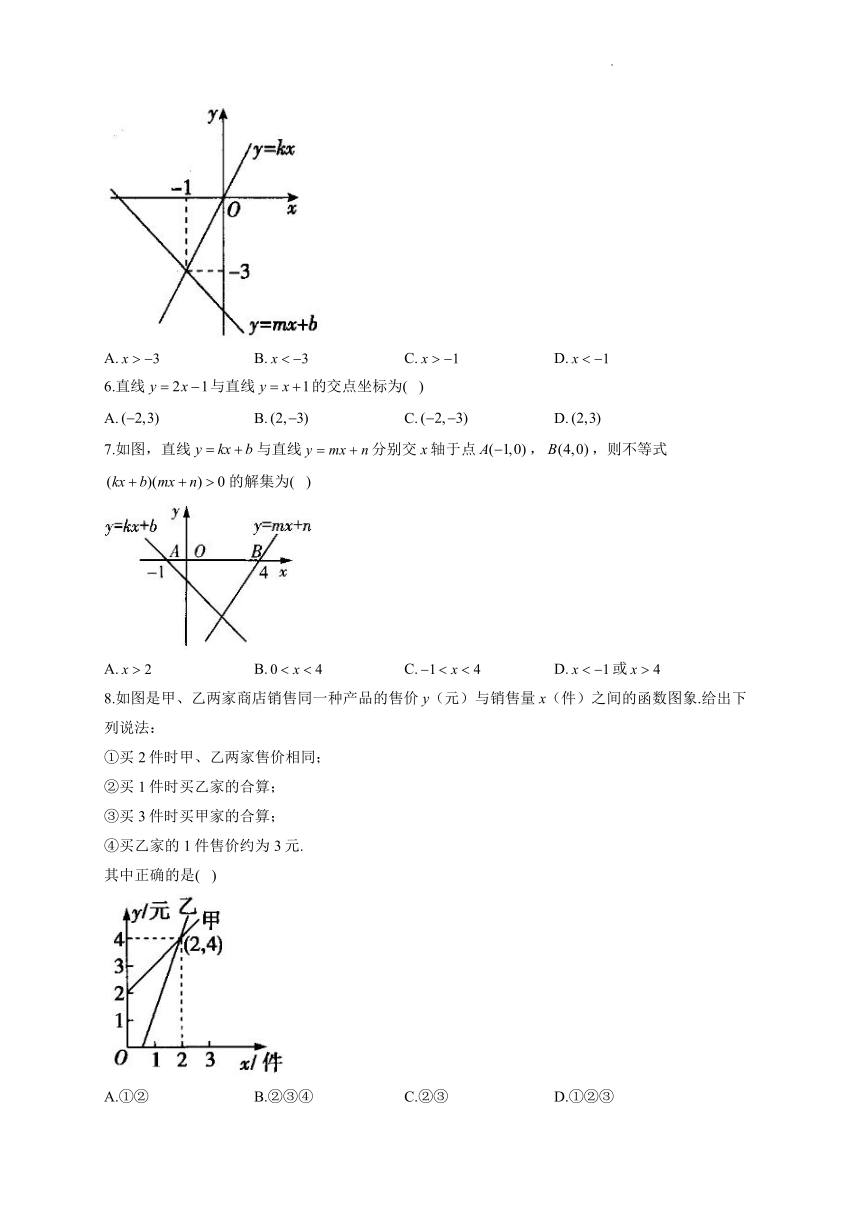
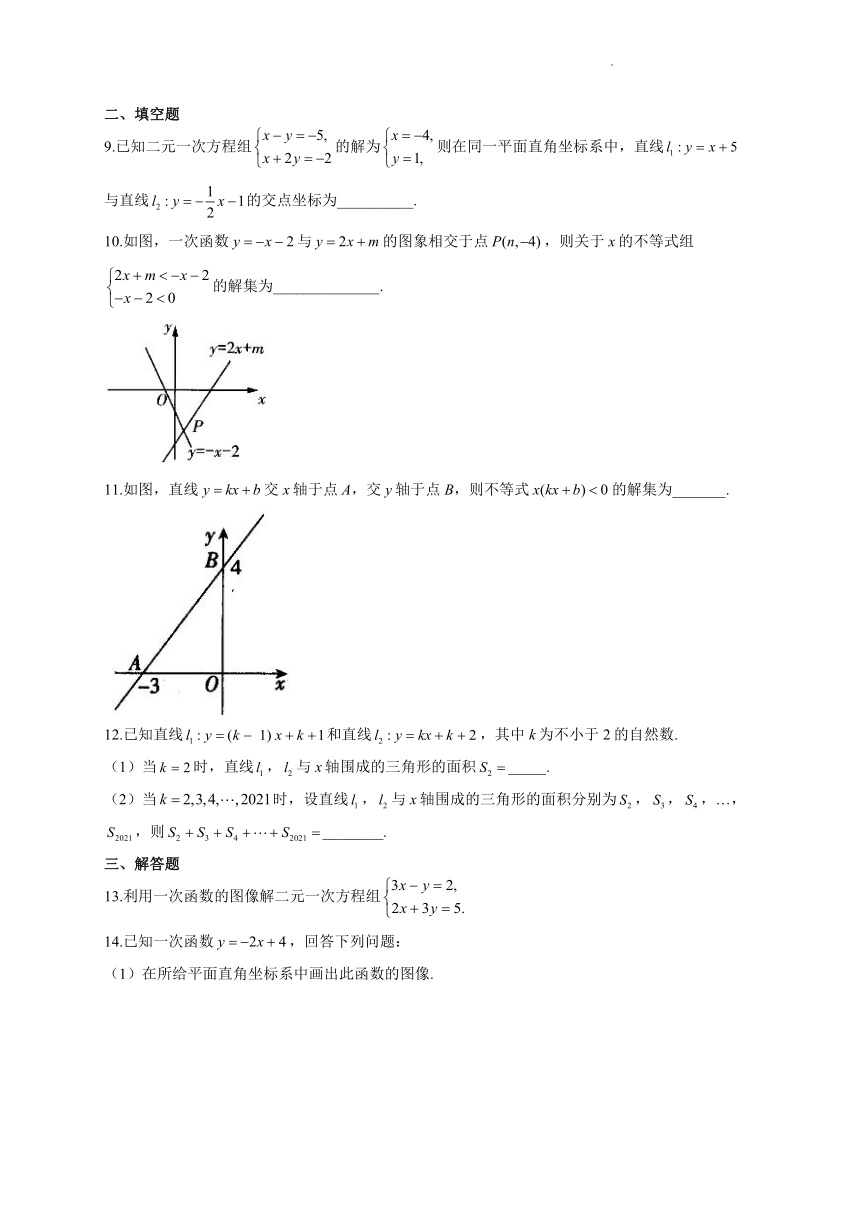
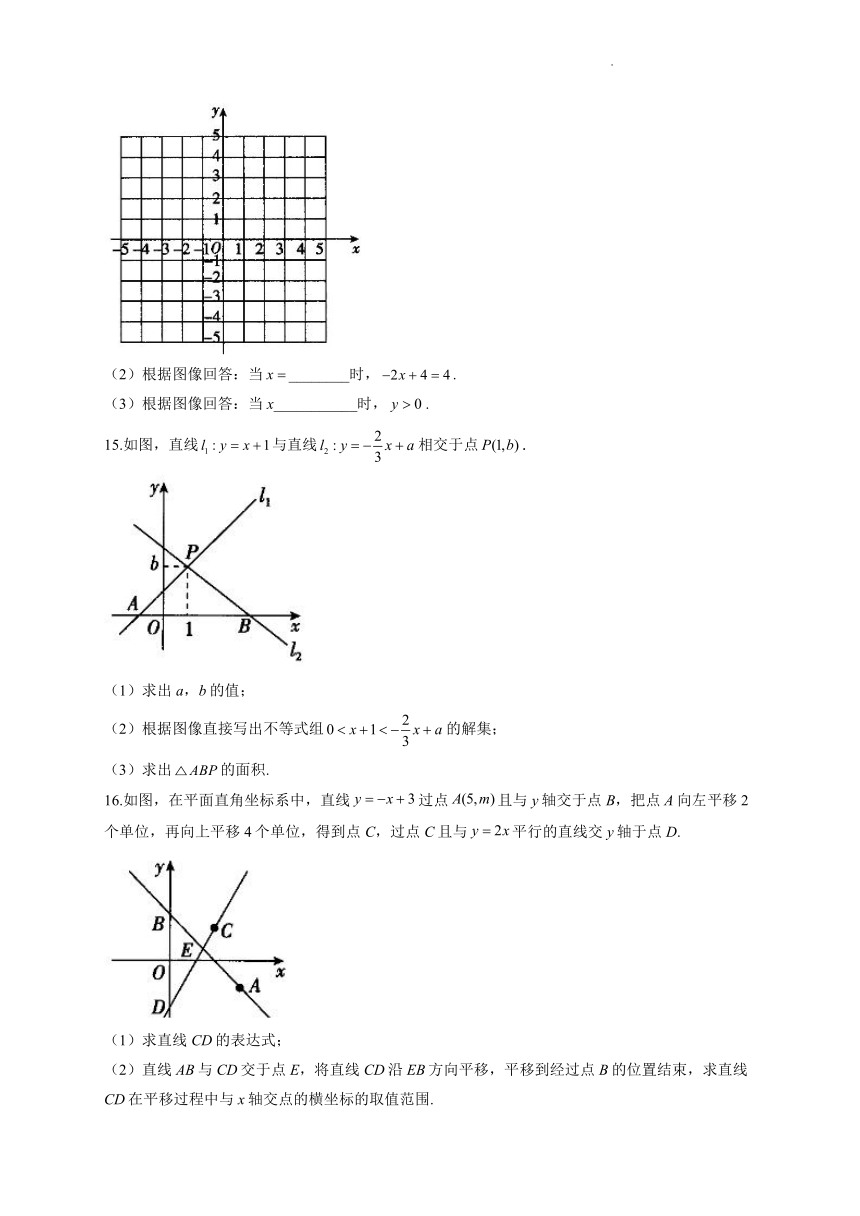
图片预览


文档简介
2021-2022学年八年级下册数学巩固练习(人教版)
19.2.3 一次函数与方程、不等式
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知方程的解是,则直线与直线的交点坐标是( )
A. B. C. D.
2.已知一次函数与的图象如图,则关于x与y的二元一次方程组的解的个数为( )
A.0个 B.1个 C.2个 D.无数个
3.数形结合是解决数学问题常用的思想方法.如图,直线和直线相交于点P,根据图像可知,方程的解是( )
A. B. C. D.
4.一次函数(k,b是常数,)的图像如图所示,则不等式的解集是( )
A. B. C. D.
5.函数与在同一平面直角坐标系中的图像如图所示,则关于x的不等式的解集为( )
A. B. C. D.
6.直线与直线的交点坐标为( )
A. B. C. D.
7.如图,直线与直线分别交x轴于点,,则不等式的解集为( )
A. B. C. D.或
8.如图是甲、乙两家商店销售同一种产品的售价y(元)与销售量x(件)之间的函数图象.给出下列说法:
①买2件时甲、乙两家售价相同;
②买1件时买乙家的合算;
③买3件时买甲家的合算;
④买乙家的1件售价约为3元.
其中正确的是( )
A.①② B.②③④ C.②③ D.①②③
二、填空题
9.已知二元一次方程组的解为则在同一平面直角坐标系中,直线与直线的交点坐标为__________.
10.如图,一次函数与的图象相交于点,则关于x的不等式组的解集为______________.
11.如图,直线交x轴于点A,交y轴于点B,则不等式的解集为_______.
12.已知直线和直线,其中k为不小于2的自然数.
(1)当时,直线,与x轴围成的三角形的面积_____.
(2)当时,设直线,与x轴围成的三角形的面积分别为,,,…,,则________.
三、解答题
13.利用一次函数的图像解二元一次方程组
14.已知一次函数,回答下列问题:
(1)在所给平面直角坐标系中画出此函数的图像.
(2)根据图像回答:当________时,.
(3)根据图像回答:当x___________时,.
15.如图,直线与直线相交于点.
(1)求出a,b的值;
(2)根据图像直接写出不等式组的解集;
(3)求出的面积.
16.如图,在平面直角坐标系中,直线过点且与y轴交于点B,把点A向左平移2个单位,再向上平移4个单位,得到点C,过点C且与平行的直线交y轴于点D.
(1)求直线CD的表达式;
(2)直线AB与CD交于点E,将直线CD沿EB方向平移,平移到经过点B的位置结束,求直线CD在平移过程中与x轴交点的横坐标的取值范围.
参考答案
1.答案:C
解析:方程的解是,,直线与直线的交点坐标为.
2.答案:A
解析:因为一次函数与的图像是两条互相平行的直线,所以关于x与y的二元一次方程组无解.故选A.
3.答案:A
解析:直线和直线相交于点,
方程的解为.故选A.
4.答案:D
解析:由题图可得函数的图像经过点,并且函数值y随x的增大而减小,所以当时,函数值y大于0,即不等式的解集是.故选D.
5.答案:C
解析:根据图像可知,直线与的交点坐标为,则关于x的不等式的解集为.故选C.
6.答案:D
解析:由解得
直线与直线的交点坐标为.
故选D.
7.答案:C
解析:不等式等价于直线与直线同时在x轴上方或同时在x轴下方,因为直线与直线分别交x轴于点,,观察题中图象可知,不等式的解集为.故选C.
8.答案:D
解析:由题中图象,可知当时,,故买2件时甲、乙两家售价相同,故①正确;当时,,所以此时购买乙家的合算,故②正确;当时,,所以此时购买甲家的合算,故③正确;买乙家的1件售价约为1元,故④错误.故选D.
9.答案:
解析:因为二元一次方程组的解为所以直线与直线的交点坐标为.
10.答案:
解析:一次函数的图象过点,,解得,,又与x轴的交点是,结合题中图象,易得关于x的不等式组的解集为.
11.答案:
解析:不等式化为或利用函数图象可得无解,的解集为,所以不等式的解集为.
12.答案:(1)1(2)
解析:当时,有,解得,
直线与x轴的交点坐标为,同理可得直线与x轴的交点坐标为,两直线与x轴交点间的距离.
联立直线,表达式得解得直线,的交点坐标为.
13.答案:由,得;由,
得.在平面直角坐标系中,
画出直线和,如图所示:
由图像可知两直线的交点坐标为,从而得到原方程组的解为
解析:
14.答案:(1)如图所示:
(2)当时,.故答案为0.
(3)当时,.故答案为.
解析:
15.答案:(1)把代入,可得,即,把,代入,可得,解得.
(2)把代入,可得,由图像可得不等式组的解集为.
(3)由(1)得直线把代入可得,即,把代入,可得,即,的面积为.
解析:
16.答案:(1)点在直线上,
,即.
点A向左平移2个单位,再向上平移4个单位,
得到点C,.
直线CD与直线平行,
设直线CD的表达式为.
把代入得,解得,
直线CD的表达式为.
(2)将代入得,即,
直线CD平移到点B时的表达式为.令,得,即直线与x轴的交点坐标为.
将代入得,即直线CD平移前x轴的交点坐标为.
直线CD在平移过程中与x轴交点的横坐标的取值范围是.
解析:
19.2.3 一次函数与方程、不等式
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知方程的解是,则直线与直线的交点坐标是( )
A. B. C. D.
2.已知一次函数与的图象如图,则关于x与y的二元一次方程组的解的个数为( )
A.0个 B.1个 C.2个 D.无数个
3.数形结合是解决数学问题常用的思想方法.如图,直线和直线相交于点P,根据图像可知,方程的解是( )
A. B. C. D.
4.一次函数(k,b是常数,)的图像如图所示,则不等式的解集是( )
A. B. C. D.
5.函数与在同一平面直角坐标系中的图像如图所示,则关于x的不等式的解集为( )
A. B. C. D.
6.直线与直线的交点坐标为( )
A. B. C. D.
7.如图,直线与直线分别交x轴于点,,则不等式的解集为( )
A. B. C. D.或
8.如图是甲、乙两家商店销售同一种产品的售价y(元)与销售量x(件)之间的函数图象.给出下列说法:
①买2件时甲、乙两家售价相同;
②买1件时买乙家的合算;
③买3件时买甲家的合算;
④买乙家的1件售价约为3元.
其中正确的是( )
A.①② B.②③④ C.②③ D.①②③
二、填空题
9.已知二元一次方程组的解为则在同一平面直角坐标系中,直线与直线的交点坐标为__________.
10.如图,一次函数与的图象相交于点,则关于x的不等式组的解集为______________.
11.如图,直线交x轴于点A,交y轴于点B,则不等式的解集为_______.
12.已知直线和直线,其中k为不小于2的自然数.
(1)当时,直线,与x轴围成的三角形的面积_____.
(2)当时,设直线,与x轴围成的三角形的面积分别为,,,…,,则________.
三、解答题
13.利用一次函数的图像解二元一次方程组
14.已知一次函数,回答下列问题:
(1)在所给平面直角坐标系中画出此函数的图像.
(2)根据图像回答:当________时,.
(3)根据图像回答:当x___________时,.
15.如图,直线与直线相交于点.
(1)求出a,b的值;
(2)根据图像直接写出不等式组的解集;
(3)求出的面积.
16.如图,在平面直角坐标系中,直线过点且与y轴交于点B,把点A向左平移2个单位,再向上平移4个单位,得到点C,过点C且与平行的直线交y轴于点D.
(1)求直线CD的表达式;
(2)直线AB与CD交于点E,将直线CD沿EB方向平移,平移到经过点B的位置结束,求直线CD在平移过程中与x轴交点的横坐标的取值范围.
参考答案
1.答案:C
解析:方程的解是,,直线与直线的交点坐标为.
2.答案:A
解析:因为一次函数与的图像是两条互相平行的直线,所以关于x与y的二元一次方程组无解.故选A.
3.答案:A
解析:直线和直线相交于点,
方程的解为.故选A.
4.答案:D
解析:由题图可得函数的图像经过点,并且函数值y随x的增大而减小,所以当时,函数值y大于0,即不等式的解集是.故选D.
5.答案:C
解析:根据图像可知,直线与的交点坐标为,则关于x的不等式的解集为.故选C.
6.答案:D
解析:由解得
直线与直线的交点坐标为.
故选D.
7.答案:C
解析:不等式等价于直线与直线同时在x轴上方或同时在x轴下方,因为直线与直线分别交x轴于点,,观察题中图象可知,不等式的解集为.故选C.
8.答案:D
解析:由题中图象,可知当时,,故买2件时甲、乙两家售价相同,故①正确;当时,,所以此时购买乙家的合算,故②正确;当时,,所以此时购买甲家的合算,故③正确;买乙家的1件售价约为1元,故④错误.故选D.
9.答案:
解析:因为二元一次方程组的解为所以直线与直线的交点坐标为.
10.答案:
解析:一次函数的图象过点,,解得,,又与x轴的交点是,结合题中图象,易得关于x的不等式组的解集为.
11.答案:
解析:不等式化为或利用函数图象可得无解,的解集为,所以不等式的解集为.
12.答案:(1)1(2)
解析:当时,有,解得,
直线与x轴的交点坐标为,同理可得直线与x轴的交点坐标为,两直线与x轴交点间的距离.
联立直线,表达式得解得直线,的交点坐标为.
13.答案:由,得;由,
得.在平面直角坐标系中,
画出直线和,如图所示:
由图像可知两直线的交点坐标为,从而得到原方程组的解为
解析:
14.答案:(1)如图所示:
(2)当时,.故答案为0.
(3)当时,.故答案为.
解析:
15.答案:(1)把代入,可得,即,把,代入,可得,解得.
(2)把代入,可得,由图像可得不等式组的解集为.
(3)由(1)得直线把代入可得,即,把代入,可得,即,的面积为.
解析:
16.答案:(1)点在直线上,
,即.
点A向左平移2个单位,再向上平移4个单位,
得到点C,.
直线CD与直线平行,
设直线CD的表达式为.
把代入得,解得,
直线CD的表达式为.
(2)将代入得,即,
直线CD平移到点B时的表达式为.令,得,即直线与x轴的交点坐标为.
将代入得,即直线CD平移前x轴的交点坐标为.
直线CD在平移过程中与x轴交点的横坐标的取值范围是.
解析:
