7.4 宇宙航行 课件 (50张PPT)
文档属性
| 名称 | 7.4 宇宙航行 课件 (50张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 9.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-31 10:31:19 | ||
图片预览










文档简介
(共50张PPT)
第七章 万有引力与宇宙航行
第4节 宇宙航行
学习目标
1、知道什么是宇宙速度,理解并记住三个宇宙速度的含义和数值
2、会计算第一宇宙速度
3、知道近地卫星、极地卫星、一般卫星和同步卫星的轨道
4、掌握人造卫星在轨道上运行时线速度、角速度、周期与轨道半径的关系
5、知道卫星如何变轨,会处理卫星的变轨问题
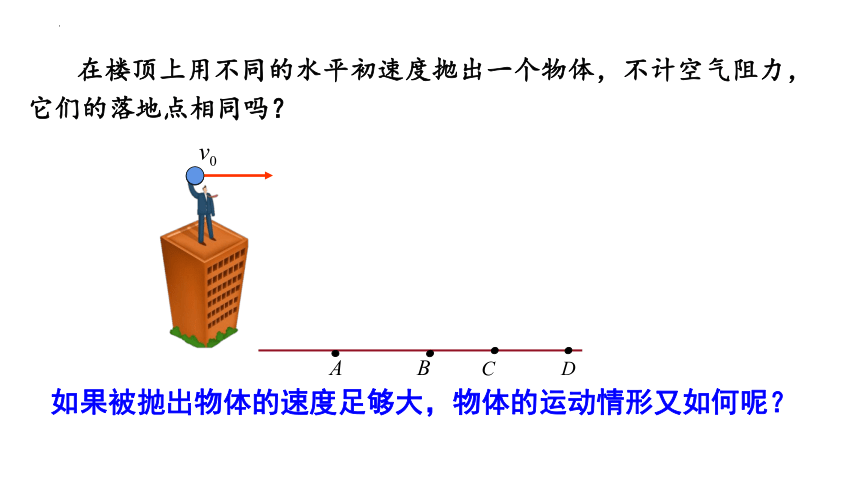
在楼顶上用不同的水平初速度抛出一个物体,不计空气阻力,它们的落地点相同吗?
如果被抛出物体的速度足够大,物体的运动情形又如何呢?
那么物体初速度达到多大时就可以发射成为一颗人造卫星呢
在1687年出版的《自然哲学的数学原理》中,牛顿曾设想,从高山上用不同的水平速度抛出物体,速度一次比一次大,则落点一次比一次远,如果速度足够大,物体就不再落到地面上来,它将绕地球运动,成为一颗人造地球卫星。
牛顿的设想
问题1:按牛顿的设想,在忽略空气阻力的情况下,物体如果刚好不落地,它将怎样运动?
问题2:物体绕地球做圆周运动的向心力由什么力提供?
由地球对物体的万有引力提供
匀速圆周运动
建立模型
刚好不落回地面的最小水平抛出速度
方法1:物体在地表附近绕地球做匀速圆周运动,地球对物体的万有引力提供向心力
方法2:物体在地表附近绕地球做匀速圆周运动,重力提供向心力
已知地球的质量为M = 6.0×1024 kg,地球半径为R = 6400 km,引力常量为G =6.67×10-11 Nm2/kg2,地球表面附近物体的重力加速度g=9.8m/s
1、地球的第一宇宙速度
一、宇宙速度
2.宇宙速度
(2)第二宇宙速度:当物体的速度大于或等于v2=11.2km/s时,卫星就会脱离地球的吸引,不再绕地球运行。我们把这个速度叫第二宇宙速度。
(3)第三宇宙速度:如果物体的速度等于或大于v3=16.7km/s,物体就摆脱了太阳引力的束缚,飞到太阳系以外的宇宙空间去。这个速度叫第三宇宙速度
(1)第一宇宙速度;能使卫星在地面附近环绕地球作匀速圆周运动所具有的最小发射速度。
v1=7.9km/s 在地面附近做匀速圆周运动(近地卫星)
7.9 km/s<v<11.2 km/s,轨迹是椭圆
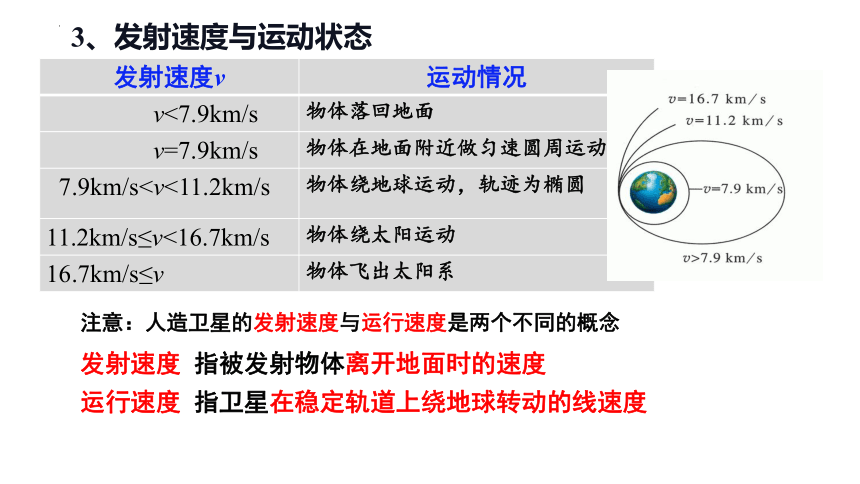
3、发射速度与运动状态
发射速度v 运动情况
v<7.9km/s 物体落回地面
v=7.9km/s 物体在地面附近做匀速圆周运动
7.9km/s11.2km/s≤v<16.7km/s 物体绕太阳运动
16.7km/s≤v 物体飞出太阳系
注意:人造卫星的发射速度与运行速度是两个不同的概念
发射速度 指被发射物体离开地面时的速度
运行速度 指卫星在稳定轨道上绕地球转动的线速度
天体的第一宇宙速度推导方法
已知天体质量为M,天体半径R,天体表面重力加速度g,引力常数G
方法1:近天体环绕时,万有引力提供向心力
方法2:近天体环绕时,重力提供向心力
适用于求解任何天体的第一宇宙速度
练习、若取地球的第一宇宙速度为8 km/s,某行星质量是地球质量的6倍,半径是地球半径的1.5倍,此行星的第一宇宙速度约为 ( )
A.16 km/s B.32 km/s
C.4 km/s D.2 km/s
A
练习、(多选)2020年7月,备受瞩目的火星探测将迎来发射“窗口期”,届时,包括中国“天问一号”、美国“毅力号”和阿联酋“希望号”在内的多国火星探测器,将“同台竞技”奔向火星,在探测器下降与着陆过程中,存在所谓“恐怖7分钟”,即要在7分钟内将探测器的速度从5000m/s降到零。已知地球的质量约为火星质量的10倍,地球的半径约为火星半径的2倍,地球的第一宇宙速度为7.9km/s,地球表面重力加速度g=10m/s2,在恐怖7分钟内,探测器的运动可视为竖直向下的匀变速直线运动。则( )A.火星探测器在恐怖七分钟内处于失重状态 B.火星表面的重力加速度约为2m/s2 C.火星的第一宇宙速度约3.5km/s D.探测器至少要距离火星表面1.05×106m开始减速
CD
练习(多选)第一宇宙速度v1与第二宇宙速度v2的关系是 。已知某星球半径是地球半径R的 ,其表面的重力加速度是地球表面重力加速度g的 ,地球的平均密度为ρ,不计其它星球的影响,则该星球的( )
B.第二宇宙速度为
C.质量为
D.平均密度为
A.第二宇宙速度为
AD
练习、某人在一星球上以速率v竖直上抛一物体,经时间t后,物体以速率v落回手中.已知该星球的半径为R,求该星球上的第一宇宙速度的大小.
解析
据匀变速的规律,该星球表面的重力加速度
由牛顿第二定律:
星球的第一宇宙速度:
练习、如图所示,宇航员站在某质量分布均匀的星球表面一斜坡上P点沿水平方向以初速度v0抛出一个小球,测得小球经时间t落到斜坡上另一点Q,斜面的倾角为θ,已知该星球半径为R,万有引力常量为G,求:(1)该星球的密度;(2)该星球的第一宇宙速度.
(1)该星球的密度为
(2)该星球的第一宇宙速度为
1970年4月24日,我国第一颗人造地球卫星“东方红1号”发射成功。
1957年10月4日,世界上第一颗人造地球卫星发射成功。(前苏联)
二、人造地球卫星
牛顿虽然早就预言了人造地球卫星,但因发射需达到 很大的速度,这对于人类是一个巨大的挑战。直到多级 火箭的研制成功,才为人造地球卫星的发射创造了条件。
康斯坦丁·齐奥尔科夫斯基
(1857-1935前苏联)
“地球是人类的摇篮,但人类不会永远呆在摇篮里。”
人造卫星分类:通信卫星、测地卫星、气象卫星、科学卫星等
自首颗人造地球卫星发射后,人类已经发射了数千颗人造地球卫星,目前在轨有效运行的卫星有上千颗,其中的通信、导航、气象等卫星已极大地改变了人类的生活。
1、人造卫星:是由人类建造,以太空飞行载具如火箭、航天飞机等发射到太空中,环绕地球或其它行星的人造天体。(人造卫星和行星质量相差很大,一般构成中心环绕系统。也就是行星是中心天体,人造卫星围绕行星做圆周运动)
(1)运动轨迹:一般绕地球做匀速圆周运动,
(2)向心力来源:由地球对它的万有引力提供向心力
(3)轨道圆心和地球球心关系:
万有引力指向地心,向心力指向轨道的圆心。因此圆心与地心重合。
(1)赤道轨道:卫星的轨道在赤道平面上,卫星始终处于赤道正上方(一般赤道轨道和同步轨道)。
(2)极地轨道:卫星轨道平面与赤道平面垂直,卫星通过两极上空。
(3)倾斜轨道:卫星轨道和赤道成一定的角度。
3、人造卫星的三类可能轨道:
同步轨道
一般赤道轨道
倾斜轨道
极地轨道
2、人造卫星轨道特点:
思考;人造地球卫星的轨道为什么没有这样的轨道?
F引
F1
F2
极地轨道
赤道轨道
地球同步卫星
倾斜轨道
三、人造卫星运行的规律
1、建构模型——人造卫星绕地球做匀速圆周运动
(r↑ a↓)
最大向心加速度(重力加速度)9.8m/s2 r=R时
(r↑ v↓)
最大环绕速度7.9km/s
r=R时
(r↑ ω↓)
(r↑ T ↑)
最短周期84.8分钟 r=R时
r越大,运动的越慢r越小,运动的越快
2、卫星线速度、角速度、周期、向心加速度与轨道半径的关系
设地球和卫星的质量分别为 M 和 m ,引力常量为G,卫星到地心的距离为r,求卫星运动的加速度a、线速度v、角速度ω、周期T
对第一宇宙速度的再认识:
1、绕地球运动的卫星的最小发射速度
3、卫星绕地球做圆周运动的最大运行(环绕)速度
2、卫星绕近地(r=R)圆轨道的运行(环绕)速度
第一宇宙速度的求解方法
依据万有引力提供向心力,求解卫星绕近地圆轨道(近地卫星r=R)的线速度,就是第一宇宙速度
练习、如图所示,若两颗人造卫星a和b均绕地球做匀速圆周运动,a、b到地心O的距离分别为r1、r2,线速度大小分别为v1、v2,则 ( )
A
练习、(多选)如图所示是在同一轨道平面上的三颗不同的人造地球卫星,关于各物理量的关系,下列说法正确的是( )
A.根据v= ,可知vA<vB<vC
B.根据万有引力定律,可知卫星所受地球引力FA>FB>FC
C.角速度ωA>ωB>ωC
D.向心加速度aA>aB>aC
CD
四、近地卫星和地球同步卫星
1、近地卫星具有
最小轨道半径r=R=6.4 ×103km
最大绕行速度V=________=__________=7.9km/s
最小绕行周期T=84.8min
无论何种卫星,它的轨道平面必定经过地球球心
(1)定义:位于赤道正上方相对于地面静止的卫星,也称静止卫星。周期与地球自转周期相同(T=24h)。
(2)特点
邹平上空有同步卫星吗?
2、地球同步卫星
练习、(2020·天津卷)北斗问天,国之夙愿。我国北斗三号系统的收官之星是地球静止轨道卫星,其轨道半径约为地球半径的7倍。与近地轨道卫星相比,地球静止轨道卫星的( )
A.周期大 B.线速度大
C.角速度大 D.加速度大
A
练习、(多选)我国“中星11号”商业通信卫星是一颗同步卫星,它定点于东经98.2度的赤道上空,关于这颗卫星的说法正确的是( )
A.运行速度大于7.9 km/s
B.离地面高度一定,相对地面静止
C.绕地球运行的角速度比月球绕地球运行的角速度大
D.向心加速度与静止在赤道上物体的向心加速度大小相等
BC
3.四个比较:(请熟知)
(1)同步卫星的周期、轨道平面、高度、线速度、角速度、绕行方向均是固定不变的,常用于无线电通信,故又称通信卫星。(只能在赤道的正上方)
(2)极地卫星运行时每圈都经过南北两极,由于地球自转,极地卫星可以实现全球覆盖。
(3)近地卫星是在地球表面附近绕地球做匀速圆周运动的卫星,其运行的轨道半径可近似认为等于地球的半径,其运行线速度约为7.9 km/s。
(4)赤道上的物体随地球自转而做匀速圆周运动,由万有引力和地面支持力的合力充当向心力。
它的运动规律不同于卫星,但它的周期、角速度与同步卫星相等,就是地球自转的周期、加速度。
近地卫星、同步卫星:F万=F心;赤道物体:F万-F支=F心 (F心≠F万);
①近地卫星与同步卫星(都是卫星)
高轨低速长周期 r同>r近;a、v、ω :近地卫星>同步卫星;T:近<同;
② 同步卫星与赤道上物体(周期相同)
同轴转动模型r同>r赤; T同=T物=24h(ω同); a、v:同步卫星>赤道物体
③ 近地卫星与赤道物体(半径相同)
T近 赤道物体
④三类物体匀速圆周运动的比较:
r同>r近=r物; T近V同>V物
a近>a同>a物;F心近>F心同>F心物;F万物=F万近>F万同(质量相同)
4、近地卫星、同步卫星及赤道上物体的运行问题
课后作业-4
练习、(多选)如图所示,A为地面上的待发射卫星,B为近地圆轨道卫星,C为地球同步卫星。三颗卫星的线速度大小分别为vA、vB、vC,角速度大小分别为ωA、ωB、ωC,周期分别为TA、TB、TC,向心加速度大小分别为aA、aB、aC,则( )
A.TA=TC>TB B.ωA=ωC>ωB
C.vA>vB>vC D.aB>aC>aA
AD
练习、(多选)地球同步卫星到地心距离为r,运行速度为v1,加速度为a1;地球赤道上的物体随地球自转的加速度为a2,第一宇宙速度为v2,地球半径为R,则下列式子中正确的是( )
AC
五、卫星的变轨问题
解决变轨问题的基本思路:
假设轨道不变,分析由于速度的变化,此时受到的万有引力大小、向心力大小
五、卫星的变轨问题
假设卫星仍在原来轨道,分析由于速度变化,此时提供的向心力(万有引力)与需要的向心力大小关系,进而判断轨道的变化情况。
(1)提供<需要,离心运动,由小轨道变向大轨道
(2)提供>需要,近心运动,由大轨道变向小轨道
F提供=F需要,做圆周运动
F提供<F需要,做离心运动
F提供>F需要,做近心运动
1、基本思路:
1
2
3
P
Q
1 是圆轨道,2 是椭圆轨道,3 是圆轨道
O
1 轨道的Q点,点火加速,到达 2 轨道;
2 轨道的P点,再点火加速,到达 3 轨道;
2 椭圆轨道:
1、3 圆轨道:
综上:
变轨点
变轨点
开普勒第二定律
比较速度关系
离心运动:
五、卫星的变轨问题
1
2
3
P
Q
O
变轨点
变轨点
开普勒第三定律:
比较周期关系
椭圆轨道:
圆轨道:
(比较半径)
(比较半长轴)
综上:
1 是圆轨道,2 是椭圆轨道,3 是圆轨道
五、卫星的变轨问题
1
2
3
P
Q
O
变轨点
变轨点
比较加速度关系
1、3 圆轨道:
1、2 轨道的Q为同一个点:
2、3 轨道的P为同一个点:
综上:
1 是圆轨道,2 是椭圆轨道,3 是圆轨道
五、卫星的变轨问题
⑴判断卫星在不同圆轨道的运行速度大小时,
可根据“越远(高)越慢”的规律判断;
⑵判断卫星在同一椭圆轨道上不同点的速度大小时,可根据开普勒第二定律判断,即离中心天体越远,速度越小;
⑶判断卫星为实现变轨在某点需要加速还是减速时,可根据离心运动或近心运动的条件进行分析;(相切点,速度内小外大)
⑷判断卫星的加速度大小时,可根据 判断.
归纳:判断卫星变轨时速度、加速度、周期变化情况
⑸卫星不同轨道上运行周期的比较由开普勒第三定律判断
练习、(多选)如图所示,若关闭动力的航天飞机在月球引力作用下向月球靠近,并将与空间站在B处对接,已知空间站绕月球做匀速圆周运动的轨道半径为r,周期为T,万有引力常量为G,下列说法中正确的是( )
A. 图中航天飞机正加速飞向B处
B. 航天飞机在B处由椭圆轨道进入
空间站轨道时必须点火减速
C. 根据题中条件可以算出月球质量
D. 根据题中条件可以算出空间站受到月球引力的大小
ABC
练习、(多选)如图所示,卫星a距地球表面的距离为R,卫星b为地球同步卫星,两者都可视为绕地球沿同一方向做匀速圆周运动,某时刻卫星a、b恰好相距最近。已知地球质量为M、半径为R,地球自转的角速度为ω,引力常量为G,则下列说法正确的是( )
A.卫星b的速度小于卫星a的速度B.卫星a、b的发射速度都等于7.9km/s
D.卫星a和卫星b下一次相距最近还需经过
C.卫星b距地球表面的高度为
ACD
六、拉格朗日点
在两个大物体的引力场空间中存在着一些点。在这些点处的小物体可相对于两个大物体基本保持静止,这些点称为拉格朗日点。(与M2以相同周期绕M1运动)
这些点的存在由瑞士数学家欧拉于1767年推算出前三个,法国数学家拉格朗日于1772年推导证明剩下两个。
在每个由两大天体构成的系统中,按推论有5个拉格朗日点,但只有两个是稳定的(图中L4、L5),即小物体在该点处即使受外界引力的摄扰,仍然有保持在原来位置处的倾向。每个稳定点同两大物体所在的点构成一个等边三角形。
练习、(多选) 2018年5月25日,探月工程嫦娥四号任务“鹊桥”中继卫星成功实施近月制动,进入月球至地月拉格朗日L2点的转移轨道.当“鹊桥”位于拉格朗日点(如图中的L1、L2、L3、L4、L5所示,人们称为地月系统拉格朗日点)上时,会在月球与地球的共同引力作用下,几乎不消耗燃料而保持与月球同步绕地球做圆周运动,下列说法正确的是(月球的自转周期等于月球绕地球运动的周期)( )
A.“鹊桥”位于L2点时,“鹊桥”绕地球运动的周期
和月球的自转周期相等
B.“鹊桥”位于L2点时,“鹊桥”绕地球运动的
向心加速度大于月球绕地球运动的向心加速度
C.L3和L2到地球中心的距离相等
D.“鹊桥”在L2点所受月球和地球引力的合力比在其余四个点都要大
ABD
练习、(多选)拉格朗日点是小天体在两个大天体的引力作用下基本能保持相对静止的点。如图是日地系统的5个拉格朗日点(L1、L2、L3、L4、L5),设想未来人类在这五个点上都建立了太空站。若不考虑其他天体对太空站的引力,下列说法正确的是( )
BC
A.位于L1点的太空站受力平衡B.位于L2点的太空站的线速度大小大于地球的
线速度大小C.位于L3点的太空站的向心加速度大小大于位于
L1点的太空站的向心加速度大小D.位于L4点的太空站受到的向心力大小等于位于L5点的太空站受到的向心力大小
练习、(2019·河北唐山市第一次模拟)2018年6月14日,我国探月工程嫦娥四号的中继星“鹊桥”顺利进入地月拉格朗日L2点的运行轨道,为地月信息联通搭建“天桥”.如图所示,L2点位于地球与月球中心连线的延长线上,“鹊桥 ”位于该点,在几乎不消耗燃料的情况下与月球同步绕地球做圆周运动,已知地球、月球和“鹊桥”的质量分别为M1、M2、m,地球和月球球心间的距离为R,L2点到月球中心的距离为x,则x满足( )
C
嫦娥奔月
敦煌飞天
六、载人航天与太空探索
14世纪末,明朝的士大夫万户把47枚火箭绑在自己坐的椅子上,两只手各拿一个大风筝。然后叫他的仆人同时点燃所有的火箭,想借火箭的推力飞上月球,然后利用风筝平稳着路,不幸火箭爆炸,万户也为此献出了生命。
六、载人航天与太空探索
康斯坦丁·齐奥尔科夫斯基
(1857-1935前苏联)
“地球是人类的摇篮,但人类不会永远呆在摇篮里。”
多级火箭理论
六、载人航天与太空探索
1961 年 4 月 12 日,苏联航天员加加林进入了东方一号载人飞船。火箭点火起飞,飞船绕地球飞行一圈,历时108 min,然后重返大气层,安全降落在地面,铸就了人类首次进入太空的丰碑。
1969 年 7 月 16 日 9 时 32 分,运载阿波罗 11 号飞船的土星 5 号火箭在美国卡纳维拉尔角点火升空,拉开人类登月这一伟大历史事件的帷幕。7 月 20 日下午 10 时 56 分,指挥长阿姆斯特朗小心翼翼地踏上月面,并说出了那句载入史册的名言 :“对个人来说,这不过是小小的一步,但对人类而言,却是巨大的飞跃。”
六、载人航天与太空探索
钱学森,世界著名科学家,空
气动力学家,中国载人航天奠基人,
“中国科制之父”和“火箭之王”,
由于钱学森回国效力,中国导弹、
原子弹的发射向前推进了至少20年。
曾任美国麻省理工学院和加州理
工学院教授。1950年钱学森回国受
阻,并受美国方面监禁,1955年,
在毛泽东主席和周恩来总理的争取下回到中国。
中国航天之父
中国航天之父:钱学森(1911.12.11-2009.10.31)
六、载人航天与太空探索
2003年10月15日9时,神州五号宇宙飞船在酒泉卫星发射中心成功发射,把中国第一位航天员杨利伟送入太空。
六、载人航天与太空探索
人类一直有“飞天”的梦想,万有引力定律的发现,不仅破解了天上行星的运行规律,也为人类开辟了上天的 理论之路。随着技术的进步,人类迈向太空的脚步越来越 大,越来越坚实。
六、载人航天与太空探索
1957.10.4:第一颗人造卫星(苏联)
1961.4.12:第一次载人飞船(苏联,加加林)
1969.7.16-7.20:第一次登月(美国,阿姆斯特朗)
1970.4.24:中国第一颗人造卫星(东方红一号)
神舟计划:建设自己的空间站
2003.10.15:神舟五号载人飞船(中国,杨利伟)
2021.10.16:神舟十三号载人飞船(翟志刚,王亚平,叶光富,将在太空工作生活六个月)
嫦娥计划:2004年中国开展探月工程
2007.10.24:发射嫦娥一号
2020.11.24:发射嫦娥五号,目前已取样返回
火星计划:2016年立项,开展探测火星工程
2020.7.23:天问一号发射
2021.2.10:被火星捕获
2021.5.15:着陆
2021.5.22:祝融号火星车驶离着陆平台踏上火星表面巡视探测
四.梦想成真
载人航天与太空探索
对地球:v1=7.9km/s (环绕速度)
7.9km/sb.当v ≥11.2km/s时,脱离地球(绕太阳),第二宇宙速度(绕太阳),也称脱离速度
c.当v ≥16.7km/s时,脱离太阳,第三宇宙速度也称逃逸速度
课堂小结:
a.第一宇宙速度:
(对任何天体都适用)
一、宇宙速度(卫星发射)
二、 卫星运行的规律————卫星环绕(卫星运行)
基本思路;1、卫星绕地球做匀速圆周运动,万有引力提供向心力(F提供=F需要)
2、万有引力等于重力
三、同步卫星
1、同步卫星与地面相对静止,与地球自转同步,周期为24h。
2、同步卫星运行方向与地球自转的方向相同。
3、同步卫星定点在赤道上方,离地的高度、运行的速率是唯一确定的。
四、卫星变轨
基本思路:先假设卫星在原来的轨道上,分析此时提供的向心力;运动需要的向心力。如果提供大于需要——近心运动(r变小);提供小于需要——离心运动(r变大)
第七章 万有引力与宇宙航行
第4节 宇宙航行
学习目标
1、知道什么是宇宙速度,理解并记住三个宇宙速度的含义和数值
2、会计算第一宇宙速度
3、知道近地卫星、极地卫星、一般卫星和同步卫星的轨道
4、掌握人造卫星在轨道上运行时线速度、角速度、周期与轨道半径的关系
5、知道卫星如何变轨,会处理卫星的变轨问题
在楼顶上用不同的水平初速度抛出一个物体,不计空气阻力,它们的落地点相同吗?
如果被抛出物体的速度足够大,物体的运动情形又如何呢?
那么物体初速度达到多大时就可以发射成为一颗人造卫星呢
在1687年出版的《自然哲学的数学原理》中,牛顿曾设想,从高山上用不同的水平速度抛出物体,速度一次比一次大,则落点一次比一次远,如果速度足够大,物体就不再落到地面上来,它将绕地球运动,成为一颗人造地球卫星。
牛顿的设想
问题1:按牛顿的设想,在忽略空气阻力的情况下,物体如果刚好不落地,它将怎样运动?
问题2:物体绕地球做圆周运动的向心力由什么力提供?
由地球对物体的万有引力提供
匀速圆周运动
建立模型
刚好不落回地面的最小水平抛出速度
方法1:物体在地表附近绕地球做匀速圆周运动,地球对物体的万有引力提供向心力
方法2:物体在地表附近绕地球做匀速圆周运动,重力提供向心力
已知地球的质量为M = 6.0×1024 kg,地球半径为R = 6400 km,引力常量为G =6.67×10-11 Nm2/kg2,地球表面附近物体的重力加速度g=9.8m/s
1、地球的第一宇宙速度
一、宇宙速度
2.宇宙速度
(2)第二宇宙速度:当物体的速度大于或等于v2=11.2km/s时,卫星就会脱离地球的吸引,不再绕地球运行。我们把这个速度叫第二宇宙速度。
(3)第三宇宙速度:如果物体的速度等于或大于v3=16.7km/s,物体就摆脱了太阳引力的束缚,飞到太阳系以外的宇宙空间去。这个速度叫第三宇宙速度
(1)第一宇宙速度;能使卫星在地面附近环绕地球作匀速圆周运动所具有的最小发射速度。
v1=7.9km/s 在地面附近做匀速圆周运动(近地卫星)
7.9 km/s<v<11.2 km/s,轨迹是椭圆
3、发射速度与运动状态
发射速度v 运动情况
v<7.9km/s 物体落回地面
v=7.9km/s 物体在地面附近做匀速圆周运动
7.9km/s
16.7km/s≤v 物体飞出太阳系
注意:人造卫星的发射速度与运行速度是两个不同的概念
发射速度 指被发射物体离开地面时的速度
运行速度 指卫星在稳定轨道上绕地球转动的线速度
天体的第一宇宙速度推导方法
已知天体质量为M,天体半径R,天体表面重力加速度g,引力常数G
方法1:近天体环绕时,万有引力提供向心力
方法2:近天体环绕时,重力提供向心力
适用于求解任何天体的第一宇宙速度
练习、若取地球的第一宇宙速度为8 km/s,某行星质量是地球质量的6倍,半径是地球半径的1.5倍,此行星的第一宇宙速度约为 ( )
A.16 km/s B.32 km/s
C.4 km/s D.2 km/s
A
练习、(多选)2020年7月,备受瞩目的火星探测将迎来发射“窗口期”,届时,包括中国“天问一号”、美国“毅力号”和阿联酋“希望号”在内的多国火星探测器,将“同台竞技”奔向火星,在探测器下降与着陆过程中,存在所谓“恐怖7分钟”,即要在7分钟内将探测器的速度从5000m/s降到零。已知地球的质量约为火星质量的10倍,地球的半径约为火星半径的2倍,地球的第一宇宙速度为7.9km/s,地球表面重力加速度g=10m/s2,在恐怖7分钟内,探测器的运动可视为竖直向下的匀变速直线运动。则( )A.火星探测器在恐怖七分钟内处于失重状态 B.火星表面的重力加速度约为2m/s2 C.火星的第一宇宙速度约3.5km/s D.探测器至少要距离火星表面1.05×106m开始减速
CD
练习(多选)第一宇宙速度v1与第二宇宙速度v2的关系是 。已知某星球半径是地球半径R的 ,其表面的重力加速度是地球表面重力加速度g的 ,地球的平均密度为ρ,不计其它星球的影响,则该星球的( )
B.第二宇宙速度为
C.质量为
D.平均密度为
A.第二宇宙速度为
AD
练习、某人在一星球上以速率v竖直上抛一物体,经时间t后,物体以速率v落回手中.已知该星球的半径为R,求该星球上的第一宇宙速度的大小.
解析
据匀变速的规律,该星球表面的重力加速度
由牛顿第二定律:
星球的第一宇宙速度:
练习、如图所示,宇航员站在某质量分布均匀的星球表面一斜坡上P点沿水平方向以初速度v0抛出一个小球,测得小球经时间t落到斜坡上另一点Q,斜面的倾角为θ,已知该星球半径为R,万有引力常量为G,求:(1)该星球的密度;(2)该星球的第一宇宙速度.
(1)该星球的密度为
(2)该星球的第一宇宙速度为
1970年4月24日,我国第一颗人造地球卫星“东方红1号”发射成功。
1957年10月4日,世界上第一颗人造地球卫星发射成功。(前苏联)
二、人造地球卫星
牛顿虽然早就预言了人造地球卫星,但因发射需达到 很大的速度,这对于人类是一个巨大的挑战。直到多级 火箭的研制成功,才为人造地球卫星的发射创造了条件。
康斯坦丁·齐奥尔科夫斯基
(1857-1935前苏联)
“地球是人类的摇篮,但人类不会永远呆在摇篮里。”
人造卫星分类:通信卫星、测地卫星、气象卫星、科学卫星等
自首颗人造地球卫星发射后,人类已经发射了数千颗人造地球卫星,目前在轨有效运行的卫星有上千颗,其中的通信、导航、气象等卫星已极大地改变了人类的生活。
1、人造卫星:是由人类建造,以太空飞行载具如火箭、航天飞机等发射到太空中,环绕地球或其它行星的人造天体。(人造卫星和行星质量相差很大,一般构成中心环绕系统。也就是行星是中心天体,人造卫星围绕行星做圆周运动)
(1)运动轨迹:一般绕地球做匀速圆周运动,
(2)向心力来源:由地球对它的万有引力提供向心力
(3)轨道圆心和地球球心关系:
万有引力指向地心,向心力指向轨道的圆心。因此圆心与地心重合。
(1)赤道轨道:卫星的轨道在赤道平面上,卫星始终处于赤道正上方(一般赤道轨道和同步轨道)。
(2)极地轨道:卫星轨道平面与赤道平面垂直,卫星通过两极上空。
(3)倾斜轨道:卫星轨道和赤道成一定的角度。
3、人造卫星的三类可能轨道:
同步轨道
一般赤道轨道
倾斜轨道
极地轨道
2、人造卫星轨道特点:
思考;人造地球卫星的轨道为什么没有这样的轨道?
F引
F1
F2
极地轨道
赤道轨道
地球同步卫星
倾斜轨道
三、人造卫星运行的规律
1、建构模型——人造卫星绕地球做匀速圆周运动
(r↑ a↓)
最大向心加速度(重力加速度)9.8m/s2 r=R时
(r↑ v↓)
最大环绕速度7.9km/s
r=R时
(r↑ ω↓)
(r↑ T ↑)
最短周期84.8分钟 r=R时
r越大,运动的越慢r越小,运动的越快
2、卫星线速度、角速度、周期、向心加速度与轨道半径的关系
设地球和卫星的质量分别为 M 和 m ,引力常量为G,卫星到地心的距离为r,求卫星运动的加速度a、线速度v、角速度ω、周期T
对第一宇宙速度的再认识:
1、绕地球运动的卫星的最小发射速度
3、卫星绕地球做圆周运动的最大运行(环绕)速度
2、卫星绕近地(r=R)圆轨道的运行(环绕)速度
第一宇宙速度的求解方法
依据万有引力提供向心力,求解卫星绕近地圆轨道(近地卫星r=R)的线速度,就是第一宇宙速度
练习、如图所示,若两颗人造卫星a和b均绕地球做匀速圆周运动,a、b到地心O的距离分别为r1、r2,线速度大小分别为v1、v2,则 ( )
A
练习、(多选)如图所示是在同一轨道平面上的三颗不同的人造地球卫星,关于各物理量的关系,下列说法正确的是( )
A.根据v= ,可知vA<vB<vC
B.根据万有引力定律,可知卫星所受地球引力FA>FB>FC
C.角速度ωA>ωB>ωC
D.向心加速度aA>aB>aC
CD
四、近地卫星和地球同步卫星
1、近地卫星具有
最小轨道半径r=R=6.4 ×103km
最大绕行速度V=________=__________=7.9km/s
最小绕行周期T=84.8min
无论何种卫星,它的轨道平面必定经过地球球心
(1)定义:位于赤道正上方相对于地面静止的卫星,也称静止卫星。周期与地球自转周期相同(T=24h)。
(2)特点
邹平上空有同步卫星吗?
2、地球同步卫星
练习、(2020·天津卷)北斗问天,国之夙愿。我国北斗三号系统的收官之星是地球静止轨道卫星,其轨道半径约为地球半径的7倍。与近地轨道卫星相比,地球静止轨道卫星的( )
A.周期大 B.线速度大
C.角速度大 D.加速度大
A
练习、(多选)我国“中星11号”商业通信卫星是一颗同步卫星,它定点于东经98.2度的赤道上空,关于这颗卫星的说法正确的是( )
A.运行速度大于7.9 km/s
B.离地面高度一定,相对地面静止
C.绕地球运行的角速度比月球绕地球运行的角速度大
D.向心加速度与静止在赤道上物体的向心加速度大小相等
BC
3.四个比较:(请熟知)
(1)同步卫星的周期、轨道平面、高度、线速度、角速度、绕行方向均是固定不变的,常用于无线电通信,故又称通信卫星。(只能在赤道的正上方)
(2)极地卫星运行时每圈都经过南北两极,由于地球自转,极地卫星可以实现全球覆盖。
(3)近地卫星是在地球表面附近绕地球做匀速圆周运动的卫星,其运行的轨道半径可近似认为等于地球的半径,其运行线速度约为7.9 km/s。
(4)赤道上的物体随地球自转而做匀速圆周运动,由万有引力和地面支持力的合力充当向心力。
它的运动规律不同于卫星,但它的周期、角速度与同步卫星相等,就是地球自转的周期、加速度。
近地卫星、同步卫星:F万=F心;赤道物体:F万-F支=F心 (F心≠F万);
①近地卫星与同步卫星(都是卫星)
高轨低速长周期 r同>r近;a、v、ω :近地卫星>同步卫星;T:近<同;
② 同步卫星与赤道上物体(周期相同)
同轴转动模型r同>r赤; T同=T物=24h(ω同); a、v:同步卫星>赤道物体
③ 近地卫星与赤道物体(半径相同)
T近
④三类物体匀速圆周运动的比较:
r同>r近=r物; T近
a近>a同>a物;F心近>F心同>F心物;F万物=F万近>F万同(质量相同)
4、近地卫星、同步卫星及赤道上物体的运行问题
课后作业-4
练习、(多选)如图所示,A为地面上的待发射卫星,B为近地圆轨道卫星,C为地球同步卫星。三颗卫星的线速度大小分别为vA、vB、vC,角速度大小分别为ωA、ωB、ωC,周期分别为TA、TB、TC,向心加速度大小分别为aA、aB、aC,则( )
A.TA=TC>TB B.ωA=ωC>ωB
C.vA>vB>vC D.aB>aC>aA
AD
练习、(多选)地球同步卫星到地心距离为r,运行速度为v1,加速度为a1;地球赤道上的物体随地球自转的加速度为a2,第一宇宙速度为v2,地球半径为R,则下列式子中正确的是( )
AC
五、卫星的变轨问题
解决变轨问题的基本思路:
假设轨道不变,分析由于速度的变化,此时受到的万有引力大小、向心力大小
五、卫星的变轨问题
假设卫星仍在原来轨道,分析由于速度变化,此时提供的向心力(万有引力)与需要的向心力大小关系,进而判断轨道的变化情况。
(1)提供<需要,离心运动,由小轨道变向大轨道
(2)提供>需要,近心运动,由大轨道变向小轨道
F提供=F需要,做圆周运动
F提供<F需要,做离心运动
F提供>F需要,做近心运动
1、基本思路:
1
2
3
P
Q
1 是圆轨道,2 是椭圆轨道,3 是圆轨道
O
1 轨道的Q点,点火加速,到达 2 轨道;
2 轨道的P点,再点火加速,到达 3 轨道;
2 椭圆轨道:
1、3 圆轨道:
综上:
变轨点
变轨点
开普勒第二定律
比较速度关系
离心运动:
五、卫星的变轨问题
1
2
3
P
Q
O
变轨点
变轨点
开普勒第三定律:
比较周期关系
椭圆轨道:
圆轨道:
(比较半径)
(比较半长轴)
综上:
1 是圆轨道,2 是椭圆轨道,3 是圆轨道
五、卫星的变轨问题
1
2
3
P
Q
O
变轨点
变轨点
比较加速度关系
1、3 圆轨道:
1、2 轨道的Q为同一个点:
2、3 轨道的P为同一个点:
综上:
1 是圆轨道,2 是椭圆轨道,3 是圆轨道
五、卫星的变轨问题
⑴判断卫星在不同圆轨道的运行速度大小时,
可根据“越远(高)越慢”的规律判断;
⑵判断卫星在同一椭圆轨道上不同点的速度大小时,可根据开普勒第二定律判断,即离中心天体越远,速度越小;
⑶判断卫星为实现变轨在某点需要加速还是减速时,可根据离心运动或近心运动的条件进行分析;(相切点,速度内小外大)
⑷判断卫星的加速度大小时,可根据 判断.
归纳:判断卫星变轨时速度、加速度、周期变化情况
⑸卫星不同轨道上运行周期的比较由开普勒第三定律判断
练习、(多选)如图所示,若关闭动力的航天飞机在月球引力作用下向月球靠近,并将与空间站在B处对接,已知空间站绕月球做匀速圆周运动的轨道半径为r,周期为T,万有引力常量为G,下列说法中正确的是( )
A. 图中航天飞机正加速飞向B处
B. 航天飞机在B处由椭圆轨道进入
空间站轨道时必须点火减速
C. 根据题中条件可以算出月球质量
D. 根据题中条件可以算出空间站受到月球引力的大小
ABC
练习、(多选)如图所示,卫星a距地球表面的距离为R,卫星b为地球同步卫星,两者都可视为绕地球沿同一方向做匀速圆周运动,某时刻卫星a、b恰好相距最近。已知地球质量为M、半径为R,地球自转的角速度为ω,引力常量为G,则下列说法正确的是( )
A.卫星b的速度小于卫星a的速度B.卫星a、b的发射速度都等于7.9km/s
D.卫星a和卫星b下一次相距最近还需经过
C.卫星b距地球表面的高度为
ACD
六、拉格朗日点
在两个大物体的引力场空间中存在着一些点。在这些点处的小物体可相对于两个大物体基本保持静止,这些点称为拉格朗日点。(与M2以相同周期绕M1运动)
这些点的存在由瑞士数学家欧拉于1767年推算出前三个,法国数学家拉格朗日于1772年推导证明剩下两个。
在每个由两大天体构成的系统中,按推论有5个拉格朗日点,但只有两个是稳定的(图中L4、L5),即小物体在该点处即使受外界引力的摄扰,仍然有保持在原来位置处的倾向。每个稳定点同两大物体所在的点构成一个等边三角形。
练习、(多选) 2018年5月25日,探月工程嫦娥四号任务“鹊桥”中继卫星成功实施近月制动,进入月球至地月拉格朗日L2点的转移轨道.当“鹊桥”位于拉格朗日点(如图中的L1、L2、L3、L4、L5所示,人们称为地月系统拉格朗日点)上时,会在月球与地球的共同引力作用下,几乎不消耗燃料而保持与月球同步绕地球做圆周运动,下列说法正确的是(月球的自转周期等于月球绕地球运动的周期)( )
A.“鹊桥”位于L2点时,“鹊桥”绕地球运动的周期
和月球的自转周期相等
B.“鹊桥”位于L2点时,“鹊桥”绕地球运动的
向心加速度大于月球绕地球运动的向心加速度
C.L3和L2到地球中心的距离相等
D.“鹊桥”在L2点所受月球和地球引力的合力比在其余四个点都要大
ABD
练习、(多选)拉格朗日点是小天体在两个大天体的引力作用下基本能保持相对静止的点。如图是日地系统的5个拉格朗日点(L1、L2、L3、L4、L5),设想未来人类在这五个点上都建立了太空站。若不考虑其他天体对太空站的引力,下列说法正确的是( )
BC
A.位于L1点的太空站受力平衡B.位于L2点的太空站的线速度大小大于地球的
线速度大小C.位于L3点的太空站的向心加速度大小大于位于
L1点的太空站的向心加速度大小D.位于L4点的太空站受到的向心力大小等于位于L5点的太空站受到的向心力大小
练习、(2019·河北唐山市第一次模拟)2018年6月14日,我国探月工程嫦娥四号的中继星“鹊桥”顺利进入地月拉格朗日L2点的运行轨道,为地月信息联通搭建“天桥”.如图所示,L2点位于地球与月球中心连线的延长线上,“鹊桥 ”位于该点,在几乎不消耗燃料的情况下与月球同步绕地球做圆周运动,已知地球、月球和“鹊桥”的质量分别为M1、M2、m,地球和月球球心间的距离为R,L2点到月球中心的距离为x,则x满足( )
C
嫦娥奔月
敦煌飞天
六、载人航天与太空探索
14世纪末,明朝的士大夫万户把47枚火箭绑在自己坐的椅子上,两只手各拿一个大风筝。然后叫他的仆人同时点燃所有的火箭,想借火箭的推力飞上月球,然后利用风筝平稳着路,不幸火箭爆炸,万户也为此献出了生命。
六、载人航天与太空探索
康斯坦丁·齐奥尔科夫斯基
(1857-1935前苏联)
“地球是人类的摇篮,但人类不会永远呆在摇篮里。”
多级火箭理论
六、载人航天与太空探索
1961 年 4 月 12 日,苏联航天员加加林进入了东方一号载人飞船。火箭点火起飞,飞船绕地球飞行一圈,历时108 min,然后重返大气层,安全降落在地面,铸就了人类首次进入太空的丰碑。
1969 年 7 月 16 日 9 时 32 分,运载阿波罗 11 号飞船的土星 5 号火箭在美国卡纳维拉尔角点火升空,拉开人类登月这一伟大历史事件的帷幕。7 月 20 日下午 10 时 56 分,指挥长阿姆斯特朗小心翼翼地踏上月面,并说出了那句载入史册的名言 :“对个人来说,这不过是小小的一步,但对人类而言,却是巨大的飞跃。”
六、载人航天与太空探索
钱学森,世界著名科学家,空
气动力学家,中国载人航天奠基人,
“中国科制之父”和“火箭之王”,
由于钱学森回国效力,中国导弹、
原子弹的发射向前推进了至少20年。
曾任美国麻省理工学院和加州理
工学院教授。1950年钱学森回国受
阻,并受美国方面监禁,1955年,
在毛泽东主席和周恩来总理的争取下回到中国。
中国航天之父
中国航天之父:钱学森(1911.12.11-2009.10.31)
六、载人航天与太空探索
2003年10月15日9时,神州五号宇宙飞船在酒泉卫星发射中心成功发射,把中国第一位航天员杨利伟送入太空。
六、载人航天与太空探索
人类一直有“飞天”的梦想,万有引力定律的发现,不仅破解了天上行星的运行规律,也为人类开辟了上天的 理论之路。随着技术的进步,人类迈向太空的脚步越来越 大,越来越坚实。
六、载人航天与太空探索
1957.10.4:第一颗人造卫星(苏联)
1961.4.12:第一次载人飞船(苏联,加加林)
1969.7.16-7.20:第一次登月(美国,阿姆斯特朗)
1970.4.24:中国第一颗人造卫星(东方红一号)
神舟计划:建设自己的空间站
2003.10.15:神舟五号载人飞船(中国,杨利伟)
2021.10.16:神舟十三号载人飞船(翟志刚,王亚平,叶光富,将在太空工作生活六个月)
嫦娥计划:2004年中国开展探月工程
2007.10.24:发射嫦娥一号
2020.11.24:发射嫦娥五号,目前已取样返回
火星计划:2016年立项,开展探测火星工程
2020.7.23:天问一号发射
2021.2.10:被火星捕获
2021.5.15:着陆
2021.5.22:祝融号火星车驶离着陆平台踏上火星表面巡视探测
四.梦想成真
载人航天与太空探索
对地球:v1=7.9km/s (环绕速度)
7.9km/s
c.当v ≥16.7km/s时,脱离太阳,第三宇宙速度也称逃逸速度
课堂小结:
a.第一宇宙速度:
(对任何天体都适用)
一、宇宙速度(卫星发射)
二、 卫星运行的规律————卫星环绕(卫星运行)
基本思路;1、卫星绕地球做匀速圆周运动,万有引力提供向心力(F提供=F需要)
2、万有引力等于重力
三、同步卫星
1、同步卫星与地面相对静止,与地球自转同步,周期为24h。
2、同步卫星运行方向与地球自转的方向相同。
3、同步卫星定点在赤道上方,离地的高度、运行的速率是唯一确定的。
四、卫星变轨
基本思路:先假设卫星在原来的轨道上,分析此时提供的向心力;运动需要的向心力。如果提供大于需要——近心运动(r变小);提供小于需要——离心运动(r变大)
