苏科版八年级数学下册 9.5 三角形的中位线 学案(无答案)
文档属性
| 名称 | 苏科版八年级数学下册 9.5 三角形的中位线 学案(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 96.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 06:56:30 | ||
图片预览


文档简介
9.5三角形的中位线(2)
学习目标: 1、掌握三角形的中位线的概念、性质;
会利用三角形中位线的性质解决四边形各边中点的图形性质;
学习重点难点:从三角形中位线性质的探索过程中抽象出四边形各边中点的图形性质;
学习过程:
一、复习回顾:
1、已知△ABC的3条中位线分别为3cm,4cm、6cm,则△ABC的周长为 cm.
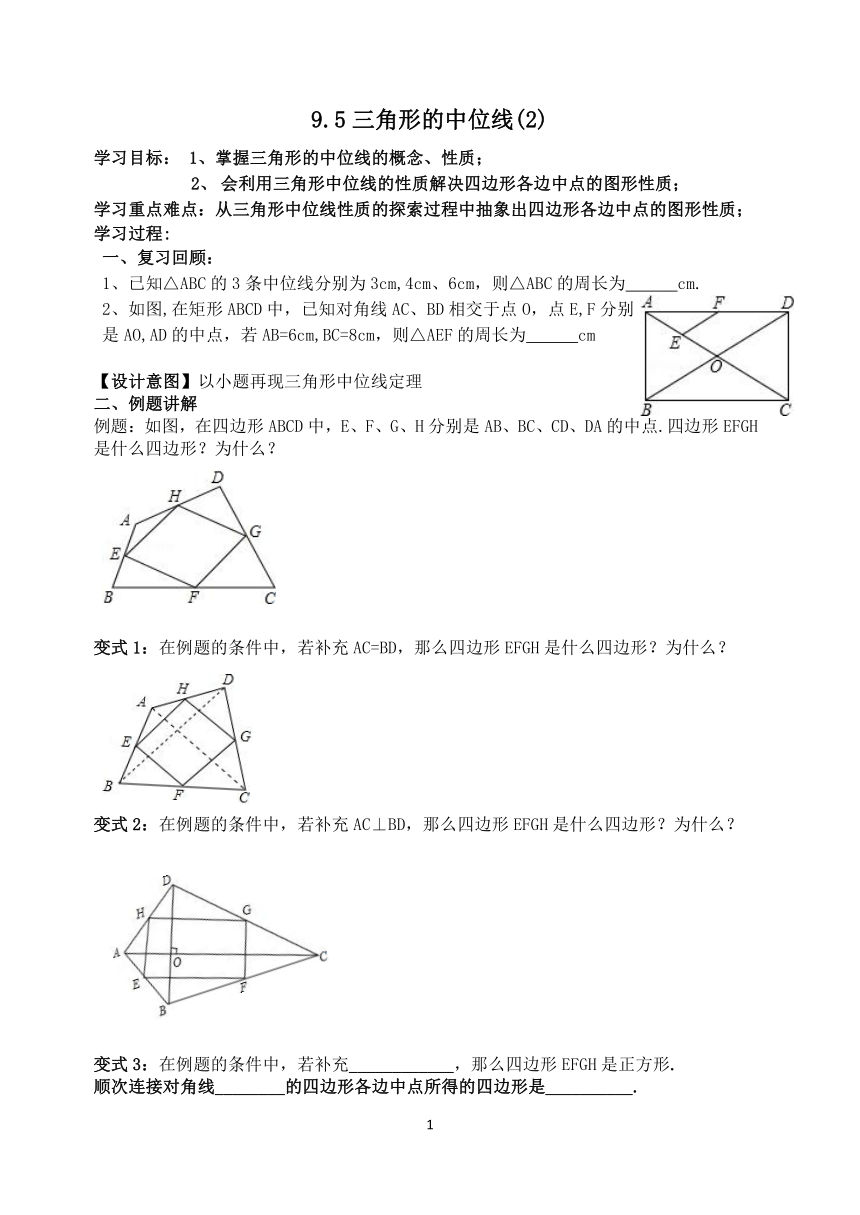
2、如图,在矩形ABCD中,已知对角线AC、BD相交于点O,点E,F分别
是AO,AD的中点,若AB=6cm,BC=8cm,则△AEF的周长为 cm
【设计意图】以小题再现三角形中位线定理
二、例题讲解
例题:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.四边形EFGH是什么四边形?为什么?
变式1:在例题的条件中,若补充AC=BD,那么四边形EFGH是什么四边形?为什么?
变式2:在例题的条件中,若补充AC⊥BD,那么四边形EFGH是什么四边形?为什么?
变式3:在例题的条件中,若补充____________,那么四边形EFGH是正方形.
顺次连接对角线________的四边形各边中点所得的四边形是__________.
顺次连接对角线________的四边形各边中点所得的四边形是__________.
顺次连接对角线________的四边形各边中点所得的四边形是__________.
【设计意图】
通过这一例题及其变式,让学生在解决问题的过程中,学会把四边形的问题转化成三角形,会熟练运用三角形中位线定理,并回顾了特殊四边形的判定方法,最后自己能总结出中点四边形与原四边形的对角线的关系.在这过程中,学生自己运用知识解决问题的能力得到了锻炼和提升.
变式4:在上述四边形ABCD中,若AC⊥BD,AC=a,BD=b,顺次连接四边形各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1的中点,得到四边形A2B2C2D2……如此进行下去,得到四边形AnBn nDn,
问(1)四边形A2B2C2D2是______形,面积是________(2)四边形A3B3C3D3是______形,面积是_______ (3)四边形AnBn nDn的面积是 _______
【设计意图】
通过这一题的训练,让学生对中点四边形的形状的判断更为熟练,并会解决一些规律问题,是对优秀学生的能力的提升.
三、灵活运用
类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,请看下面的案例.如图1,点P是线段AB的中点,分别以AP和BP为边在线段AB的同侧作等边三角形APC和等边三角形BPD,连接AD和BC,则四边形ABDC的中点四边形一定是________.如图2,若P是线段AB上任一点,在AB的同侧作△APC和△BPD,使PC=PA,PD=PB,∠APC=∠BPD,连接CD,设点E,F,G,H分别是AC,AB,BD,CD的中点,顺次连接E,F,G,H.请你接着往下解决三个问题:
(1)猜想四边形ABCD的中点四边形EFGH的形状 ________ (直接回答);
(2)当点P在线段AB的上方时,如图3,在△APB的外部作△APC和△BPD,其它条件不变,(1)中结论还成立吗?说明理由;
(3)如果(2)中,∠APC=∠BPD=90°,其它条件不变,先补全图4,再判断四边形EFGH的形状,并说明理由.
【设计意图】
数学学习不仅要教会学生知识,更要教会学生自己解决问题的方法,提高学生自主学习的能力,该题在前面的内容呈现后再做,就大大降低了难度,能让大部分学生解决,从而提高学生学习的自信,激发学习数学的动力和兴趣.
课堂小结
本节课你收获到了什么?
(
H
F
C
A
G
E
D
)课后作业
顺次连接任意四边形各边中点所得四边形是 ;
如图,当四边形ABCD中AC=BD时,四边形EFGH是_____________;
当AC⊥BD时,四边形EFGH是_____________;
当AC=BD且AC⊥BD时,四边形EFGH是_________.
如果顺次连接四边形各边中点所得的四边形是矩形,那么原来的四边形应具备的条件是( )
A. 有一个角是直角 B. 对角线相等 C.对角线互相垂直 D.对角线互相平分
4、如果四边形的对角线相等,那么顺次连结四边形中点所得的四边形是( )
A.矩形 B.菱形 C.正方形 D.以上都不对
5、已知一矩形的周长是24cm,相邻两边之比是1:2,那么这个矩形的面积是 ( )
A.24cm2 B.32cm2 C.48cm2 D.128cm2
6、如图,过矩形ABCD的对角线BD上一点R分别作矩形两边的平行线MN与PQ,那么图中矩形AMRP的面积S1,与矩形QCNR的面积S2的大小关系是 ( )
A. S1> S2 B. S1= S2 C. S1< S2 D. 不能确定
7、如图,以三角形的一条中位线和第三边上的中线为对角线的四边形是( )
A.正方形 B.平行四边形 C.菱形 D.矩形
第 6题图 第 7题图 第 8题图
8、如图,点D,E,F分别是⊿ABC各边的中点,BH⊥AC,垂足为H,DE=6cm,则FH=_______.
9、如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=5cm,求EF的长.
10、如图,在四边形ABCD中,AB=CD,M,N,P,Q分别是AD,BC,BD,AC的中点.
猜想MN与PQ的关系,并说明理由.
11、如图,在平行四边形ABCD中,E、F分别是BC、AD的中点,AE与BF相交于点G,DE与CF相交于点H,试说明GH∥AD且GH=AD
1
学习目标: 1、掌握三角形的中位线的概念、性质;
会利用三角形中位线的性质解决四边形各边中点的图形性质;
学习重点难点:从三角形中位线性质的探索过程中抽象出四边形各边中点的图形性质;
学习过程:
一、复习回顾:
1、已知△ABC的3条中位线分别为3cm,4cm、6cm,则△ABC的周长为 cm.
2、如图,在矩形ABCD中,已知对角线AC、BD相交于点O,点E,F分别
是AO,AD的中点,若AB=6cm,BC=8cm,则△AEF的周长为 cm
【设计意图】以小题再现三角形中位线定理
二、例题讲解
例题:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.四边形EFGH是什么四边形?为什么?
变式1:在例题的条件中,若补充AC=BD,那么四边形EFGH是什么四边形?为什么?
变式2:在例题的条件中,若补充AC⊥BD,那么四边形EFGH是什么四边形?为什么?
变式3:在例题的条件中,若补充____________,那么四边形EFGH是正方形.
顺次连接对角线________的四边形各边中点所得的四边形是__________.
顺次连接对角线________的四边形各边中点所得的四边形是__________.
顺次连接对角线________的四边形各边中点所得的四边形是__________.
【设计意图】
通过这一例题及其变式,让学生在解决问题的过程中,学会把四边形的问题转化成三角形,会熟练运用三角形中位线定理,并回顾了特殊四边形的判定方法,最后自己能总结出中点四边形与原四边形的对角线的关系.在这过程中,学生自己运用知识解决问题的能力得到了锻炼和提升.
变式4:在上述四边形ABCD中,若AC⊥BD,AC=a,BD=b,顺次连接四边形各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1的中点,得到四边形A2B2C2D2……如此进行下去,得到四边形AnBn nDn,
问(1)四边形A2B2C2D2是______形,面积是________(2)四边形A3B3C3D3是______形,面积是_______ (3)四边形AnBn nDn的面积是 _______
【设计意图】
通过这一题的训练,让学生对中点四边形的形状的判断更为熟练,并会解决一些规律问题,是对优秀学生的能力的提升.
三、灵活运用
类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,请看下面的案例.如图1,点P是线段AB的中点,分别以AP和BP为边在线段AB的同侧作等边三角形APC和等边三角形BPD,连接AD和BC,则四边形ABDC的中点四边形一定是________.如图2,若P是线段AB上任一点,在AB的同侧作△APC和△BPD,使PC=PA,PD=PB,∠APC=∠BPD,连接CD,设点E,F,G,H分别是AC,AB,BD,CD的中点,顺次连接E,F,G,H.请你接着往下解决三个问题:
(1)猜想四边形ABCD的中点四边形EFGH的形状 ________ (直接回答);
(2)当点P在线段AB的上方时,如图3,在△APB的外部作△APC和△BPD,其它条件不变,(1)中结论还成立吗?说明理由;
(3)如果(2)中,∠APC=∠BPD=90°,其它条件不变,先补全图4,再判断四边形EFGH的形状,并说明理由.
【设计意图】
数学学习不仅要教会学生知识,更要教会学生自己解决问题的方法,提高学生自主学习的能力,该题在前面的内容呈现后再做,就大大降低了难度,能让大部分学生解决,从而提高学生学习的自信,激发学习数学的动力和兴趣.
课堂小结
本节课你收获到了什么?
(
H
F
C
A
G
E
D
)课后作业
顺次连接任意四边形各边中点所得四边形是 ;
如图,当四边形ABCD中AC=BD时,四边形EFGH是_____________;
当AC⊥BD时,四边形EFGH是_____________;
当AC=BD且AC⊥BD时,四边形EFGH是_________.
如果顺次连接四边形各边中点所得的四边形是矩形,那么原来的四边形应具备的条件是( )
A. 有一个角是直角 B. 对角线相等 C.对角线互相垂直 D.对角线互相平分
4、如果四边形的对角线相等,那么顺次连结四边形中点所得的四边形是( )
A.矩形 B.菱形 C.正方形 D.以上都不对
5、已知一矩形的周长是24cm,相邻两边之比是1:2,那么这个矩形的面积是 ( )
A.24cm2 B.32cm2 C.48cm2 D.128cm2
6、如图,过矩形ABCD的对角线BD上一点R分别作矩形两边的平行线MN与PQ,那么图中矩形AMRP的面积S1,与矩形QCNR的面积S2的大小关系是 ( )
A. S1> S2 B. S1= S2 C. S1< S2 D. 不能确定
7、如图,以三角形的一条中位线和第三边上的中线为对角线的四边形是( )
A.正方形 B.平行四边形 C.菱形 D.矩形
第 6题图 第 7题图 第 8题图
8、如图,点D,E,F分别是⊿ABC各边的中点,BH⊥AC,垂足为H,DE=6cm,则FH=_______.
9、如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=5cm,求EF的长.
10、如图,在四边形ABCD中,AB=CD,M,N,P,Q分别是AD,BC,BD,AC的中点.
猜想MN与PQ的关系,并说明理由.
11、如图,在平行四边形ABCD中,E、F分别是BC、AD的中点,AE与BF相交于点G,DE与CF相交于点H,试说明GH∥AD且GH=AD
1
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
