3.3 离心现象 教案

第三章　圆周运动
第3节　离心现象
本节是圆周运动的应用课，内容丰富。教材中的每个例子的选择都各有特点，很有代表性：铁路的弯道时分析水平面上的匀速圆周运动；拱形桥和凹形桥是分析竖直面上的非匀速圆周运动；航天器中的失重现象研究失重问题；离心运动则研究向心力不足时物体的运动趋势。讨论教材中的这几个实例，要抓住先分析物体所受的力，然后列出方程，解方程。
【物理观念】知道离心现象的产生及离心运动的应用，会分析水平和竖直面内的匀速圆周运动问题。
【科学思维】能分析小球通过竖直圆环最高点和最高点时的向心力，知道小球能通过最高点的条件。
【科学探究】会通过实例分析离心运动的条件，以及离心运动在生产生活中的应用。
【科学态度与责任】认识到生活中的物理问题可以用所学知识解决，科学与生活紧密联系，且对社会的发展有很深的影响。
【教学重点】离心现象产生的原因以及离心运动的应用。
【教学难点】向心力的实例分析。
【导入新课】
思考：为什么在拐弯处容易发生事故？
应该如何避免这种事件的发生？
【新课讲授】
车辆转弯时所需的向心力
1、汽车转弯
思考：汽车在水平地面上转弯时是什么力提供向心力的呢
汽车在水平路面上转弯所需要的向心力来源:汽车侧向所受的静摩擦力。
当汽车转弯的半径一定时,汽车的速度v越大,所需的向心力也越大,静摩擦力也越大，汽车做圆周运动。---------------供=需，汽车做匀速圆周运动。
当所需要的向心力大于所提供的向心力（即最大静摩擦力）时，汽车将发生侧滑现象。---------供〈需，汽车发生侧滑。
【赛道的设计】
2、火车转弯
思考：火车转弯时是在做圆周运动，什么力提供向心力？
（1）内外轨道一样高
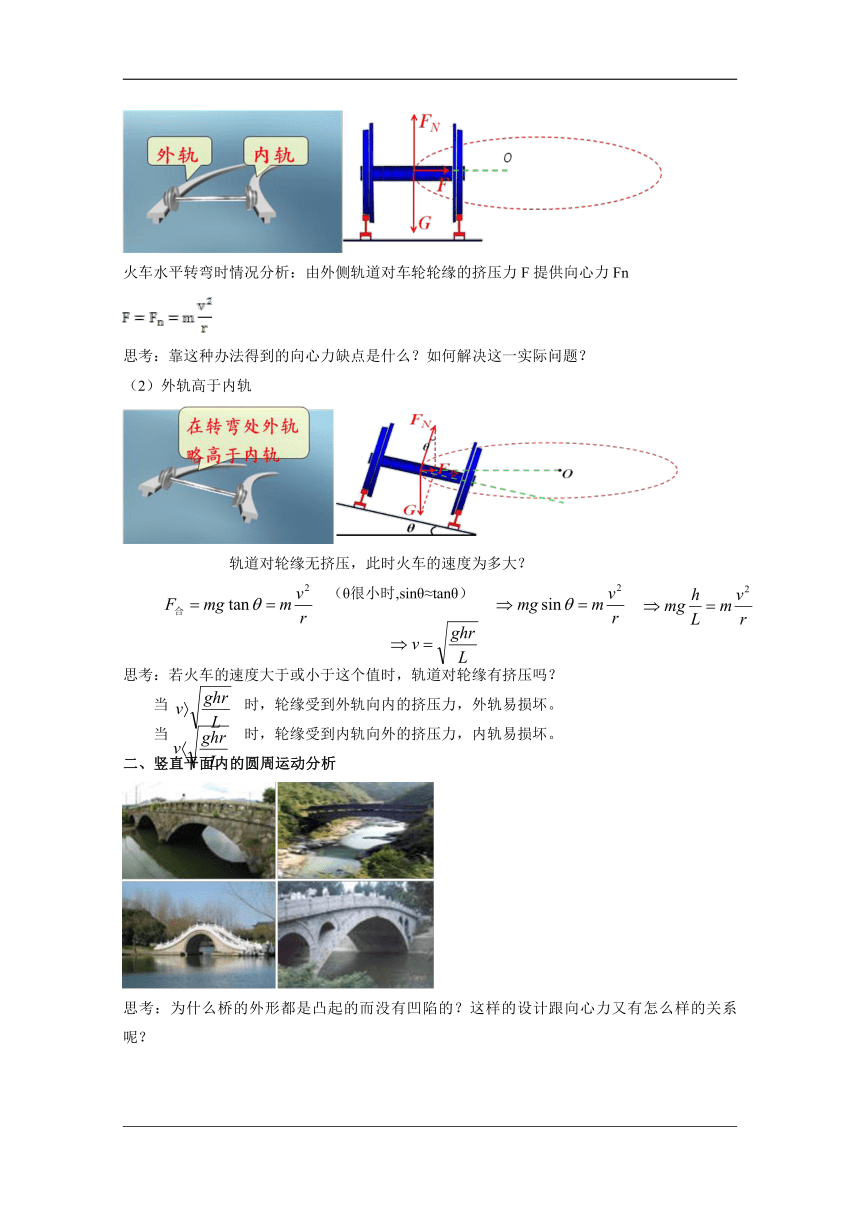
火车水平转弯时情况分析：由外侧轨道对车轮轮缘的挤压力F提供向心力Fn
思考：靠这种办法得到的向心力缺点是什么？如何解决这一实际问题？
（2）外轨高于内轨
轨道对轮缘无挤压，此时火车的速度为多大？
（θ很小时,sinθ≈tanθ）
思考：若火车的速度大于或小于这个值时，轨道对轮缘有挤压吗？
当 时，轮缘受到外轨向内的挤压力，外轨易损坏。
当 时，轮缘受到内轨向外的挤压力，内轨易损坏。
二、竖直平面内的圆周运动分析
思考：为什么桥的外形都是凸起的而没有凹陷的？这样的设计跟向心力又有怎么样的关系呢？
1.求汽车以速度v过半径为r 的拱桥最高点时对拱桥的压力？
【解】G和FN的合力提供汽车做圆周运动的向心力，由牛顿第二定律得：
（FN ＜mg，失重状态 ）
可见汽车的速度越大对桥的压力越小。
当时汽车对桥的压力为零。（临界速度）
思考：当ｖ大于ｖ临界时，汽车做什么运动？----------汽车脱离桥面，做平抛运动。
2.求汽车过凹形路段最低点时对路面的压力？
【解】G和FN的合力提供汽车做圆周运动的向心力，由牛顿第二定律得：
(超重状态)
可见汽车的速度V越大，对桥的压力越大。
思考：若汽车通过凹桥的速度增大，会出现什么情况？（速度越大，压力越大，可能会爆胎）
思考:过山车为什么在最高点也不会掉下来
绳和内轨模型
物做近心运动
小结：轨道提供支持力,绳子提供拉力。
② 杆儿和双轨模型
能过最高点的临界条件:
当速度v > 时, 杆对小球是拉力;
当速度v < 时, 杆对小球是支持力;
当速度v = 时, 杆对小球无作用力。 FN=0
小结：杆既可以提供拉力,也可以提供支持力。
三、生活中的离心运动
向心力的“供求”关系——所需向心力与提供向心力；
F合 = mω2r， 物体做匀速圆周运动
思考：如果所需向心力与提供向心力大小不相等时物体将如何运动？
1、定义：做匀速圆周运动的物体，在所受合力突然消失，或者不足以提供圆周运动所需的向心力时，做逐渐远离圆心的运动，这种运动叫做离心运动。
2、条件：0 ≤F合＜mω2r 供〈需
3、离心现象的应用：
离心甩干 离心抛掷 离心脱水 离心分离
4、离心运动的防止
在水平公路上行驶的汽车，转弯时所需的向心力是由车轮与路面的静摩擦力提供的。如果转弯时速度过大，所需向心力Fn大于最大静摩擦力Fmax （Fmax不足以提供向心力），汽车将做离心运动而造成交通事故.因此，在公路弯道处，车辆行驶不允许超过规定的速度。
高速转动的砂轮、飞轮等，都不得超过允许的最大转速。转速过高时，砂轮、飞轮内部分子间的相互作用力不足以提供所需向心力，离心运动会使它们破裂，酿成事故。
四、课堂小结
一.车辆转弯时所需的向心力
1. 向心力的来源:外轨高于内轨时,重力与支持力的合力是使火车转弯的向心力
2转弯处的半径和火车运行速度的条件限制.
二.竖直平面内的圆周运动分析
汽车过拱形桥时,对桥面的压力与重力比较
三.生活中的离心运动
1.离心现象的分析与讨论．
2.离心运动的应用和防止．
PAGE