六年级数学下册课件-7.2.7立体图形的表面积和体积苏教版(共88张ppt)
文档属性
| 名称 | 六年级数学下册课件-7.2.7立体图形的表面积和体积苏教版(共88张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 11:54:22 | ||
图片预览





文档简介
(共88张PPT)
立体图形的复习
这是我们学过的立体图形,
如果把它们分为两类,可以怎么样分呢?
名称 顶点 棱 面 体
长方体
8个
12条
(分为4组,以相交于同一顶点的三条棱为一组)
(分为3组,有4长、4宽、4高)
L=4a+4b+4h
L=4(a+b+h)
L=12a
6个
(相对的面完全相同)
(有两个相对的面是正方形,其余四个都是完全相同的长方形)
S表=(ab+ah+bh) ×2
(六个面完全相同)
S表=2a +4ab
S表=6a
V=S底h
=abh
V=S底h
=a
(a,a,a)
正方体
(a,b,h)
(a,a,h)
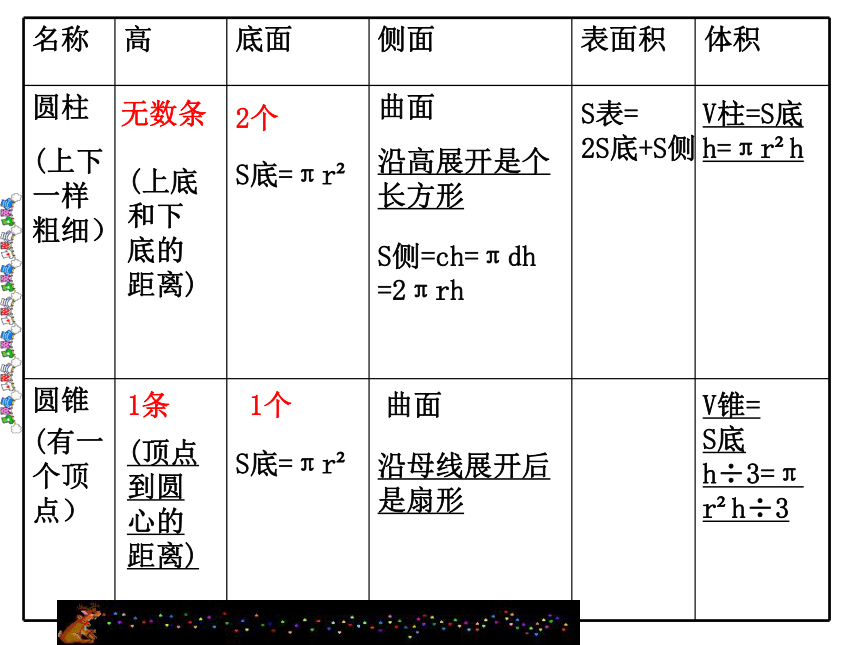
名称 高 底面 侧面 表面积 体积
圆柱
圆锥
(上下一样粗细)
无数条
(上底和下底的距离)
(有一个顶点)
2个
1个
1条
(顶点到圆心的距离)
曲面
S底=πr
S底=πr
曲面
V锥=
S底h÷3=πr h÷3
S侧=ch=πdh
=2πrh
S表=
2S底+S侧
沿高展开是个长方形
沿母线展开后是扇形
V柱=S底h=πr h
V=
V=
V=
V=
abh
a
3
πr h
1
3
πr h
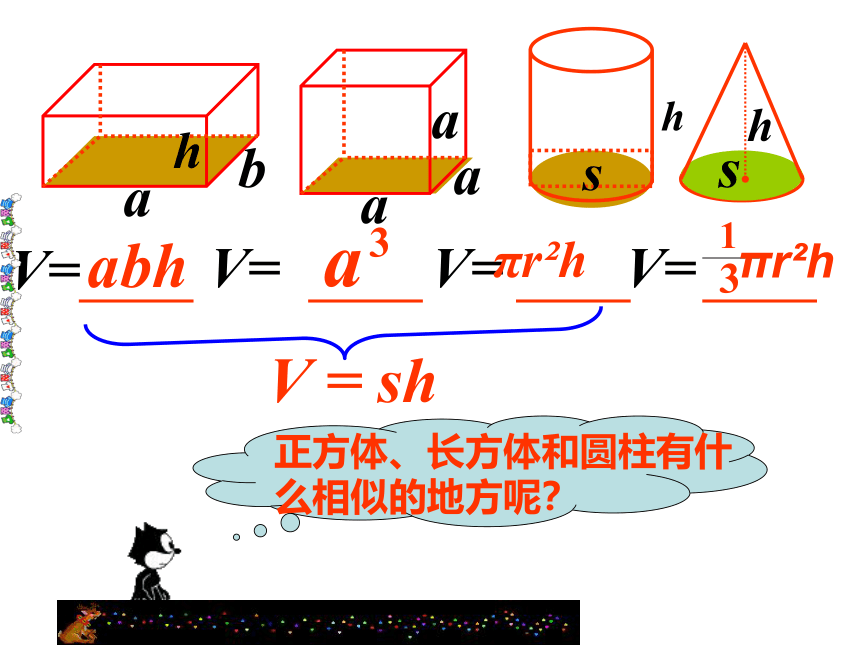
V = sh
正方体、长方体和圆柱有什么相似的地方呢?
h
a
b
a
a
a
s
h
s
h
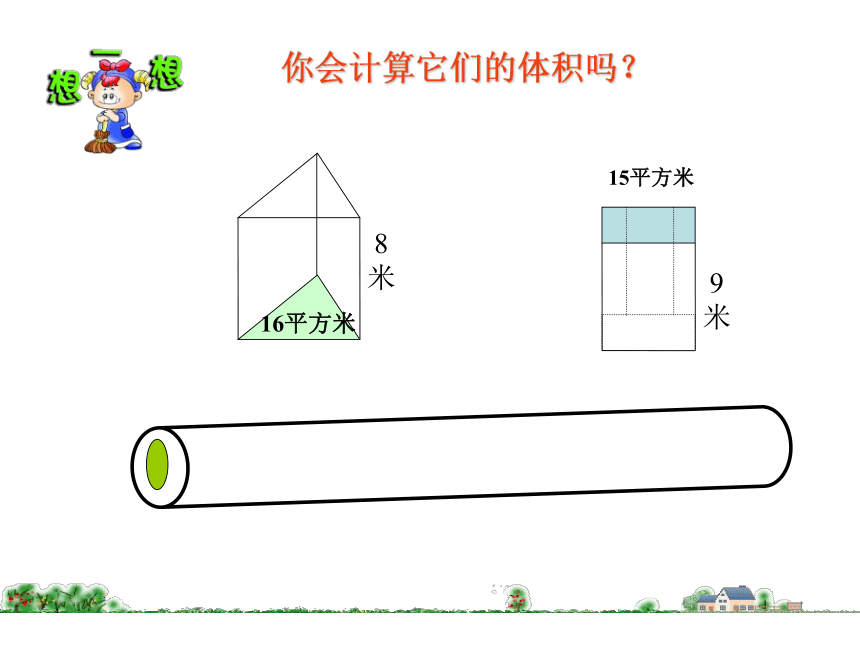
16平方米
8
米
9
米
15平方米
你会计算它们的体积吗?
立体图形
生活中变式题型
生活中基本题型
基本概念
体积
面积
棱
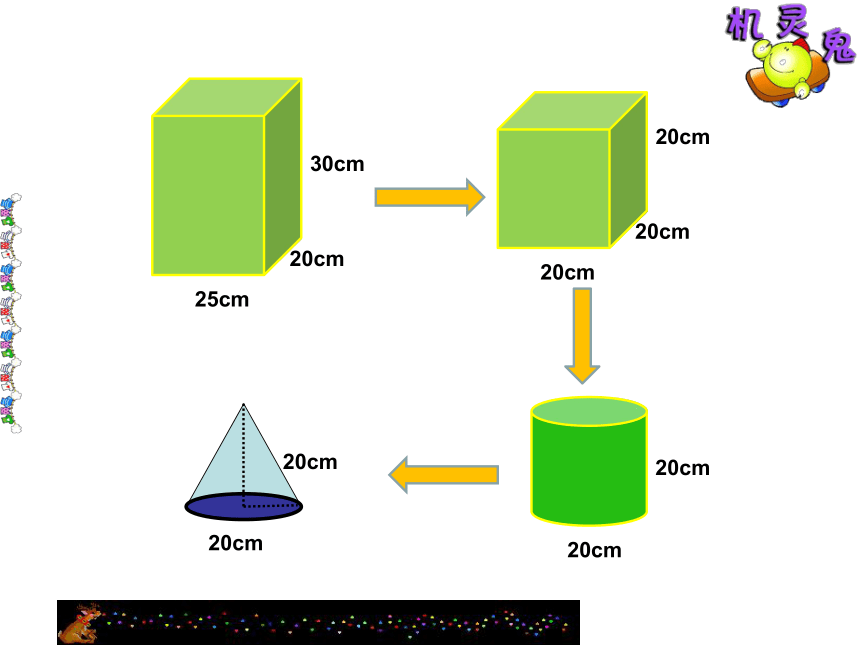
25cm
20cm
30cm
20cm
20cm
20cm
20cm
20cm
20cm
20cm
立体图形
生活中变式题型
生活中基本题型
基本概念
体积
面积
棱
体积变化
表面变化
棱
综合运用
1.将一个棱长25cm的正方体框架改成长方体,已知长方体长25cm,宽20cm,求高是多少厘米?
25×12 ÷ 4-25-20=30(cm)
答:长方体高是30cm。
2.用十字捆扎法将下面蛋糕进行捆扎,接头
处25cm,求绳子的长度。
25cm
20cm
30cm
d=25cm
30cm
25 ×2 +20 ×2 +30 ×4
+ 25=235(cm)
答:绳长235cm。
25 ×4 +30 ×4 + 25=245(cm)
答:绳长245cm。
3.(1)把长方体的高减少2cm,就变成了一个正方体,
已知表面积减少56cm ,求原来长方体的体积。
2cm
28cm
56 ÷2 =28(cm)
7 +2 =9(cm)
7 × 7 × 9=441(cm )
答:原来长方体体积441cm 。
(2)把圆柱的高减少2cm,表面积就减少25.12cm ,已知原来圆柱的高为9cm,求原来长方体的体积。
2cm
12.56cm
7cm
25.12 ÷2 =12.56(cm)
12.56 ÷ 3.14 ÷ 2 =2(cm)
2 π ×9 =36π(cm )
答:原来圆柱的体积是36πcm 。
28÷4 =7(cm)
4.(1)已知长方体的横截面为12cm ,沿横截面将其
分成若干个小长方体(如图),表面积增加多少平方厘米?
12 ×2 =24(cm )
3 - 1 = 2(次)
2 ×2 =4(个)
12 ×2 =24(cm )
(n - 1) × 2×12
n个
一刀两断
4.(2)已知圆柱的横截面为12cm ,沿横截面将其分成
若干个小圆柱(如图),表面积增加多少平方厘米?
n个
一刀两断
12 ×2 =24(cm )
3 - 1 = 2(次)
2 ×2 =4(个)
12 ×2 =24(cm )
(n - 1) × 2×12
4.(3)已知圆柱的底面直径是6cm,高是8cm,沿轴线将
其分成两个相等的半圆柱,表面积增加多少平方厘米?
6cm
8cm
6 ×8 × 2=96(cm )
答:表面积增加了96cm 。
5.把一个圆柱切成若干等分,拼成一个近似的长方体,已知圆柱的半径和高均为10cm。那么长方体的表面积比圆柱增加了多少平方厘米
10 × 10 ×2 =200cm
10
厘
米
6.长方体的长15cm,宽10cm,高8cm,将两个这样的长方体
叠放在一起,组成的新长方体的表面积可能是多少平方厘米?
(30,10,8)
(30 × 10 +30 ×8 + 10×8) × 2=1240(cm )
(15,20,8)
(15 × 20 +15×8 + 20×8) × 2=1160(cm )
(15,10,16)
(15 × 10 +15×16 + 10×16) × 2=1100(cm )
7.将8个正方体熔铸成和它等底等高的圆柱,可以熔铸
几个?如果熔铸成圆锥呢?
正方体
圆柱
8个
8个
1 :1
圆锥
24个
1 :3
8.一个圆锥形状的沙堆,底面周长是31.4米,高1.5米。将这堆沙铺成宽2m、高0.1m的长方体,可以铺多长?
3.14×52×1.5×
=3.14×12.5
=39.25(立方米)
314÷3.14÷2=5(米)
39.25÷2÷0.1=196.25(米)
答:可以铺196.25米。
9.测量不规则的物体可以采用转化的策略。圆柱的半径是5cm,高是10cm,将其盛满水,放入一块石子,然后将石子取出,水面下降了4cm,求石子的体积。
5 π×4=100π(cm )
答:石子的体积是100πcm 。
10.圆柱里有一半水,将其倒入与它等底等高的圆锥中,还剩10L水,那么,你知道圆柱的容积吗?
1
10 ÷( - )=60(L)
1
3
1
2
答:圆柱的容积是60L。
11.把一个圆柱切成若干等分,拼成一个近似的长方体。圆柱的侧面积是72平方米,底面半径是3米。求圆柱的体积是多少?
72÷2×3
圆柱的体积=侧面积÷2×半径
底面积
× 高
12.一个用塑料薄膜覆盖的草莓大棚,长15米,横截面是一个半径2米的半圆。
①大棚内的空间有多少大?
22×π×15÷2
=3.14×4×15÷2
=3.14×30
=94.2(立方米)
12.一个用塑料薄膜覆盖的蔬菜大棚,长15米,横截面是一个半径2米的半圆。
②覆盖在这个大棚上的塑料薄膜约有多少平方米?
3.14×22+3.14×22×15÷2
=3.14×(4+30)
=3.14×34
=106.76(平方米)
谢 谢 指 导 !
底面
侧面
底面
高
底面
侧面
高
立体图形
生活中变式题型
生活中基本题型
基本概念
说说下列各图是由哪些基本图形组成的。
长方体的表面积= (上 面 + 前 面 + 侧 面 )×2
=(长×宽+长×高+宽×高)×2
S=(ab+ah+bh)×2
下面
前面
后面
左面
右面
上面
棱长1厘米的正方体,体积是1立方厘米
长5厘米
宽4厘米
高3厘米
长方体的体积正好等于它的长、宽、高的乘积。
长方体的体积=长×宽×高
V=abh
正方体的表面积=一个面的面积×6
S=a2 × 6
棱长4厘米
棱长4厘米
棱长4厘米
因为正方体是长、宽、高都相等的长方体,所以
正方体的体积=棱长×棱长×棱长
V=
·
a
a
a
·
V=
3
a
或
底面周长
高
底面
底面
侧面
S侧=ch=πdh=2πrh
底面积
高
怎样求圆柱的体积呢?
圆柱体积的大小与哪些条件有关?
因为长方体的体积=底面积×高
所以圆柱的体积=底面积×高
V = S h
底面
h
h
r
r
πr
V= πr × h
2
V长方体 = V圆柱
= πr × h
2
V=abh
V=Sh
= πr ×r × h
圆柱体积=底面积 高
1
3
圆锥体积=
底面积 高
底面
侧面
底面
曲面
扇形
名称 高 底面 侧面 表面积 体积
圆柱
(上下一样粗细) 无数条
(上底和下底的距离) 2个
S底=πr 曲面
沿高展开是个长方形
S侧=ch=πdh
=2πrh
S表=
2S底+S侧 V柱=S底h=πr h
圆锥
(有一个顶点) 1条
(顶点到圆心) 1个
S底=πr 曲面
沿母线展开后是扇形 V锥=
S底h=πr h
三、 判断(对的打“√ ”,错的打“× ”。)
3.下图中的正方体、圆柱和圆锥底
面积相等,高也相等。圆锥的体积是
正方体的 。 ( )
√
3
1
三、 判断(对的打“√ ”,错的打“× ”。)
1.一个圆柱形的水桶能装水15升,我们就说水桶的体积是15立方分米。
………………( )
×
三、判断(对的打“√ ”,错的打“× ”。)
2.一个长方体的长、宽、高分别是a米、b米、h米。如果高增加2米,体积比原来增加2ab立方米
……………… ( )
√
四、选择正确答案的序号填入括号里
1. 把一个圆柱的底面平均分成若干个扇形,然后切开拼成一个近似的长方体。下面哪句话是正确的?( )
A、表面积和体积都没变
B、表面积和体积都发生了变化
C、表面积变了,体积没变
D、表面积没变,体积变了
C
四、选择正确答案的序号填入括号里
A、 54 B、 18
C 、 0.6 D、 6
2. 等底等体积的圆柱和圆锥,圆锥的高是18厘米,那么圆柱的高是( )厘米。
D
四、选择正确答案的序号填入括号里
3. 等高等体积的圆柱和圆锥,圆柱的底面积是6平方厘米,那么圆锥的底面积是( )平方厘米。
A、6 B、18
C、2 D、36
B
四、选择正确答案的序号填入括号里
4.把一个底面半径是2分米、高是3分米的圆柱形容器中注满水,现垂直轻轻插入一根底面积是5平方分米,高是4分米的方钢,溢出水的体积是( )毫升。
A、20 B、15
C、20000 D、15000
D
五、生活中的数学问题
1.这个长方体的鱼池,长10米,宽6米,深是2米。
①这个这个鱼池的占地面积是多少平方米?
10×6=60(平方米)
五、生活中的数学问题
1.这个长方体的鱼池,长10米,宽6米,深是2米。
②在池内的侧面和池底铺上瓷砖,瓷砖的面积是多少平方米?
(10×2+6×2)×2+10×6
=32×2+60
=124(平方米)
五、生活中的数学问题
1.这个长方体的鱼池,长10米,宽6米,深是2米。
③在离池面的0.5米处有一道红色的水位线,水位线有多长?
(10+6)×2=32(米)
五、生活中的数学问题
1.这个长方体的鱼池,长10米,宽6米,深是2米。
④鱼池内放满水后能盛放多少立方米的水?
10×6×2=120(立方米)
想一想,议一议,做一做:
你能用一张长方形的纸做一个通风管,你能做出什么形状?配什么形状的底面?(不浪费纸张的情况下,接头处忽略不计)
根据所填数据,你发现了什么?
通风管形状 侧面积/cm2 底面积/cm2 高/cm 表面积/cm2 体积/cm3
动手做一做,将计算结果记录下来。(得数保留两位小数)
填写下表
20.7厘米
10厘米
你能把这张纸做一个的圆柱,体积是多少?
20.7厘米
10厘米
--2r---
---------------2∏r-----------
a3
abh
兀r2h
sh
圆柱和圆锥有什么特点?
底面
侧面
底面
底面
侧面
3个面,2个大小相等的圆(底面)和1个曲面(侧面)。
2个面,1个圆(底面)和1个曲面(侧面)。
底面
侧面
底面
3.一种笔记本的包装箱,标明的尺寸(单位:mm)是350×260×40。它的体积是多少立方分米?
二、试一试
立体图形的复习
这是我们学过的立体图形,
如果把它们分为两类,可以怎么样分呢?
名称 顶点 棱 面 体
长方体
8个
12条
(分为4组,以相交于同一顶点的三条棱为一组)
(分为3组,有4长、4宽、4高)
L=4a+4b+4h
L=4(a+b+h)
L=12a
6个
(相对的面完全相同)
(有两个相对的面是正方形,其余四个都是完全相同的长方形)
S表=(ab+ah+bh) ×2
(六个面完全相同)
S表=2a +4ab
S表=6a
V=S底h
=abh
V=S底h
=a
(a,a,a)
正方体
(a,b,h)
(a,a,h)
名称 高 底面 侧面 表面积 体积
圆柱
圆锥
(上下一样粗细)
无数条
(上底和下底的距离)
(有一个顶点)
2个
1个
1条
(顶点到圆心的距离)
曲面
S底=πr
S底=πr
曲面
V锥=
S底h÷3=πr h÷3
S侧=ch=πdh
=2πrh
S表=
2S底+S侧
沿高展开是个长方形
沿母线展开后是扇形
V柱=S底h=πr h
V=
V=
V=
V=
abh
a
3
πr h
1
3
πr h
V = sh
正方体、长方体和圆柱有什么相似的地方呢?
h
a
b
a
a
a
s
h
s
h
16平方米
8
米
9
米
15平方米
你会计算它们的体积吗?
立体图形
生活中变式题型
生活中基本题型
基本概念
体积
面积
棱
25cm
20cm
30cm
20cm
20cm
20cm
20cm
20cm
20cm
20cm
立体图形
生活中变式题型
生活中基本题型
基本概念
体积
面积
棱
体积变化
表面变化
棱
综合运用
1.将一个棱长25cm的正方体框架改成长方体,已知长方体长25cm,宽20cm,求高是多少厘米?
25×12 ÷ 4-25-20=30(cm)
答:长方体高是30cm。
2.用十字捆扎法将下面蛋糕进行捆扎,接头
处25cm,求绳子的长度。
25cm
20cm
30cm
d=25cm
30cm
25 ×2 +20 ×2 +30 ×4
+ 25=235(cm)
答:绳长235cm。
25 ×4 +30 ×4 + 25=245(cm)
答:绳长245cm。
3.(1)把长方体的高减少2cm,就变成了一个正方体,
已知表面积减少56cm ,求原来长方体的体积。
2cm
28cm
56 ÷2 =28(cm)
7 +2 =9(cm)
7 × 7 × 9=441(cm )
答:原来长方体体积441cm 。
(2)把圆柱的高减少2cm,表面积就减少25.12cm ,已知原来圆柱的高为9cm,求原来长方体的体积。
2cm
12.56cm
7cm
25.12 ÷2 =12.56(cm)
12.56 ÷ 3.14 ÷ 2 =2(cm)
2 π ×9 =36π(cm )
答:原来圆柱的体积是36πcm 。
28÷4 =7(cm)
4.(1)已知长方体的横截面为12cm ,沿横截面将其
分成若干个小长方体(如图),表面积增加多少平方厘米?
12 ×2 =24(cm )
3 - 1 = 2(次)
2 ×2 =4(个)
12 ×2 =24(cm )
(n - 1) × 2×12
n个
一刀两断
4.(2)已知圆柱的横截面为12cm ,沿横截面将其分成
若干个小圆柱(如图),表面积增加多少平方厘米?
n个
一刀两断
12 ×2 =24(cm )
3 - 1 = 2(次)
2 ×2 =4(个)
12 ×2 =24(cm )
(n - 1) × 2×12
4.(3)已知圆柱的底面直径是6cm,高是8cm,沿轴线将
其分成两个相等的半圆柱,表面积增加多少平方厘米?
6cm
8cm
6 ×8 × 2=96(cm )
答:表面积增加了96cm 。
5.把一个圆柱切成若干等分,拼成一个近似的长方体,已知圆柱的半径和高均为10cm。那么长方体的表面积比圆柱增加了多少平方厘米
10 × 10 ×2 =200cm
10
厘
米
6.长方体的长15cm,宽10cm,高8cm,将两个这样的长方体
叠放在一起,组成的新长方体的表面积可能是多少平方厘米?
(30,10,8)
(30 × 10 +30 ×8 + 10×8) × 2=1240(cm )
(15,20,8)
(15 × 20 +15×8 + 20×8) × 2=1160(cm )
(15,10,16)
(15 × 10 +15×16 + 10×16) × 2=1100(cm )
7.将8个正方体熔铸成和它等底等高的圆柱,可以熔铸
几个?如果熔铸成圆锥呢?
正方体
圆柱
8个
8个
1 :1
圆锥
24个
1 :3
8.一个圆锥形状的沙堆,底面周长是31.4米,高1.5米。将这堆沙铺成宽2m、高0.1m的长方体,可以铺多长?
3.14×52×1.5×
=3.14×12.5
=39.25(立方米)
314÷3.14÷2=5(米)
39.25÷2÷0.1=196.25(米)
答:可以铺196.25米。
9.测量不规则的物体可以采用转化的策略。圆柱的半径是5cm,高是10cm,将其盛满水,放入一块石子,然后将石子取出,水面下降了4cm,求石子的体积。
5 π×4=100π(cm )
答:石子的体积是100πcm 。
10.圆柱里有一半水,将其倒入与它等底等高的圆锥中,还剩10L水,那么,你知道圆柱的容积吗?
1
10 ÷( - )=60(L)
1
3
1
2
答:圆柱的容积是60L。
11.把一个圆柱切成若干等分,拼成一个近似的长方体。圆柱的侧面积是72平方米,底面半径是3米。求圆柱的体积是多少?
72÷2×3
圆柱的体积=侧面积÷2×半径
底面积
× 高
12.一个用塑料薄膜覆盖的草莓大棚,长15米,横截面是一个半径2米的半圆。
①大棚内的空间有多少大?
22×π×15÷2
=3.14×4×15÷2
=3.14×30
=94.2(立方米)
12.一个用塑料薄膜覆盖的蔬菜大棚,长15米,横截面是一个半径2米的半圆。
②覆盖在这个大棚上的塑料薄膜约有多少平方米?
3.14×22+3.14×22×15÷2
=3.14×(4+30)
=3.14×34
=106.76(平方米)
谢 谢 指 导 !
底面
侧面
底面
高
底面
侧面
高
立体图形
生活中变式题型
生活中基本题型
基本概念
说说下列各图是由哪些基本图形组成的。
长方体的表面积= (上 面 + 前 面 + 侧 面 )×2
=(长×宽+长×高+宽×高)×2
S=(ab+ah+bh)×2
下面
前面
后面
左面
右面
上面
棱长1厘米的正方体,体积是1立方厘米
长5厘米
宽4厘米
高3厘米
长方体的体积正好等于它的长、宽、高的乘积。
长方体的体积=长×宽×高
V=abh
正方体的表面积=一个面的面积×6
S=a2 × 6
棱长4厘米
棱长4厘米
棱长4厘米
因为正方体是长、宽、高都相等的长方体,所以
正方体的体积=棱长×棱长×棱长
V=
·
a
a
a
·
V=
3
a
或
底面周长
高
底面
底面
侧面
S侧=ch=πdh=2πrh
底面积
高
怎样求圆柱的体积呢?
圆柱体积的大小与哪些条件有关?
因为长方体的体积=底面积×高
所以圆柱的体积=底面积×高
V = S h
底面
h
h
r
r
πr
V= πr × h
2
V长方体 = V圆柱
= πr × h
2
V=abh
V=Sh
= πr ×r × h
圆柱体积=底面积 高
1
3
圆锥体积=
底面积 高
底面
侧面
底面
曲面
扇形
名称 高 底面 侧面 表面积 体积
圆柱
(上下一样粗细) 无数条
(上底和下底的距离) 2个
S底=πr 曲面
沿高展开是个长方形
S侧=ch=πdh
=2πrh
S表=
2S底+S侧 V柱=S底h=πr h
圆锥
(有一个顶点) 1条
(顶点到圆心) 1个
S底=πr 曲面
沿母线展开后是扇形 V锥=
S底h=πr h
三、 判断(对的打“√ ”,错的打“× ”。)
3.下图中的正方体、圆柱和圆锥底
面积相等,高也相等。圆锥的体积是
正方体的 。 ( )
√
3
1
三、 判断(对的打“√ ”,错的打“× ”。)
1.一个圆柱形的水桶能装水15升,我们就说水桶的体积是15立方分米。
………………( )
×
三、判断(对的打“√ ”,错的打“× ”。)
2.一个长方体的长、宽、高分别是a米、b米、h米。如果高增加2米,体积比原来增加2ab立方米
……………… ( )
√
四、选择正确答案的序号填入括号里
1. 把一个圆柱的底面平均分成若干个扇形,然后切开拼成一个近似的长方体。下面哪句话是正确的?( )
A、表面积和体积都没变
B、表面积和体积都发生了变化
C、表面积变了,体积没变
D、表面积没变,体积变了
C
四、选择正确答案的序号填入括号里
A、 54 B、 18
C 、 0.6 D、 6
2. 等底等体积的圆柱和圆锥,圆锥的高是18厘米,那么圆柱的高是( )厘米。
D
四、选择正确答案的序号填入括号里
3. 等高等体积的圆柱和圆锥,圆柱的底面积是6平方厘米,那么圆锥的底面积是( )平方厘米。
A、6 B、18
C、2 D、36
B
四、选择正确答案的序号填入括号里
4.把一个底面半径是2分米、高是3分米的圆柱形容器中注满水,现垂直轻轻插入一根底面积是5平方分米,高是4分米的方钢,溢出水的体积是( )毫升。
A、20 B、15
C、20000 D、15000
D
五、生活中的数学问题
1.这个长方体的鱼池,长10米,宽6米,深是2米。
①这个这个鱼池的占地面积是多少平方米?
10×6=60(平方米)
五、生活中的数学问题
1.这个长方体的鱼池,长10米,宽6米,深是2米。
②在池内的侧面和池底铺上瓷砖,瓷砖的面积是多少平方米?
(10×2+6×2)×2+10×6
=32×2+60
=124(平方米)
五、生活中的数学问题
1.这个长方体的鱼池,长10米,宽6米,深是2米。
③在离池面的0.5米处有一道红色的水位线,水位线有多长?
(10+6)×2=32(米)
五、生活中的数学问题
1.这个长方体的鱼池,长10米,宽6米,深是2米。
④鱼池内放满水后能盛放多少立方米的水?
10×6×2=120(立方米)
想一想,议一议,做一做:
你能用一张长方形的纸做一个通风管,你能做出什么形状?配什么形状的底面?(不浪费纸张的情况下,接头处忽略不计)
根据所填数据,你发现了什么?
通风管形状 侧面积/cm2 底面积/cm2 高/cm 表面积/cm2 体积/cm3
动手做一做,将计算结果记录下来。(得数保留两位小数)
填写下表
20.7厘米
10厘米
你能把这张纸做一个的圆柱,体积是多少?
20.7厘米
10厘米
--2r---
---------------2∏r-----------
a3
abh
兀r2h
sh
圆柱和圆锥有什么特点?
底面
侧面
底面
底面
侧面
3个面,2个大小相等的圆(底面)和1个曲面(侧面)。
2个面,1个圆(底面)和1个曲面(侧面)。
底面
侧面
底面
3.一种笔记本的包装箱,标明的尺寸(单位:mm)是350×260×40。它的体积是多少立方分米?
二、试一试
