六年级数学下册课件-7.2.7立体图形的表面积和体积苏教版(共15张ppt)
文档属性
| 名称 | 六年级数学下册课件-7.2.7立体图形的表面积和体积苏教版(共15张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 305.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 11:55:25 | ||
图片预览




文档简介
(共15张PPT)
学习目标:
1、理解并掌握立体图形的表面积和体积、容积的含义,计算方法,并形成知识体系。
2、正确、灵活应用公式进行计算。
3、能应用所学知识解决实际问题。
小组合作交流:
1、什么是长方体、正方体和圆柱的表面积?各怎样计算?
2、什么是物体的体积?什么是容器的容积?常用的体积单位有哪些?相邻单位间的进率各是多少?
3、回忆各立体图形体积公式的推导过程,想想它们之间的联系,用你喜欢的方法整理归纳。
前
一个长方体的纸盒,将它展开后,得到什么样的图形?
上
下
左
右
后
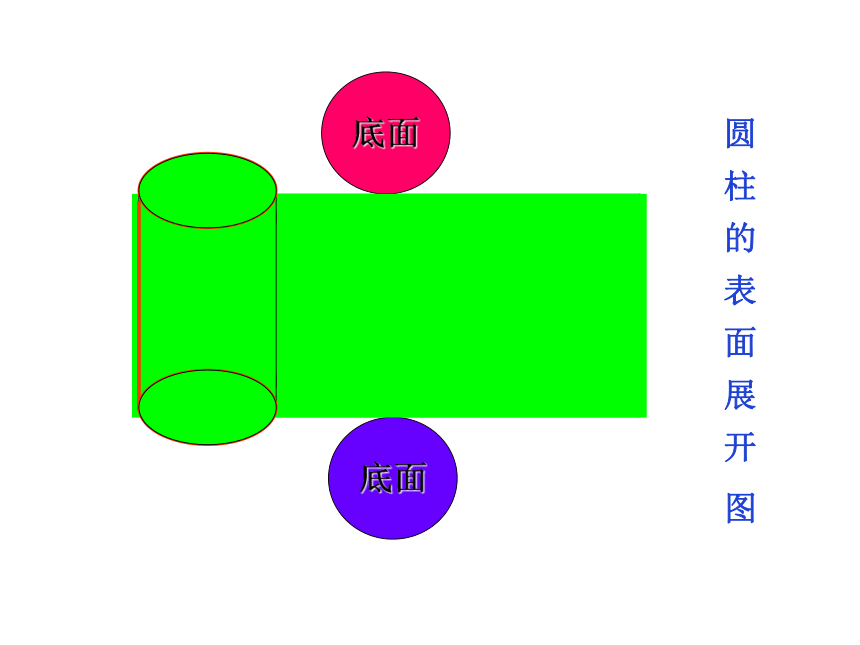
底面
底面
底面
底面
底面周长
高
圆 柱 的 表 面 展 开 图
填表
图形 已知条件 表面积 体积
长方体 长4m 宽3m 高2m ( ) ( )
正方体 棱长3dm ( ) ( )
圆柱 底面半径2cm 高5cm ( ) ( )
圆锥 底面半径10cm 高6cm ( )
挑战第一关
制作一个圆柱形的油桶,至少需要多少铁皮,是求圆柱形油桶的( )。
挑战第二关
棱长是6厘米的正方体,表面积和体积相等。( )
挑战第三关
一个圆柱和一个圆锥等底等高,它们的体积相差12立方分米,这个圆柱的体积是( )立方分米,圆锥的体积是( )立方分米。
课堂检测
1、单选题(20分)
选择我最棒。(把正确答案的序号填在括号里)
把一根圆柱形木料削成一个最大的圆锥,削去部分的体积是圆锥体积的( )。
A.2倍 B. 3倍 C. 12 D.13
2、单选题(20分)
如果把圆柱的底面积扩大到原来的5倍,高不变,它的体积扩大到原来的( )倍。
A. 25 B. 5 C.10
3、填空(30分)
在括号里填合适的单位。
(1)一间卧室地面的面积是15( )。
(2)一瓶牛奶大约有250( )。
(3)一间教室的空间大约是144( )。
(4)一台微波炉的体积是92( ),容积是25( )。
4、一个长方体金鱼缸,长40厘米,宽40厘米,高35厘米。它左侧面的玻璃打碎了,要重新配一块。重新配上的玻璃是多少平方厘米?是多少平方分米?(30分)
一个圆柱形玻璃容器的底面直径是20厘米。把一块铁块从这个容器的水中取出后,水面下降2厘米。这块铁块的体积是多少?
学习目标:
1、理解并掌握立体图形的表面积和体积、容积的含义,计算方法,并形成知识体系。
2、正确、灵活应用公式进行计算。
3、能应用所学知识解决实际问题。
小组合作交流:
1、什么是长方体、正方体和圆柱的表面积?各怎样计算?
2、什么是物体的体积?什么是容器的容积?常用的体积单位有哪些?相邻单位间的进率各是多少?
3、回忆各立体图形体积公式的推导过程,想想它们之间的联系,用你喜欢的方法整理归纳。
前
一个长方体的纸盒,将它展开后,得到什么样的图形?
上
下
左
右
后
底面
底面
底面
底面
底面周长
高
圆 柱 的 表 面 展 开 图
填表
图形 已知条件 表面积 体积
长方体 长4m 宽3m 高2m ( ) ( )
正方体 棱长3dm ( ) ( )
圆柱 底面半径2cm 高5cm ( ) ( )
圆锥 底面半径10cm 高6cm ( )
挑战第一关
制作一个圆柱形的油桶,至少需要多少铁皮,是求圆柱形油桶的( )。
挑战第二关
棱长是6厘米的正方体,表面积和体积相等。( )
挑战第三关
一个圆柱和一个圆锥等底等高,它们的体积相差12立方分米,这个圆柱的体积是( )立方分米,圆锥的体积是( )立方分米。
课堂检测
1、单选题(20分)
选择我最棒。(把正确答案的序号填在括号里)
把一根圆柱形木料削成一个最大的圆锥,削去部分的体积是圆锥体积的( )。
A.2倍 B. 3倍 C. 12 D.13
2、单选题(20分)
如果把圆柱的底面积扩大到原来的5倍,高不变,它的体积扩大到原来的( )倍。
A. 25 B. 5 C.10
3、填空(30分)
在括号里填合适的单位。
(1)一间卧室地面的面积是15( )。
(2)一瓶牛奶大约有250( )。
(3)一间教室的空间大约是144( )。
(4)一台微波炉的体积是92( ),容积是25( )。
4、一个长方体金鱼缸,长40厘米,宽40厘米,高35厘米。它左侧面的玻璃打碎了,要重新配一块。重新配上的玻璃是多少平方厘米?是多少平方分米?(30分)
一个圆柱形玻璃容器的底面直径是20厘米。把一块铁块从这个容器的水中取出后,水面下降2厘米。这块铁块的体积是多少?
