人教版数学八年级下册 18.2.1 第1课时 矩形的性质 课件 (共19张PPT)
文档属性
| 名称 | 人教版数学八年级下册 18.2.1 第1课时 矩形的性质 课件 (共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 714.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 07:18:37 | ||
图片预览




文档简介
(共19张PPT)
第十八章 平行四边形
18.2.1 矩 形
第1课时 矩形的性质
1.理解矩形的概念,知道矩形与平行四边形的区别与联系.
2.会证明矩形的性质,会用矩形的性质解决简单的问题.
3.掌握直角三角形斜边中线的性质,并会简单的运用.
重点难点:
1.理解矩形的概念,掌握直角三角形斜边中线的性质,并会简单的运用.
2.会证明矩形的性质,会用矩形的性质解决简单的问题.
学习目标:
情景导入
观察下面图形,长方形在生活中无处不在.
思考 长方形跟我们前面学行四边形有什么关系?
知识精讲
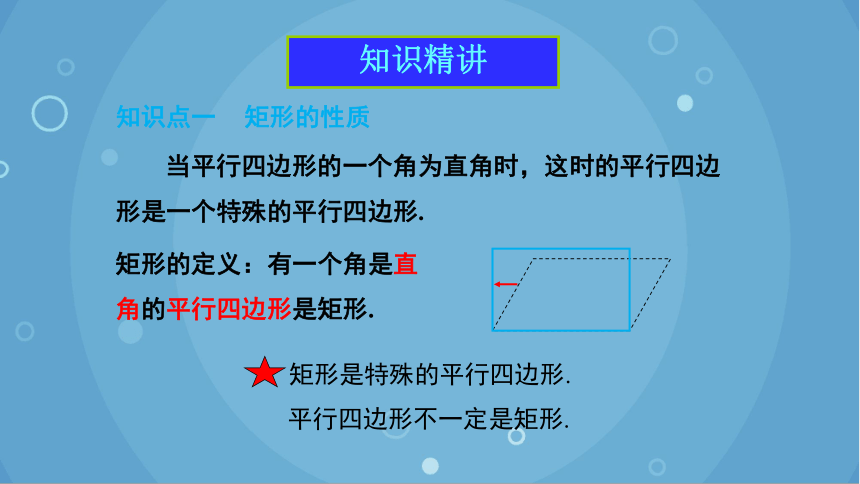
知识点一 矩形的性质
当平行四边形的一个角为直角时,这时的平行四边形是一个特殊的平行四边形.
矩形的定义:有一个角是直角的平行四边形是矩形.
矩形是特殊的平行四边形.
平行四边形不一定是矩形.
命题1:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°.
A
B
C
D
证明: ∵四边形ABCD是矩形,
∴ ∠A=90°.
又∵矩形ABCD是平行四边形,
∴ ∠A=∠C , ∠B = ∠D,∠A +∠B = 180°.
∴ ∠A=∠B=∠C=∠D=90°.即矩形的四个角都是直角.
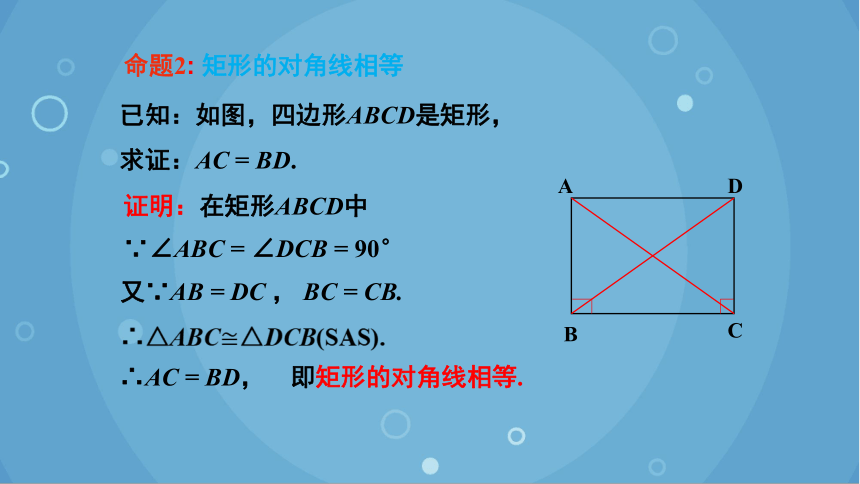
已知:如图,四边形ABCD是矩形,
求证:AC = BD.
A
B
C
D
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB.
∴AC = BD, 即矩形的对角线相等.
命题2: 矩形的对角线相等
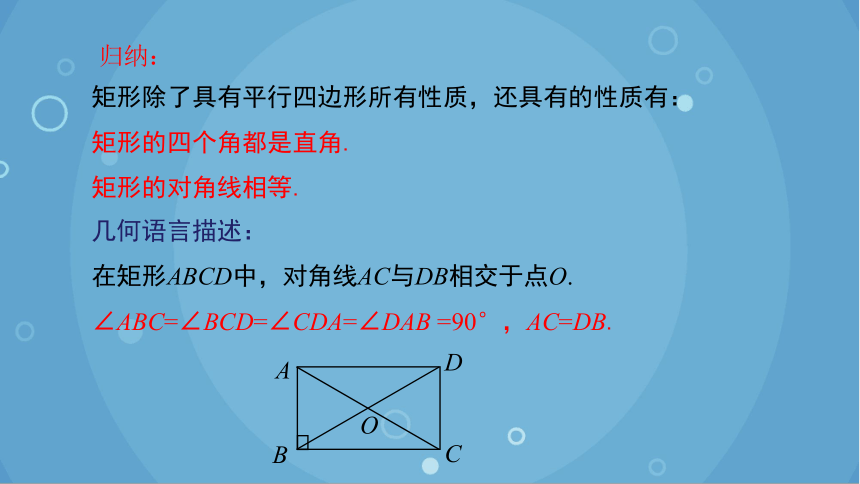
矩形除了具有平行四边形所有性质,还具有的性质有:
矩形的四个角都是直角.
矩形的对角线相等.
几何语言描述:
在矩形ABCD中,对角线AC与DB相交于点O.
∠ABC=∠BCD=∠CDA=∠DAB =90°,AC=DB.
A
B
C
D
O
归纳:
例1 如图,在矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE ,垂足为F.求证:DF=DC.
A
B
C
D
E
F
证明:连接DE.
∵AD =AE,∴∠AED =∠ADE.
∵四边形ABCD是矩形,
∴AD∥BC,∠C=90°.
∴∠ADE=∠DEC,∴∠DEC=∠AED.
又∵DF⊥AE, ∴DF=DC.
针对练习
1.如图,在矩形ABCD中,对角线AC,BD交于点O,
下列说法错误的是 ( )
A.AB∥DC B.AC=BD
C.AC⊥BD D.OA=OB
A
B
C
D
O
C
2.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD面积的_________.
知识点二 直角三角形斜边上的中线的性质
命题3:直角三角形斜边上的中线等于斜边的一半.
O
C
B
A
D
证明: 延长BO至D, 使OD=BO,连接AD、DC.∵AO=OC, BO=OD,
∴四边形ABCD是平行四边形.
∵∠ABC=90°,
∴平行四边形ABCD是矩形,
∴AC=BD,
如图,在Rt△ABC中,∠ABC=90°,BO是AC上的中线.求证: BO = AC
∴BO= BD= AC.
例2 如图,已知BD,CE是△ABC不同边上的高,点G,F分别是BC,DE的中点,试说明GF⊥DE.
解:连接EG,DG.∵BD,CE是△ABC的高,
∴∠BDC=∠BEC=90°.
∵点G是BC的中点,∴EG= BC,
DG= BC.∴EG=DG.
又∵点F是DE的中点,∴GF⊥DE.
归纳:在直角三角形中,遇到斜边中点常作斜边中线,进而可将问题转化为等腰三角形的问题,然后利用等腰三角形“三线合一”的性质解题.
针对练习
1.如图,在△ABC中,∠ABC = 90°,BD是斜边AC上的中线.
(1)若BD=3cm,则AC =_____cm;
(2)若∠C = 30° ,AB = 5cm,则AC =_____cm, BD = _____cm.
A
B
C
D
6
10
5
当堂检测
1.矩形具有而一般平行四边形不具有的性质是 ( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分
2.若直角三角形的两条直角边分别5和12,则斜边上的中线长为 ( )
A.13 B.6 C.6.5 D.不能确定
A
C
3.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则EF=______cm.
2.5
4.如图,△ABC中,E在AC上,且BE⊥AC.D为AB中点,若DE=5,AE=8,则BE的长为______.
6
第4题图
第5题图
5.如图,四边形ABCD是矩形,对角线AC,BD相交于点O,BE∥AC交DC的延长线于点E.
(1)求证:BD=BE,
(2)若∠DBC=30° , BO=4 ,求四边形ABED的面积.
A
B
C
D
O
E
(1)证明:∵四边形ABCD是矩形,
∴AC= BD,AB∥CD.
又∵BE∥AC,
∴四边形ABEC是平行四边形,
∴AC=BE,
∴BD=BE.
(2)解:∵在矩形ABCD中,BO=4,
∴BD = 2BO =2×4=8.
∵∠DBC=30°,
∴CD= BD= ×8=4,
∴AB=CD=4,DE=CD+CE=CD+AB=8.
在Rt△BCD中,
BC=
∴四边形ABED的面积= ×(4+8)× = .
A
B
C
D
O
E
6.如图,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,PE⊥AC,PF⊥BD于F,求PE+PF的值.
解:连接OP.
∵四边形ABCD是矩形,
∴∠DAB=90°,OA=OD=OC=OB,
∴S△AOD=S△DOC=S△AOB=S△BOC
= S矩形ABCD= ×6×8=12.
在Rt△BAD中,由勾股定理得BD=10,
∴AO=OD=5,
∵S△APO+S△DPO=S△AOD,
∴ AO·PE+ DO·PF=12,即5PE+5PF=24,
∴PE+PF= .
矩形的相关概念及性质
具有平行四边形的一切性质
四个内角都是直角,
两条对角线互相平分且相等
轴对称图形
有两条对称轴
直角三角形斜边上的中线等于斜边的一半
有一个角是直角的平行四边形叫做矩形
课堂小结
第十八章 平行四边形
18.2.1 矩 形
第1课时 矩形的性质
1.理解矩形的概念,知道矩形与平行四边形的区别与联系.
2.会证明矩形的性质,会用矩形的性质解决简单的问题.
3.掌握直角三角形斜边中线的性质,并会简单的运用.
重点难点:
1.理解矩形的概念,掌握直角三角形斜边中线的性质,并会简单的运用.
2.会证明矩形的性质,会用矩形的性质解决简单的问题.
学习目标:
情景导入
观察下面图形,长方形在生活中无处不在.
思考 长方形跟我们前面学行四边形有什么关系?
知识精讲
知识点一 矩形的性质
当平行四边形的一个角为直角时,这时的平行四边形是一个特殊的平行四边形.
矩形的定义:有一个角是直角的平行四边形是矩形.
矩形是特殊的平行四边形.
平行四边形不一定是矩形.
命题1:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°.
A
B
C
D
证明: ∵四边形ABCD是矩形,
∴ ∠A=90°.
又∵矩形ABCD是平行四边形,
∴ ∠A=∠C , ∠B = ∠D,∠A +∠B = 180°.
∴ ∠A=∠B=∠C=∠D=90°.即矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形,
求证:AC = BD.
A
B
C
D
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB.
∴AC = BD, 即矩形的对角线相等.
命题2: 矩形的对角线相等
矩形除了具有平行四边形所有性质,还具有的性质有:
矩形的四个角都是直角.
矩形的对角线相等.
几何语言描述:
在矩形ABCD中,对角线AC与DB相交于点O.
∠ABC=∠BCD=∠CDA=∠DAB =90°,AC=DB.
A
B
C
D
O
归纳:
例1 如图,在矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE ,垂足为F.求证:DF=DC.
A
B
C
D
E
F
证明:连接DE.
∵AD =AE,∴∠AED =∠ADE.
∵四边形ABCD是矩形,
∴AD∥BC,∠C=90°.
∴∠ADE=∠DEC,∴∠DEC=∠AED.
又∵DF⊥AE, ∴DF=DC.
针对练习
1.如图,在矩形ABCD中,对角线AC,BD交于点O,
下列说法错误的是 ( )
A.AB∥DC B.AC=BD
C.AC⊥BD D.OA=OB
A
B
C
D
O
C
2.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD面积的_________.
知识点二 直角三角形斜边上的中线的性质
命题3:直角三角形斜边上的中线等于斜边的一半.
O
C
B
A
D
证明: 延长BO至D, 使OD=BO,连接AD、DC.∵AO=OC, BO=OD,
∴四边形ABCD是平行四边形.
∵∠ABC=90°,
∴平行四边形ABCD是矩形,
∴AC=BD,
如图,在Rt△ABC中,∠ABC=90°,BO是AC上的中线.求证: BO = AC
∴BO= BD= AC.
例2 如图,已知BD,CE是△ABC不同边上的高,点G,F分别是BC,DE的中点,试说明GF⊥DE.
解:连接EG,DG.∵BD,CE是△ABC的高,
∴∠BDC=∠BEC=90°.
∵点G是BC的中点,∴EG= BC,
DG= BC.∴EG=DG.
又∵点F是DE的中点,∴GF⊥DE.
归纳:在直角三角形中,遇到斜边中点常作斜边中线,进而可将问题转化为等腰三角形的问题,然后利用等腰三角形“三线合一”的性质解题.
针对练习
1.如图,在△ABC中,∠ABC = 90°,BD是斜边AC上的中线.
(1)若BD=3cm,则AC =_____cm;
(2)若∠C = 30° ,AB = 5cm,则AC =_____cm, BD = _____cm.
A
B
C
D
6
10
5
当堂检测
1.矩形具有而一般平行四边形不具有的性质是 ( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分
2.若直角三角形的两条直角边分别5和12,则斜边上的中线长为 ( )
A.13 B.6 C.6.5 D.不能确定
A
C
3.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则EF=______cm.
2.5
4.如图,△ABC中,E在AC上,且BE⊥AC.D为AB中点,若DE=5,AE=8,则BE的长为______.
6
第4题图
第5题图
5.如图,四边形ABCD是矩形,对角线AC,BD相交于点O,BE∥AC交DC的延长线于点E.
(1)求证:BD=BE,
(2)若∠DBC=30° , BO=4 ,求四边形ABED的面积.
A
B
C
D
O
E
(1)证明:∵四边形ABCD是矩形,
∴AC= BD,AB∥CD.
又∵BE∥AC,
∴四边形ABEC是平行四边形,
∴AC=BE,
∴BD=BE.
(2)解:∵在矩形ABCD中,BO=4,
∴BD = 2BO =2×4=8.
∵∠DBC=30°,
∴CD= BD= ×8=4,
∴AB=CD=4,DE=CD+CE=CD+AB=8.
在Rt△BCD中,
BC=
∴四边形ABED的面积= ×(4+8)× = .
A
B
C
D
O
E
6.如图,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,PE⊥AC,PF⊥BD于F,求PE+PF的值.
解:连接OP.
∵四边形ABCD是矩形,
∴∠DAB=90°,OA=OD=OC=OB,
∴S△AOD=S△DOC=S△AOB=S△BOC
= S矩形ABCD= ×6×8=12.
在Rt△BAD中,由勾股定理得BD=10,
∴AO=OD=5,
∵S△APO+S△DPO=S△AOD,
∴ AO·PE+ DO·PF=12,即5PE+5PF=24,
∴PE+PF= .
矩形的相关概念及性质
具有平行四边形的一切性质
四个内角都是直角,
两条对角线互相平分且相等
轴对称图形
有两条对称轴
直角三角形斜边上的中线等于斜边的一半
有一个角是直角的平行四边形叫做矩形
课堂小结
