华东师大版数学七年级下册 9.1.1 第1课时 三角形的有关概念 课件 (共20张PPT)
文档属性
| 名称 | 华东师大版数学七年级下册 9.1.1 第1课时 三角形的有关概念 课件 (共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 08:41:37 | ||
图片预览







文档简介
(共20张PPT)
9.1 三角形
9.1.1 认识三角形
第1课时 三角形的有关概念
情境引入
学习目标
1.认识三角形并会用几何语言表示三角形,了解三角形分类。
2.掌握三角形的三边关系。(难点)
导入新课
问题引入
埃及金字塔
水分子结构示意图
飞机机翼
问题:
(1)从古埃及的金字塔到现代的飞机,从宏伟的建筑物到微小的分子结构,都有什么样的形象?
(2)在我们的生活中有没有这样的形象呢?试举例。
讲授新课
三角形的概念
一
问题1:观察下面三角形的形成过程,说一说什么叫三角形
定义:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
问题2:三角形中有几条线段 有几个角
A
B
C
有三条线段,三个角
边:线段AB,BC,CA是三角形的边.
顶点:点A,B,C是三角形的顶点,
角:∠A,∠B,∠C叫做三角形的内角,简称三角形的角.
记法:三角形ABC用符号表示________.
边的表示:三角形ABC的边AB、AC和BC可用小写字母分别表
示为________.
△ABC
c,a,b
边c
边b
边a
顶点C
角
角
角
顶点A
顶点B
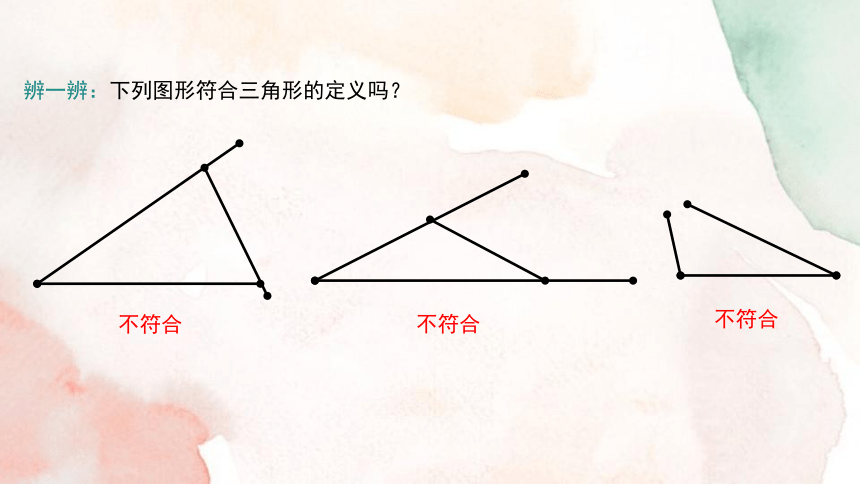
辨一辨:下列图形符合三角形的定义吗?
不符合
不符合
不符合
①位置关系:不在同一直线上;②联接方式:首尾顺次.
三角形应满足以下两个条件:
要点提醒
表示方法:
三角形用符号“△”表示;记作“△ABC”,读作“三角形ABC”,除此△ABC还可记作△BCA, △ CAB, △ ACB等.
基本要素:
三角形的边:边AB、BC、CA;
三角形的顶点:顶点A、B、C;
三角形的内角(简称为三角形的角):∠ A、 ∠ B、 ∠ C.
特别规定:
三角形ABC的三边,一般的顶点A所对的边记作a,顶点B所对的边记作b,顶点C所对的边记作c.
找一找:(1)图中有几个三角形?用符号表示出这些三角形?
A
B
C
D
E
5个,它们分别是△ABE,△ABC, △BEC,△BCD,△ECD.
(2)以AB为边的三角形有哪些?
△ABC、△ABE.
(3)以E为顶点的三角形有哪些?
△ ABE 、△BCE、 △CDE.
(4)以∠D为角的三角形有哪些?
△ BCD、 △DEC.
(5)说出△BCD的三个角和三个顶点所对的边.
△BCD的三个角是∠BCD、∠BDC、∠CBD.顶点B所对应的边为DC,顶点C所对应的边为BD,顶点D所对应的边为BC.
问题3: 如图,把△ABC的一边BC延长,得到∠ACD.它与 △ABC有和联系呢?
像这样,三角形的一边与另一边的延长线所组成的角,叫作三角形的外角.
对外角∠ACD来说,∠ACB是与它相邻的内角,∠A,∠B是与它不相邻的内角.
D
三角形的分类
二
问题1:按照三角形内角的大小,三角形可以分为哪几类?
由图可发现,在三角形中, 三个角都是锐角的三角形叫锐角三角形, 有一个角是直角的三角形叫直角三角形, 有一个角是钝角的三角形叫钝角三角形.
锐角三角形
直角三角形
钝角三角形
(1)等腰三角形和等边三角形的区别是什么
(2)从边上来说,除了等腰三角形和等边三角形还有什么样
的三角形
(3)根据上面的内容思考:怎样对三角形进行分类?
等腰三角形两边相等,等边三角形三边相等.
三边都不相等的三角形.
问题2:如果以三角形边的元素的不同,三角形该如何分类呢?
等边三角形
等腰三角形
不等边三角形
(
顶角
(
底角
(
底角
按是否有边相等分
三角形
不等边三角形
等腰
三角形
底和腰不相等的等腰三角形
等边三角形
按内角大小分
三角形
锐角三角形
直角三角形
钝角三角形
腰
底边
当堂练习
1.三角形是指( )
A.由三条线段所组成的封闭图形
B.由不在同一直线上的三条直线首尾顺次相接组成
的图形
C.由不在同一直线上的三条线段首尾顺次相接组成
的图形
D.由三条线段首尾顺次相接组成的图形
C
2.判断:
(2)等边三角形是特殊的等腰三角形.( )
(1)一个钝角三角形一定不是等腰三角形.( )
√
×
(3)等腰三角形的腰和底一定不相等.( )
×
(4)等边三角形是锐角三角形.( )
(5)直角三角形一定不是等腰三角形.( )
×
√
3.如图,在△ACE中,∠CEA的对边是 .
A
B
F
E
D
C
AC
课堂小结
三角形
定义及其基本要素
顶点、角、边
分类
按角分类
按边分类分类
不重不漏
9.1 三角形
9.1.1 认识三角形
第1课时 三角形的有关概念
情境引入
学习目标
1.认识三角形并会用几何语言表示三角形,了解三角形分类。
2.掌握三角形的三边关系。(难点)
导入新课
问题引入
埃及金字塔
水分子结构示意图
飞机机翼
问题:
(1)从古埃及的金字塔到现代的飞机,从宏伟的建筑物到微小的分子结构,都有什么样的形象?
(2)在我们的生活中有没有这样的形象呢?试举例。
讲授新课
三角形的概念
一
问题1:观察下面三角形的形成过程,说一说什么叫三角形
定义:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
问题2:三角形中有几条线段 有几个角
A
B
C
有三条线段,三个角
边:线段AB,BC,CA是三角形的边.
顶点:点A,B,C是三角形的顶点,
角:∠A,∠B,∠C叫做三角形的内角,简称三角形的角.
记法:三角形ABC用符号表示________.
边的表示:三角形ABC的边AB、AC和BC可用小写字母分别表
示为________.
△ABC
c,a,b
边c
边b
边a
顶点C
角
角
角
顶点A
顶点B
辨一辨:下列图形符合三角形的定义吗?
不符合
不符合
不符合
①位置关系:不在同一直线上;②联接方式:首尾顺次.
三角形应满足以下两个条件:
要点提醒
表示方法:
三角形用符号“△”表示;记作“△ABC”,读作“三角形ABC”,除此△ABC还可记作△BCA, △ CAB, △ ACB等.
基本要素:
三角形的边:边AB、BC、CA;
三角形的顶点:顶点A、B、C;
三角形的内角(简称为三角形的角):∠ A、 ∠ B、 ∠ C.
特别规定:
三角形ABC的三边,一般的顶点A所对的边记作a,顶点B所对的边记作b,顶点C所对的边记作c.
找一找:(1)图中有几个三角形?用符号表示出这些三角形?
A
B
C
D
E
5个,它们分别是△ABE,△ABC, △BEC,△BCD,△ECD.
(2)以AB为边的三角形有哪些?
△ABC、△ABE.
(3)以E为顶点的三角形有哪些?
△ ABE 、△BCE、 △CDE.
(4)以∠D为角的三角形有哪些?
△ BCD、 △DEC.
(5)说出△BCD的三个角和三个顶点所对的边.
△BCD的三个角是∠BCD、∠BDC、∠CBD.顶点B所对应的边为DC,顶点C所对应的边为BD,顶点D所对应的边为BC.
问题3: 如图,把△ABC的一边BC延长,得到∠ACD.它与 △ABC有和联系呢?
像这样,三角形的一边与另一边的延长线所组成的角,叫作三角形的外角.
对外角∠ACD来说,∠ACB是与它相邻的内角,∠A,∠B是与它不相邻的内角.
D
三角形的分类
二
问题1:按照三角形内角的大小,三角形可以分为哪几类?
由图可发现,在三角形中, 三个角都是锐角的三角形叫锐角三角形, 有一个角是直角的三角形叫直角三角形, 有一个角是钝角的三角形叫钝角三角形.
锐角三角形
直角三角形
钝角三角形
(1)等腰三角形和等边三角形的区别是什么
(2)从边上来说,除了等腰三角形和等边三角形还有什么样
的三角形
(3)根据上面的内容思考:怎样对三角形进行分类?
等腰三角形两边相等,等边三角形三边相等.
三边都不相等的三角形.
问题2:如果以三角形边的元素的不同,三角形该如何分类呢?
等边三角形
等腰三角形
不等边三角形
(
顶角
(
底角
(
底角
按是否有边相等分
三角形
不等边三角形
等腰
三角形
底和腰不相等的等腰三角形
等边三角形
按内角大小分
三角形
锐角三角形
直角三角形
钝角三角形
腰
底边
当堂练习
1.三角形是指( )
A.由三条线段所组成的封闭图形
B.由不在同一直线上的三条直线首尾顺次相接组成
的图形
C.由不在同一直线上的三条线段首尾顺次相接组成
的图形
D.由三条线段首尾顺次相接组成的图形
C
2.判断:
(2)等边三角形是特殊的等腰三角形.( )
(1)一个钝角三角形一定不是等腰三角形.( )
√
×
(3)等腰三角形的腰和底一定不相等.( )
×
(4)等边三角形是锐角三角形.( )
(5)直角三角形一定不是等腰三角形.( )
×
√
3.如图,在△ACE中,∠CEA的对边是 .
A
B
F
E
D
C
AC
课堂小结
三角形
定义及其基本要素
顶点、角、边
分类
按角分类
按边分类分类
不重不漏
