华东师大版数学七年级下册10.3.2旋转的特征 课件 (共20张PPT)
文档属性
| 名称 | 华东师大版数学七年级下册10.3.2旋转的特征 课件 (共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 346.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 08:45:30 | ||
图片预览



文档简介
(共20张PPT)
数学 七年级下册 华师版
10.3 旋转
10.3.2 旋转的特征
第10章 轴对称、平移与旋转
知识点 旋转的特征
1.下列关于图形旋转的特征说法错误的是( )
A.图形的形状与大小不变
B.对应线段相等,对应角相等
C.图形上每一个点到旋转中心的距离相等
D.图形上每一个点旋转的角度相同
C
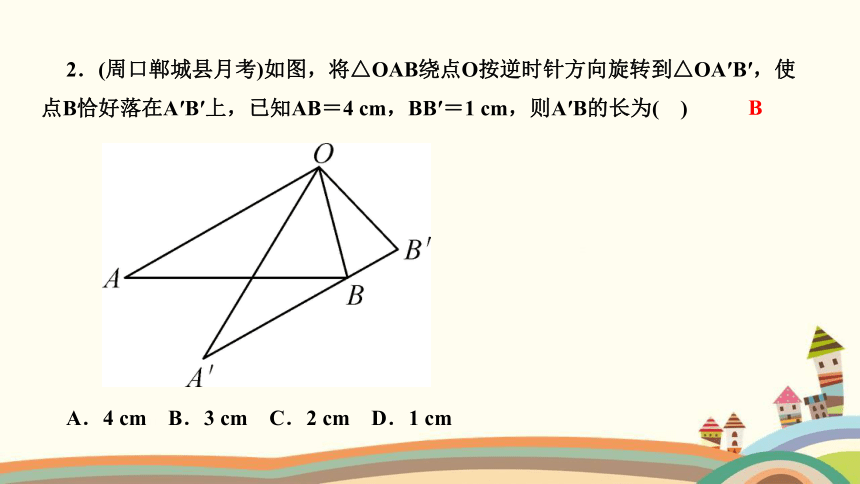
2.(周口郸城县月考)如图,将△OAB绕点O按逆时针方向旋转到△OA′B′,使点B恰好落在A′B′上,已知AB=4 cm,BB′=1 cm,则A′B的长为( )
A.4 cm B.3 cm C.2 cm D.1 cm
B
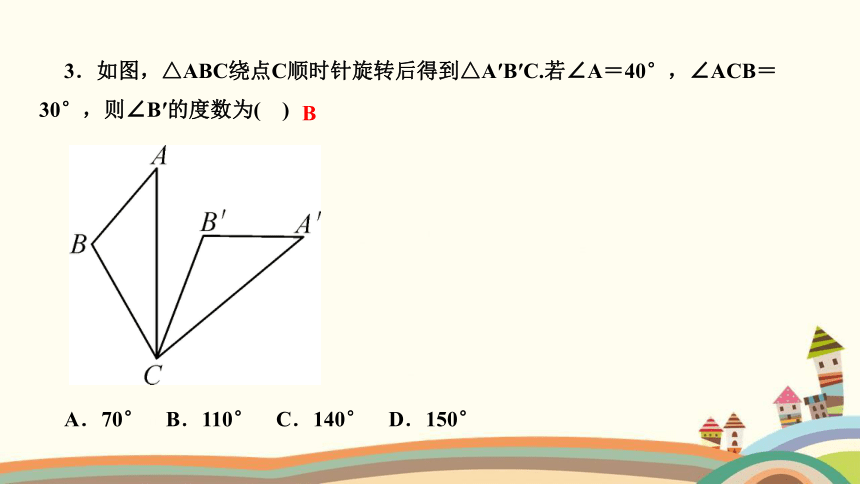
3.如图,△ABC绕点C顺时针旋转后得到△A′B′C.若∠A=40°,∠ACB=30°,则∠B′的度数为( )
A.70° B.110° C.140° D.150°
B
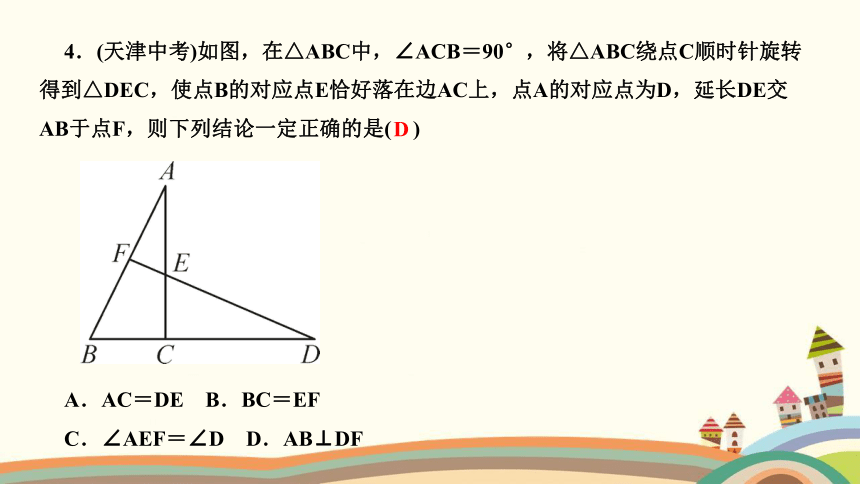
4.(天津中考)如图,在△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,使点B的对应点E恰好落在边AC上,点A的对应点为D,延长DE交AB于点F,则下列结论一定正确的是( )
A.AC=DE B.BC=EF
C.∠AEF=∠D D.AB⊥DF
D
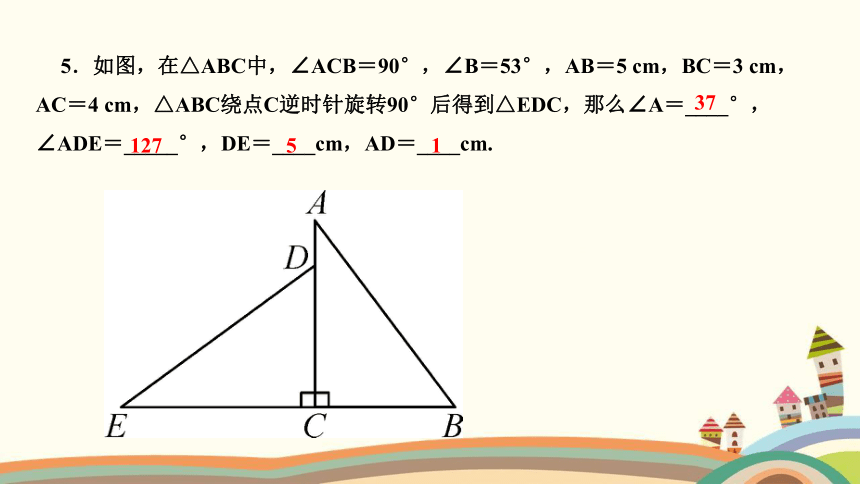
5.如图,在△ABC中,∠ACB=90°,∠B=53°,AB=5 cm,BC=3 cm,AC=4 cm,△ABC绕点C逆时针旋转90°后得到△EDC,那么∠A=____°,∠ADE=_____°,DE=____cm,AD=____cm.
37
127
5
1
6.如图,在等边△ABC中,AB=6,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为____.
2
7.如图,将△ABC绕点C按顺时针方向旋转至△A′B′C,使点A′落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB′=____度.
46
知识点 旋转作图
8.(教材P122练习T3变式)如图,在正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1.在正方形网格中,作出△AB1C1.
解:画图略
9.(2021·大连)如图,在△ABC中,∠ACB=90°,∠BAC=α,将△ABC绕点C顺时针旋转90°得到△A′B′C,点B的对应点B′在边AC上(不与点A,C重合),则∠AA′B′的度数为( )
A.α B.α-45°
C.45°-α D.90°-α
C
10.(贺州中考)如图,将Rt △ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连结BB′,若∠A′B′B=20°,则∠A的度数是____.
65°
11.以图1(以点O为圆心,半径为1 的半圆)作为“基本图形”,分别经历如下变换能得到图2的序号是_______.
①只要向右平移1个单位;②先以直线AB为对称轴进行对称变换,再向右平移1个单位;③先绕点O旋转180°,再向右平移1个单位;④只要绕着某点旋转180°.
②③④
12.(教材P122练习T1变式)如图所示的图形可以看作正三角形OAB绕某一点旋转而生成的,那么旋转中心是哪一个点?旋转了多少次?每一次旋转了多少度?
解:旋转中心是点O,一共旋转了5次,每次旋转了60°
13.(淮安中考)如图,方格纸上每个小正方形的边长均为1个单位长度,点A,B都在格点上(两条网格线的交点叫格点).
(1)将线段AB向上平移两个单位长度,点A的对应点为点A1,点B的对应点为点B1,请画出平移后的线段A1B1;
(2)将线段A1B1绕点A1按逆时针方向旋转90°,点B1的对应点为点B2,请画出旋转后的线段A1B2;
(3)连接AB2,BB2,求△ABB2的面积.
14.(教材P125习题T2变式)如图,正方形ABCD的边长为5,点F为正方形ABCD内的点,△BFC经逆时针旋转后能与△BEA重合.
(1)旋转中心是哪一点?旋转了多少度?
(2)判断△BEF是怎样的三角形,并说明理由;
(3)若∠BFC=90°,试说明AE∥BF.
解:(1)旋转中心是点B,旋转了90°
(2)△BEF是等腰直角三角形,理由如下:因为由旋转的特征可知BE=BF,∠EBF=∠ABC,又因为四边形ABCD为正方形,所以∠ABC=90°,所以∠EBF=90°,所以△BEF是等腰直角三角形
(3)由旋转的特征可知,∠EBF=∠ABC,∠BEA=∠BFC.因为∠ABC=90°,所以∠EBF=∠ABC=90°.又因为∠BFC=90°,所以∠BEA=∠BFC=90°.所以∠EBF+∠BEA=180°,所以AE∥BF
15.如图,在直角△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE,FG相交于点H.判断线段DE,FG有怎样的大小关系和位置关系?并说明理由.
解:DE=FG,DE⊥FG.理由如下:因为由旋转的特征可知AC=DE,∠ACB=∠DEB,又因为由平移的特征可知AC=FG,∠ACB=∠FGE,∠ABC=∠FEG=90°,所以DE=FG,∠DEB=∠FGE.因为∠FEG=90°,所以∠DEB+∠DEG=90°,所以∠FGE+∠DEG=90°.又因为∠FGE+∠DEG+∠EHG=180°,所以90°+∠EHG=180°,即∠EHG=90°,所以DE⊥FG
数学 七年级下册 华师版
10.3 旋转
10.3.2 旋转的特征
第10章 轴对称、平移与旋转
知识点 旋转的特征
1.下列关于图形旋转的特征说法错误的是( )
A.图形的形状与大小不变
B.对应线段相等,对应角相等
C.图形上每一个点到旋转中心的距离相等
D.图形上每一个点旋转的角度相同
C
2.(周口郸城县月考)如图,将△OAB绕点O按逆时针方向旋转到△OA′B′,使点B恰好落在A′B′上,已知AB=4 cm,BB′=1 cm,则A′B的长为( )
A.4 cm B.3 cm C.2 cm D.1 cm
B
3.如图,△ABC绕点C顺时针旋转后得到△A′B′C.若∠A=40°,∠ACB=30°,则∠B′的度数为( )
A.70° B.110° C.140° D.150°
B
4.(天津中考)如图,在△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,使点B的对应点E恰好落在边AC上,点A的对应点为D,延长DE交AB于点F,则下列结论一定正确的是( )
A.AC=DE B.BC=EF
C.∠AEF=∠D D.AB⊥DF
D
5.如图,在△ABC中,∠ACB=90°,∠B=53°,AB=5 cm,BC=3 cm,AC=4 cm,△ABC绕点C逆时针旋转90°后得到△EDC,那么∠A=____°,∠ADE=_____°,DE=____cm,AD=____cm.
37
127
5
1
6.如图,在等边△ABC中,AB=6,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为____.
2
7.如图,将△ABC绕点C按顺时针方向旋转至△A′B′C,使点A′落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB′=____度.
46
知识点 旋转作图
8.(教材P122练习T3变式)如图,在正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1.在正方形网格中,作出△AB1C1.
解:画图略
9.(2021·大连)如图,在△ABC中,∠ACB=90°,∠BAC=α,将△ABC绕点C顺时针旋转90°得到△A′B′C,点B的对应点B′在边AC上(不与点A,C重合),则∠AA′B′的度数为( )
A.α B.α-45°
C.45°-α D.90°-α
C
10.(贺州中考)如图,将Rt △ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连结BB′,若∠A′B′B=20°,则∠A的度数是____.
65°
11.以图1(以点O为圆心,半径为1 的半圆)作为“基本图形”,分别经历如下变换能得到图2的序号是_______.
①只要向右平移1个单位;②先以直线AB为对称轴进行对称变换,再向右平移1个单位;③先绕点O旋转180°,再向右平移1个单位;④只要绕着某点旋转180°.
②③④
12.(教材P122练习T1变式)如图所示的图形可以看作正三角形OAB绕某一点旋转而生成的,那么旋转中心是哪一个点?旋转了多少次?每一次旋转了多少度?
解:旋转中心是点O,一共旋转了5次,每次旋转了60°
13.(淮安中考)如图,方格纸上每个小正方形的边长均为1个单位长度,点A,B都在格点上(两条网格线的交点叫格点).
(1)将线段AB向上平移两个单位长度,点A的对应点为点A1,点B的对应点为点B1,请画出平移后的线段A1B1;
(2)将线段A1B1绕点A1按逆时针方向旋转90°,点B1的对应点为点B2,请画出旋转后的线段A1B2;
(3)连接AB2,BB2,求△ABB2的面积.
14.(教材P125习题T2变式)如图,正方形ABCD的边长为5,点F为正方形ABCD内的点,△BFC经逆时针旋转后能与△BEA重合.
(1)旋转中心是哪一点?旋转了多少度?
(2)判断△BEF是怎样的三角形,并说明理由;
(3)若∠BFC=90°,试说明AE∥BF.
解:(1)旋转中心是点B,旋转了90°
(2)△BEF是等腰直角三角形,理由如下:因为由旋转的特征可知BE=BF,∠EBF=∠ABC,又因为四边形ABCD为正方形,所以∠ABC=90°,所以∠EBF=90°,所以△BEF是等腰直角三角形
(3)由旋转的特征可知,∠EBF=∠ABC,∠BEA=∠BFC.因为∠ABC=90°,所以∠EBF=∠ABC=90°.又因为∠BFC=90°,所以∠BEA=∠BFC=90°.所以∠EBF+∠BEA=180°,所以AE∥BF
15.如图,在直角△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE,FG相交于点H.判断线段DE,FG有怎样的大小关系和位置关系?并说明理由.
解:DE=FG,DE⊥FG.理由如下:因为由旋转的特征可知AC=DE,∠ACB=∠DEB,又因为由平移的特征可知AC=FG,∠ACB=∠FGE,∠ABC=∠FEG=90°,所以DE=FG,∠DEB=∠FGE.因为∠FEG=90°,所以∠DEB+∠DEG=90°,所以∠FGE+∠DEG=90°.又因为∠FGE+∠DEG+∠EHG=180°,所以90°+∠EHG=180°,即∠EHG=90°,所以DE⊥FG
