北师大版七年级数学下册 4.1 认识三角形 课件(共29张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 4.1 认识三角形 课件(共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 920.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 09:01:17 | ||
图片预览






文档简介
(共34张PPT)
第四章 三角形
4.1.1 认识三角形
学习目标
掌握三角形的概念,能指出三角形的顶点、边、角等基
本元素,能用适当的符号表示三角形以及这些基本元素。
经历探索、验证“三角形内角和等于180°”的活动过程
获得一定的推理活动经验 。
会按角的大小关系对三角形分类,能判断出给定三角形
的形状.
由不在同一直线的
三条线段
首尾顺次连接所组成的图形叫三角形。
C
B
A
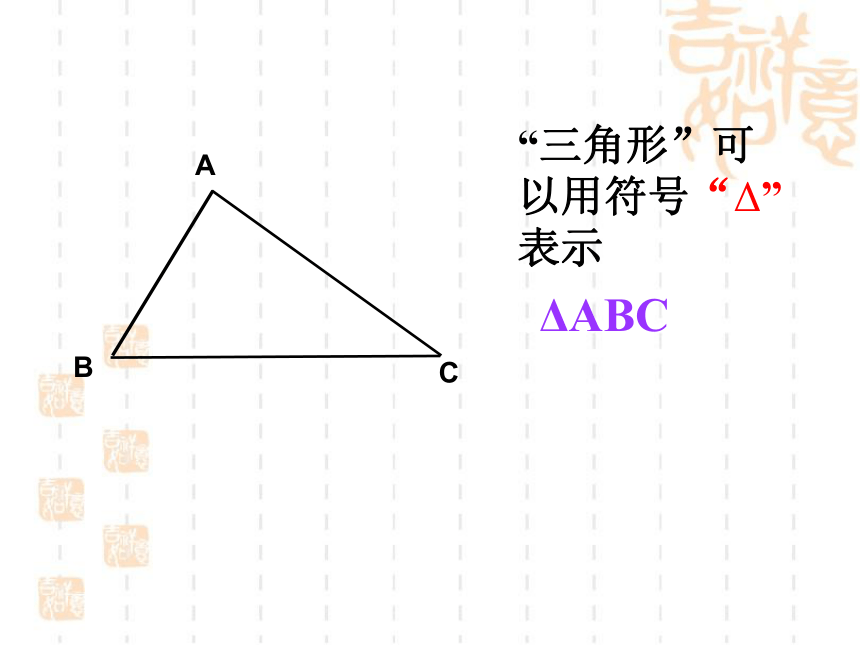
“三角形”可以用符号“Δ”表示
ΔABC
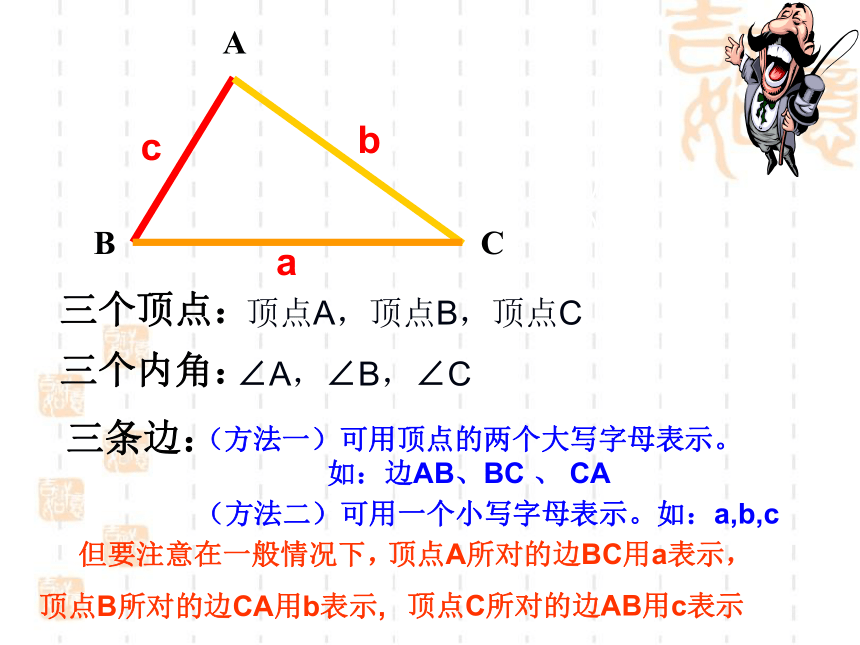
三个顶点:
三个内角:
三条边:
A
B
C
顶点A,顶点B,顶点C
∠A,∠B,∠C
(方法一)可用顶点的两个大写字母表示。 如:边AB、BC 、 CA
a
b
c
(方法二)可用一个小写字母表示。如:a,b,c
但要注意在一般情况下,
顶点A所对的边BC用a表示,
顶点B所对的边CA用b表示,
顶点C所对的边AB用c表示。
ΔBFD, ΔAFD, ΔADE, ΔAGE, ΔEGC
ΔABD, ΔAEC
ΔABE, ΔADC
你会吗
?
请你找出下图中的三角形,并用符号表示出来。
它们分别是:
A
B
C
D
E
F
G
ΔABC
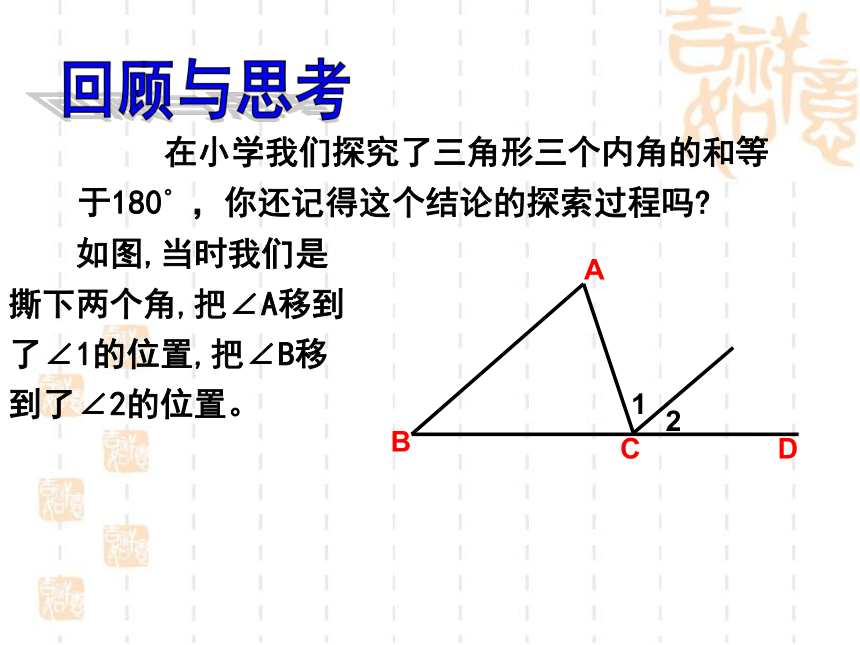
在小学我们探究了三角形三个内角的和等于180 ,你还记得这个结论的探索过程吗
1
A
B
D
2
C
如图,当时我们是撕下两个角,把∠A移到了∠1的位置,把∠B移到了∠2的位置。
拼一拼,说一说
如果只撕下一个角,你能用学过的知识拼凑并解释“三角形的三个内角和是180 ”吗?
1
2
3
1
2
3
(1)将∠1撕下,并按下图进行摆放,其中∠1的顶点与∠2的顶点重合,它的一条边与∠2的一条边重合.此时∠1的另一条边b与∠3的一条边a 平行吗 为什么
1
a
b
1
2
3
1
a
b
(2)将∠2与∠3的公共边延长,它与b所夹的角为∠4. ∠3与∠4的大小有什么关系?为什么?
4
C
A
B
E
F
证法3:
过A作EF∥BC
C
A
B
E
证法4:
过A作AE∥BC
由此你能得到什么结论?
三角形的三个内角和等于180度.
下面的图⑴、图⑵、图⑶中的三角形被遮住的两个内角是什么角?试着说明理由。
三角形的分类
锐角三角形
三个内角都是锐角
钝角三角形
有一个内角是钝角
直角三角形
有一个内角是直角
直角边
直角边
斜边
1.常用符号“Rt ABC”来表示
直角三角形ABC.
2.直角三角形的两个锐角之间
有什么关系?
直角三角形的两个锐角互余
A
C
B
一个三角形中可能有两个直角吗?可能有两个钝角或锐角吗?
1.观察下面的三角形,并把它们的标号填入相应图内:
锐角三角形 直角三角形 钝角三角形
③⑤
①④⑥
②⑦
2.一个三角形两个内角的度数分别如下,这个三角形是什么三角形
(1)30度和60度
(2)40度和70度
(3)50度和20度
直角三角形
锐角三角形
钝角三角形
3.在下面的空白处,分别填入“锐角”,“钝角”
或“直角”:
(1)如果三角形的三个内角都相等,那么这个三角形是 三角形;
(2)如果三角形的一个内角等于另外两个 内角之和,那么这个三角形是 三角形;
锐角
直角
4. 已知∠A,∠B,∠C是△ABC的三个内角,∠A=70°,∠C=30 °, ∠B=( ).
5.直角三角形一个锐角为70°,另一个锐角等于( ).
80 °
20 °
1. △ABC中, ∠A:∠B:∠C=2:3:4,则
∠A= , ∠B= , ∠C= .
2.在△ABC中,∠A=80°,∠B=∠C,则∠C=( ).
40°
80°
60°
50°
1.三角形定义:由不在同一直线的三条线段
首尾顺次连接所组成的图形叫三角形。
2.三角形三个内角的和等于180 。
3.三角形按角的大小分类:
⑴锐角三角形 :三个内角都是锐角;
⑵直角三角形 :有一个内角为直角;
⑶钝角三角形 :有一个内角为钝角 。
4.直角三角形的两个锐角互余。
以三角形为主设计一幅美丽图案并说说你的设计意图,作品我们将公开展览。
2、请你做个“小小设计师”
1 、知识技能第1题
3.已知∠ACB=90°,CD⊥AB,垂足为D.
⑴ 图中有几个直角三角形?是哪几个?分别说出它们的直角边和斜边。
⑵ ∠ACD和∠A有什么关系?
C
B
A
D
Rt BDC 直角边是BD 、CD,斜边BC
Rt ADC 直角边是AD、CD, 斜边AC
解:(1) Rt ACB 直角边是AC、BC, 斜边AB
(2)∠ACD和∠A互余
在Rt ADC中,∵ CD⊥AB , ∴∠ADC =90°
又∵ ∠ACD+∠A + ∠ADC =180°
∴ ∠ACD+∠A =90°
30 °
70 °
B
C
A
E
解:(1)∵∠ABC+∠CBE= 180°
∴ ∠ABC= 180°-∠CBE
= 180°- 70°= 110°
∴在 ABC中, ∠ACB = 180°- ∠ABC - ∠A
= 180°- 110° - 30°
= 40°
如图,一艘轮船按箭头所示方向行驶,C处有一灯塔,请你根据图中所标数据求∠ACB的大小,当轮船距离灯塔C最近时,∠ACB是多少度?
B
30 °
90 °
C
A
解:当轮船距离灯塔C最近时,则有CB⊥AB,
即∠ACB = 90°
∴在 ABC中, ∠ACB= 180°- ∠ABC - ∠A
= 180°- 90° - 30°
= 60°
如图,一艘轮船按箭头所示方向行驶,C处有一灯塔,请你根据图中所标数据求∠ACB的大小,当轮船距离灯塔C最近时,∠ACB是多少度?
直线外一点与直线上各点连接的所有线段中( )最短
垂线段
第四章 三角形
4.1.1 认识三角形
学习目标
掌握三角形的概念,能指出三角形的顶点、边、角等基
本元素,能用适当的符号表示三角形以及这些基本元素。
经历探索、验证“三角形内角和等于180°”的活动过程
获得一定的推理活动经验 。
会按角的大小关系对三角形分类,能判断出给定三角形
的形状.
由不在同一直线的
三条线段
首尾顺次连接所组成的图形叫三角形。
C
B
A
“三角形”可以用符号“Δ”表示
ΔABC
三个顶点:
三个内角:
三条边:
A
B
C
顶点A,顶点B,顶点C
∠A,∠B,∠C
(方法一)可用顶点的两个大写字母表示。 如:边AB、BC 、 CA
a
b
c
(方法二)可用一个小写字母表示。如:a,b,c
但要注意在一般情况下,
顶点A所对的边BC用a表示,
顶点B所对的边CA用b表示,
顶点C所对的边AB用c表示。
ΔBFD, ΔAFD, ΔADE, ΔAGE, ΔEGC
ΔABD, ΔAEC
ΔABE, ΔADC
你会吗
?
请你找出下图中的三角形,并用符号表示出来。
它们分别是:
A
B
C
D
E
F
G
ΔABC
在小学我们探究了三角形三个内角的和等于180 ,你还记得这个结论的探索过程吗
1
A
B
D
2
C
如图,当时我们是撕下两个角,把∠A移到了∠1的位置,把∠B移到了∠2的位置。
拼一拼,说一说
如果只撕下一个角,你能用学过的知识拼凑并解释“三角形的三个内角和是180 ”吗?
1
2
3
1
2
3
(1)将∠1撕下,并按下图进行摆放,其中∠1的顶点与∠2的顶点重合,它的一条边与∠2的一条边重合.此时∠1的另一条边b与∠3的一条边a 平行吗 为什么
1
a
b
1
2
3
1
a
b
(2)将∠2与∠3的公共边延长,它与b所夹的角为∠4. ∠3与∠4的大小有什么关系?为什么?
4
C
A
B
E
F
证法3:
过A作EF∥BC
C
A
B
E
证法4:
过A作AE∥BC
由此你能得到什么结论?
三角形的三个内角和等于180度.
下面的图⑴、图⑵、图⑶中的三角形被遮住的两个内角是什么角?试着说明理由。
三角形的分类
锐角三角形
三个内角都是锐角
钝角三角形
有一个内角是钝角
直角三角形
有一个内角是直角
直角边
直角边
斜边
1.常用符号“Rt ABC”来表示
直角三角形ABC.
2.直角三角形的两个锐角之间
有什么关系?
直角三角形的两个锐角互余
A
C
B
一个三角形中可能有两个直角吗?可能有两个钝角或锐角吗?
1.观察下面的三角形,并把它们的标号填入相应图内:
锐角三角形 直角三角形 钝角三角形
③⑤
①④⑥
②⑦
2.一个三角形两个内角的度数分别如下,这个三角形是什么三角形
(1)30度和60度
(2)40度和70度
(3)50度和20度
直角三角形
锐角三角形
钝角三角形
3.在下面的空白处,分别填入“锐角”,“钝角”
或“直角”:
(1)如果三角形的三个内角都相等,那么这个三角形是 三角形;
(2)如果三角形的一个内角等于另外两个 内角之和,那么这个三角形是 三角形;
锐角
直角
4. 已知∠A,∠B,∠C是△ABC的三个内角,∠A=70°,∠C=30 °, ∠B=( ).
5.直角三角形一个锐角为70°,另一个锐角等于( ).
80 °
20 °
1. △ABC中, ∠A:∠B:∠C=2:3:4,则
∠A= , ∠B= , ∠C= .
2.在△ABC中,∠A=80°,∠B=∠C,则∠C=( ).
40°
80°
60°
50°
1.三角形定义:由不在同一直线的三条线段
首尾顺次连接所组成的图形叫三角形。
2.三角形三个内角的和等于180 。
3.三角形按角的大小分类:
⑴锐角三角形 :三个内角都是锐角;
⑵直角三角形 :有一个内角为直角;
⑶钝角三角形 :有一个内角为钝角 。
4.直角三角形的两个锐角互余。
以三角形为主设计一幅美丽图案并说说你的设计意图,作品我们将公开展览。
2、请你做个“小小设计师”
1 、知识技能第1题
3.已知∠ACB=90°,CD⊥AB,垂足为D.
⑴ 图中有几个直角三角形?是哪几个?分别说出它们的直角边和斜边。
⑵ ∠ACD和∠A有什么关系?
C
B
A
D
Rt BDC 直角边是BD 、CD,斜边BC
Rt ADC 直角边是AD、CD, 斜边AC
解:(1) Rt ACB 直角边是AC、BC, 斜边AB
(2)∠ACD和∠A互余
在Rt ADC中,∵ CD⊥AB , ∴∠ADC =90°
又∵ ∠ACD+∠A + ∠ADC =180°
∴ ∠ACD+∠A =90°
30 °
70 °
B
C
A
E
解:(1)∵∠ABC+∠CBE= 180°
∴ ∠ABC= 180°-∠CBE
= 180°- 70°= 110°
∴在 ABC中, ∠ACB = 180°- ∠ABC - ∠A
= 180°- 110° - 30°
= 40°
如图,一艘轮船按箭头所示方向行驶,C处有一灯塔,请你根据图中所标数据求∠ACB的大小,当轮船距离灯塔C最近时,∠ACB是多少度?
B
30 °
90 °
C
A
解:当轮船距离灯塔C最近时,则有CB⊥AB,
即∠ACB = 90°
∴在 ABC中, ∠ACB= 180°- ∠ABC - ∠A
= 180°- 90° - 30°
= 60°
如图,一艘轮船按箭头所示方向行驶,C处有一灯塔,请你根据图中所标数据求∠ACB的大小,当轮船距离灯塔C最近时,∠ACB是多少度?
直线外一点与直线上各点连接的所有线段中( )最短
垂线段
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
