北师大版数学八年级下册 3.2 第1课时 旋转的性质 课件 (共14张PPT)
文档属性
| 名称 | 北师大版数学八年级下册 3.2 第1课时 旋转的性质 课件 (共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 391.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 09:09:08 | ||
图片预览


文档简介
(共14张PPT)
第三章 图形的平移与旋转
3.2 图形的旋转
第1课时 旋转的性质
1.下列运动属于旋转的是( )
A.滚动过程中的篮球的滚动
B.钟表的钟摆的摆动
C.气球升空的运动
D.一个图形沿某直线对折的过程
2.(枣庄中考)将数字“6”旋转180°,得到数字“9”;将数字“9”旋转180°,得到数字“6”.现将数字“69”旋转180°,得到的数字是( )
A.96 B.69 C.66 D.99
B
B
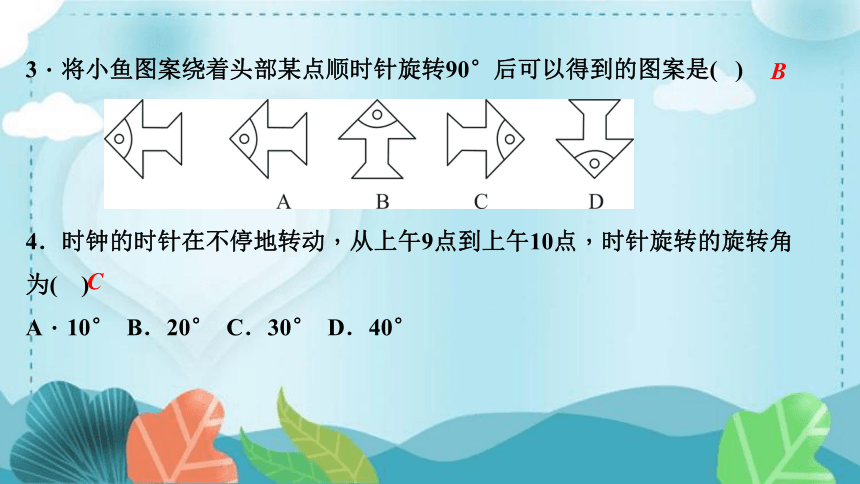
3.将小鱼图案绕着头部某点顺时针旋转90°后可以得到的图案是( )
4.时钟的时针在不停地转动,从上午9点到上午10点,时针旋转的旋转角为( )
A.10° B.20° C.30° D.40°
B
C
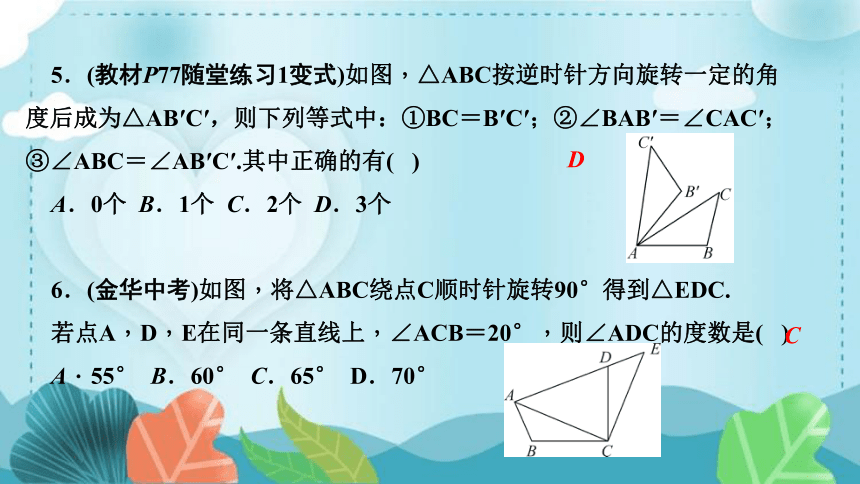
5.(教材P77随堂练习1变式)如图,△ABC按逆时针方向旋转一定的角度后成为△AB′C′,则下列等式中:①BC=B′C′;②∠BAB′=∠CAC′;③∠ABC=∠AB′C′.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
6.(金华中考)如图,将△ABC绕点C顺时针旋转90°得到△EDC.
若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
A.55° B.60° C.65° D.70°
D
C
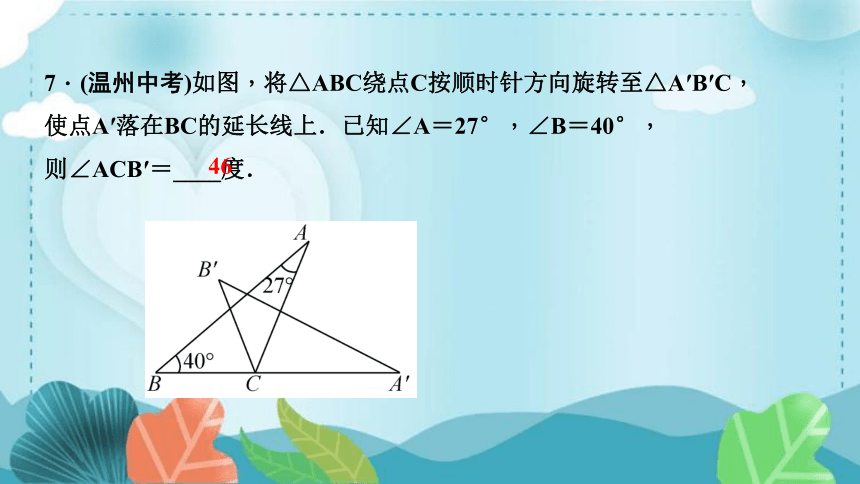
7.(温州中考)如图,将△ABC绕点C按顺时针方向旋转至△A′B′C,
使点A′落在BC的延长线上.已知∠A=27°,∠B=40°,
则∠ACB′=____度.
46
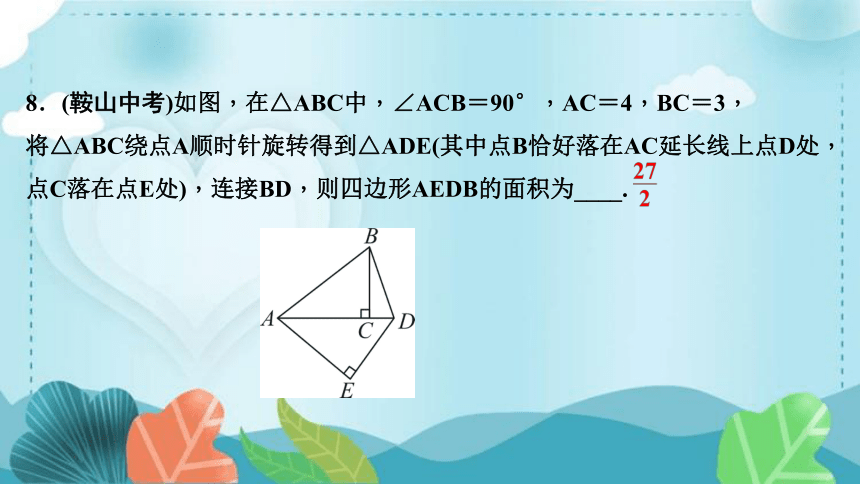
8.(鞍山中考)如图,在△ABC中,∠ACB=90°,AC=4,BC=3,
将△ABC绕点A顺时针旋转得到△ADE(其中点B恰好落在AC延长线上点D处,点C落在点E处),连接BD,则四边形AEDB的面积为____.
9.(大连中考)如图,将△ABC绕点B逆时针旋转α,得到△EBD,
若点A恰好在ED的延长线上,则∠CAD的度数为( )
A.90°-α B.α
C.180°-α D.2α
C
D
C
12.如图,△ABC是等边三角形,点D是BC上的一点,
△ABD按逆时针方向旋转后到达△ACP的位置.
(1)旋转中心是点A;
(2)旋转角的度数为60°;
(3)求证:△ADP是等边三角形.
证明:∵由旋转的性质知PA=DA,
且旋转角∠DAP=∠BAC=60°,∴△ADP是等边三角形
13.如图,已知正方形ABCD中的△DCF可以经过旋转得到△BCE.
(1)图中哪一个点是旋转中心?△DCF按什么方向旋转了多少度?
(2)如果CF=3 cm,连接EF,求EF的长.
14.如图,在△ABC中,∠ACB=90°,∠B=30°,
以点C为旋转中心,将△ABC旋转到△A′B′C的位置,
使A′B′经过点A.
(1)求∠ACA′的度数;
(2)求线段AC与线段A′B′的数量关系.
解:(1)∵∠ACB=90°,∠B=30°,∴∠BAC=60°,
由旋转的性质可知,CA=CA′,∠A′=∠BAC=60°,
∴△ACA′为等边三角形,∴∠ACA′=60°
15.(达州期末)△ABC和△EFG是两块完全重合的等边三角形纸片(如图①所示),O是AC(或EF)的中点,△ABC不动,将△EFG绕O点顺时针转α(0°<α°<120°).
(1)试分别说明α是多少度时,点F在△ABC外部、BC上、内部(不证明)
(2)当点F不在BC上时,在图②,图③两种情况下(设EF或延长线与BC交于P,EG与CA或延长线交于Q),分别写出OP与OQ的数量关系,并从图②,③中选一种情况给予证明.
第三章 图形的平移与旋转
3.2 图形的旋转
第1课时 旋转的性质
1.下列运动属于旋转的是( )
A.滚动过程中的篮球的滚动
B.钟表的钟摆的摆动
C.气球升空的运动
D.一个图形沿某直线对折的过程
2.(枣庄中考)将数字“6”旋转180°,得到数字“9”;将数字“9”旋转180°,得到数字“6”.现将数字“69”旋转180°,得到的数字是( )
A.96 B.69 C.66 D.99
B
B
3.将小鱼图案绕着头部某点顺时针旋转90°后可以得到的图案是( )
4.时钟的时针在不停地转动,从上午9点到上午10点,时针旋转的旋转角为( )
A.10° B.20° C.30° D.40°
B
C
5.(教材P77随堂练习1变式)如图,△ABC按逆时针方向旋转一定的角度后成为△AB′C′,则下列等式中:①BC=B′C′;②∠BAB′=∠CAC′;③∠ABC=∠AB′C′.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
6.(金华中考)如图,将△ABC绕点C顺时针旋转90°得到△EDC.
若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
A.55° B.60° C.65° D.70°
D
C
7.(温州中考)如图,将△ABC绕点C按顺时针方向旋转至△A′B′C,
使点A′落在BC的延长线上.已知∠A=27°,∠B=40°,
则∠ACB′=____度.
46
8.(鞍山中考)如图,在△ABC中,∠ACB=90°,AC=4,BC=3,
将△ABC绕点A顺时针旋转得到△ADE(其中点B恰好落在AC延长线上点D处,点C落在点E处),连接BD,则四边形AEDB的面积为____.
9.(大连中考)如图,将△ABC绕点B逆时针旋转α,得到△EBD,
若点A恰好在ED的延长线上,则∠CAD的度数为( )
A.90°-α B.α
C.180°-α D.2α
C
D
C
12.如图,△ABC是等边三角形,点D是BC上的一点,
△ABD按逆时针方向旋转后到达△ACP的位置.
(1)旋转中心是点A;
(2)旋转角的度数为60°;
(3)求证:△ADP是等边三角形.
证明:∵由旋转的性质知PA=DA,
且旋转角∠DAP=∠BAC=60°,∴△ADP是等边三角形
13.如图,已知正方形ABCD中的△DCF可以经过旋转得到△BCE.
(1)图中哪一个点是旋转中心?△DCF按什么方向旋转了多少度?
(2)如果CF=3 cm,连接EF,求EF的长.
14.如图,在△ABC中,∠ACB=90°,∠B=30°,
以点C为旋转中心,将△ABC旋转到△A′B′C的位置,
使A′B′经过点A.
(1)求∠ACA′的度数;
(2)求线段AC与线段A′B′的数量关系.
解:(1)∵∠ACB=90°,∠B=30°,∴∠BAC=60°,
由旋转的性质可知,CA=CA′,∠A′=∠BAC=60°,
∴△ACA′为等边三角形,∴∠ACA′=60°
15.(达州期末)△ABC和△EFG是两块完全重合的等边三角形纸片(如图①所示),O是AC(或EF)的中点,△ABC不动,将△EFG绕O点顺时针转α(0°<α°<120°).
(1)试分别说明α是多少度时,点F在△ABC外部、BC上、内部(不证明)
(2)当点F不在BC上时,在图②,图③两种情况下(设EF或延长线与BC交于P,EG与CA或延长线交于Q),分别写出OP与OQ的数量关系,并从图②,③中选一种情况给予证明.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
