2021-2022学年沪科版数学七年级下册:8.1幂的运算(第3课时)课件(共23张PPT)
文档属性
| 名称 | 2021-2022学年沪科版数学七年级下册:8.1幂的运算(第3课时)课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 340.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
8.1幂的运算
沪科版数学七年级下
第三课时
积 的 乘 方
2.幂的乘方性质用语言表达为
3.弄清同底数幂相乘与幂的乘方的区别:前者是指数___,后者是指数___.
1、幂的乘方计算法则
(条件是m、n是正整数)
幂的乘方,
底数不变,
指数相乘.
相乘
相加
知识回顾
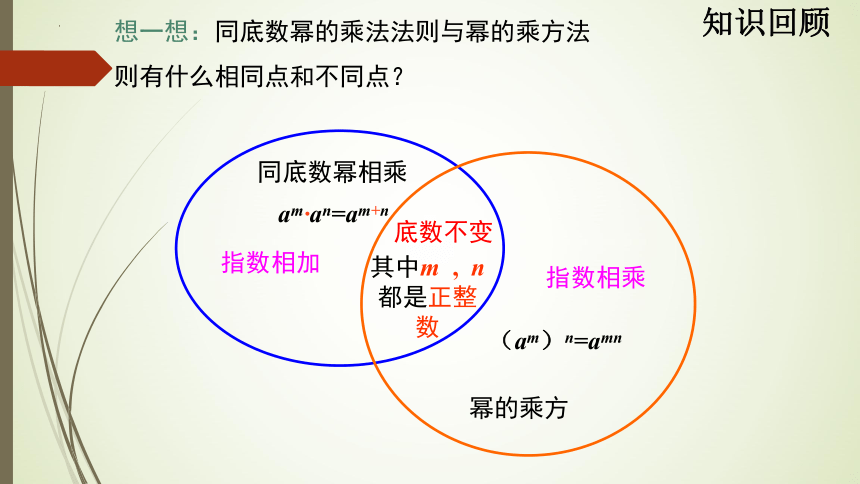
底数不变
指数相乘
指数相加
同底数幂相乘
幂的乘方
其中m , n都是正整数
(am)n=amn
am·an=am+n
想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?
知识回顾
4.计算:
(1)
(2)
(3)
(4)
(5)
(6)
知识回顾
解:
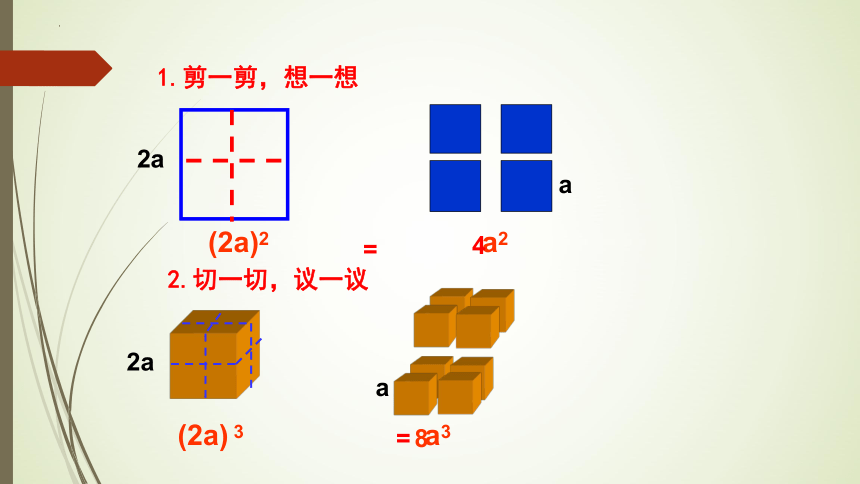
1.剪一剪,想一想
2.切一切,议一议
2a
(2a)2
a2
a
a3
(2a) 3
2a
a
4
=
8
=
同理:
(乘方的意义)
(乘法交换律、结合律)
(同底数幂相乘的法则)
(1)
(2)
观察、猜想
积的乘方
(ab)n =
思考:
猜想: (ab)n = (当m、n都是正整数)
即:
(乘方的意义)
(乘法结合律)
(乘方的意义)
an·bn
(ab)n = ab·ab·……·ab
=(a·a·……·a) (b·b·……·b)
=an·bn
n个ab
n个a
n个b
(ab)n = (n都是正整数)
an·bn
语言叙述:积的乘方,等于把积的每一因式分别乘方,再把所得的幂相乘.
语言表述:
积的乘方法则:积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
拓展:
当三个或三个以上因式的积乘方时, 也具有这一性质. 例如, (abc)n=anbncn
(ab)n=an bn
积的乘方公式:
例题解析
例1、计算:
(1)(3x)2 ; (2)(-2b)5 ; (3)(-2xy)4 ; (4)(3a2)n .
=32x2
= 9x2 ;
(1) (3x)2
解:
(2) (-2b)5
= (-2)5b5
= -32b5;
(3) (-2xy)4
= (-2x)4 y4
= (-2)4 x4 y4
(4) (3a2)n
= 3n (a2)n
= 3n a2n 。
=16x4 y4 ;
方法总结:运用积的乘方法则进行计算时,注意每个因式都要乘方,尤其是字母的系数不要漏乘方.
公式的反向使用
(ab)n = an·bn
(m,n都是正整数)
反向使用:
an·bn = (ab)n
试用简便方法计算:
(1) 23×53
(2) 28×58
= (2×5)3
= 103
= (2×5)8
= 108
(3) (-5)15 × (-2)15
(4) 24 × 44 ×(-0.125)4
= (-5)×[(-5)×(-2)]15
= -5×1015
= [2×4×(-0.125)]4
= 14
= 1 .
逆用公式即
(1)
解:原式=
2
2
(2)
解:原式= =
= =
2003
2003
例题解析
例2、木星是太阳系八大行星中最大的一颗。木星可以近似地看做是球体,它的半径约为7×104 千米,求木星的体积(结果精确到1014位, π取3.14)
解:
=
×(7×104)3
=
×
73×1012
≈
1.4×1015
(千米3)
注意
运算顺序 !
即它的体积大约是 1.4×1015 立方千米
×
√
×
×
(1)(3cd)3=9c3d3;
(2)(-3a3)2= -9a6;
(4)(-2x3y)3= -8x6y3;
(3)(a3+b2)3=a9+b6
(5)(- ab2)2= a b4;
×
1、下面的计算对不 对?如果不对,怎样改正?
知识巩固
2、、口答:(1)(ab)6=( ) (2)(-a)3 = ( )
(3)(-2x)4 = ( ) (4)(ab)3 = ( )
(5)(-xy)7 = ( ) (6)(-3abc)2 =( )
(7)[(-5)3]2 =( ) (8)[(-t)5]3 =( )
3、下面的计算对不对?如果不对,应怎样改正?
(1)(ab2)2=ab4; (2)(3cd)3=9c3d3;
(3)(-3a3)2= -9a6; (4)(-x3y)3= - x6y3;
(5)(a3+b2)3=a9+b6
×
×
×
×
×
(1) (2a)3
(2) (-5b)3
(3) (xy2)2
(4) (-2x3)4
4、计算
解:(1)(2a)3 =23·a3=8a3
(2) (-5b)3 =(-5)3·b3=-125b3
(3) (xy2)2 =x2· (y2)2=x2y4
(4) (-2x3)4 =(-2)4· (x3)4 =16x12
(5) (-2xy) 4
=(-2)4x4y4
(5)(-2xy)4
=16x4y4
能力提升
二、计算:
一、脱口而出:
(1) a6y3=( )3; (2)81x4y10=( )2
解:(1)
(2)(3xy2)2+(-xy3)·(-4xy)
=9x2y4+4x2y4
=13x2y4
整式的混合运算的关键:①理清运算顺序;
②用准法则。
能力提升
(1)
三、 计算
(2)(3xy2)2+(-xy3)·(-4xy)
{
幂的意义:
a·a· … ·a
n个a
an
=
同底数幂的乘法运算法则:
am · an=am+n
积的乘方运算法则: (ab)n=anbn
积的乘方=
反向使用am · an =am+n、(am)n =amn 可使某些计算简捷。
每个因式分别乘方后的积
{
幂的乘方(am)n =amn
拓展练习
(3)若x3= -8a6b9,则x=______
(1)若(a2b3 )n+1 = a6b3m,那么m+n=____
1、填空题:
(2) 如果(-3x y ) = ax y ,则a= , n= .
3
n
2
6
8
(4) 2x4y8 = ( )2
- 2a2b3
5
9
4
x2y4
拓展练习
2、已知x+2y-3=0, 求(2x×4y)2的值?
解:
(2x ×4y)2
=(2x) ×(4y)2
=22x ×42y
=22x ×(2 )2y
=22x ×(24y)
=22x+4y
∵x+2y-3=0
=22(x+2y)
∴x+2y=3
∴原式=22(x+2y)
=22×3
=26
=64
3、若Xa=2, xb=3, 求(x2a+b)2的值.
解:
(x2a+b)2
=
=
=
=×
=144
拓展练习
如何简便计算(0.04)2020×[(-5)2020]2
=(0.22)2020 × 54040
=(0.2)4040 × 54040
=(0.2 ×5)4040
=14040
(0.04)2020×[(-5)2020]2
=1.
解法一:
=(0.04)2020 × [(-5)2]2020
=(0.04×25)2020
=12020
=1.
= (0.04)2020 ×(25)2020
(0.04)2020×[(-5)2020]2
解法二:
拓展练习
8.1幂的运算
沪科版数学七年级下
第三课时
积 的 乘 方
2.幂的乘方性质用语言表达为
3.弄清同底数幂相乘与幂的乘方的区别:前者是指数___,后者是指数___.
1、幂的乘方计算法则
(条件是m、n是正整数)
幂的乘方,
底数不变,
指数相乘.
相乘
相加
知识回顾
底数不变
指数相乘
指数相加
同底数幂相乘
幂的乘方
其中m , n都是正整数
(am)n=amn
am·an=am+n
想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?
知识回顾
4.计算:
(1)
(2)
(3)
(4)
(5)
(6)
知识回顾
解:
1.剪一剪,想一想
2.切一切,议一议
2a
(2a)2
a2
a
a3
(2a) 3
2a
a
4
=
8
=
同理:
(乘方的意义)
(乘法交换律、结合律)
(同底数幂相乘的法则)
(1)
(2)
观察、猜想
积的乘方
(ab)n =
思考:
猜想: (ab)n = (当m、n都是正整数)
即:
(乘方的意义)
(乘法结合律)
(乘方的意义)
an·bn
(ab)n = ab·ab·……·ab
=(a·a·……·a) (b·b·……·b)
=an·bn
n个ab
n个a
n个b
(ab)n = (n都是正整数)
an·bn
语言叙述:积的乘方,等于把积的每一因式分别乘方,再把所得的幂相乘.
语言表述:
积的乘方法则:积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
拓展:
当三个或三个以上因式的积乘方时, 也具有这一性质. 例如, (abc)n=anbncn
(ab)n=an bn
积的乘方公式:
例题解析
例1、计算:
(1)(3x)2 ; (2)(-2b)5 ; (3)(-2xy)4 ; (4)(3a2)n .
=32x2
= 9x2 ;
(1) (3x)2
解:
(2) (-2b)5
= (-2)5b5
= -32b5;
(3) (-2xy)4
= (-2x)4 y4
= (-2)4 x4 y4
(4) (3a2)n
= 3n (a2)n
= 3n a2n 。
=16x4 y4 ;
方法总结:运用积的乘方法则进行计算时,注意每个因式都要乘方,尤其是字母的系数不要漏乘方.
公式的反向使用
(ab)n = an·bn
(m,n都是正整数)
反向使用:
an·bn = (ab)n
试用简便方法计算:
(1) 23×53
(2) 28×58
= (2×5)3
= 103
= (2×5)8
= 108
(3) (-5)15 × (-2)15
(4) 24 × 44 ×(-0.125)4
= (-5)×[(-5)×(-2)]15
= -5×1015
= [2×4×(-0.125)]4
= 14
= 1 .
逆用公式即
(1)
解:原式=
2
2
(2)
解:原式= =
= =
2003
2003
例题解析
例2、木星是太阳系八大行星中最大的一颗。木星可以近似地看做是球体,它的半径约为7×104 千米,求木星的体积(结果精确到1014位, π取3.14)
解:
=
×(7×104)3
=
×
73×1012
≈
1.4×1015
(千米3)
注意
运算顺序 !
即它的体积大约是 1.4×1015 立方千米
×
√
×
×
(1)(3cd)3=9c3d3;
(2)(-3a3)2= -9a6;
(4)(-2x3y)3= -8x6y3;
(3)(a3+b2)3=a9+b6
(5)(- ab2)2= a b4;
×
1、下面的计算对不 对?如果不对,怎样改正?
知识巩固
2、、口答:(1)(ab)6=( ) (2)(-a)3 = ( )
(3)(-2x)4 = ( ) (4)(ab)3 = ( )
(5)(-xy)7 = ( ) (6)(-3abc)2 =( )
(7)[(-5)3]2 =( ) (8)[(-t)5]3 =( )
3、下面的计算对不对?如果不对,应怎样改正?
(1)(ab2)2=ab4; (2)(3cd)3=9c3d3;
(3)(-3a3)2= -9a6; (4)(-x3y)3= - x6y3;
(5)(a3+b2)3=a9+b6
×
×
×
×
×
(1) (2a)3
(2) (-5b)3
(3) (xy2)2
(4) (-2x3)4
4、计算
解:(1)(2a)3 =23·a3=8a3
(2) (-5b)3 =(-5)3·b3=-125b3
(3) (xy2)2 =x2· (y2)2=x2y4
(4) (-2x3)4 =(-2)4· (x3)4 =16x12
(5) (-2xy) 4
=(-2)4x4y4
(5)(-2xy)4
=16x4y4
能力提升
二、计算:
一、脱口而出:
(1) a6y3=( )3; (2)81x4y10=( )2
解:(1)
(2)(3xy2)2+(-xy3)·(-4xy)
=9x2y4+4x2y4
=13x2y4
整式的混合运算的关键:①理清运算顺序;
②用准法则。
能力提升
(1)
三、 计算
(2)(3xy2)2+(-xy3)·(-4xy)
{
幂的意义:
a·a· … ·a
n个a
an
=
同底数幂的乘法运算法则:
am · an=am+n
积的乘方运算法则: (ab)n=anbn
积的乘方=
反向使用am · an =am+n、(am)n =amn 可使某些计算简捷。
每个因式分别乘方后的积
{
幂的乘方(am)n =amn
拓展练习
(3)若x3= -8a6b9,则x=______
(1)若(a2b3 )n+1 = a6b3m,那么m+n=____
1、填空题:
(2) 如果(-3x y ) = ax y ,则a= , n= .
3
n
2
6
8
(4) 2x4y8 = ( )2
- 2a2b3
5
9
4
x2y4
拓展练习
2、已知x+2y-3=0, 求(2x×4y)2的值?
解:
(2x ×4y)2
=(2x) ×(4y)2
=22x ×42y
=22x ×(2 )2y
=22x ×(24y)
=22x+4y
∵x+2y-3=0
=22(x+2y)
∴x+2y=3
∴原式=22(x+2y)
=22×3
=26
=64
3、若Xa=2, xb=3, 求(x2a+b)2的值.
解:
(x2a+b)2
=
=
=
=×
=144
拓展练习
如何简便计算(0.04)2020×[(-5)2020]2
=(0.22)2020 × 54040
=(0.2)4040 × 54040
=(0.2 ×5)4040
=14040
(0.04)2020×[(-5)2020]2
=1.
解法一:
=(0.04)2020 × [(-5)2]2020
=(0.04×25)2020
=12020
=1.
= (0.04)2020 ×(25)2020
(0.04)2020×[(-5)2020]2
解法二:
拓展练习
