2021-2022学年沪科版数学七年级下册8.1幂的运算(第4课时)课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年沪科版数学七年级下册8.1幂的运算(第4课时)课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 411.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
同底数幂的除法
8.1 幂 的 运 算
沪科版数学七年级下
第四课时
知识回顾
幂的乘方:
(am)n = amn ( m,n 都是正整数 ).
(ab)n=an bn ( m,n 都是正整数 )
积的乘方:
同底数幂的乘法:
=
(1) 2(x3)2·x3-(3x3)3+(5x)2·x7;
(2)(3xy2)2+(-4xy3) · (-xy) ;
(3)(-2x3)3·(x2)2.
解:原式=2x6·x3-27x9+25x2·x7
= 2x9-27x9+25x9 = 0;
解:原式=9x2y4 +4x2y4
=13x2y4;
解:原式= -8x9·x4 =-8x13.
1、计算:
回顾练习
2.如果(an bm b)3=a9b15,求m, n的值.
(an)3 (bm)3 b3=a9b15,
a 3n b 3m b3=a9b15 ,
a 3n b 3m+3=a9b15,
3n=9 ,3m+3=15.
n=3,m=4.
解:∵(an bm b)3=a9b15,
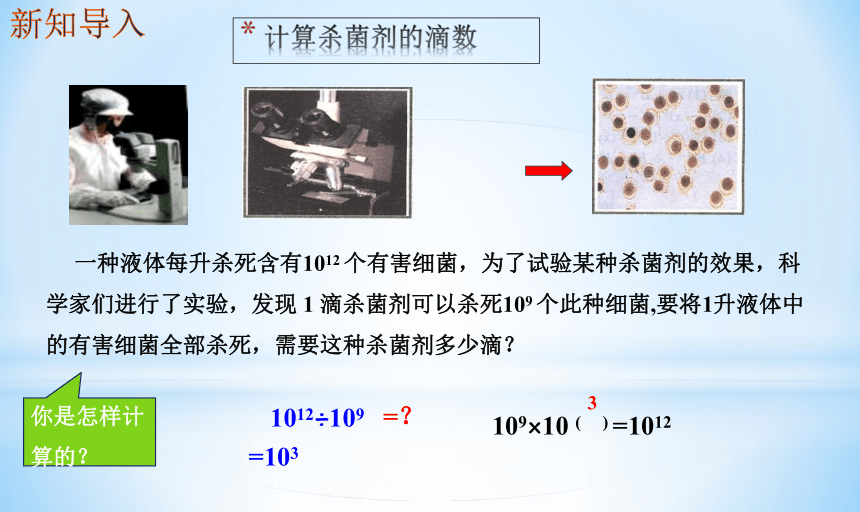
计算杀菌剂的滴数
一种液体每升杀死含有1012 个有害细菌,为了试验某种杀菌剂的效果,科学家们进行了实验,发现 1 滴杀菌剂可以杀死109 个此种细菌,要将1升液体中的有害细菌全部杀死,需要这种杀菌剂多少滴?
新知导入
你是怎样计算的?
1012÷109
109×10 ( ) =1012
=?
3
=103
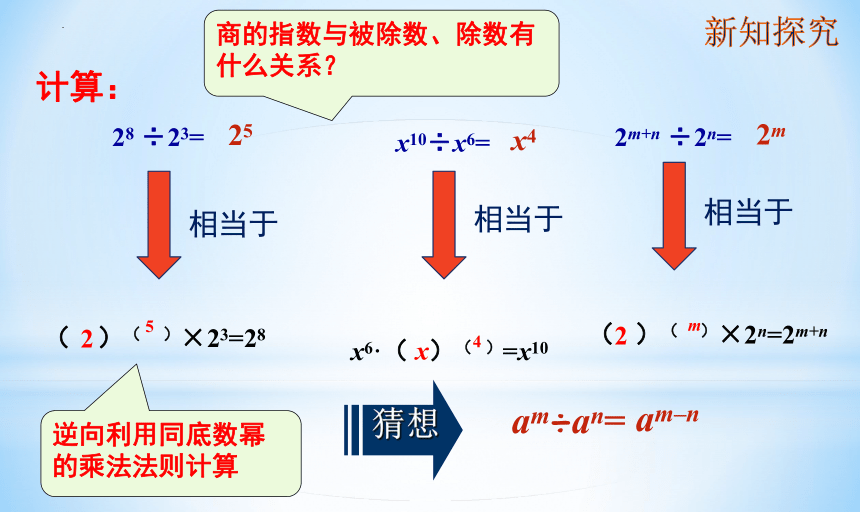
28 ÷23=
新知探究
计算:
x10÷x6=
2m+n ÷2n=
( )( )×23=28
x6·( )( )=x10
( )( )×2n=2m+n
2
5
x
4
2
m
相当于
相当于
相当于
逆向利用同底数幂的乘法法则计算
25
x4
2m
猜想
am÷an=
am–n
商的指数与被除数、除数有什么关系?
同底数幂相除,底数不变,指数相减.
同底幂的除法运算法则:
新知讲解
一般地,设m、n为正整数,m>n,a≠ 0 , 有
am÷an=
=am-n
同底数幂相除法则中各这字母必须满足什么条件?
a ÷ a =
(a≠0,m,n都是正整数,且m>n)
m
n
a
m-n
同底数幂相除,底数_____,指数______.
不变
相减
不要把 x 的指数误认为是0.
(1)运用法则的关键是看底数是否相同;
(2)因为零不能作除数,所以底数不能为0;
(3)注意单个字母的指数为1
同底数幂除法注意事项:
(1)
(2)
(3)
(4)
知识巩固
例1 计算
解:
(2)
(1)
底数有负号要加括号,最后要化简
(3)
(4)
÷ x
=
=
积的乘方要继续计算
不要把 x 的指数误认为是0
例3 计算
解:
计算:
(1)(-xy)13÷(-xy)8;
(2)(x-2y)3÷(2y-x)2;
(3)(a2+1)6÷(a2+1)4÷(a2+1)2.
课堂练习1
(3)原式=(a2+1)6-4-2=(a2+1)0=1.
解:(1)原式=(-xy)13-8=(-xy)5=-x5y5;
(2)原式=(x-2y)3÷(x-2y)2=x-2y;
已知am=12,an=2,a=3,求am-n-1的值.
方法总结:
解此题的关键是逆用同底数幂的除法,对am-n-1进行变形,再代入数值进行计算.
解:∵am=12,an=2,a=3,
∴am-n-1=am÷an÷a=12÷2÷3=2.
课堂练习2
计算:
提升练习2
解:(1)
(2)
底数不同利用幂的乘方性质改为同底数幂
1、已知:am=3,an=5. 求:
am-n的值 (2)a3m-2n的值
解:(1) am-n
= am ÷ an
= 3 ÷5
= 0.6
(2) a3m-2n= a 3m ÷ a 2n
= (am)3 ÷(an)2
=33 ÷52
=27 ÷25
=
拓展练习
拓展练习
已知 2x-5y-4=0,求4x÷32y的值
解:
4x÷32y
=
=
=
∵2x-5y-4=0
∴2x-5y=4
∴原式==16
=
幂的意义:
a·a· … ·a
n个a
an
同底数幂的乘法运算法则:
am · an =am+n
同底幂的除法运算法则:
am÷an=am–n
1.同底数幂相除的法则:
2.注意a≠0,m,n都是正整数,且m>n.
3.幂的四个运算法则:
同底数幂相乘:指数相加。
幂的乘方:指数相乘。
积的乘方:
同底数幂相除:指数相减。
幂的运算法则
最后结果中幂的形式应是最简的.
① 幂的指数、底数都应是最简的;
③ 幂的底数是积的形式时,要再用一次 (ab)n=an bn.
② 底数中系数不能为负;
注 意
同底数幂的除法
8.1 幂 的 运 算
沪科版数学七年级下
第四课时
知识回顾
幂的乘方:
(am)n = amn ( m,n 都是正整数 ).
(ab)n=an bn ( m,n 都是正整数 )
积的乘方:
同底数幂的乘法:
=
(1) 2(x3)2·x3-(3x3)3+(5x)2·x7;
(2)(3xy2)2+(-4xy3) · (-xy) ;
(3)(-2x3)3·(x2)2.
解:原式=2x6·x3-27x9+25x2·x7
= 2x9-27x9+25x9 = 0;
解:原式=9x2y4 +4x2y4
=13x2y4;
解:原式= -8x9·x4 =-8x13.
1、计算:
回顾练习
2.如果(an bm b)3=a9b15,求m, n的值.
(an)3 (bm)3 b3=a9b15,
a 3n b 3m b3=a9b15 ,
a 3n b 3m+3=a9b15,
3n=9 ,3m+3=15.
n=3,m=4.
解:∵(an bm b)3=a9b15,
计算杀菌剂的滴数
一种液体每升杀死含有1012 个有害细菌,为了试验某种杀菌剂的效果,科学家们进行了实验,发现 1 滴杀菌剂可以杀死109 个此种细菌,要将1升液体中的有害细菌全部杀死,需要这种杀菌剂多少滴?
新知导入
你是怎样计算的?
1012÷109
109×10 ( ) =1012
=?
3
=103
28 ÷23=
新知探究
计算:
x10÷x6=
2m+n ÷2n=
( )( )×23=28
x6·( )( )=x10
( )( )×2n=2m+n
2
5
x
4
2
m
相当于
相当于
相当于
逆向利用同底数幂的乘法法则计算
25
x4
2m
猜想
am÷an=
am–n
商的指数与被除数、除数有什么关系?
同底数幂相除,底数不变,指数相减.
同底幂的除法运算法则:
新知讲解
一般地,设m、n为正整数,m>n,a≠ 0 , 有
am÷an=
=am-n
同底数幂相除法则中各这字母必须满足什么条件?
a ÷ a =
(a≠0,m,n都是正整数,且m>n)
m
n
a
m-n
同底数幂相除,底数_____,指数______.
不变
相减
不要把 x 的指数误认为是0.
(1)运用法则的关键是看底数是否相同;
(2)因为零不能作除数,所以底数不能为0;
(3)注意单个字母的指数为1
同底数幂除法注意事项:
(1)
(2)
(3)
(4)
知识巩固
例1 计算
解:
(2)
(1)
底数有负号要加括号,最后要化简
(3)
(4)
÷ x
=
=
积的乘方要继续计算
不要把 x 的指数误认为是0
例3 计算
解:
计算:
(1)(-xy)13÷(-xy)8;
(2)(x-2y)3÷(2y-x)2;
(3)(a2+1)6÷(a2+1)4÷(a2+1)2.
课堂练习1
(3)原式=(a2+1)6-4-2=(a2+1)0=1.
解:(1)原式=(-xy)13-8=(-xy)5=-x5y5;
(2)原式=(x-2y)3÷(x-2y)2=x-2y;
已知am=12,an=2,a=3,求am-n-1的值.
方法总结:
解此题的关键是逆用同底数幂的除法,对am-n-1进行变形,再代入数值进行计算.
解:∵am=12,an=2,a=3,
∴am-n-1=am÷an÷a=12÷2÷3=2.
课堂练习2
计算:
提升练习2
解:(1)
(2)
底数不同利用幂的乘方性质改为同底数幂
1、已知:am=3,an=5. 求:
am-n的值 (2)a3m-2n的值
解:(1) am-n
= am ÷ an
= 3 ÷5
= 0.6
(2) a3m-2n= a 3m ÷ a 2n
= (am)3 ÷(an)2
=33 ÷52
=27 ÷25
=
拓展练习
拓展练习
已知 2x-5y-4=0,求4x÷32y的值
解:
4x÷32y
=
=
=
∵2x-5y-4=0
∴2x-5y=4
∴原式==16
=
幂的意义:
a·a· … ·a
n个a
an
同底数幂的乘法运算法则:
am · an =am+n
同底幂的除法运算法则:
am÷an=am–n
1.同底数幂相除的法则:
2.注意a≠0,m,n都是正整数,且m>n.
3.幂的四个运算法则:
同底数幂相乘:指数相加。
幂的乘方:指数相乘。
积的乘方:
同底数幂相除:指数相减。
幂的运算法则
最后结果中幂的形式应是最简的.
① 幂的指数、底数都应是最简的;
③ 幂的底数是积的形式时,要再用一次 (ab)n=an bn.
② 底数中系数不能为负;
注 意
