2021-2022学年七年级数学下学期沪科版8.3完全平方公式与平方差公式(第2课时,平方差公式)(共31张ppt)课件
文档属性
| 名称 | 2021-2022学年七年级数学下学期沪科版8.3完全平方公式与平方差公式(第2课时,平方差公式)(共31张ppt)课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 438.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 00:00:00 | ||
图片预览


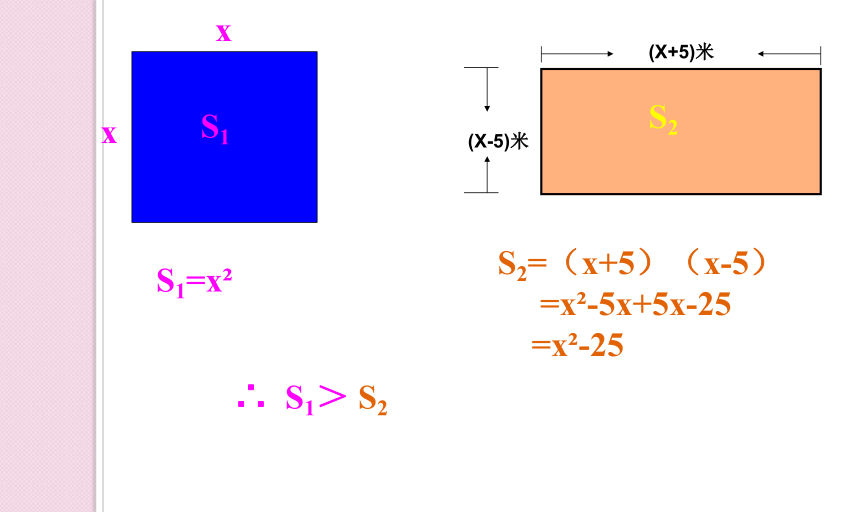



文档简介
(共31张PPT)
第2课时 平方差公式
8.3完全平方公式与平方差公式
沪科版七年级下册
a
b
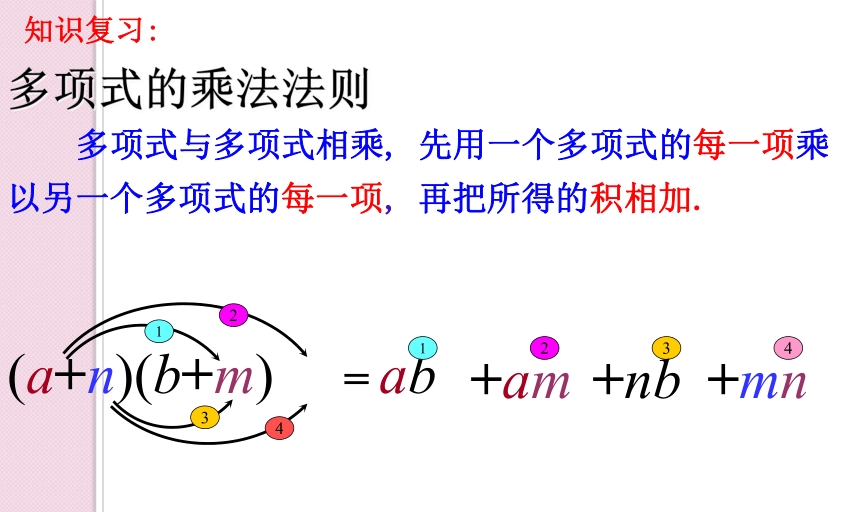
(a+n)(b+m)
=
ab
1
2
3
4
+am
+nb
+mn
多项式的乘法法则
1
2
3
4
多项式与多项式相乘, 先用一个多项式的每一项乘以另一个多项式的每一项, 再把所得的积相加.
知识复习:
知识回顾
2. 想一想:
(1)两个公式中的字母都能表示什么
(2)完全平方公式在计算化简中有些什么作用
(3)根据两数和或差的完全平方公式,能够计算多个数的和或差的平方吗
1.
(a+b) 2=a2+2ab+b2
(a-b) 2=a2-2ab+b2
完全平方公式:
5米
5米
x 米
(X-5)米
(X+5)米
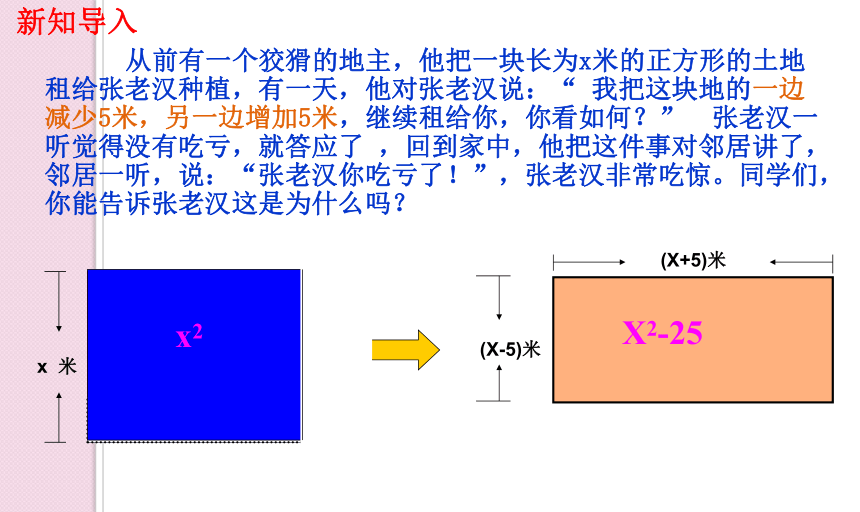
x2
X2-25
新知导入
从前有一个狡猾的地主,他把一块长为x米的正方形的土地租给张老汉种植,有一天,他对张老汉说:“ 我把这块地的一边减少5米,另一边增加5米,继续租给你,你看如何?” 张老汉一听觉得没有吃亏,就答应了 ,回到家中,他把这件事对邻居讲了,邻居一听,说:“张老汉你吃亏了!”,张老汉非常吃惊。同学们,你能告诉张老汉这是为什么吗?
x
(X-5)米
(X+5)米
x
S1
S2
S1=x
S2=(x+5)(x-5)
=x -5x+5x-25
=x -25
∴ S1> S2
计算下列多项式的积:
(x+1)(x-1) =
(m+2)(m-2) =
(2x+1)(2x-1) =
x2 - 1
m2 - 4
4x2 - 1
算式有什么结构特征?
结果有什么结构特征?
两项的和乘以两项的差
结果是两项平方差
新知讲解
验证:
(a+b)(a-b)
= a2-ab+ab-b2
= a2-b2
合并同类项
(a+b)(a-b)
= a2-b2
(a+b)(a-b)=a2-b2
两个数的和 乘以这两个数的差,等于这两个数的平方差。
平方差公式
新知讲解
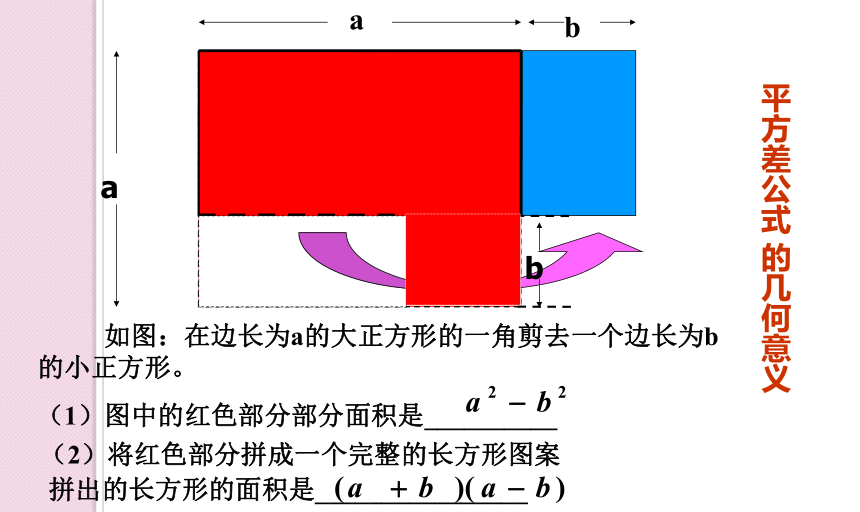
拼出的长方形的面积是________________
a
b
a
b
如图:在边长为a的大正方形的一角剪去一个边长为b的小正方形。
(1)图中的红色部分部分面积是__________
(2)将红色部分拼成一个完整的长方形图案
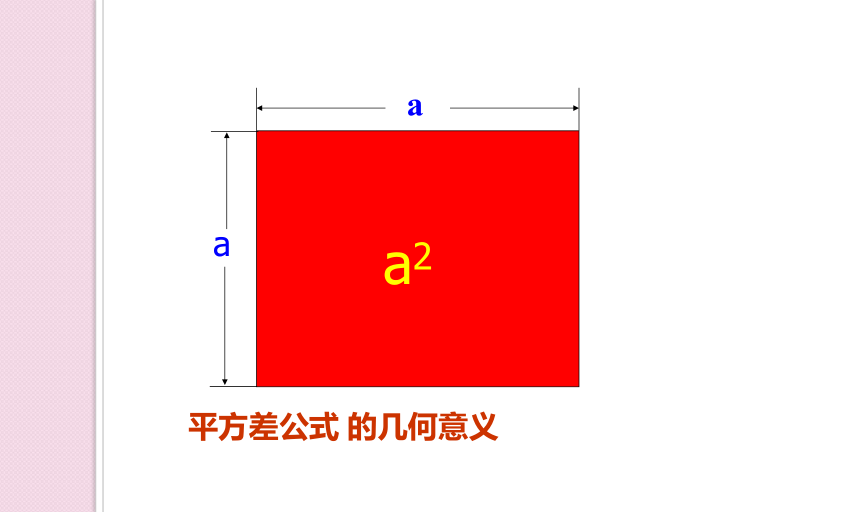
平方差公式 的几何意义
a
a
a2
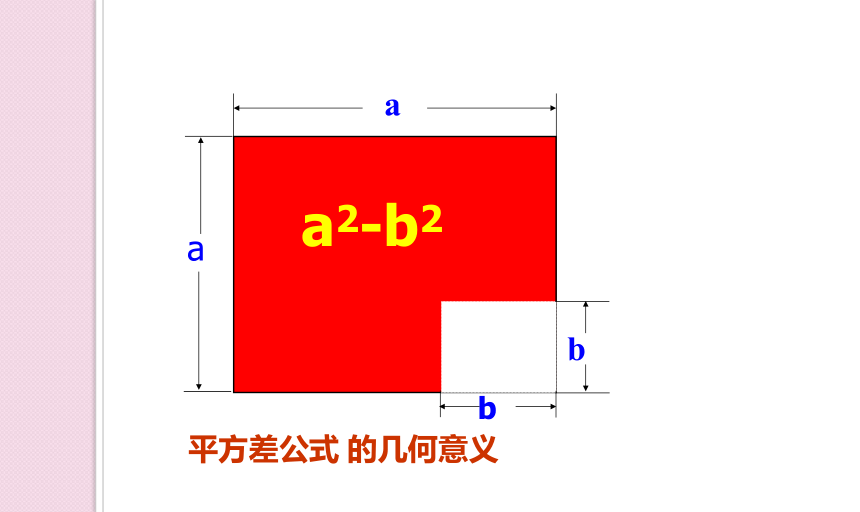
平方差公式 的几何意义
b
a
a2-b2
a
b
平方差公式 的几何意义
b
a
a
b
1
2
(a+b)(a-b)
1
2
(a+b)(a-b)
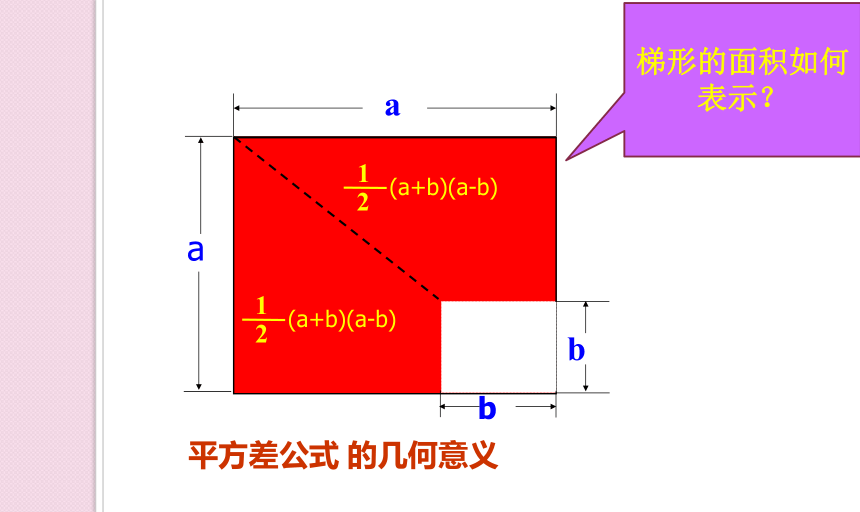
平方差公式 的几何意义
梯形的面积如何表示?
b
a
a
b
(a+b)(a-b)
(a+b)(a-b)=a2-b2
两个梯形面积和是多少?
(a + b) ( a - b) = a2 - b2
特征:
两数的和
两数的差
这两数的平方差
(a+b)(a-b)=a2-b2
特征:
两个二项式相乘
(a + b) (a - b) = a2-b2
公式特征:
符号相同项
符号相反项
两个二项式相乘
两项平方差
(相同项)2-(相反项)2
概括总结
(2)等号右边是乘式中两项的平方差.
(相同项)2-(相反项)2
平方差公式的特征:
(1)等号左边是两个二项式相乘.一项相同,一项互为相反数.
注意:
公式中的字母的意义很广泛,可以代表常数,单项式或多项式 .
(l)(-a+b)(a+b)= _________
(2)(a-b)(b+a)= __________
(3)(-a-b)(-a+b)= ________
(4)(a-b)(-a-b)= _________
a2-b2
a2-b2
b2-a2
b2-a2
(a+b)(a b)=
a2 b2
用平方差公式直接计算下列各式
讨论:利用平方差公式计算的关键是__________
怎样确定a与b:______________________
准确确定a和b
符号相同的项是a,符号相反的项是b
公式解析
(相同项)2-(相反项)2
下列式子中哪些可以用平方差公式运算
(1) (-4k+3)(-4k-3) (2) (1-x)(-x-1)
(3) (-x-1)(x+1) (4)(x+3)(x-2)
不可以
可以
可以
不可以
公式解析
例1、运用平方差公式填空:
1、(m+n)(-n+m) =
2、(-x-y) (x-y) =
3、(2a+b)(2a-b) =
4、(x2+y2)(x2-y2)=
5、 51 × 49 =
m2-n2
位置变化
y2-x2
符号变化
4a2-b2
系数变化
x4-y4
指数变化
2499
无中生有
(a+b)(a-b)=a2-b2
例2、简便计算
⑴ 102×98
⑵ 50 ×49
⑶ 59.8×60.2
⑷ 5678×5680-56792
解:
⑴ 102×98
=(100+2)×(100-2)
=100 -4
= 9996
⑷ 5678×5680-56792
=(5679-1)×(5679+1)-5679
=5679 -1-5679
⑵ 50 ×49
= (50+ )×(50- )
=2500- =2499
⑶ 59.8×60.2
=(60-0.2)×(60+0.2)
=3600-0.04=3599.96
例3、(a+b-c)(a-b-c)能用平方差公式运算吗 若能结果是哪两数的平方差
解:原式=[(a-c)+b][(a-c)-b]
=(a-c)2-b2
=a2-2ac+c2-b2
三项式重组为两项的和与差
重组方法:
[(前后同号项)+(前后异号项)][(前后同号项)-(前后异号项)]
判断并改错:
(1) (a+3)(a-3)=a -3 ( )
改正:
(2)(5y+2)(5y-2)=5y -4 ( )
改正:
(3) (1- 4xy)(-1- 4xy)=1-16x y ( )
改正:
(4)(-ab+3c)(-3c-ab)=a b -9c ( )
改正:
(5) (-m+7)(7-m)=m -49 ( )
改正:
×
×
×
×
√
(a+3)(a-3)=a -9
(5y+2)(5y-2)=25y -4
原式=(- 4xy+1)(- 4xy-1)=16x y -1
(-m+7)(7-m)=(7-m)(7-m)=(7-m)
课堂练习
⑴ (a+1)(a-1)=
⑵ (3+x)(3-x)=
⑶ (a+2b)(a-2b)=
⑷ (3x+5y)(3x-5y)=
⑸ (10s-3t)(10s+3t)=
⑹ (-m+n)(-m-n)=
a2-1
9-x2
a2-(2b)2
=a2-4b2
(3x)2-(5y)2
=9x2-25y2
(10s)2-(3t)2
=100s2-9t2
(-m)2-n2
=m2-n2
运用平方差公式计算:
课堂练习
⑺ (-2x-3y) (-2x+3y)=
⑽ (-4x+y)(y+4x)=
(-2x)2-(3y)2
y2-(4x)2
=y2-16x2
=4x2-9y2
= a2-4b2
( a)2-(2b)2
⑻ ( a-2b)(2b+ a)=
⑼ (b+a)(- b+a)=
a2-( b)2
= a2- b2
课堂练习
1、某同学化简a(a+2b)﹣(a+b)(a﹣b)出现了错误,解答过程如下:
原式=a2+2ab﹣(a2﹣b2) (第一步)
=a2+2ab﹣a2﹣b2(第二步)
=2ab﹣b2 (第三步)
(1)该同学解答过程从第 步开始出错,
错误原因是 ;
提升练习
二
去括号时没有变号
解:原式=a2+2ab﹣(a2﹣b2)
=a2+2ab﹣a2+b2
=2ab+b2.
(2)写出此题正确的解答过程.
提升练习
2、先化简在求值,(2x+3)2﹣(2x+3)(2x﹣3)其中x= - 2
(2x+3)2﹣(2x+3)(2x﹣3)
=(2x)2+12x+9﹣[(2x2)﹣9]
=(2x)2+12x+9﹣(2x)2+9
=12x+18
解:
当x= - 2时
原式=12x+18=12×(-2)+18=-6
3、先化简,再求值:x(x+1)+(2+x)(2﹣x),其中x=-4
原式=-4 +4=
.
解:x(x+1)+(2+x)(2﹣x)
=x2+x+4﹣x2
=x+4,
当x=-4时
计算
拓展练习
拓展练习
求(2+1)(22+1)(24+1)(28+1) )(216+1)(232+1)+1的个位数字
解:原式=(2-1)(2+1)(22+1)(24+1)(28+1) )(216+1)(232+1)+1
=(24-1)(24+1)(28+1) )(216+1)(232+1)+1
=264-1+1
=232
∵21=2,22=4,23=8,24=16,个位数字按照2,4,8,6依次循环
而64=4×16
∴原式的个位数字是6
小 结
(a+b)(a-b)=
a2
- b2
两数和与这两数差的积,等于它们的平方差
注意
1)左边为两个数的和与差的积,右边为两个数的平方差
2)有些式子通过适当变形可以用公式
3)公式中的a和b可以是数,也可以是整式
4)最后结果必须化简
第2课时 平方差公式
8.3完全平方公式与平方差公式
沪科版七年级下册
a
b
(a+n)(b+m)
=
ab
1
2
3
4
+am
+nb
+mn
多项式的乘法法则
1
2
3
4
多项式与多项式相乘, 先用一个多项式的每一项乘以另一个多项式的每一项, 再把所得的积相加.
知识复习:
知识回顾
2. 想一想:
(1)两个公式中的字母都能表示什么
(2)完全平方公式在计算化简中有些什么作用
(3)根据两数和或差的完全平方公式,能够计算多个数的和或差的平方吗
1.
(a+b) 2=a2+2ab+b2
(a-b) 2=a2-2ab+b2
完全平方公式:
5米
5米
x 米
(X-5)米
(X+5)米
x2
X2-25
新知导入
从前有一个狡猾的地主,他把一块长为x米的正方形的土地租给张老汉种植,有一天,他对张老汉说:“ 我把这块地的一边减少5米,另一边增加5米,继续租给你,你看如何?” 张老汉一听觉得没有吃亏,就答应了 ,回到家中,他把这件事对邻居讲了,邻居一听,说:“张老汉你吃亏了!”,张老汉非常吃惊。同学们,你能告诉张老汉这是为什么吗?
x
(X-5)米
(X+5)米
x
S1
S2
S1=x
S2=(x+5)(x-5)
=x -5x+5x-25
=x -25
∴ S1> S2
计算下列多项式的积:
(x+1)(x-1) =
(m+2)(m-2) =
(2x+1)(2x-1) =
x2 - 1
m2 - 4
4x2 - 1
算式有什么结构特征?
结果有什么结构特征?
两项的和乘以两项的差
结果是两项平方差
新知讲解
验证:
(a+b)(a-b)
= a2-ab+ab-b2
= a2-b2
合并同类项
(a+b)(a-b)
= a2-b2
(a+b)(a-b)=a2-b2
两个数的和 乘以这两个数的差,等于这两个数的平方差。
平方差公式
新知讲解
拼出的长方形的面积是________________
a
b
a
b
如图:在边长为a的大正方形的一角剪去一个边长为b的小正方形。
(1)图中的红色部分部分面积是__________
(2)将红色部分拼成一个完整的长方形图案
平方差公式 的几何意义
a
a
a2
平方差公式 的几何意义
b
a
a2-b2
a
b
平方差公式 的几何意义
b
a
a
b
1
2
(a+b)(a-b)
1
2
(a+b)(a-b)
平方差公式 的几何意义
梯形的面积如何表示?
b
a
a
b
(a+b)(a-b)
(a+b)(a-b)=a2-b2
两个梯形面积和是多少?
(a + b) ( a - b) = a2 - b2
特征:
两数的和
两数的差
这两数的平方差
(a+b)(a-b)=a2-b2
特征:
两个二项式相乘
(a + b) (a - b) = a2-b2
公式特征:
符号相同项
符号相反项
两个二项式相乘
两项平方差
(相同项)2-(相反项)2
概括总结
(2)等号右边是乘式中两项的平方差.
(相同项)2-(相反项)2
平方差公式的特征:
(1)等号左边是两个二项式相乘.一项相同,一项互为相反数.
注意:
公式中的字母的意义很广泛,可以代表常数,单项式或多项式 .
(l)(-a+b)(a+b)= _________
(2)(a-b)(b+a)= __________
(3)(-a-b)(-a+b)= ________
(4)(a-b)(-a-b)= _________
a2-b2
a2-b2
b2-a2
b2-a2
(a+b)(a b)=
a2 b2
用平方差公式直接计算下列各式
讨论:利用平方差公式计算的关键是__________
怎样确定a与b:______________________
准确确定a和b
符号相同的项是a,符号相反的项是b
公式解析
(相同项)2-(相反项)2
下列式子中哪些可以用平方差公式运算
(1) (-4k+3)(-4k-3) (2) (1-x)(-x-1)
(3) (-x-1)(x+1) (4)(x+3)(x-2)
不可以
可以
可以
不可以
公式解析
例1、运用平方差公式填空:
1、(m+n)(-n+m) =
2、(-x-y) (x-y) =
3、(2a+b)(2a-b) =
4、(x2+y2)(x2-y2)=
5、 51 × 49 =
m2-n2
位置变化
y2-x2
符号变化
4a2-b2
系数变化
x4-y4
指数变化
2499
无中生有
(a+b)(a-b)=a2-b2
例2、简便计算
⑴ 102×98
⑵ 50 ×49
⑶ 59.8×60.2
⑷ 5678×5680-56792
解:
⑴ 102×98
=(100+2)×(100-2)
=100 -4
= 9996
⑷ 5678×5680-56792
=(5679-1)×(5679+1)-5679
=5679 -1-5679
⑵ 50 ×49
= (50+ )×(50- )
=2500- =2499
⑶ 59.8×60.2
=(60-0.2)×(60+0.2)
=3600-0.04=3599.96
例3、(a+b-c)(a-b-c)能用平方差公式运算吗 若能结果是哪两数的平方差
解:原式=[(a-c)+b][(a-c)-b]
=(a-c)2-b2
=a2-2ac+c2-b2
三项式重组为两项的和与差
重组方法:
[(前后同号项)+(前后异号项)][(前后同号项)-(前后异号项)]
判断并改错:
(1) (a+3)(a-3)=a -3 ( )
改正:
(2)(5y+2)(5y-2)=5y -4 ( )
改正:
(3) (1- 4xy)(-1- 4xy)=1-16x y ( )
改正:
(4)(-ab+3c)(-3c-ab)=a b -9c ( )
改正:
(5) (-m+7)(7-m)=m -49 ( )
改正:
×
×
×
×
√
(a+3)(a-3)=a -9
(5y+2)(5y-2)=25y -4
原式=(- 4xy+1)(- 4xy-1)=16x y -1
(-m+7)(7-m)=(7-m)(7-m)=(7-m)
课堂练习
⑴ (a+1)(a-1)=
⑵ (3+x)(3-x)=
⑶ (a+2b)(a-2b)=
⑷ (3x+5y)(3x-5y)=
⑸ (10s-3t)(10s+3t)=
⑹ (-m+n)(-m-n)=
a2-1
9-x2
a2-(2b)2
=a2-4b2
(3x)2-(5y)2
=9x2-25y2
(10s)2-(3t)2
=100s2-9t2
(-m)2-n2
=m2-n2
运用平方差公式计算:
课堂练习
⑺ (-2x-3y) (-2x+3y)=
⑽ (-4x+y)(y+4x)=
(-2x)2-(3y)2
y2-(4x)2
=y2-16x2
=4x2-9y2
= a2-4b2
( a)2-(2b)2
⑻ ( a-2b)(2b+ a)=
⑼ (b+a)(- b+a)=
a2-( b)2
= a2- b2
课堂练习
1、某同学化简a(a+2b)﹣(a+b)(a﹣b)出现了错误,解答过程如下:
原式=a2+2ab﹣(a2﹣b2) (第一步)
=a2+2ab﹣a2﹣b2(第二步)
=2ab﹣b2 (第三步)
(1)该同学解答过程从第 步开始出错,
错误原因是 ;
提升练习
二
去括号时没有变号
解:原式=a2+2ab﹣(a2﹣b2)
=a2+2ab﹣a2+b2
=2ab+b2.
(2)写出此题正确的解答过程.
提升练习
2、先化简在求值,(2x+3)2﹣(2x+3)(2x﹣3)其中x= - 2
(2x+3)2﹣(2x+3)(2x﹣3)
=(2x)2+12x+9﹣[(2x2)﹣9]
=(2x)2+12x+9﹣(2x)2+9
=12x+18
解:
当x= - 2时
原式=12x+18=12×(-2)+18=-6
3、先化简,再求值:x(x+1)+(2+x)(2﹣x),其中x=-4
原式=-4 +4=
.
解:x(x+1)+(2+x)(2﹣x)
=x2+x+4﹣x2
=x+4,
当x=-4时
计算
拓展练习
拓展练习
求(2+1)(22+1)(24+1)(28+1) )(216+1)(232+1)+1的个位数字
解:原式=(2-1)(2+1)(22+1)(24+1)(28+1) )(216+1)(232+1)+1
=(24-1)(24+1)(28+1) )(216+1)(232+1)+1
=264-1+1
=232
∵21=2,22=4,23=8,24=16,个位数字按照2,4,8,6依次循环
而64=4×16
∴原式的个位数字是6
小 结
(a+b)(a-b)=
a2
- b2
两数和与这两数差的积,等于它们的平方差
注意
1)左边为两个数的和与差的积,右边为两个数的平方差
2)有些式子通过适当变形可以用公式
3)公式中的a和b可以是数,也可以是整式
4)最后结果必须化简
