九年级下册数学第三章圆单元测试一(有答案)
文档属性
| 名称 | 九年级下册数学第三章圆单元测试一(有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 202.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-20 00:00:00 | ||
图片预览


文档简介
九年级下册数学第三章圆单元测试一
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.已知两圆相外切,连心线长度是10厘米,其中一圆的半径为6厘米,则另一圆的半径是:
4厘米 6厘米 10厘米 16厘米
2.如图,等边△ABC的周长为6π,半径是1的⊙O从与AB相切于点D的位置
出发,在△ABC外部按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,则⊙O自转了:【 】
A.2周 B.3周 C.4周 D.5周
4.两个圆的半径分别为4cm和3cm,圆心距是7cm,则这两个圆的位置关系是( )
A.内切 B.相交 C.外切 D.外离
5.已知圆和圆相切,两圆的圆心距为8cm,圆的半径为3cm,则圆的半径是( ).
A.5cm B.11cm C.3cm D.5cm或11cm
6.如图,⊙O的直径CD⊥AB,∠AOC=50°,则∠CDB大小为 ( )
A.25° B.30° C.40° D.50°
7.两圆的半径分别为2和5,圆心距为7,则这两圆的位置关系为
(A)外离.(B)外切.(C)相交.(D)内切.
8.如图,⊙O是△ABC的外接圆,已知∠ABO=30o,则∠ACB的大小为 ( )
A. 60o B.30o C.45o D. 50o
9.在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙ A的半径为2,下列说法中不正确的是 ( )
A、当a<5时,点B在⊙A内 B、当1C、当a<1时,点B在⊙A外 D、当a>5时,点B在⊙A外
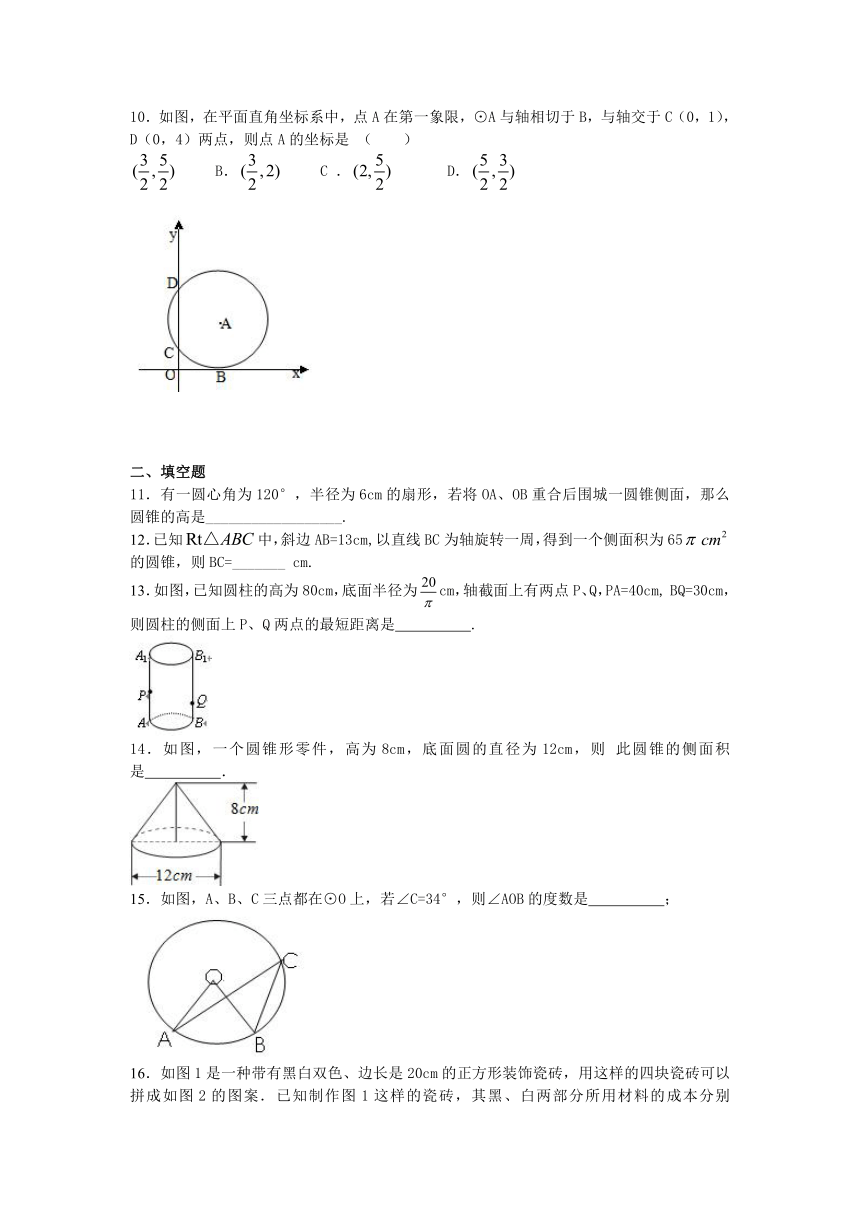
10.如图,在平面直角坐标系中,点A在第一象限,⊙A与轴相切于B,与轴交于C(0,1),D(0,4)两点,则点A的坐标是 ( )
B. C . D.
二、填空题
11.有一圆心角为120°,半径为6cm的扇形,若将OA、OB重合后围城一圆锥侧面,那么圆锥的高是__________________.
12.已知中,斜边AB=13cm,以直线BC为轴旋转一周,得到一个侧面积为65的圆锥,则BC=_______ cm.
13.如图,已知圆柱的高为80cm,底面半径为cm,轴截面上有两点P、Q,PA=40cm, BQ=30cm,则圆柱的侧面上P、Q两点的最短距离是 .
14.如图,一个圆锥形零件,高为8cm,底面圆的直径为12cm,则 此圆锥的侧面积是 .
15.如图,A、B、C三点都在⊙O上,若∠C=34°,则∠AOB的度数是 ;
16.如图1是一种带有黑白双色、边长是20cm的正方形装饰瓷砖,用这样的四块瓷砖可以拼成如图2的图案.已知制作图1这样的瓷砖,其黑、白两部分所用材料的成本分别
三、计算题
四、解答题
17.已知直角中,∠C=90°.
(1)请用直尺和圆规在图中画出直角的外接圆;(不写作法,保留作图痕迹)
(2)若AC=5,BC=12,请求出该直角的外接圆面积.
18.小明用一根铁丝围成了一个面积为25cm2的正方形,小颖对小明说:“我用这根铁丝可以围个面积也是25cm2的圆,且铁丝还有剩余”。问小颖能成功吗?若能,请估计可剩多少厘米的铁丝?(误差小于1cm)若不能,请说明理由。
19.如图,在△ABC中,∠BAC=30°,以AB为直径的⊙O经过点C.过点C作⊙O的切线交AB的延长线于点P.点D为圆上一点,且,弦AD的延长线交切线PC于点E,连接BC.
(1)判断OB和BP的数量关系,并说明理由;
(2)若⊙O的半径为2,求AE的长.
20.如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF,BF,求∠ABF的度数;
(3)如果CD=15,BE=10,sinA=,求⊙O的半径.
21.如图,已知为坐标原点,点的坐标为,的半径为1,过作直线平行于轴,点在上运动.
(1)当点运动到圆上时,求线段的长.
(2)当点的坐标为时,试判断直线与的位置关系,并说明理由.
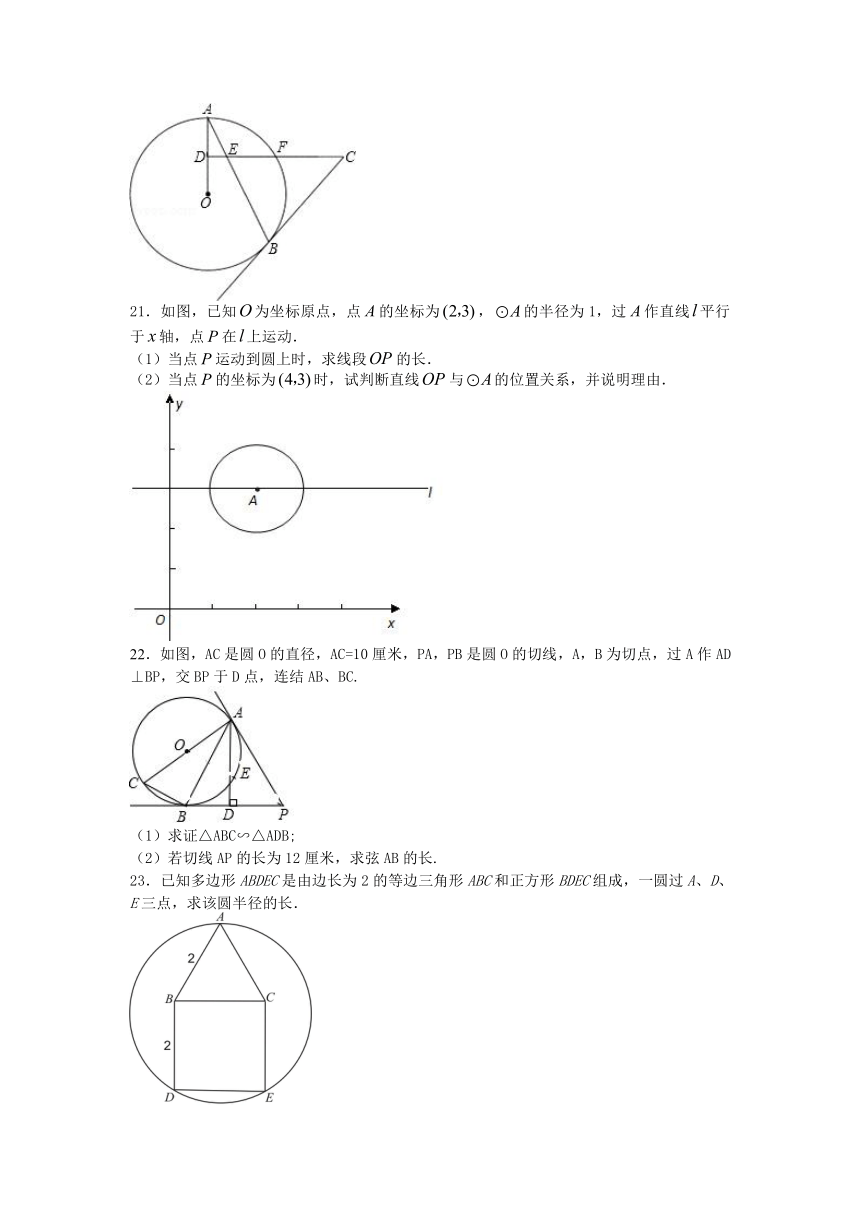
22.如图,AC是圆O的直径,AC=10厘米,PA,PB是圆O的切线,A,B为切点,过A作AD⊥BP,交BP于D点,连结AB、BC.
(1)求证△ABC∽△ADB;
(2)若切线AP的长为12厘米,求弦AB的长.
23.已知多边形ABDEC是由边长为2的等边三角形ABC和正方形BDEC组成,一圆过A、D、E三点,求该圆半径的长.
24.已知:如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.
求证:(1)△ABC是等边三角形;
(2).
25.已知等边△ABC和⊙M.
(1)如图l,若⊙M与BA的延长线AK及边AC均相切,求证: AM∥BC;
(2)如图2,若⊙M与BA的延长线AK、BC的延长线CF及边AC均相切,求证:四边形ABCM是平行四边形.
参考答案
1.A
2.C。
3. C
4.C
5.D
6.A
7.B
8.A
9.A
10.C
11.
12.12
13.
14.60πcm2。
15.68°
16.6.37
17.(1)略(2)
18.解:设正方形边长为a(cm),周长为c1(cm),圆的半径为R(cm),周长为c2(cm),
由R2=25得R=,∴c2=2R=2()=10=20.又∵,∴1719.(1)OB=BP,理由见解析(2)3
20.(1)略(2)30°(3)
21.解:(1)如图,设与轴交点为
当点运动到圆上时,有两个位置
,
(2)连接,过作,垂足为
,
在中,
,
直线与相离.
22.(1)证明:∵AC是圆O的直径,∴∠ABC=90 o,
又∵AD⊥BP,∴∠ADB=90 o,∴∠ABC=∠ADB,
又∵PB是圆的切线,∴∠ABD=∠ACB,
在△ABC和△ADB中:
,∴△ABC∽△ADB;
如图,连结OP,
在Rt△AOP中,AP=12厘米,OA=5厘米,根据勾股定理求得OP=13厘米,
又由已知可证得△ABC∽△PAO, ∴,得,解得AB=厘米.
23.2
24.证明:(1)连结OD得OD∥AC ∴∠BDO=∠A 又由OB=OD得∠OBD=∠ODB
∴∠OBD=∠A ∴BC=AC 又∵AB=AC ∴△ABC是等边三角形
(2)连结CD,则CD⊥AB ∴D是AB中点
∵AE=AD=AB ∴EC=3AE ∴.
25.略
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.已知两圆相外切,连心线长度是10厘米,其中一圆的半径为6厘米,则另一圆的半径是:
4厘米 6厘米 10厘米 16厘米
2.如图,等边△ABC的周长为6π,半径是1的⊙O从与AB相切于点D的位置
出发,在△ABC外部按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,则⊙O自转了:【 】
A.2周 B.3周 C.4周 D.5周
4.两个圆的半径分别为4cm和3cm,圆心距是7cm,则这两个圆的位置关系是( )
A.内切 B.相交 C.外切 D.外离
5.已知圆和圆相切,两圆的圆心距为8cm,圆的半径为3cm,则圆的半径是( ).
A.5cm B.11cm C.3cm D.5cm或11cm
6.如图,⊙O的直径CD⊥AB,∠AOC=50°,则∠CDB大小为 ( )
A.25° B.30° C.40° D.50°
7.两圆的半径分别为2和5,圆心距为7,则这两圆的位置关系为
(A)外离.(B)外切.(C)相交.(D)内切.
8.如图,⊙O是△ABC的外接圆,已知∠ABO=30o,则∠ACB的大小为 ( )
A. 60o B.30o C.45o D. 50o
9.在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙ A的半径为2,下列说法中不正确的是 ( )
A、当a<5时,点B在⊙A内 B、当1
10.如图,在平面直角坐标系中,点A在第一象限,⊙A与轴相切于B,与轴交于C(0,1),D(0,4)两点,则点A的坐标是 ( )
B. C . D.
二、填空题
11.有一圆心角为120°,半径为6cm的扇形,若将OA、OB重合后围城一圆锥侧面,那么圆锥的高是__________________.
12.已知中,斜边AB=13cm,以直线BC为轴旋转一周,得到一个侧面积为65的圆锥,则BC=_______ cm.
13.如图,已知圆柱的高为80cm,底面半径为cm,轴截面上有两点P、Q,PA=40cm, BQ=30cm,则圆柱的侧面上P、Q两点的最短距离是 .
14.如图,一个圆锥形零件,高为8cm,底面圆的直径为12cm,则 此圆锥的侧面积是 .
15.如图,A、B、C三点都在⊙O上,若∠C=34°,则∠AOB的度数是 ;
16.如图1是一种带有黑白双色、边长是20cm的正方形装饰瓷砖,用这样的四块瓷砖可以拼成如图2的图案.已知制作图1这样的瓷砖,其黑、白两部分所用材料的成本分别
三、计算题
四、解答题
17.已知直角中,∠C=90°.
(1)请用直尺和圆规在图中画出直角的外接圆;(不写作法,保留作图痕迹)
(2)若AC=5,BC=12,请求出该直角的外接圆面积.
18.小明用一根铁丝围成了一个面积为25cm2的正方形,小颖对小明说:“我用这根铁丝可以围个面积也是25cm2的圆,且铁丝还有剩余”。问小颖能成功吗?若能,请估计可剩多少厘米的铁丝?(误差小于1cm)若不能,请说明理由。
19.如图,在△ABC中,∠BAC=30°,以AB为直径的⊙O经过点C.过点C作⊙O的切线交AB的延长线于点P.点D为圆上一点,且,弦AD的延长线交切线PC于点E,连接BC.
(1)判断OB和BP的数量关系,并说明理由;
(2)若⊙O的半径为2,求AE的长.
20.如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF,BF,求∠ABF的度数;
(3)如果CD=15,BE=10,sinA=,求⊙O的半径.
21.如图,已知为坐标原点,点的坐标为,的半径为1,过作直线平行于轴,点在上运动.
(1)当点运动到圆上时,求线段的长.
(2)当点的坐标为时,试判断直线与的位置关系,并说明理由.
22.如图,AC是圆O的直径,AC=10厘米,PA,PB是圆O的切线,A,B为切点,过A作AD⊥BP,交BP于D点,连结AB、BC.
(1)求证△ABC∽△ADB;
(2)若切线AP的长为12厘米,求弦AB的长.
23.已知多边形ABDEC是由边长为2的等边三角形ABC和正方形BDEC组成,一圆过A、D、E三点,求该圆半径的长.
24.已知:如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.
求证:(1)△ABC是等边三角形;
(2).
25.已知等边△ABC和⊙M.
(1)如图l,若⊙M与BA的延长线AK及边AC均相切,求证: AM∥BC;
(2)如图2,若⊙M与BA的延长线AK、BC的延长线CF及边AC均相切,求证:四边形ABCM是平行四边形.
参考答案
1.A
2.C。
3. C
4.C
5.D
6.A
7.B
8.A
9.A
10.C
11.
12.12
13.
14.60πcm2。
15.68°
16.6.37
17.(1)略(2)
18.解:设正方形边长为a(cm),周长为c1(cm),圆的半径为R(cm),周长为c2(cm),
由R2=25得R=,∴c2=2R=2()=10=20.又∵,∴17
20.(1)略(2)30°(3)
21.解:(1)如图,设与轴交点为
当点运动到圆上时,有两个位置
,
(2)连接,过作,垂足为
,
在中,
,
直线与相离.
22.(1)证明:∵AC是圆O的直径,∴∠ABC=90 o,
又∵AD⊥BP,∴∠ADB=90 o,∴∠ABC=∠ADB,
又∵PB是圆的切线,∴∠ABD=∠ACB,
在△ABC和△ADB中:
,∴△ABC∽△ADB;
如图,连结OP,
在Rt△AOP中,AP=12厘米,OA=5厘米,根据勾股定理求得OP=13厘米,
又由已知可证得△ABC∽△PAO, ∴,得,解得AB=厘米.
23.2
24.证明:(1)连结OD得OD∥AC ∴∠BDO=∠A 又由OB=OD得∠OBD=∠ODB
∴∠OBD=∠A ∴BC=AC 又∵AB=AC ∴△ABC是等边三角形
(2)连结CD,则CD⊥AB ∴D是AB中点
∵AE=AD=AB ∴EC=3AE ∴.
25.略
