数学中考专题 几何探究——构造辅助圆解决一类动点问题 教学设计
文档属性
| 名称 | 数学中考专题 几何探究——构造辅助圆解决一类动点问题 教学设计 |

|
|
| 格式 | |||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 00:00:00 | ||
图片预览


文档简介
《几何探究——构造辅助圆解决一类动点问题》教学设计
一、教学内容分析
对于平面几何问题,学生常常想到的是构造直线形辅助线来转化条件,从而
利用三角形、四边形的知识来解决问题,但辅助线的添加就被局限在直线形,限
制了学生的思考方向.辅助圆是曲线形辅助线的代表,利用圆,就会让图形的条
件更丰富,而学生对此方法了解较少,于是通过本课对构造辅助圆方法的分类、
典型题的讲解与学生一起探究一类动点问题.由于一节课时间有限,本节课先介
绍辅助圆模型中:“定点+定长”、“直径+直角”、“定弦+定角”、“四点共
圆”模型中的前两种模型.
基于以上分析,本节课的教学重点为:能从具体问题中找出隐含条件,利用
辅助圆解决有关问题.
二、学生学情分析
初三学生掌握了圆的相关性质和应用,但学生对翻折旋转问题、动点问题、
求最值问题有解题困难,图形中的变化性与不变性让学生难以掌握.
基于以上分析,本节课的教学难点为:初步形成用圆的观点看问题的意识,
通过直线型图型在旋转、翻折等变化过程当中的不变性,判断出构造圆的条件,
从而构造出辅助圆.
三、教学目标分析
1.理解通过“圆的两种定义”和“圆周角定理的推论”两种方法构造圆,能掌
握这两种方法的构造条件.
2.能在动点的背景下,通过分析已知条件,找出直线型图形在变化过程当中的
不变性,构造辅助圆模型,渗透模型思想,解决几何问题.
四、教学过程分析
活动一:新课导入,引起兴趣
例 1 如图,在四边形 ABCD中,AB=AC=AD,若∠BAC=25°,∠CAD=75°,
求∠BDC 和∠DBC的度数分别是多少?
设计意图:利用问题激发学习辅助圆模型的需求,引起学生学习兴趣.从而引出
本节课第一个辅助圆模型:定点+定长.
活动二:探索新知,建立模型
模型 1:定点+定长
1.观看微课视频,回顾圆的集合定义和动态定义,学习模型一的方法.
2.建立模型
提问:什么条件让你想到可以构造圆?构造圆的依据是什么?
条件:动点到定点的距离相等.
依据:圆的定义
结论:可构造以定点为圆心,定长为半径的圆.
口诀:找定点(圆心) 寻定长(半径) 现“圆”形
3.运用新知
再次展示例 1的题目,让学生利用“定点+定长”模型构造辅助圆解决这道
题.如图,在四边形 ABCD中,AB=AC=AD,若∠BAC=25°,∠CAD=75°,求
∠BDC和∠DBC的度数分别是多少?
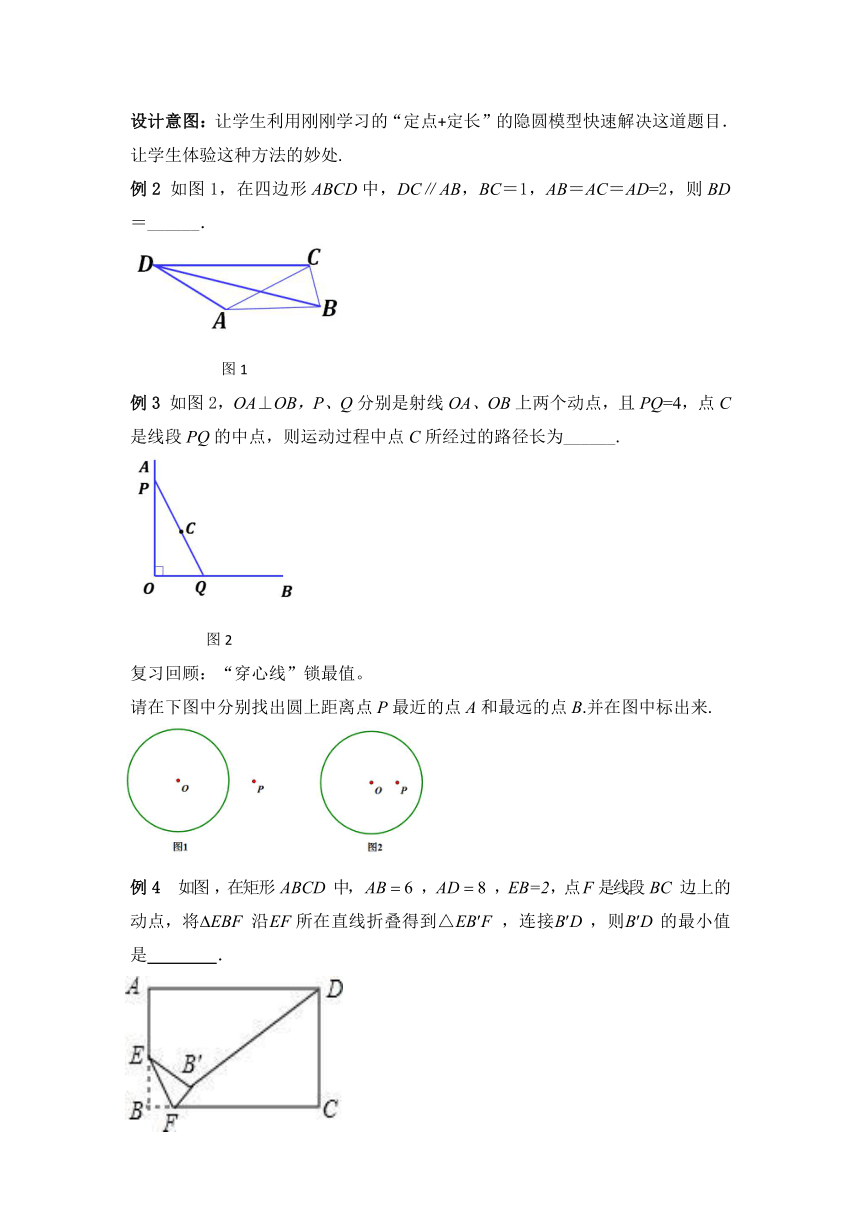
设计意图:让学生利用刚刚学习的“定点+定长”的隐圆模型快速解决这道题目.
让学生体验这种方法的妙处.
例 2 如图 1,在四边形 ABCD中,DC∥AB,BC=1,AB=AC=AD=2,则 BD
=______.
图 1
例 3 如图 2,OA⊥OB,P、Q分别是射线 OA、OB上两个动点,且 PQ=4,点 C
是线段 PQ的中点,则运动过程中点 C所经过的路径长为______.
图 2
复习回顾:“穿心线”锁最值。
请在下图中分别找出圆上距离点 P最近的点 A和最远的点 B.并在图中标出来.
例 4 如图,在矩形 ABCD 中,AB 6 ,AD 8 ,EB=2,点F是线段 BC 边上的
动点,将 EBF 沿EF所在直线折叠得到△EB F ,连接B D ,则B D 的最小值
是 .
5.归纳总结
思考:在什么类型的题目会想到用“定点+定长”模型?
通过 3道例题总结出:当看到直线型图形在旋转、翻折变化过程当中产生一
些不变的线段时,联想到“定点+定长”的方法.
模型二:直径+直角
1.已知线段 AB=8cm,在平面内有一动点 P,满足∠APB=90°.请同学们思考以下
问题:
问题 1:你能找到几个这样的点 P?
师生互动:学生猜想这样的点 P有无数个,老师利用几何画板演示.
问题 2:所有符合条件的点 P组成了什么图形?
学生:发现点 P的运动轨迹构成了圆,且∠APB所对的弦是直径,AB的中点为
圆心.
2.建立模型
提问:什么条件让你想到可以构造圆?构造圆的依据是什么?
条件:若 AB 是固定长度线段,且总有∠ACB=90°.
依据:90°的圆周角所对的弦是直径或直角三角形斜边上的中线等于斜边的一半.
结论:则点 C 在以 AB 为直径的圆上.
口诀:见直角 找直径 定圆心 现“圆”形
例 5(2016 安徽)如图,Rt△ABC 中,AB⊥BC,AB=6,BC=4,P 是△ABC 内
部的一个动点,且满足∠PAB=∠PBC,则线段 CP 长的最小值为( ).
3 8 13 12 13
A. B.2 C. D.
2 13 13
例 6 如图,在正方形 ABCD 中,AB=2,动点 E 从点 A 出发向点 D 运动,同时
动点 F 从点 D 出发向点 C 运动,点 E、F 运动的速度相同,当它们到达各自终
点时停止运动,运动过程中线段 AF、BE 相交于点 P,则线段 DP 的最小值为
_____.
3.归纳总结
思考:在什么类型的题目会想到用“直径+直角”模型?
通过两道例题总结出:当看到题目中有一条固定的线段它所对的角是 90°,
联想到“直径+直角”的方法.
活动三:归纳总结,提炼关键
1.本节课,学习了哪些知识?
2.在“定点+定长”、“直径+直角”两种模型中,无论是利用“圆的定义”
构造圆,还是利用“圆周角定理的推论”构造圆.在动点运动的过程中,有
哪些不变的量?构造辅助圆的关键是什么?
师生活动:学生回答圆心和半径,教师对两个不同方法的条件作归纳,并
总结构造辅助圆的关键是圆心和半径.
3.在今天这节课中,你有什么感受和体会?
不变的量 数形结合
点动、线动、面动 辅助圆 化动为静,解决问题
化归思想
三、课后练习(第 1-4 题为必做题。第 5-7 题为选做题)
1. 如图 3,四边形 ABCD 是矩形,AB=5,AD=4,E 是线段 AD 的中点,F
是线段 AB上一个动点,将△AEF沿 EF所在直线翻折得到△A'EF,连接 A'B,
则线段 A'B 长度的最小值是 .
图 3 图 4 图 5 图 6
2.如图 4,四边形 ABCD 是矩形,AB=5,AD=4,E 是线段 AD 的中点,F是
线段 AB 上一个动点,将△AEF 沿 EF 所在直线翻折得到△A'EF,连接 AA'
与折痕相交于点 P,连接 BP,则线段 BP 长度的最小值是 ..
3.如图 5,△ABC 中,AB=AC=5,BC=2,以 AC 为边在△ABC 外作等边三
角形 ACD,连接 BD,则 BD= .
4.如图 6,在矩形 ABCD 中,已知 AB=2cm,BC=3cm,现有一根长为 2cm 的木棒
EF 紧贴着矩形的边(即两个端点始终落在矩形的边上),按逆时针方向滑动一
周,则木棒 EF 的中点 P 在运动过程中所围成的图形的面积为___________.
5.如图 7,在 Rt△ABC 中,∠C=90°,AC=6,BC=8,点 F 在边 AC 上,并且
CF=2,点 E 为边 BC 上的动点,将△CEF 沿直线 EF 翻折,点 C 落在点 P 处,
则点 P 到边 AB 距离的最小值是___________.
图 7 图 8 图 9
6. 如图 8,⊙O 的半径为 2,弦 AB= 2 3 ,直径 EF⊥AB 于点 H,点 C 在直径
EF 上运动,以弦 AB 为斜边作任意 Rt△ABD,则线段 CD 的最大长度为( ).
A. 2 + 2 B. 2 + 3 C.3+ 3 D.2+ 3
7.如图 9,在矩形 ABCD 中,AB=2,AD=3,点 E、F 分别为 AD、DC 边上的点,
且EF=2,G为 EF的中点,P为BC边上一动点,则PA+PG的最小值为_________.
一、教学内容分析
对于平面几何问题,学生常常想到的是构造直线形辅助线来转化条件,从而
利用三角形、四边形的知识来解决问题,但辅助线的添加就被局限在直线形,限
制了学生的思考方向.辅助圆是曲线形辅助线的代表,利用圆,就会让图形的条
件更丰富,而学生对此方法了解较少,于是通过本课对构造辅助圆方法的分类、
典型题的讲解与学生一起探究一类动点问题.由于一节课时间有限,本节课先介
绍辅助圆模型中:“定点+定长”、“直径+直角”、“定弦+定角”、“四点共
圆”模型中的前两种模型.
基于以上分析,本节课的教学重点为:能从具体问题中找出隐含条件,利用
辅助圆解决有关问题.
二、学生学情分析
初三学生掌握了圆的相关性质和应用,但学生对翻折旋转问题、动点问题、
求最值问题有解题困难,图形中的变化性与不变性让学生难以掌握.
基于以上分析,本节课的教学难点为:初步形成用圆的观点看问题的意识,
通过直线型图型在旋转、翻折等变化过程当中的不变性,判断出构造圆的条件,
从而构造出辅助圆.
三、教学目标分析
1.理解通过“圆的两种定义”和“圆周角定理的推论”两种方法构造圆,能掌
握这两种方法的构造条件.
2.能在动点的背景下,通过分析已知条件,找出直线型图形在变化过程当中的
不变性,构造辅助圆模型,渗透模型思想,解决几何问题.
四、教学过程分析
活动一:新课导入,引起兴趣
例 1 如图,在四边形 ABCD中,AB=AC=AD,若∠BAC=25°,∠CAD=75°,
求∠BDC 和∠DBC的度数分别是多少?
设计意图:利用问题激发学习辅助圆模型的需求,引起学生学习兴趣.从而引出
本节课第一个辅助圆模型:定点+定长.
活动二:探索新知,建立模型
模型 1:定点+定长
1.观看微课视频,回顾圆的集合定义和动态定义,学习模型一的方法.
2.建立模型
提问:什么条件让你想到可以构造圆?构造圆的依据是什么?
条件:动点到定点的距离相等.
依据:圆的定义
结论:可构造以定点为圆心,定长为半径的圆.
口诀:找定点(圆心) 寻定长(半径) 现“圆”形
3.运用新知
再次展示例 1的题目,让学生利用“定点+定长”模型构造辅助圆解决这道
题.如图,在四边形 ABCD中,AB=AC=AD,若∠BAC=25°,∠CAD=75°,求
∠BDC和∠DBC的度数分别是多少?
设计意图:让学生利用刚刚学习的“定点+定长”的隐圆模型快速解决这道题目.
让学生体验这种方法的妙处.
例 2 如图 1,在四边形 ABCD中,DC∥AB,BC=1,AB=AC=AD=2,则 BD
=______.
图 1
例 3 如图 2,OA⊥OB,P、Q分别是射线 OA、OB上两个动点,且 PQ=4,点 C
是线段 PQ的中点,则运动过程中点 C所经过的路径长为______.
图 2
复习回顾:“穿心线”锁最值。
请在下图中分别找出圆上距离点 P最近的点 A和最远的点 B.并在图中标出来.
例 4 如图,在矩形 ABCD 中,AB 6 ,AD 8 ,EB=2,点F是线段 BC 边上的
动点,将 EBF 沿EF所在直线折叠得到△EB F ,连接B D ,则B D 的最小值
是 .
5.归纳总结
思考:在什么类型的题目会想到用“定点+定长”模型?
通过 3道例题总结出:当看到直线型图形在旋转、翻折变化过程当中产生一
些不变的线段时,联想到“定点+定长”的方法.
模型二:直径+直角
1.已知线段 AB=8cm,在平面内有一动点 P,满足∠APB=90°.请同学们思考以下
问题:
问题 1:你能找到几个这样的点 P?
师生互动:学生猜想这样的点 P有无数个,老师利用几何画板演示.
问题 2:所有符合条件的点 P组成了什么图形?
学生:发现点 P的运动轨迹构成了圆,且∠APB所对的弦是直径,AB的中点为
圆心.
2.建立模型
提问:什么条件让你想到可以构造圆?构造圆的依据是什么?
条件:若 AB 是固定长度线段,且总有∠ACB=90°.
依据:90°的圆周角所对的弦是直径或直角三角形斜边上的中线等于斜边的一半.
结论:则点 C 在以 AB 为直径的圆上.
口诀:见直角 找直径 定圆心 现“圆”形
例 5(2016 安徽)如图,Rt△ABC 中,AB⊥BC,AB=6,BC=4,P 是△ABC 内
部的一个动点,且满足∠PAB=∠PBC,则线段 CP 长的最小值为( ).
3 8 13 12 13
A. B.2 C. D.
2 13 13
例 6 如图,在正方形 ABCD 中,AB=2,动点 E 从点 A 出发向点 D 运动,同时
动点 F 从点 D 出发向点 C 运动,点 E、F 运动的速度相同,当它们到达各自终
点时停止运动,运动过程中线段 AF、BE 相交于点 P,则线段 DP 的最小值为
_____.
3.归纳总结
思考:在什么类型的题目会想到用“直径+直角”模型?
通过两道例题总结出:当看到题目中有一条固定的线段它所对的角是 90°,
联想到“直径+直角”的方法.
活动三:归纳总结,提炼关键
1.本节课,学习了哪些知识?
2.在“定点+定长”、“直径+直角”两种模型中,无论是利用“圆的定义”
构造圆,还是利用“圆周角定理的推论”构造圆.在动点运动的过程中,有
哪些不变的量?构造辅助圆的关键是什么?
师生活动:学生回答圆心和半径,教师对两个不同方法的条件作归纳,并
总结构造辅助圆的关键是圆心和半径.
3.在今天这节课中,你有什么感受和体会?
不变的量 数形结合
点动、线动、面动 辅助圆 化动为静,解决问题
化归思想
三、课后练习(第 1-4 题为必做题。第 5-7 题为选做题)
1. 如图 3,四边形 ABCD 是矩形,AB=5,AD=4,E 是线段 AD 的中点,F
是线段 AB上一个动点,将△AEF沿 EF所在直线翻折得到△A'EF,连接 A'B,
则线段 A'B 长度的最小值是 .
图 3 图 4 图 5 图 6
2.如图 4,四边形 ABCD 是矩形,AB=5,AD=4,E 是线段 AD 的中点,F是
线段 AB 上一个动点,将△AEF 沿 EF 所在直线翻折得到△A'EF,连接 AA'
与折痕相交于点 P,连接 BP,则线段 BP 长度的最小值是 ..
3.如图 5,△ABC 中,AB=AC=5,BC=2,以 AC 为边在△ABC 外作等边三
角形 ACD,连接 BD,则 BD= .
4.如图 6,在矩形 ABCD 中,已知 AB=2cm,BC=3cm,现有一根长为 2cm 的木棒
EF 紧贴着矩形的边(即两个端点始终落在矩形的边上),按逆时针方向滑动一
周,则木棒 EF 的中点 P 在运动过程中所围成的图形的面积为___________.
5.如图 7,在 Rt△ABC 中,∠C=90°,AC=6,BC=8,点 F 在边 AC 上,并且
CF=2,点 E 为边 BC 上的动点,将△CEF 沿直线 EF 翻折,点 C 落在点 P 处,
则点 P 到边 AB 距离的最小值是___________.
图 7 图 8 图 9
6. 如图 8,⊙O 的半径为 2,弦 AB= 2 3 ,直径 EF⊥AB 于点 H,点 C 在直径
EF 上运动,以弦 AB 为斜边作任意 Rt△ABD,则线段 CD 的最大长度为( ).
A. 2 + 2 B. 2 + 3 C.3+ 3 D.2+ 3
7.如图 9,在矩形 ABCD 中,AB=2,AD=3,点 E、F 分别为 AD、DC 边上的点,
且EF=2,G为 EF的中点,P为BC边上一动点,则PA+PG的最小值为_________.
同课章节目录
