湘教版数学八年级下册 4.1.2 函数的表示法 教案(表格式)
文档属性
| 名称 | 湘教版数学八年级下册 4.1.2 函数的表示法 教案(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 71.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 00:00:00 | ||
图片预览

文档简介
课题:4.1.2函数的表示法 (教学设计)
教学目标 1.了解并掌握函数表示法:图象法、列表法、公式法。理解并掌握这三种表示法的优缺点; 2.能结合图象对简单实际问题中函数关系进行分析; 3. 能用这三种表示函数的方法解决简单的实际问题.
教学重点:函数的不同表示方法,知道各自的优缺点,能按具体情况选用适当的方法。
教学难点:函数表示方法的应用。
教学过程:
一、知识回顾: 1、说出什么叫做函数? 在一个问题中,存在两个变量, 如果变量y随着变量x而变化, 对于x的每一个确定值, y都有唯一的一个值与它对应, 称y是x的函数. 特别提示: 在考虑两个变量间的函数时,还要注意自变量的取值范围. 2、砸金蛋游戏:砸金蛋,并回答在金蛋的式子中:变量y是不是变量x的函数? (1)y=2x (2) y=x2 (3) y2=x
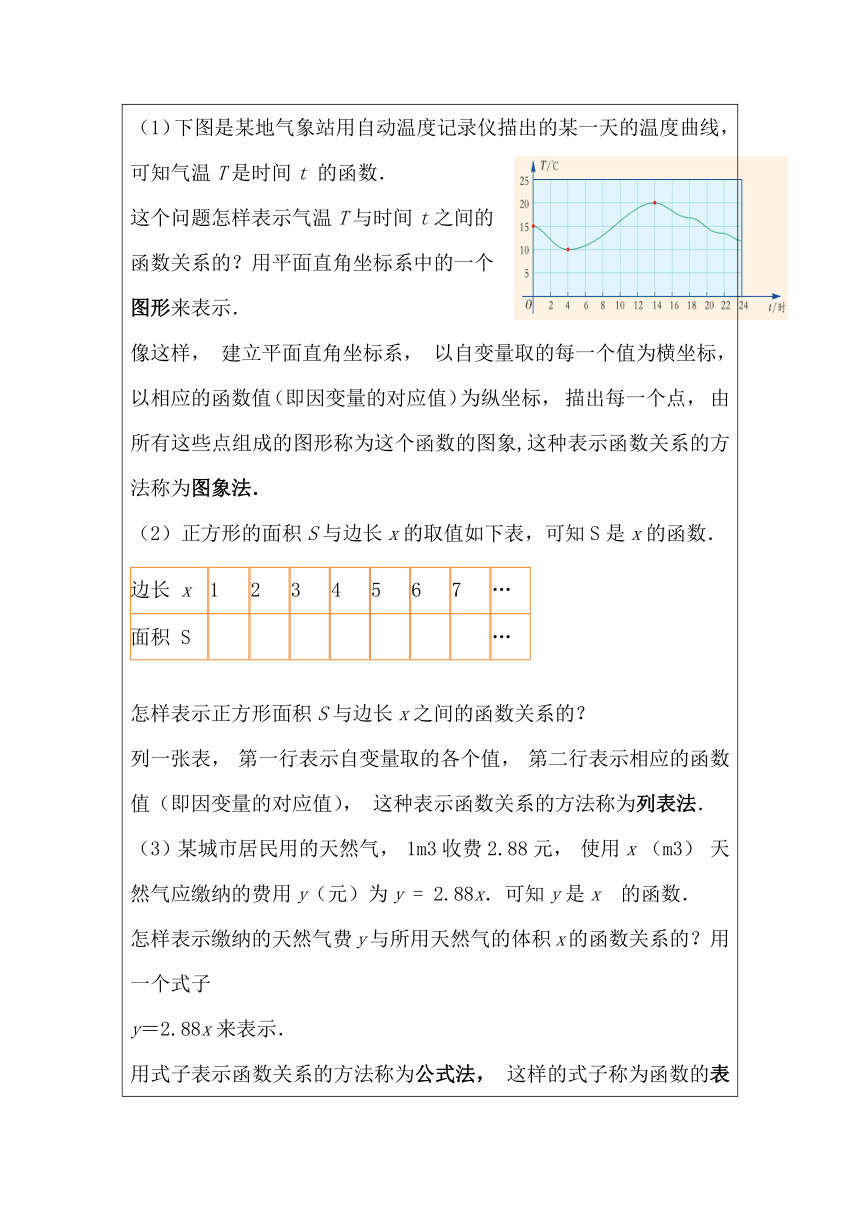
二、探究交流(出示ppt课件) 1、合作探究一:函数的表示方法: (1)下图是某地气象站用自动温度记录仪描出的某一天的温度曲线,可知气温T是时间t 的函数. 这个问题怎样表示气温T与时间t之间的 函数关系的?用平面直角坐标系中的一个 图形来表示. 像这样, 建立平面直角坐标系, 以自变量取的每一个值为横坐标, 以相应的函数值(即因变量的对应值)为纵坐标, 描出每一个点, 由所有这些点组成的图形称为这个函数的图象,这种表示函数关系的方法称为图象法. (2)正方形的面积S与边长x的取值如下表,可知S是x的函数. 边长 x1234567…面积 S …
怎样表示正方形面积S与边长x之间的函数关系的? 列一张表, 第一行表示自变量取的各个值, 第二行表示相应的函数值(即因变量的对应值), 这种表示函数关系的方法称为列表法. (3)某城市居民用的天然气, 1m3收费2.88元, 使用x (m3) 天然气应缴纳的费用y(元)为y = 2.88x.可知y是x 的函数. 怎样表示缴纳的天然气费y与所用天然气的体积x的函数关系的?用一个式子 y=2.88x来表示. 用式子表示函数关系的方法称为公式法, 这样的式子称为函数的表达式(也叫解析式)。 2、合作探究二:函数的三种表示法的优缺点。 用图象法表示函数关系: 优点:可以直观地看出因变量如何随着自变量而变化; 缺点:只能近似求出自变量所对应的函数值,但数量的精确度较差; 用列表法表示函数关系: 优点:可以很清楚地看出自变量取的值与因变量的对应值; 缺点:它只能表示有限个元素间的函数关系,反映的往往是局部的情况。 用公式法表示函数关系: 优点:可以方便地计算函数值. 缺点:不够形象、直观,而且并不是所有函数都能用公式法表示; 3、合作探究三:动脑筋:用三种不同表示方法解决简单的实际问题. 用边长为1的等边三角形拼成如图所示的图形, 用y 表示拼成的图形的周长, 用n表示其中等边三角形的数目, 显然拼成的图形的周长y是n的函数. (1)用列表法表示这个函数关系 (2) 试用公式法表示这个函数关系. (3)试用图象法表示这个函数关系.
三、应用举例 例1. 某天7时,小明从家骑自行车上学, 途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校. 图反映了他骑车的整个过程,结合图象,回答下列问题: (1)自行车发生故障是在什么时间? 此时离家有多远? 解:从横坐标看出, 自行车发生故障的时间是7:05; 从纵坐标看出, 此时离家1000 m. (2) 修车花了多长时间? 修好车后又花了多长时间到达学校? 解:从横坐标看出, 小明修车花了15 min; 小明修好车后又花了10 min到达学校. (3)小明从家到学校的平均速度是多少? 解:从纵坐标看出, 小明家离学校2100 m; 从横坐标看出, 他在路上共花了30 min, 因此, 他从家到学校的平均速度是2 100 ÷ 30 = 70 (m/min).
四、巩固练习(见ppt课件)
五、课堂小结: 1、函数的表示方法有哪些? 2、函数的三种表示方法各自的优点是什么? 3、能用三种表示函数的方法解决简单的实际问题。
六、作业:p116 A 3、4题。
教学目标 1.了解并掌握函数表示法:图象法、列表法、公式法。理解并掌握这三种表示法的优缺点; 2.能结合图象对简单实际问题中函数关系进行分析; 3. 能用这三种表示函数的方法解决简单的实际问题.
教学重点:函数的不同表示方法,知道各自的优缺点,能按具体情况选用适当的方法。
教学难点:函数表示方法的应用。
教学过程:
一、知识回顾: 1、说出什么叫做函数? 在一个问题中,存在两个变量, 如果变量y随着变量x而变化, 对于x的每一个确定值, y都有唯一的一个值与它对应, 称y是x的函数. 特别提示: 在考虑两个变量间的函数时,还要注意自变量的取值范围. 2、砸金蛋游戏:砸金蛋,并回答在金蛋的式子中:变量y是不是变量x的函数? (1)y=2x (2) y=x2 (3) y2=x
二、探究交流(出示ppt课件) 1、合作探究一:函数的表示方法: (1)下图是某地气象站用自动温度记录仪描出的某一天的温度曲线,可知气温T是时间t 的函数. 这个问题怎样表示气温T与时间t之间的 函数关系的?用平面直角坐标系中的一个 图形来表示. 像这样, 建立平面直角坐标系, 以自变量取的每一个值为横坐标, 以相应的函数值(即因变量的对应值)为纵坐标, 描出每一个点, 由所有这些点组成的图形称为这个函数的图象,这种表示函数关系的方法称为图象法. (2)正方形的面积S与边长x的取值如下表,可知S是x的函数. 边长 x1234567…面积 S …
怎样表示正方形面积S与边长x之间的函数关系的? 列一张表, 第一行表示自变量取的各个值, 第二行表示相应的函数值(即因变量的对应值), 这种表示函数关系的方法称为列表法. (3)某城市居民用的天然气, 1m3收费2.88元, 使用x (m3) 天然气应缴纳的费用y(元)为y = 2.88x.可知y是x 的函数. 怎样表示缴纳的天然气费y与所用天然气的体积x的函数关系的?用一个式子 y=2.88x来表示. 用式子表示函数关系的方法称为公式法, 这样的式子称为函数的表达式(也叫解析式)。 2、合作探究二:函数的三种表示法的优缺点。 用图象法表示函数关系: 优点:可以直观地看出因变量如何随着自变量而变化; 缺点:只能近似求出自变量所对应的函数值,但数量的精确度较差; 用列表法表示函数关系: 优点:可以很清楚地看出自变量取的值与因变量的对应值; 缺点:它只能表示有限个元素间的函数关系,反映的往往是局部的情况。 用公式法表示函数关系: 优点:可以方便地计算函数值. 缺点:不够形象、直观,而且并不是所有函数都能用公式法表示; 3、合作探究三:动脑筋:用三种不同表示方法解决简单的实际问题. 用边长为1的等边三角形拼成如图所示的图形, 用y 表示拼成的图形的周长, 用n表示其中等边三角形的数目, 显然拼成的图形的周长y是n的函数. (1)用列表法表示这个函数关系 (2) 试用公式法表示这个函数关系. (3)试用图象法表示这个函数关系.
三、应用举例 例1. 某天7时,小明从家骑自行车上学, 途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校. 图反映了他骑车的整个过程,结合图象,回答下列问题: (1)自行车发生故障是在什么时间? 此时离家有多远? 解:从横坐标看出, 自行车发生故障的时间是7:05; 从纵坐标看出, 此时离家1000 m. (2) 修车花了多长时间? 修好车后又花了多长时间到达学校? 解:从横坐标看出, 小明修车花了15 min; 小明修好车后又花了10 min到达学校. (3)小明从家到学校的平均速度是多少? 解:从纵坐标看出, 小明家离学校2100 m; 从横坐标看出, 他在路上共花了30 min, 因此, 他从家到学校的平均速度是2 100 ÷ 30 = 70 (m/min).
四、巩固练习(见ppt课件)
五、课堂小结: 1、函数的表示方法有哪些? 2、函数的三种表示方法各自的优点是什么? 3、能用三种表示函数的方法解决简单的实际问题。
六、作业:p116 A 3、4题。
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
