华东师大版九年级数学上册 第22章 达标检测卷(word版含答案)
文档属性
| 名称 | 华东师大版九年级数学上册 第22章 达标检测卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 185.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 14:05:57 | ||
图片预览




文档简介
华东师大版九年级数学上册 第22章 达标检测卷
(限时: 120分钟 满分: 150分)
班级: 姓名: 得分:
一、选择题(本题共10小题,每小题5分,共50分)
1.已知(m-2)xm2-2-x+3=0是关于x的一元二次方程,则m的值是( )
A.m=±2 B.m=2
C.m=-2 D.以上都不对
2.一元二次方程x2+2x=0的解为( )
A.x=-2 B.x=2
C.x1=0,x2=-2 D.x1=0,x2=2
3.已知一元二次方程x2+4x-3=0,下列配方正确的是( )
A.(x+2)2=3 B.(x-2)2=3
C.(x+2)2=7 D.(x-2)2=7
4.下列方程中有两个相等实数根的是( )
A.(x-1)(x+1)=0 B.(x-1)(x-1)=0
C.(x-1)2=4 D.x(x-1)=0
5.对于一元二次方程2x2-3x+4=0,它的根的情况为( )
A.没有实数根 B.两根之和是3
C.两根之积是-2 D.有两个不相等的实数根
6.用换元法解方程+=2时,若设=y,则原方程可化为关于y的方程( )
A.y2-2y+1=0 B.y2+2y+1=0
C.y2+y+2=0 D.y2+y-2=0
7.已知a、b是关于x的一元二次方程x2-6x-n+1=0的两个根,若a、b、5为等腰三角形的边长,则n的值为( )
A.-4 B.8
C.-4或-8 D.4或-8
8.为响应“坚持绿色低碳,建设一个清洁美丽的世界”的号召,某市今年第一季度进行宣传准备工作,从第二季度开始到今年年底全市全面实现垃圾分类.已知该市一共有285个社区,第二季度已有60个社区实现垃圾分类,第三、四季度实现垃圾分类的社区个数较前一季度平均增长率均为x,则下面所列方程正确的是( )
A.60(1+x)2=285
B.60(1-x)2=285
C.60(1+x)+60(1+x)2=285
D.60+60(1+x)+60(1+x)2=285
9.已知m、n是一元二次方程x2+x-2 022=0的两个实数根,则代数式m2+2m+n的值等于( )
A.2 019 B.2 020 C.2 021 D.2 022
10.定义新运算“※”:对于实数m、n、p、q,有[m,p]※[q,n]=mn+pq,其中等式右边是通常的加法和乘法运算,例如:[2,3]※[4,5]=2×5+3×4=22.若关于x的方程[x2+1,x]※[5-2k,k]=0有两个实数根,则k的取值范围是 ( )
A.k<2且k≠0 B.k≤
C.k≤且k≠0 D.k≥
二、填空题(本题共6小题,每小题5分,共30分)
11.方程2x(x-4)=0的解为________________.
12.若关于x的方程x2-kx-12=0的一个根为3,则k的值为________.
13.若将方程x2-6x=7化成(x+m)2=b,则m+b=____________________________________.
14.如图,学校准备修建一个面积为48 m2的矩形花园.它的一边靠墙,其余三边利用长20 m的围栏,已知墙长9 m,则围成矩形的长为________m.
INCLUDEPICTURE"SLH22-7.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\9HS福建\\SLH22-7.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\22秋点训数学HS福建9年级\\word\\SLH22-7.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\22秋点训数学HS福建9年级\\word\\SLH22-7.tif" \* MERGEFORMATINET
(第14题)
15.教师节当天,某校数学老师向本组其他老师各发一条祝福短信,据统计,全组共发了240条祝福短信,则全组有老师________人.
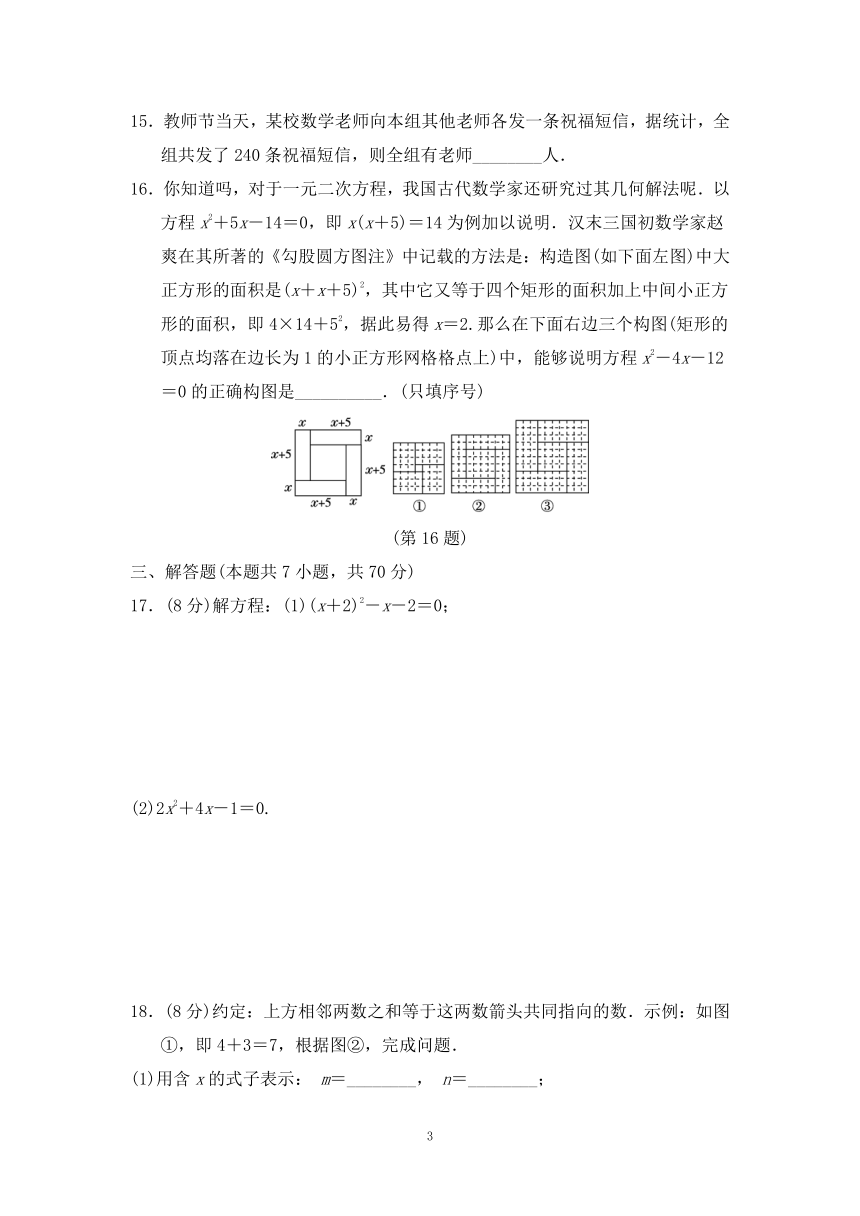
16.你知道吗,对于一元二次方程,我国古代数学家还研究过其几何解法呢.以方程x2+5x-14=0,即x(x+5)=14为例加以说明.汉末三国初数学家赵爽在其所著的《勾股圆方图注》中记载的方法是:构造图(如下面左图)中大正方形的面积是(x+x+5)2,其中它又等于四个矩形的面积加上中间小正方形的面积,即4×14+52,据此易得x=2.那么在下面右边三个构图(矩形的顶点均落在边长为1的小正方形网格格点上)中,能够说明方程x2-4x-12=0的正确构图是__________.(只填序号)
INCLUDEPICTURE"加208.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\9HS福建\\加208.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\22秋点训数学HS福建9年级\\word\\加208.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\22秋点训数学HS福建9年级\\word\\加208.tif" \* MERGEFORMATINET
(第16题)
三、解答题(本题共7小题,共70分)
17.(8分)解方程:(1)(x+2)2-x-2=0;
(2)2x2+4x-1=0.
18.(8分)约定:上方相邻两数之和等于这两数箭头共同指向的数.示例:如图①,即4+3=7,根据图②,完成问题.
(1)用含x的式子表示: m=________, n=________;
(2)当y=3时,求x的值.
INCLUDEPICTURE"2022SXJ22-1.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\9HS福建\\2022SXJ22-1.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\22秋点训数学HS福建9年级\\word\\2022SXJ22-1.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\22秋点训数学HS福建9年级\\word\\2022SXJ22-1.tif" \* MERGEFORMATINET
(第18题)
19.(10分)已知关于x的方程b(x2-1)+2ax+c(x2+1)=0,其中a、b、c分别为△ABC三边的长.
(1)若x=-1是方程的根,试判断△ABC的形状;
(2)若△ABC是等边三角形,试求这个方程的根;
(3)若方程有两个相等的实数根,且a=5,b=12,求c的值.
20.(10分)为培养学生的阅读兴趣,学校开展了课外阅读活动,计划将学生人均阅读量从七年级第一学期的 70万字增加到八年级第一学期的100.8万字.
(1)如果每学期学生人均阅读量的平均增长率相同,求这个增长率;
(2)按照(1)中的阅读量增长率,学校期望八年级第二学期的人均阅读量达到120万,请通过计算说明他们的目标能否实现.
21.(10分)已知关于x的一元二次方程x2-(m+2)x+3(m-1)=0.
(1)请判断这个方程的根的情况,并说明理由;
(2)若这个方程的一个实数根大于1,另一个实数根小于0 ,求m的取值范围.
22.(12分)如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点Q从点A开始沿AB边向点B以1 cm/s的速度移动,点P从点B开始沿BC边向点C以2 cm/s的速度移动.
(1)如果P、Q两点同时出发,那么几秒后,△PBQ的面积等于4 cm2
(2)△PBQ的面积能否等于7cm2?试说明理由.
INCLUDEPICTURE"B-9.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\9HS福建\\B-9.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\22秋点训数学HS福建9年级\\word\\B-9.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\22秋点训数学HS福建9年级\\word\\B-9.tif" \* MERGEFORMATINET
(第22题)
23.(12分)阅读下面材料,并完成问题.
任意给定一个矩形A,若存在另一个矩形B,使它的周长和面积分别是矩形A的一半,则称矩形A、B是“兄弟矩形”.
探究:当矩形A的长、宽分别为7和1时,是否存在A的“兄弟矩形”B
小亮同学是这样探究的:
设所求矩形的相邻两边长分别是x和y,由题意
得
由①得y=4-x,③
把③代入②,得x(4-x)=,
整理得2x2-8x+7=0.
∵b2-4ac=64-56=8>0,
∴A的“兄弟矩形”B存在.
(1)若已知矩形A的长、宽分别为3和2,请你根据小亮的探究方法,说明A的“兄弟矩形”B是否存在;
(2)若矩形A的相邻两边长为m和n,当A的“兄弟矩形”B存在时,求m、n应满足的条件.
答案
一、1.C 2.C 3.C 4.B 5.A 6.A 7.C 8.D 9.C 10.C
二、11.x1=0,x2=4
12.-1 13.13 14.8
15.16 16.②
三、17.解:(1)(x+2)2-(x+2)=0,
(x+2)(x+2-1)=0,
(x+2)(x+1)=0,
∴x+2=0或x+1=0,
∴x1=-2,x2=-1.
(2)∵a=2,b=4,c=-1,
∴b2-4ac=24,
∴x==,
∴x1=,x2=.
18.解:(1)2x2+x;2x2+3
(2)∵m=2x2+x,n=2x2+3,
∴y=m+n=2x2+x+2x2+3=4x2+x+3.
又∵y=3, ∴3=4x2+x+3,
整理得4x2+x=0,
解得x1=0,x2=-.
∴当y=3时, x的值为0或-.
19.解:(1)将x=-1代入方程,得-2a+2c=0,解得a=c,
∴△ABC为等腰三角形.
(2)∵△ABC是等边三角形,∴a=b=c≠0,
∴(x2-1)+2x+(x2+1)=0,
化简得x2+x=0,解得x1=0,x2=-1.
(3)将a=5,b=12代入方程得
12(x2-1)+10x+c(x2+1)=0,
化简得(12+c)x2+10x+c-12=0,
∵方程有两个相等的实数根,
∴Δ=102-4(12+c)(c-12)=0,
化简得c2=169,
解得c=13或c=-13(舍去),
c=13符合三角形三边关系,
∴ c=13.
20.解:(1)设每学期学生人均阅读量的平均增长率为x,
依题意得70(1+x)2=100.8,
解得x1=0.2=20%,x2=-2.2(不合题意,舍去).
答:每学期学生人均阅读量的平均增长率为20%.
(2)100.8×(1+20%)=120.96(万字).
∵120.96万字>120万字,
答:他们的目标能实现.
21.解:(1)依题意得
Δ=[-(m+2)]2-4×3(m-1)=m2-8m+16=(m-4)2≥0.
∴方程x2-(m+2)x+3(m-1)=0有两个实数根.
(2)依题意得
x==.
∴x1=m-1,x2=3.
∵方程的一个实数根大于1,另一个实数根小于0,
∴x=m-1<0.
∴m<1.
22.解:(1)设t s后,△PBQ的面积等于4cm2,
则(5-t)×2t=4,
整理得
t2-5t+4=0,
解得t1=1,t2=4(舍去).
∴如果P、Q两点同时出发,那么1 s后,△PBQ的面积等于4 cm2.
(2)△PBQ的面积不能等于7 cm2.理由如下:
设x s后,△PBQ的面积等于7 cm2,则
(5-x)×2x=7,
整理得
x2-5x+7=0,
则Δ=25-28=-3<0,
所以该方程无实数根.
故△PBQ的面积不能等于7cm2.
23.解:(1)设所求矩形的相邻两边长分别是x和y,由题意得
由①得y=-x,③
把③代入②,得x=3.
整理得2x2 -5x+6=0,
∵b2-4ac=25-48=-23<0,
∴A的“兄弟矩形”B不存在.
(2)设所求矩形的相邻两边长分别是x和y,
由题意得
由①得y=-x,③
把③代入②,得x=.
整理得2x2-(m+n)x+mn=0,
∵b2-4ac=[-(m+n)]2-8mn=m2-6mn+n2,
且x、y都是正数,
∴当m2- 6mn+n2≥0时,A的“兄弟矩形”B存在.
PAGE
(限时: 120分钟 满分: 150分)
班级: 姓名: 得分:
一、选择题(本题共10小题,每小题5分,共50分)
1.已知(m-2)xm2-2-x+3=0是关于x的一元二次方程,则m的值是( )
A.m=±2 B.m=2
C.m=-2 D.以上都不对
2.一元二次方程x2+2x=0的解为( )
A.x=-2 B.x=2
C.x1=0,x2=-2 D.x1=0,x2=2
3.已知一元二次方程x2+4x-3=0,下列配方正确的是( )
A.(x+2)2=3 B.(x-2)2=3
C.(x+2)2=7 D.(x-2)2=7
4.下列方程中有两个相等实数根的是( )
A.(x-1)(x+1)=0 B.(x-1)(x-1)=0
C.(x-1)2=4 D.x(x-1)=0
5.对于一元二次方程2x2-3x+4=0,它的根的情况为( )
A.没有实数根 B.两根之和是3
C.两根之积是-2 D.有两个不相等的实数根
6.用换元法解方程+=2时,若设=y,则原方程可化为关于y的方程( )
A.y2-2y+1=0 B.y2+2y+1=0
C.y2+y+2=0 D.y2+y-2=0
7.已知a、b是关于x的一元二次方程x2-6x-n+1=0的两个根,若a、b、5为等腰三角形的边长,则n的值为( )
A.-4 B.8
C.-4或-8 D.4或-8
8.为响应“坚持绿色低碳,建设一个清洁美丽的世界”的号召,某市今年第一季度进行宣传准备工作,从第二季度开始到今年年底全市全面实现垃圾分类.已知该市一共有285个社区,第二季度已有60个社区实现垃圾分类,第三、四季度实现垃圾分类的社区个数较前一季度平均增长率均为x,则下面所列方程正确的是( )
A.60(1+x)2=285
B.60(1-x)2=285
C.60(1+x)+60(1+x)2=285
D.60+60(1+x)+60(1+x)2=285
9.已知m、n是一元二次方程x2+x-2 022=0的两个实数根,则代数式m2+2m+n的值等于( )
A.2 019 B.2 020 C.2 021 D.2 022
10.定义新运算“※”:对于实数m、n、p、q,有[m,p]※[q,n]=mn+pq,其中等式右边是通常的加法和乘法运算,例如:[2,3]※[4,5]=2×5+3×4=22.若关于x的方程[x2+1,x]※[5-2k,k]=0有两个实数根,则k的取值范围是 ( )
A.k<2且k≠0 B.k≤
C.k≤且k≠0 D.k≥
二、填空题(本题共6小题,每小题5分,共30分)
11.方程2x(x-4)=0的解为________________.
12.若关于x的方程x2-kx-12=0的一个根为3,则k的值为________.
13.若将方程x2-6x=7化成(x+m)2=b,则m+b=____________________________________.
14.如图,学校准备修建一个面积为48 m2的矩形花园.它的一边靠墙,其余三边利用长20 m的围栏,已知墙长9 m,则围成矩形的长为________m.
INCLUDEPICTURE"SLH22-7.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\9HS福建\\SLH22-7.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\22秋点训数学HS福建9年级\\word\\SLH22-7.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\22秋点训数学HS福建9年级\\word\\SLH22-7.tif" \* MERGEFORMATINET
(第14题)
15.教师节当天,某校数学老师向本组其他老师各发一条祝福短信,据统计,全组共发了240条祝福短信,则全组有老师________人.
16.你知道吗,对于一元二次方程,我国古代数学家还研究过其几何解法呢.以方程x2+5x-14=0,即x(x+5)=14为例加以说明.汉末三国初数学家赵爽在其所著的《勾股圆方图注》中记载的方法是:构造图(如下面左图)中大正方形的面积是(x+x+5)2,其中它又等于四个矩形的面积加上中间小正方形的面积,即4×14+52,据此易得x=2.那么在下面右边三个构图(矩形的顶点均落在边长为1的小正方形网格格点上)中,能够说明方程x2-4x-12=0的正确构图是__________.(只填序号)
INCLUDEPICTURE"加208.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\9HS福建\\加208.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\22秋点训数学HS福建9年级\\word\\加208.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\22秋点训数学HS福建9年级\\word\\加208.tif" \* MERGEFORMATINET
(第16题)
三、解答题(本题共7小题,共70分)
17.(8分)解方程:(1)(x+2)2-x-2=0;
(2)2x2+4x-1=0.
18.(8分)约定:上方相邻两数之和等于这两数箭头共同指向的数.示例:如图①,即4+3=7,根据图②,完成问题.
(1)用含x的式子表示: m=________, n=________;
(2)当y=3时,求x的值.
INCLUDEPICTURE"2022SXJ22-1.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\9HS福建\\2022SXJ22-1.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\22秋点训数学HS福建9年级\\word\\2022SXJ22-1.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\22秋点训数学HS福建9年级\\word\\2022SXJ22-1.tif" \* MERGEFORMATINET
(第18题)
19.(10分)已知关于x的方程b(x2-1)+2ax+c(x2+1)=0,其中a、b、c分别为△ABC三边的长.
(1)若x=-1是方程的根,试判断△ABC的形状;
(2)若△ABC是等边三角形,试求这个方程的根;
(3)若方程有两个相等的实数根,且a=5,b=12,求c的值.
20.(10分)为培养学生的阅读兴趣,学校开展了课外阅读活动,计划将学生人均阅读量从七年级第一学期的 70万字增加到八年级第一学期的100.8万字.
(1)如果每学期学生人均阅读量的平均增长率相同,求这个增长率;
(2)按照(1)中的阅读量增长率,学校期望八年级第二学期的人均阅读量达到120万,请通过计算说明他们的目标能否实现.
21.(10分)已知关于x的一元二次方程x2-(m+2)x+3(m-1)=0.
(1)请判断这个方程的根的情况,并说明理由;
(2)若这个方程的一个实数根大于1,另一个实数根小于0 ,求m的取值范围.
22.(12分)如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点Q从点A开始沿AB边向点B以1 cm/s的速度移动,点P从点B开始沿BC边向点C以2 cm/s的速度移动.
(1)如果P、Q两点同时出发,那么几秒后,△PBQ的面积等于4 cm2
(2)△PBQ的面积能否等于7cm2?试说明理由.
INCLUDEPICTURE"B-9.tif" INCLUDEPICTURE "C:\\Users\\Administrator\\Desktop\\9HS福建\\B-9.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\22秋点训数学HS福建9年级\\word\\B-9.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\22秋点训数学HS福建9年级\\word\\B-9.tif" \* MERGEFORMATINET
(第22题)
23.(12分)阅读下面材料,并完成问题.
任意给定一个矩形A,若存在另一个矩形B,使它的周长和面积分别是矩形A的一半,则称矩形A、B是“兄弟矩形”.
探究:当矩形A的长、宽分别为7和1时,是否存在A的“兄弟矩形”B
小亮同学是这样探究的:
设所求矩形的相邻两边长分别是x和y,由题意
得
由①得y=4-x,③
把③代入②,得x(4-x)=,
整理得2x2-8x+7=0.
∵b2-4ac=64-56=8>0,
∴A的“兄弟矩形”B存在.
(1)若已知矩形A的长、宽分别为3和2,请你根据小亮的探究方法,说明A的“兄弟矩形”B是否存在;
(2)若矩形A的相邻两边长为m和n,当A的“兄弟矩形”B存在时,求m、n应满足的条件.
答案
一、1.C 2.C 3.C 4.B 5.A 6.A 7.C 8.D 9.C 10.C
二、11.x1=0,x2=4
12.-1 13.13 14.8
15.16 16.②
三、17.解:(1)(x+2)2-(x+2)=0,
(x+2)(x+2-1)=0,
(x+2)(x+1)=0,
∴x+2=0或x+1=0,
∴x1=-2,x2=-1.
(2)∵a=2,b=4,c=-1,
∴b2-4ac=24,
∴x==,
∴x1=,x2=.
18.解:(1)2x2+x;2x2+3
(2)∵m=2x2+x,n=2x2+3,
∴y=m+n=2x2+x+2x2+3=4x2+x+3.
又∵y=3, ∴3=4x2+x+3,
整理得4x2+x=0,
解得x1=0,x2=-.
∴当y=3时, x的值为0或-.
19.解:(1)将x=-1代入方程,得-2a+2c=0,解得a=c,
∴△ABC为等腰三角形.
(2)∵△ABC是等边三角形,∴a=b=c≠0,
∴(x2-1)+2x+(x2+1)=0,
化简得x2+x=0,解得x1=0,x2=-1.
(3)将a=5,b=12代入方程得
12(x2-1)+10x+c(x2+1)=0,
化简得(12+c)x2+10x+c-12=0,
∵方程有两个相等的实数根,
∴Δ=102-4(12+c)(c-12)=0,
化简得c2=169,
解得c=13或c=-13(舍去),
c=13符合三角形三边关系,
∴ c=13.
20.解:(1)设每学期学生人均阅读量的平均增长率为x,
依题意得70(1+x)2=100.8,
解得x1=0.2=20%,x2=-2.2(不合题意,舍去).
答:每学期学生人均阅读量的平均增长率为20%.
(2)100.8×(1+20%)=120.96(万字).
∵120.96万字>120万字,
答:他们的目标能实现.
21.解:(1)依题意得
Δ=[-(m+2)]2-4×3(m-1)=m2-8m+16=(m-4)2≥0.
∴方程x2-(m+2)x+3(m-1)=0有两个实数根.
(2)依题意得
x==.
∴x1=m-1,x2=3.
∵方程的一个实数根大于1,另一个实数根小于0,
∴x=m-1<0.
∴m<1.
22.解:(1)设t s后,△PBQ的面积等于4cm2,
则(5-t)×2t=4,
整理得
t2-5t+4=0,
解得t1=1,t2=4(舍去).
∴如果P、Q两点同时出发,那么1 s后,△PBQ的面积等于4 cm2.
(2)△PBQ的面积不能等于7 cm2.理由如下:
设x s后,△PBQ的面积等于7 cm2,则
(5-x)×2x=7,
整理得
x2-5x+7=0,
则Δ=25-28=-3<0,
所以该方程无实数根.
故△PBQ的面积不能等于7cm2.
23.解:(1)设所求矩形的相邻两边长分别是x和y,由题意得
由①得y=-x,③
把③代入②,得x=3.
整理得2x2 -5x+6=0,
∵b2-4ac=25-48=-23<0,
∴A的“兄弟矩形”B不存在.
(2)设所求矩形的相邻两边长分别是x和y,
由题意得
由①得y=-x,③
把③代入②,得x=.
整理得2x2-(m+n)x+mn=0,
∵b2-4ac=[-(m+n)]2-8mn=m2-6mn+n2,
且x、y都是正数,
∴当m2- 6mn+n2≥0时,A的“兄弟矩形”B存在.
PAGE
