湘教版九年级数学上册 第3章 图形的相似 达标检测卷(word版含答案)
文档属性
| 名称 | 湘教版九年级数学上册 第3章 图形的相似 达标检测卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 226.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 14:10:48 | ||
图片预览



文档简介
湘教版九年级数学上册 第3章 达标检测卷
(限时: 120分钟 满分: 100分)
班级: 姓名: 得分:
一、选择题(每题3分,共18分)
1.下列四组线段中,是成比例线段的是( )
A.3,6,9,16 B.2,3,4,5
C.,,,5 D.5,2,3,6
2.如图,∠B=∠ACD,则哪条线段与AD的比等于△ABC与△ACD周长之比? ( )
A.BC B.AC
C.AB D.BD
INCLUDEPICTURE"J3-1.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J3-1.tif" \* MERGEFORMATINET INCLUDEPICTURE"J3-2.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J3-2.tif" \* MERGEFORMATINET INCLUDEPICTURE"J3-3.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J3-3.tif" \* MERGEFORMATINET INCLUDEPICTURE"J3-5.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J3-5.tif" \* MERGEFORMATINET
(第2题) (第3题) (第4题) (第6题)
3.如图,在△ABC中,点D,E分别在AB,AC边上,AD=2,AB=6,添加下列条件不—定能判定DE∥BC的是( )
A.= B.=
C.= D.=
4.如图,在平面直角坐标系中,△ABC与△DEF是以坐标原点O为位似中心的位似图形,若A(-2,0),D(3,0),且BC=3,则线段EF的长度为( )
A.2 B.4
C. D.6
5.已知点P是线段AB的黄金分割点,AP>PB,则AP∶PB的值为( )
A. B.-1
C.0.618 D.
6.如图,已知△ABC和△EDF的顶点都在正方形网格的格点上,则∠ABC+∠ACB的度数为( )
A.30° B.45°
C.60° D.75°
二、填空题(每题4分,共24分)
7.已知=,则=________.
8.如图,△ABC中,BC>BA,点D是BC边上的一个动点(点D与点B,C不重合),若再增加一个条件,就能使△ABD与△ABC相似,则这个条件可以是________(写出一个即可).
INCLUDEPICTURE"J3-6.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J3-6.tif" \* MERGEFORMATINET INCLUDEPICTURE"J3-7.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J3-7.tif" \* MERGEFORMATINET
(第8题) (第10题)
9.若△ABC∽△A′B′C′,且△ABC与△A′B′C′的面积之比为3∶4,则∠ABC与∠A′B′C′的平分线之比为________.
10.如图,已知AB∥CD∥EF,=,BE=15,那么CE的长为________.
11.如图,在△ABC与△DEF中,=,∠B=∠E, CM⊥AB,FN⊥DE,G、H分别是BC、EF的中点.若=,则=____________.
INCLUDEPICTURE"SXJ3-7.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\SXJ3-7.tif" \* MERGEFORMATINET INCLUDEPICTURE"J3-8.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J3-8.tif" \* MERGEFORMATINET
(第11题) (第12题)
12.如图,△ABC的顶点B在反比例函数y=(x>0)的图象上,顶点C在x轴负半轴上,AB∥x轴,AB,BC分别交y轴于点D,E.若==,S△ABC=13,则k=________.
三、解答题(13,14题每题8分,18题12分,其余每题10分,共58分)
13.已知==,2x+y+z=45,求代数式3x+2y-z的值.
14.如图,△ACC′是由△ABB′经过位似变换得到的.
(1)△ACC′与△ABB′的相似比为________,它们的位似中心是点________.
(2)△AEE′是△ABB′的位似图形吗?如果是,求相似比;如果不是,说明理由.
(3)图中是否存在一个三角形与△ABB′位似,且位似比为3∶1?如果存在,请写出符合条件的三角形;若不存在,说明理由.
INCLUDEPICTURE"J3-9.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J3-9.tif" \* MERGEFORMATINET
(第14题)
15.如图,D是△ABC的边AB的中点,DE∥BC,CE∥AB,AC与DE相交于点F.
求证:F是DE的中点.
INCLUDEPICTURE"J3-10.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J3-10.tif" \* MERGEFORMATINET
(第15题)
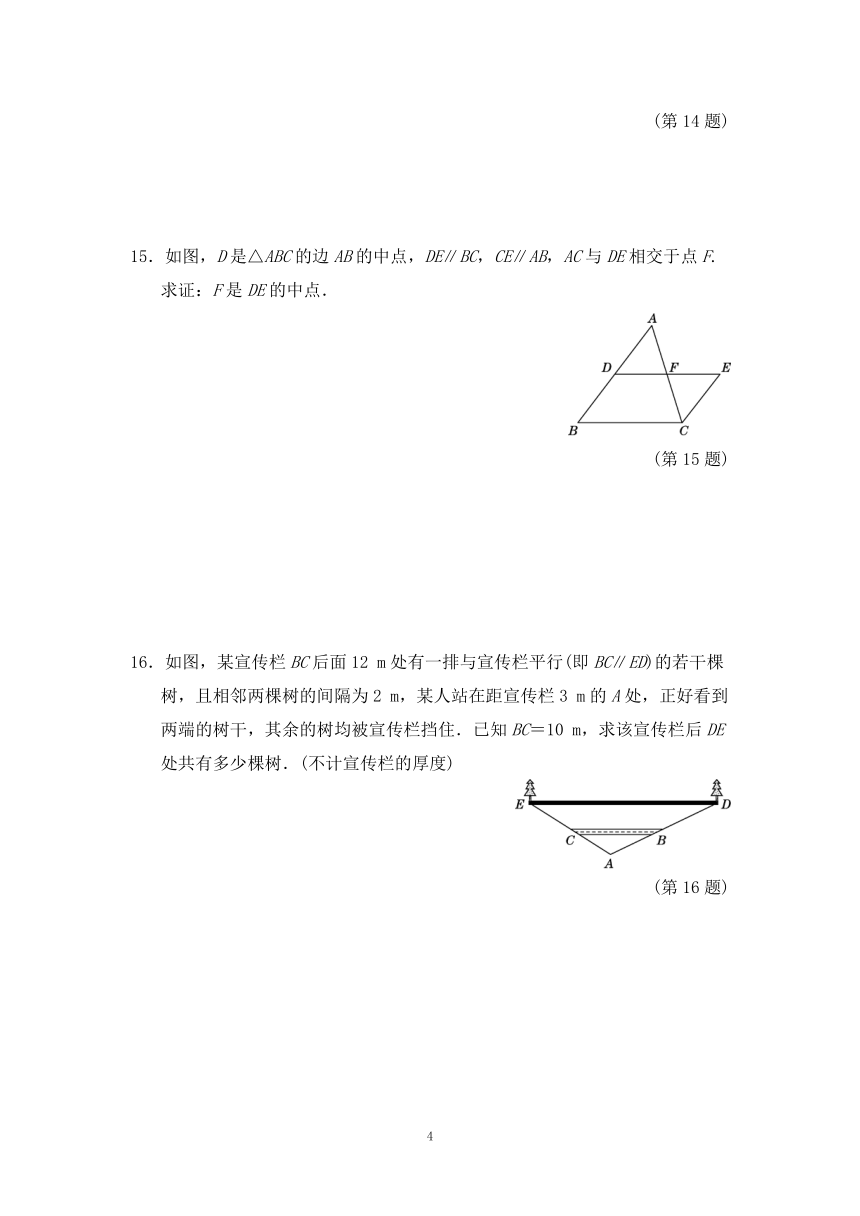
16.如图,某宣传栏BC后面12 m处有一排与宣传栏平行(即BC∥ED)的若干棵树,且相邻两棵树的间隔为2 m,某人站在距宣传栏3 m的A处,正好看到两端的树干,其余的树均被宣传栏挡住.已知BC=10 m,求该宣传栏后DE处共有多少棵树.(不计宣传栏的厚度)
INCLUDEPICTURE"J3-11.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J3-11.tif" \* MERGEFORMATINET
(第16题)
17.如图,在△ABC中,AD平分∠BAC,与BC相交于点D,点E,F分别在线段AB,AD上,且∠EFD=∠BDF.
(1)求证:△AFE∽△ADC.
(2)若=,AE=2EB,且∠AFE=∠C,试探究线段DF与BE之间的数量关系.
INCLUDEPICTURE"J3-12.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J3-12.tif" \* MERGEFORMATINET
(第17题)
18.如图,矩形ABCD中,AB=3cm,BC=6cm.某一时刻,动点M从点A出发沿AB方向以1cm/s的速度向点B匀速运动,同时动点N从点D出发沿DA方向以2cm/s的速度向点A匀速运动,设运动时间为t s.问是否存在t,使以A、M、N为顶点的三角形与△ACD相似?若存在,求出t的值;若不存在,请说明理由.
INCLUDEPICTURE"J3-13.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J3-13.tif" \* MERGEFORMATINET
(第18题)
答案
一、1.C 2.B 3.A 4.C 5.D 6.B
二、7.
8.(答案不唯一)∠BAD=∠C
9.
10.6 点拨:∵AB∥CD∥EF,∴=,即=,解得CE=6.
11.
12.18 点拨:如图,过点B作BF⊥x轴于点F.
∵AB∥x轴,∴△DBE∽△OCE,
INCLUDEPICTURE"DJ3-1.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\DJ3-1.tif" \* MERGEFORMATINET
(第12题)
∴==.
∵==,∴====,
设CO=3a,DE=3b,则AD=2a,OE=2b,=,
∴OD=5b,BD=,∴AB=AD+DB=.
∵S△ABC=AB·OD=××5b=13,
∴ab=,∴S矩形ODBF=BD·OD=·5b==18.
又∵反比例函数y=(x>0)的图象在第一象限,
∴k=18.
三、13.解:设===k,则x=3k,y=4k,z=5k,
∵2x+y+z=45,∴2×3k+4k+5k=45,
解得k=3,∴x=9,y=12,z=15,
∴3x+2y-z=3×9+2×12-15=27+24-15=36.
14.解:(1)2∶1; A
(2)△AEE′是△ABB′的位似图形,
相似比为EE′∶BB′=4∶1;
(3)存在,符合条件的三角形是△ADD′.
15.证明:∵D是△ABC的边AB的中点,∴AD=DB.
∵DE∥BC,∴==1,∴AF=FC.
∵CE∥AB,∴==1,
∴DF=EF,即F是DE的中点.
16.解:如图,过点A作AG⊥DE,交BC于点F,交DE于点G,则AF⊥BC.
INCLUDEPICTURE"DJ3-2.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\DJ3-2.tif" \* MERGEFORMATINET
(第16题)
∵BC∥ED,∴△ABC∽△ADE,
∴AF∶AG=BC∶DE.
∵AF=3m,FG=12m,∴AG=AF+FG=15m,
∴3∶15=10∶DE,∴DE=50m,
∴DE处共有50÷2+1=26(棵)树.
17.(1)证明:∵AD为∠BAC的平分线,
∴∠BAD=∠DAC.
∵∠EFD=∠BDF,∴∠AFE=∠ADC,
∴△AFE∽△ADC.
(2)解:∵△AFE∽△ADC,∴∠AEF=∠C.
∵∠AFE=∠C,∴∠AEF=∠AFE,∴AE=AF.
∵=,△AFE∽△ADC,
∴==,∴=4.
∵AE=2EB,AE=AF,∴==2,∴EB=2FD.
18.解:存在.当△ACD∽△MNA时,有=,
即=,∴36-12t=3t.∴t=2.4;
当△ACD∽△NMA时,有=,即=.
∴6t=18-6t.∴t=1.5.
综上,t=2.4或1.5.
PAGE
(限时: 120分钟 满分: 100分)
班级: 姓名: 得分:
一、选择题(每题3分,共18分)
1.下列四组线段中,是成比例线段的是( )
A.3,6,9,16 B.2,3,4,5
C.,,,5 D.5,2,3,6
2.如图,∠B=∠ACD,则哪条线段与AD的比等于△ABC与△ACD周长之比? ( )
A.BC B.AC
C.AB D.BD
INCLUDEPICTURE"J3-1.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J3-1.tif" \* MERGEFORMATINET INCLUDEPICTURE"J3-2.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J3-2.tif" \* MERGEFORMATINET INCLUDEPICTURE"J3-3.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J3-3.tif" \* MERGEFORMATINET INCLUDEPICTURE"J3-5.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J3-5.tif" \* MERGEFORMATINET
(第2题) (第3题) (第4题) (第6题)
3.如图,在△ABC中,点D,E分别在AB,AC边上,AD=2,AB=6,添加下列条件不—定能判定DE∥BC的是( )
A.= B.=
C.= D.=
4.如图,在平面直角坐标系中,△ABC与△DEF是以坐标原点O为位似中心的位似图形,若A(-2,0),D(3,0),且BC=3,则线段EF的长度为( )
A.2 B.4
C. D.6
5.已知点P是线段AB的黄金分割点,AP>PB,则AP∶PB的值为( )
A. B.-1
C.0.618 D.
6.如图,已知△ABC和△EDF的顶点都在正方形网格的格点上,则∠ABC+∠ACB的度数为( )
A.30° B.45°
C.60° D.75°
二、填空题(每题4分,共24分)
7.已知=,则=________.
8.如图,△ABC中,BC>BA,点D是BC边上的一个动点(点D与点B,C不重合),若再增加一个条件,就能使△ABD与△ABC相似,则这个条件可以是________(写出一个即可).
INCLUDEPICTURE"J3-6.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J3-6.tif" \* MERGEFORMATINET INCLUDEPICTURE"J3-7.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J3-7.tif" \* MERGEFORMATINET
(第8题) (第10题)
9.若△ABC∽△A′B′C′,且△ABC与△A′B′C′的面积之比为3∶4,则∠ABC与∠A′B′C′的平分线之比为________.
10.如图,已知AB∥CD∥EF,=,BE=15,那么CE的长为________.
11.如图,在△ABC与△DEF中,=,∠B=∠E, CM⊥AB,FN⊥DE,G、H分别是BC、EF的中点.若=,则=____________.
INCLUDEPICTURE"SXJ3-7.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\SXJ3-7.tif" \* MERGEFORMATINET INCLUDEPICTURE"J3-8.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J3-8.tif" \* MERGEFORMATINET
(第11题) (第12题)
12.如图,△ABC的顶点B在反比例函数y=(x>0)的图象上,顶点C在x轴负半轴上,AB∥x轴,AB,BC分别交y轴于点D,E.若==,S△ABC=13,则k=________.
三、解答题(13,14题每题8分,18题12分,其余每题10分,共58分)
13.已知==,2x+y+z=45,求代数式3x+2y-z的值.
14.如图,△ACC′是由△ABB′经过位似变换得到的.
(1)△ACC′与△ABB′的相似比为________,它们的位似中心是点________.
(2)△AEE′是△ABB′的位似图形吗?如果是,求相似比;如果不是,说明理由.
(3)图中是否存在一个三角形与△ABB′位似,且位似比为3∶1?如果存在,请写出符合条件的三角形;若不存在,说明理由.
INCLUDEPICTURE"J3-9.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J3-9.tif" \* MERGEFORMATINET
(第14题)
15.如图,D是△ABC的边AB的中点,DE∥BC,CE∥AB,AC与DE相交于点F.
求证:F是DE的中点.
INCLUDEPICTURE"J3-10.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J3-10.tif" \* MERGEFORMATINET
(第15题)
16.如图,某宣传栏BC后面12 m处有一排与宣传栏平行(即BC∥ED)的若干棵树,且相邻两棵树的间隔为2 m,某人站在距宣传栏3 m的A处,正好看到两端的树干,其余的树均被宣传栏挡住.已知BC=10 m,求该宣传栏后DE处共有多少棵树.(不计宣传栏的厚度)
INCLUDEPICTURE"J3-11.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J3-11.tif" \* MERGEFORMATINET
(第16题)
17.如图,在△ABC中,AD平分∠BAC,与BC相交于点D,点E,F分别在线段AB,AD上,且∠EFD=∠BDF.
(1)求证:△AFE∽△ADC.
(2)若=,AE=2EB,且∠AFE=∠C,试探究线段DF与BE之间的数量关系.
INCLUDEPICTURE"J3-12.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J3-12.tif" \* MERGEFORMATINET
(第17题)
18.如图,矩形ABCD中,AB=3cm,BC=6cm.某一时刻,动点M从点A出发沿AB方向以1cm/s的速度向点B匀速运动,同时动点N从点D出发沿DA方向以2cm/s的速度向点A匀速运动,设运动时间为t s.问是否存在t,使以A、M、N为顶点的三角形与△ACD相似?若存在,求出t的值;若不存在,请说明理由.
INCLUDEPICTURE"J3-13.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J3-13.tif" \* MERGEFORMATINET
(第18题)
答案
一、1.C 2.B 3.A 4.C 5.D 6.B
二、7.
8.(答案不唯一)∠BAD=∠C
9.
10.6 点拨:∵AB∥CD∥EF,∴=,即=,解得CE=6.
11.
12.18 点拨:如图,过点B作BF⊥x轴于点F.
∵AB∥x轴,∴△DBE∽△OCE,
INCLUDEPICTURE"DJ3-1.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\DJ3-1.tif" \* MERGEFORMATINET
(第12题)
∴==.
∵==,∴====,
设CO=3a,DE=3b,则AD=2a,OE=2b,=,
∴OD=5b,BD=,∴AB=AD+DB=.
∵S△ABC=AB·OD=××5b=13,
∴ab=,∴S矩形ODBF=BD·OD=·5b==18.
又∵反比例函数y=(x>0)的图象在第一象限,
∴k=18.
三、13.解:设===k,则x=3k,y=4k,z=5k,
∵2x+y+z=45,∴2×3k+4k+5k=45,
解得k=3,∴x=9,y=12,z=15,
∴3x+2y-z=3×9+2×12-15=27+24-15=36.
14.解:(1)2∶1; A
(2)△AEE′是△ABB′的位似图形,
相似比为EE′∶BB′=4∶1;
(3)存在,符合条件的三角形是△ADD′.
15.证明:∵D是△ABC的边AB的中点,∴AD=DB.
∵DE∥BC,∴==1,∴AF=FC.
∵CE∥AB,∴==1,
∴DF=EF,即F是DE的中点.
16.解:如图,过点A作AG⊥DE,交BC于点F,交DE于点G,则AF⊥BC.
INCLUDEPICTURE"DJ3-2.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\DJ3-2.tif" \* MERGEFORMATINET
(第16题)
∵BC∥ED,∴△ABC∽△ADE,
∴AF∶AG=BC∶DE.
∵AF=3m,FG=12m,∴AG=AF+FG=15m,
∴3∶15=10∶DE,∴DE=50m,
∴DE处共有50÷2+1=26(棵)树.
17.(1)证明:∵AD为∠BAC的平分线,
∴∠BAD=∠DAC.
∵∠EFD=∠BDF,∴∠AFE=∠ADC,
∴△AFE∽△ADC.
(2)解:∵△AFE∽△ADC,∴∠AEF=∠C.
∵∠AFE=∠C,∴∠AEF=∠AFE,∴AE=AF.
∵=,△AFE∽△ADC,
∴==,∴=4.
∵AE=2EB,AE=AF,∴==2,∴EB=2FD.
18.解:存在.当△ACD∽△MNA时,有=,
即=,∴36-12t=3t.∴t=2.4;
当△ACD∽△NMA时,有=,即=.
∴6t=18-6t.∴t=1.5.
综上,t=2.4或1.5.
PAGE
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
