湘教版九年级数学上册 第4章 锐角三角函数 达标检测卷(word版含答案)
文档属性
| 名称 | 湘教版九年级数学上册 第4章 锐角三角函数 达标检测卷(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 217.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 00:00:00 | ||
图片预览



文档简介
湘教版九年级数学上册 第4章 达标检测卷
(限时: 120分钟 满分: 100分)
班级: 姓名: 得分:
一、选择题(每题3分,共18分)
1.2sin 45°·cos 45°的值为( )
A.1 B. C. D.2
2.在Rt△ABC中,∠C=90°,∠A, ∠B, ∠C的对边分别为a,b,c,下列结论正确的是( )
A.sin A= B.cos B= C.tan A= D.tan B=
3.已知α为锐角,且cos(90°-α)=,则sin α的值为( )
A. B. C. D.
4.在Rt△ABC中,∠C=90°,∠A=60°,AC=6,则BC的长为( )
A.6 B.3 C.3 D.12
5.如图,以△AOC的顶点O为坐标原点,OC所在直线为x轴,建立平面直角坐标系,若∠AOC=α,AO=c,OC=a,AC=b,则点A的坐标是( )
A.(acos α,asin α) B.(ccos α,csin α)
C.(asin α,acos α) D.(csin α,ccos α)
INCLUDEPICTURE"J4-1.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J4-1.tif" \* MERGEFORMATINET INCLUDEPICTURE"SXJ4-4.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\SXJ4-4.tif" \* MERGEFORMATINET INCLUDEPICTURE"SXJ4-5.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\SXJ4-5.tif" \* MERGEFORMATINET INCLUDEPICTURE"J4-2.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J4-2.tif" \* MERGEFORMATINET
(第5题) (第6题) (第7题) (第8题)
6.如图,测绘师在离古塔10 m远的点C处测得塔顶A的仰角为α,他又在离古塔25 m远的点D处测得塔顶A的仰角为β,若tan α·tan β=1,点D,C,B在同一条直线上,则测绘师测得古塔的高度约为(参考数据:≈3.162)( )
A.15.81 m B.16.81 m C.30.62 m D.31.62 m
二、填空题(每题4分,共24分)
7.如图,方格纸中每个小正方形的边长都是1个单位长度,每个小正方形的顶点叫作格点.△ABC的顶点都在方格纸的格点上,则cos A=________.
8.如图,在△ABC中,∠B=30°,用直尺和圆规按照下列步骤作图:①分别以B、C两点为圆心,以大于BC的长为半径作弧,两弧交于两点;②过两弧的交点作直线,交AB于点D;③连接CD.则cos∠ADC=________.
9.如图,菱形ABCD的周长为20 cm,且tan∠ABD=,则菱形ABCD的面积为________.
INCLUDEPICTURE"SXJ4-8.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\SXJ4-8.tif" \* MERGEFORMATINET INCLUDEPICTURE"J4-3.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J4-3.tif" \* MERGEFORMATINET
(第9题) (第10题)
10.如图,一次函数y=ax+b的图象与反比例函数y=的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知OA=,tan∠AOC=,则反比例函数的表达式为________.
11.如图,在矩形ABCD中,过点D作DE⊥AC于点E,已知cos∠ADE=,AB=4,则对角线AC的长为________.
INCLUDEPICTURE"J4-4.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J4-4.tif" \* MERGEFORMATINET INCLUDEPICTURE"SXJ4-10.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\SXJ4-10.tif" \* MERGEFORMATINET
(第11题) (第12题)
12.如图,一艘货轮以18 km/h的速度在海面上沿正东方向航行,当行驶至A处时,发现它的东南方向有一灯塔B,货轮继续向东航行30 min后到达C处,发现灯塔B在它的南偏东15°方向,则此时货轮与灯塔B的距离是____________km.
三、解答题(13,14题每题8分,18题12分,其余每题10分,共58分)
13.计算:
(1)-(π-3.14)0+sin 30°+;
(2)tan 45°·sin 45°-2sin 30°·cos 45°+tan 30°.
14.如图,在Rt△ABC中,∠C=90°,tan A=,求∠B的正弦、余弦值.
INCLUDEPICTURE"J4-5.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J4-5.tif" \* MERGEFORMATINET
(第14题)
15.如图,在△ABC中,∠C=90°,BC=AC=7,D为BC上一点,sin∠DAB=,求线段BD的长.
INCLUDEPICTURE"J4-6.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J4-6.tif" \* MERGEFORMATINET
(第15题)
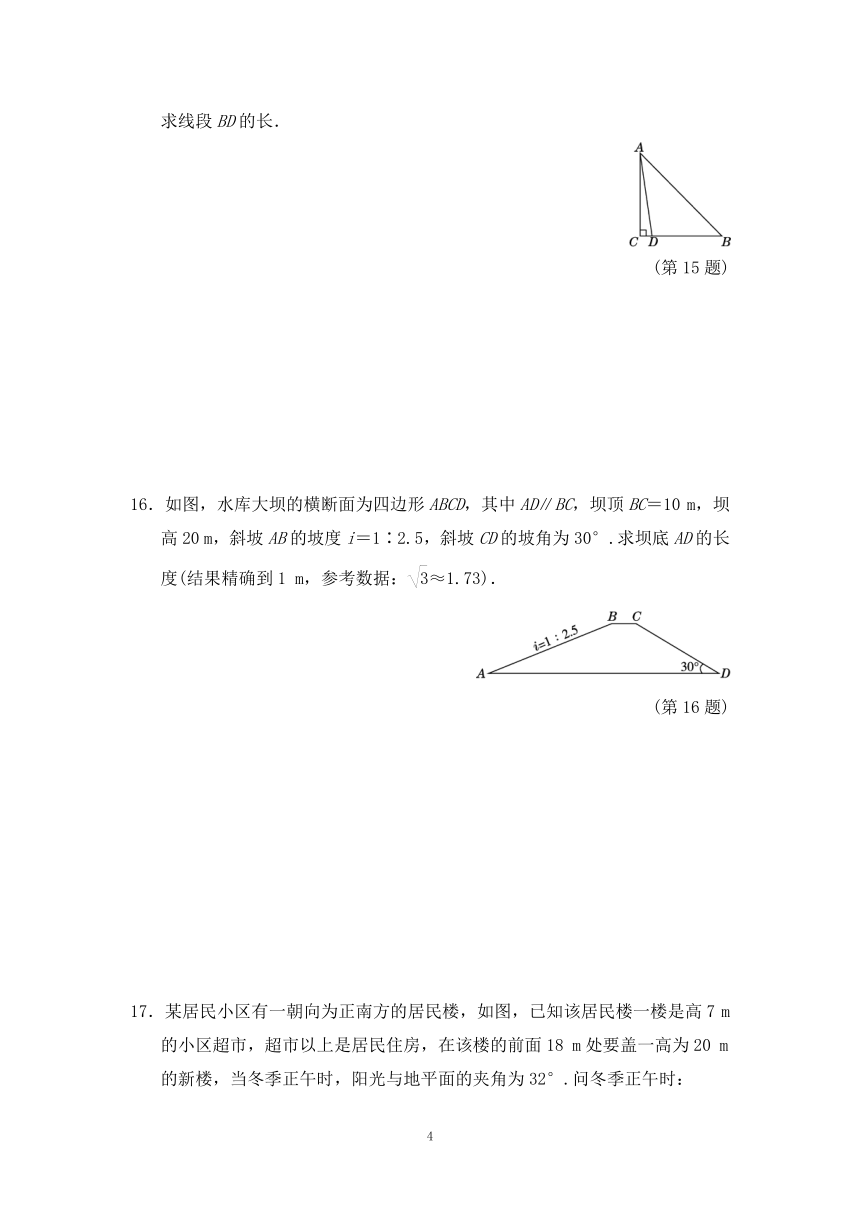
16.如图,水库大坝的横断面为四边形ABCD,其中AD∥BC,坝顶BC=10 m,坝高20 m,斜坡AB的坡度i=1∶2.5,斜坡CD的坡角为30°.求坝底AD的长度(结果精确到1 m,参考数据:≈1.73).
INCLUDEPICTURE"J4-7.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J4-7.tif" \* MERGEFORMATINET
(第16题)
17.某居民小区有一朝向为正南方的居民楼,如图,已知该居民楼一楼是高7 m的小区超市,超市以上是居民住房,在该楼的前面18 m处要盖一高为20 m的新楼,当冬季正午时,阳光与地平面的夹角为32°.问冬季正午时:
(1)超市以上的居民住房的采光是否受影响?
(2)若要使超市采光不受影响,两楼至少应相距________m.(结果保留整数,参考数据:tan 32°≈0.625)
INCLUDEPICTURE"J4-8.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J4-8.tif" \* MERGEFORMATINET
(第17题)
18.为了应对人口老龄化问题,国家大力发展养老事业.某养老机构定制轮椅供行动不便的老人使用.如图是一种型号的手动轮椅的侧面示意图,该轮椅前后长度为120 cm,后轮半径为24 cm,CB=CD=24 cm,踏板CB与CD垂直,横档AD、踏板CB与地面所成的角分别为15°、30°.求:
(1)横档AD的长;
(2)点C距地面的高度.(结果精确到1 cm,参考数据:sin 15°≈0.26,cos 15°≈0.97,≈1.73)
INCLUDEPICTURE"SXJ4-14.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\SXJ4-14.tif" \* MERGEFORMATINET
(第18题)
答案
一、1.A 2.B 3.C 4.A 5.B
6.A 点拨:∵BC=10 m,BD=25 m,
∴在Rt△ABC中,AB=BC·tan α=10tan α m,
在Rt△ABD中,AB=BD·tan β=25tan β m.
∵tan α·tan β=1,
∴AB2=10tan α·25tan β=250,
∴AB==5≈5×3.162=15.81(m).
二、7. 8.
9.24 cm2 点拨:连接AC交BD于点O,则AC⊥BD.
∵菱形ABCD的周长为20 cm,
∴菱形ABCD的边长为5 cm.
在Rt△ABO中,tan∠ABO==,
∴可设OA=4x cm,则OB=3x cm.
又∵AB=5 cm,∴易得OA=4 cm,OB=3 cm,
∴AC=8 cm,BD=6 cm,
∴菱形ABCD的面积为×6×8=24(cm2).
10.y=
11. 点拨:∵四边形ABCD是矩形,
∴∠ADC=90°,CD=AB=4,
∵DE⊥AC,∴∠DEC=90°,∴∠DCE+∠CDE=90°,
∵∠ADE+∠CDE=90°,∴∠ADE=∠DCE,
∴cos∠DCA=cos∠ADE==.
∵CD=4,∴AC=.
12.18
三、13.解:(1)原式=2--1+×2 +4=2--1++4=5.
(2)原式=1×-2××+=-+=.
14.解:∵tan A==,∴可设BC=x,则AC=2x,
∴AB=x,
∴sin B===,cos B===.
15.解:过点D作DE⊥AB,垂足为点E,
∴sin∠DAB==,∴可设DE=3x,则AD=5x,
∴AE=4x,BE=3x,∴AB=AE+BE=7x.
∵AC=BC=7,∠C=90°,
∴由勾股定理,得AB=7 ,
∴7x=7 ,∴x=,∴BE=DE=3 ,
∴BD==6.
16.解:作BE⊥AD于点E,CF⊥AD于点F,
则四边形BEFC是矩形,∴EF=BC=10 m.
∵BE=20 m,斜坡AB的坡度i=1∶2.5,
∴AE=50 m.∵CF=20 m,斜坡CD的坡角为30°,
∴DF==20 ≈35(m),
∴AD=AE+EF+FD≈95 m.
答:坝底AD的长度约为95 m.
17.解:(1)过点F作FE⊥AB于点E.
设CF=x m,则AE=(20-x)m,
由题意得tan∠AFE=tan 32°==,
∴x=20-18tan 32°≈9.
∵9>7,∴超市以上的居民住房的采光受影响.
(2)32
18.解:(1)如图,过点C作CG⊥BG于点G,过点D作DF∥BG交GC的延长线于点F,过点A作AE⊥DF于点E.
INCLUDEPICTURE"SXJD4-5.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\SXJD4-5.tif" \* MERGEFORMATINET
(第18题)
在Rt△DFC中,FC=DC·sin 30°=24×=12 (cm),DF=DC·cos 30°=24×=12 (cm).
在Rt△BCG中,CG=BC·cos 30°=24×=12 (cm),
∴AE=120-24-12-12 ≈63.2(cm).
在Rt△ADE中,AD=≈≈65(cm).
因此,横档AD的长约为65 cm.
(2)在Rt△ADE中,
DE=AD·sin 15°≈65×0.26=16.9 (cm),
∴点C距地面的高度为DE+24-DF≈16.9+24-12 ≈20(cm).
∴点C距地面的高度约为20 cm
PAGE
(限时: 120分钟 满分: 100分)
班级: 姓名: 得分:
一、选择题(每题3分,共18分)
1.2sin 45°·cos 45°的值为( )
A.1 B. C. D.2
2.在Rt△ABC中,∠C=90°,∠A, ∠B, ∠C的对边分别为a,b,c,下列结论正确的是( )
A.sin A= B.cos B= C.tan A= D.tan B=
3.已知α为锐角,且cos(90°-α)=,则sin α的值为( )
A. B. C. D.
4.在Rt△ABC中,∠C=90°,∠A=60°,AC=6,则BC的长为( )
A.6 B.3 C.3 D.12
5.如图,以△AOC的顶点O为坐标原点,OC所在直线为x轴,建立平面直角坐标系,若∠AOC=α,AO=c,OC=a,AC=b,则点A的坐标是( )
A.(acos α,asin α) B.(ccos α,csin α)
C.(asin α,acos α) D.(csin α,ccos α)
INCLUDEPICTURE"J4-1.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J4-1.tif" \* MERGEFORMATINET INCLUDEPICTURE"SXJ4-4.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\SXJ4-4.tif" \* MERGEFORMATINET INCLUDEPICTURE"SXJ4-5.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\SXJ4-5.tif" \* MERGEFORMATINET INCLUDEPICTURE"J4-2.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J4-2.tif" \* MERGEFORMATINET
(第5题) (第6题) (第7题) (第8题)
6.如图,测绘师在离古塔10 m远的点C处测得塔顶A的仰角为α,他又在离古塔25 m远的点D处测得塔顶A的仰角为β,若tan α·tan β=1,点D,C,B在同一条直线上,则测绘师测得古塔的高度约为(参考数据:≈3.162)( )
A.15.81 m B.16.81 m C.30.62 m D.31.62 m
二、填空题(每题4分,共24分)
7.如图,方格纸中每个小正方形的边长都是1个单位长度,每个小正方形的顶点叫作格点.△ABC的顶点都在方格纸的格点上,则cos A=________.
8.如图,在△ABC中,∠B=30°,用直尺和圆规按照下列步骤作图:①分别以B、C两点为圆心,以大于BC的长为半径作弧,两弧交于两点;②过两弧的交点作直线,交AB于点D;③连接CD.则cos∠ADC=________.
9.如图,菱形ABCD的周长为20 cm,且tan∠ABD=,则菱形ABCD的面积为________.
INCLUDEPICTURE"SXJ4-8.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\SXJ4-8.tif" \* MERGEFORMATINET INCLUDEPICTURE"J4-3.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J4-3.tif" \* MERGEFORMATINET
(第9题) (第10题)
10.如图,一次函数y=ax+b的图象与反比例函数y=的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知OA=,tan∠AOC=,则反比例函数的表达式为________.
11.如图,在矩形ABCD中,过点D作DE⊥AC于点E,已知cos∠ADE=,AB=4,则对角线AC的长为________.
INCLUDEPICTURE"J4-4.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J4-4.tif" \* MERGEFORMATINET INCLUDEPICTURE"SXJ4-10.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\SXJ4-10.tif" \* MERGEFORMATINET
(第11题) (第12题)
12.如图,一艘货轮以18 km/h的速度在海面上沿正东方向航行,当行驶至A处时,发现它的东南方向有一灯塔B,货轮继续向东航行30 min后到达C处,发现灯塔B在它的南偏东15°方向,则此时货轮与灯塔B的距离是____________km.
三、解答题(13,14题每题8分,18题12分,其余每题10分,共58分)
13.计算:
(1)-(π-3.14)0+sin 30°+;
(2)tan 45°·sin 45°-2sin 30°·cos 45°+tan 30°.
14.如图,在Rt△ABC中,∠C=90°,tan A=,求∠B的正弦、余弦值.
INCLUDEPICTURE"J4-5.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J4-5.tif" \* MERGEFORMATINET
(第14题)
15.如图,在△ABC中,∠C=90°,BC=AC=7,D为BC上一点,sin∠DAB=,求线段BD的长.
INCLUDEPICTURE"J4-6.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J4-6.tif" \* MERGEFORMATINET
(第15题)
16.如图,水库大坝的横断面为四边形ABCD,其中AD∥BC,坝顶BC=10 m,坝高20 m,斜坡AB的坡度i=1∶2.5,斜坡CD的坡角为30°.求坝底AD的长度(结果精确到1 m,参考数据:≈1.73).
INCLUDEPICTURE"J4-7.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J4-7.tif" \* MERGEFORMATINET
(第16题)
17.某居民小区有一朝向为正南方的居民楼,如图,已知该居民楼一楼是高7 m的小区超市,超市以上是居民住房,在该楼的前面18 m处要盖一高为20 m的新楼,当冬季正午时,阳光与地平面的夹角为32°.问冬季正午时:
(1)超市以上的居民住房的采光是否受影响?
(2)若要使超市采光不受影响,两楼至少应相距________m.(结果保留整数,参考数据:tan 32°≈0.625)
INCLUDEPICTURE"J4-8.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\J4-8.tif" \* MERGEFORMATINET
(第17题)
18.为了应对人口老龄化问题,国家大力发展养老事业.某养老机构定制轮椅供行动不便的老人使用.如图是一种型号的手动轮椅的侧面示意图,该轮椅前后长度为120 cm,后轮半径为24 cm,CB=CD=24 cm,踏板CB与CD垂直,横档AD、踏板CB与地面所成的角分别为15°、30°.求:
(1)横档AD的长;
(2)点C距地面的高度.(结果精确到1 cm,参考数据:sin 15°≈0.26,cos 15°≈0.97,≈1.73)
INCLUDEPICTURE"SXJ4-14.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\SXJ4-14.tif" \* MERGEFORMATINET
(第18题)
答案
一、1.A 2.B 3.C 4.A 5.B
6.A 点拨:∵BC=10 m,BD=25 m,
∴在Rt△ABC中,AB=BC·tan α=10tan α m,
在Rt△ABD中,AB=BD·tan β=25tan β m.
∵tan α·tan β=1,
∴AB2=10tan α·25tan β=250,
∴AB==5≈5×3.162=15.81(m).
二、7. 8.
9.24 cm2 点拨:连接AC交BD于点O,则AC⊥BD.
∵菱形ABCD的周长为20 cm,
∴菱形ABCD的边长为5 cm.
在Rt△ABO中,tan∠ABO==,
∴可设OA=4x cm,则OB=3x cm.
又∵AB=5 cm,∴易得OA=4 cm,OB=3 cm,
∴AC=8 cm,BD=6 cm,
∴菱形ABCD的面积为×6×8=24(cm2).
10.y=
11. 点拨:∵四边形ABCD是矩形,
∴∠ADC=90°,CD=AB=4,
∵DE⊥AC,∴∠DEC=90°,∴∠DCE+∠CDE=90°,
∵∠ADE+∠CDE=90°,∴∠ADE=∠DCE,
∴cos∠DCA=cos∠ADE==.
∵CD=4,∴AC=.
12.18
三、13.解:(1)原式=2--1+×2 +4=2--1++4=5.
(2)原式=1×-2××+=-+=.
14.解:∵tan A==,∴可设BC=x,则AC=2x,
∴AB=x,
∴sin B===,cos B===.
15.解:过点D作DE⊥AB,垂足为点E,
∴sin∠DAB==,∴可设DE=3x,则AD=5x,
∴AE=4x,BE=3x,∴AB=AE+BE=7x.
∵AC=BC=7,∠C=90°,
∴由勾股定理,得AB=7 ,
∴7x=7 ,∴x=,∴BE=DE=3 ,
∴BD==6.
16.解:作BE⊥AD于点E,CF⊥AD于点F,
则四边形BEFC是矩形,∴EF=BC=10 m.
∵BE=20 m,斜坡AB的坡度i=1∶2.5,
∴AE=50 m.∵CF=20 m,斜坡CD的坡角为30°,
∴DF==20 ≈35(m),
∴AD=AE+EF+FD≈95 m.
答:坝底AD的长度约为95 m.
17.解:(1)过点F作FE⊥AB于点E.
设CF=x m,则AE=(20-x)m,
由题意得tan∠AFE=tan 32°==,
∴x=20-18tan 32°≈9.
∵9>7,∴超市以上的居民住房的采光受影响.
(2)32
18.解:(1)如图,过点C作CG⊥BG于点G,过点D作DF∥BG交GC的延长线于点F,过点A作AE⊥DF于点E.
INCLUDEPICTURE"SXJD4-5.tif" INCLUDEPICTURE "F:\\22秋\\9数XJ\\文件\\SXJD4-5.tif" \* MERGEFORMATINET
(第18题)
在Rt△DFC中,FC=DC·sin 30°=24×=12 (cm),DF=DC·cos 30°=24×=12 (cm).
在Rt△BCG中,CG=BC·cos 30°=24×=12 (cm),
∴AE=120-24-12-12 ≈63.2(cm).
在Rt△ADE中,AD=≈≈65(cm).
因此,横档AD的长约为65 cm.
(2)在Rt△ADE中,
DE=AD·sin 15°≈65×0.26=16.9 (cm),
∴点C距地面的高度为DE+24-DF≈16.9+24-12 ≈20(cm).
∴点C距地面的高度约为20 cm
PAGE
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
