沪科版九年级数学上册 第21章 二次函数与反比例函数 达标检测卷(word版含答案)
文档属性
| 名称 | 沪科版九年级数学上册 第21章 二次函数与反比例函数 达标检测卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 308.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 14:14:11 | ||
图片预览




文档简介
沪科版九年级数学上册 第21章 达标检测卷
(限时: 120分钟 满分: 150分)
班级: 姓名: 得分:
一、选择题(本大题共10小题,每小题4分,共40分)
1.下列各式中,y一定是x的二次函数的个数为( )
①y=x2+2x+5;②y=-5+8x-x2;③y=(3x+2)·(4x-3)-12x2;④y=ax2+bx+c;⑤y=mx2+x;⑥y=bx2+1(b为常数,b≠0).
A.3 B.4 C.5 D.6
2.下列对二次函数y=2(x-1)2图象的描述,正确的是( )
A.开口向下
B.对称轴是y轴
C.在对称轴左侧,y随x的增大而增大
D.顶点坐标为(1,0)
3.将如图所示的抛物线向右平移1个单位,再向上平移3个单位后,得到的抛物线的表达式是( )
A.y=(x-1)2+1 B.y=(x+1)2+1
C.y=2(x-1)2+1 D.y=2(x+1)2+1
INCLUDEPICTURE "九年级上册 物理 化学baidu(荣德基)/卷+1.TIF" \* MERGEFORMAT INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+1.TIF" \* MERGEFORMATINET INCLUDEPICTURE "九年级上册 物理 化学baidu(荣德基)/卷+2.TIF" \* MERGEFORMAT INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+2.TIF" \* MERGEFORMATINET INCLUDEPICTURE "九年级上册 物理 化学baidu(荣德基)/B-71.TIF" \* MERGEFORMAT INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\B-71.TIF" \* MERGEFORMATINET
(第3题) (第4题) (第5题)
4.如图,一次函数y1=ax+b和反比例函数y2=的图象相交于A,B两点,则使y1>y2成立的x的取值范围是( )
A.-2C.x<-2或x>4 D.-24
5.如图,抛物线y=ax2+bx+c的对称轴为直线x=-1,与y轴交于(0,-6),则关于x的方程ax2+bx+c+6=0的解为( )
A.x1=x2=0 B.x1=0,x2=-2
C.x1=0,x2=-1 D.x1=-2,x2=1
6.已知二次函数y=(1-a)xa2-2,在其图象对称轴的左侧,y随x的增大而减小,则a的值为( )
A.2 B.±2 C.-2 D.0
7.已知一次函数y=-kx+k的图象如图所示,则二次函数y=-kx2-2x+k的图象大致是( )
INCLUDEPICTURE "九年级上册 物理 化学baidu(荣德基)/卷+8.TIF" \* MERGEFORMAT INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+8.TIF" \* MERGEFORMATINET INCLUDEPICTURE "九年级上册 物理 化学baidu(荣德基)/DF44.TIF" \* MERGEFORMAT INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\DF44.TIF" \* MERGEFORMATINET INCLUDEPICTURE "九年级上册 物理 化学baidu(荣德基)/卷+10.TIF" \* MERGEFORMAT INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+10.TIF" \* MERGEFORMATINET
(第7题) (第9题) (第10题)
8.已知点A(x1,3),B(x2,6)都在反比例函数y=-的图象上,则下列关系式一定正确的是( )
A.x19.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0)和B,与y轴交于点C.下列结论:①abc<0;②2a+b<0;③4a-2b+c>0;④3a+c>0.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
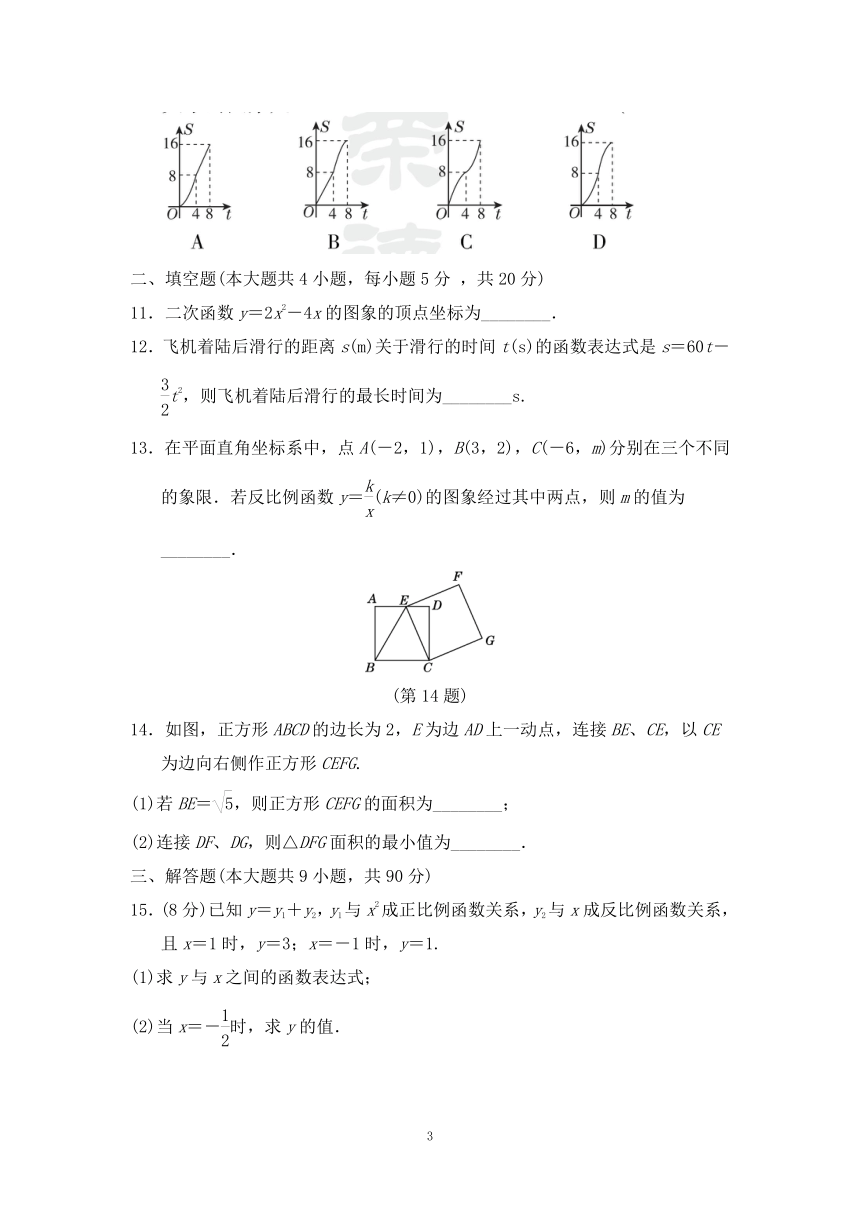
10.如图,在平面直角坐标系中,四边形OBCD是边长为4的正方形,平行于对角线BD的直线l从点O出发,沿x轴正方向以每秒1个单位的速度运动,运动到直线l与正方形没有交点为止.设直线l扫过正方形OBCD的面积为S,直线l运动的时间为t秒,下列能反映S与t之间函数关系的图象是( )
二、填空题(本大题共4小题,每小题5分 ,共20分)
11.二次函数y=2x2-4x的图象的顶点坐标为________.
12.飞机着陆后滑行的距离s(m)关于滑行的时间t(s)的函数表达式是s=60t-t2,则飞机着陆后滑行的最长时间为________s.
13.在平面直角坐标系中,点A(-2,1),B(3,2),C(-6,m)分别在三个不同的象限.若反比例函数y=(k≠0)的图象经过其中两点,则m的值为________.
INCLUDEPICTURE "九年级上册 物理 化学baidu(荣德基)/卷+15.TIF" \* MERGEFORMAT INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+15.TIF" \* MERGEFORMATINET
(第14题)
14.如图,正方形ABCD的边长为2,E为边AD上一动点,连接BE、CE,以CE为边向右侧作正方形CEFG.
(1)若BE=,则正方形CEFG的面积为________;
(2)连接DF、DG,则△DFG面积的最小值为________.
三、解答题(本大题共9小题,共90分)
15.(8分)已知y=y1+y2,y1与x2成正比例函数关系,y2与x成反比例函数关系,且x=1时,y=3;x=-1时,y=1.
(1)求y与x之间的函数表达式;
(2)当x=-时,求y的值.
16.(8分)已知抛物线y=ax2+bx+1经过点(1,-2),(-2,13).
(1)求a,b的值;
(2)若(5,y1),(m,y2)是抛物线上不同的两点,且y2=12-y1,求m的值.
17.(8分)已知反比例函数y=.
(1)如果这个函数的图象经过点(2,-1),求k的值;
(2)如果在这个函数图象所在的每个象限内,y的值随x值的增大而减小,求k的取值范围.
18.(8分)如图,一次函数y=kx+b与反比例函数y=(x>0)的图象交于A(m,4),B(2,n)两点,与坐标轴分别交于M、N两点.
(1)求一次函数的表达式;
(2)根据图象直接写出kx+b->0中x的取值范围;
(3)求△AOB的面积.
INCLUDEPICTURE "九年级上册 物理 化学baidu(荣德基)/卷+17.TIF" \* MERGEFORMAT INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+17.TIF" \* MERGEFORMATINET
(第18题)
19.(10分)暑假即将来临,青竹湖水上乐园的商家看准时机,购进一批单价为40元的儿童泳装,如果按单价60元销售,那么一个月内可售出240套.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,月销售量相应减少4套.设销售单价为x(60≤x≤75)元,月销售量为y套.
(1)求出y与x之间的函数表达式;
(2)商家一个月的盈利能达到6 800元吗?若能,求出此时的销售单价,若不能,求出最大月利润.
20.(10分)如图,开口向下的抛物线与x轴交于点A(-1,0)、B(2,0),与y轴交于点C(0,4),点P是第一象限内抛物线上的一点.
(1)求该抛物线的表达式;
(2)设四边形CABP的面积为S,求S的最大值.
INCLUDEPICTURE "九年级上册 物理 化学baidu(荣德基)/卷+18.TIF" \* MERGEFORMAT INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+18.TIF" \* MERGEFORMATINET
(第20题)
21.(12分)设二次函数y1,y2的图象的顶点分别为(a,b)、(c,d),当a=-2c,b=-2d,且开口方向相同时,则称y1是y2的“反倍顶二次函数”.
(1)请写出二次函数y=x2+x+1的一个“反倍顶二次函数”;
(2)已知关于x的二次函数y1=x2+nx和二次函数y2=x2-2nx+1,若函数y1恰是y1+y2的“反倍顶二次函数”,求n的值.
22.(12分)某景区平面图如图①所示,A、B、C、E、D为边界上的点,已知边界CED是一段抛物线,其余边界均为线段,且AD⊥AB,BC⊥AB,AD=BC=3,AB=8,抛物线顶点E到AB的距离OE=7,以AB所在直线为x轴,OE所在直线为y轴,建立平面直角坐标系.
(1)求边界CED所在抛物线的表达式;
(2)如图②,该景区管理处欲在区域ABCED内围成一个矩形场地MNPQ,使得点M、N在边界AB上,点P、Q在边界CED上,试确定点P的位置,使得矩形MNPQ的周长最大,并求出最大周长.
INCLUDEPICTURE "九年级上册 物理 化学baidu(荣德基)/卷+19.TIF" \* MERGEFORMAT INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+19.TIF" \* MERGEFORMATINET
(第22题)
23.(14分)如图,直线y=x-2与x、y轴分别交于点A、C.抛物线经过点A、C和点B(1,0).
(1)求抛物线的表达式和顶点G的坐标;
(2)在直线y=-1上是否存在点P,使得△PBG的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
INCLUDEPICTURE "九年级上册 物理 化学baidu(荣德基)/卷+20.TIF" \* MERGEFORMAT INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+20.TIF" \* MERGEFORMATINET
(第23题)
答案
一、1.A 2.D 3.C 4.B 5.B
6.C 7.B 8.A 9.B
10.D 点拨:①当0≤t≤4时,S=×t×t=t2,即S=t2,该函数图象是开口向上的抛物线的一部分,故B、C错误;②当4二、11.(1,-2) 12.20 13.-1
14.(1)5 (2) 点拨:(1)∵四边形ABCD是正方形,
∴AB=AD=CD=2,
∠A=∠D=90°.
∵BE=,∴AE===1.
∴DE=AD-AE=2-1=1.
∴EC2=DE2+CD2=12+22=5.
∴正方形CEFG的面积为5.
(2)设DE=x,则CE=.
易知S△DEC+S△DFG=S正方形CEFG,
∴S△DFG=(x2+4)-×x×2=x2-x+2=(x-1)2+.
∵>0,∴x=1时,△DFG面积的最小值为.
三、15.解:(1)可设y1=k1x2(k1≠0),y2=(k2≠0),则y=y1+y2=k1x2+,把x=1,y=3;x=-1,y=1分别代入上式,得解得
所以y=2x2+.
(2)当x=-时,y=2×+=-.
16.解:(1)把点(1,-2),(-2,13)的坐标代入y=ax2+bx+1,得解得
(2)由(1)得y=x2-4x+1,把x=5代入,得y1=6,
所以y2=12-y1=6.
所以y1=y2.
又易知对称轴为直线x=2,
所以5-2=2-m,解得m=-1.
17.解:(1)把点(2,-1)的坐标代入y=,得-1=,
解得k=-.
(2)因为在这个函数图象所在的每个象限内,y的值随x值的增大而减小,所以2k+1>0,解得k>-.
18.解:(1)因为点A在反比例函数y=的图象上,所以=4,解得m=1.所以点A的坐标为(1,4).因为点B也在反比例函数y=的图象上,所以=n,解得n=2.所以点B的坐标为(2,2).因为点A,B在y=kx+b的图象上,
所以解得
所以一次函数的表达式为y=-2x+6.
(2)x的取值范围为1(3)因为直线y=-2x+6与x轴的交点为N,
所以点N的坐标为(3,0).所以S△AOB=S△AON-S△BON=×3×4-×3×2=3.
19.解:(1)y=240-(x-60)×4=-4x+480(60≤x≤75).
(2)设一个月内获得的利润为w元,根据题意,得
w=(x-40)(-4x+480)=-4x2+640x-19 200=-4(x-80)2+6 400.因为-4<0,所以当x≤80时,w随x的增大而增大.因为60≤x≤75,
所以当x=75时,w有最大值,w最大值=-4×(75-80)2+6 400=6 300,
所以商家一个月的盈利不能达到6 800元,当销售单价为75元时,最大月利润是6 300元.
20.解:(1)设抛物线的表达式为y=a(x+1)(x-2),将点C(0,4)的坐标代入得4=-2a,解得a=-2,所以该抛物线的表达式为y=-2(x+1)(x-2)=-2x2+2x+4.
(2)连接OP,设点P的坐标为(m,-2m2+2m+4)(m>0),
易知OA=1,OC=4,OB=2,
所以S=S△OAC+S△OCP+S△OPB=×1×4+×4m+×2×(-2m2+2m+4)=-2m2+4m+6=-2(m-1)2+8,所以当m=1时,S最大,最大值为8.
21.解:(1)二次函数y=x2+x+1的一个“反倍顶二次函数”的表达式为y=(x-1)2-=x2-2x-.(答案不唯一)
(2)y1=x2+nx=-,图象的顶点坐标为,y1+y2=x2+nx+x2-2nx+1=2x2-nx+1=2+1-,顶点坐标为,由于函数y1恰是y1+y2的“反倍顶二次函数”,因此-=-2×,解得n=±2.
22.解:(1)设抛物线的表达式为y=ax2+7,易知点C的坐标为(4,3),将点C的坐标代入求得a=-,所以y=-x2+7.
(2)设P(0则PQ=MN=2m,PN=QM=-m2+7,
所以C矩形MNPQ=2=-(m-4)2+22(023.解:(1)在y=x-2中,令x=0,得y=-2;令y=0,得x=4.
所以A(4,0),C(0,-2).设抛物线的表达式为y=ax2+bx+c,
因为点A(4,0),B(1,0),C(0,-2)在抛物线上,所以
解得所以抛物线的表达式为y=-x2+x-2.
所以顶点G的坐标为.
(2)在直线y=-1上存在点P,使得△PBG的周长最小.作点B关于直线y=-1的对称点H(1,-2),连接GH交直线y=-1于点P,则点P为所求点.
所以C△PBG=BG+BP+PG=BG+PH+PG=GH+GB为最小.由点H,G的坐标,得直线HG的表达式为y=x-,当y=-1时,-1=x-,解得x=,故点P的坐标为.
PAGE
(限时: 120分钟 满分: 150分)
班级: 姓名: 得分:
一、选择题(本大题共10小题,每小题4分,共40分)
1.下列各式中,y一定是x的二次函数的个数为( )
①y=x2+2x+5;②y=-5+8x-x2;③y=(3x+2)·(4x-3)-12x2;④y=ax2+bx+c;⑤y=mx2+x;⑥y=bx2+1(b为常数,b≠0).
A.3 B.4 C.5 D.6
2.下列对二次函数y=2(x-1)2图象的描述,正确的是( )
A.开口向下
B.对称轴是y轴
C.在对称轴左侧,y随x的增大而增大
D.顶点坐标为(1,0)
3.将如图所示的抛物线向右平移1个单位,再向上平移3个单位后,得到的抛物线的表达式是( )
A.y=(x-1)2+1 B.y=(x+1)2+1
C.y=2(x-1)2+1 D.y=2(x+1)2+1
INCLUDEPICTURE "九年级上册 物理 化学baidu(荣德基)/卷+1.TIF" \* MERGEFORMAT INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+1.TIF" \* MERGEFORMATINET INCLUDEPICTURE "九年级上册 物理 化学baidu(荣德基)/卷+2.TIF" \* MERGEFORMAT INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+2.TIF" \* MERGEFORMATINET INCLUDEPICTURE "九年级上册 物理 化学baidu(荣德基)/B-71.TIF" \* MERGEFORMAT INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\B-71.TIF" \* MERGEFORMATINET
(第3题) (第4题) (第5题)
4.如图,一次函数y1=ax+b和反比例函数y2=的图象相交于A,B两点,则使y1>y2成立的x的取值范围是( )
A.-2
5.如图,抛物线y=ax2+bx+c的对称轴为直线x=-1,与y轴交于(0,-6),则关于x的方程ax2+bx+c+6=0的解为( )
A.x1=x2=0 B.x1=0,x2=-2
C.x1=0,x2=-1 D.x1=-2,x2=1
6.已知二次函数y=(1-a)xa2-2,在其图象对称轴的左侧,y随x的增大而减小,则a的值为( )
A.2 B.±2 C.-2 D.0
7.已知一次函数y=-kx+k的图象如图所示,则二次函数y=-kx2-2x+k的图象大致是( )
INCLUDEPICTURE "九年级上册 物理 化学baidu(荣德基)/卷+8.TIF" \* MERGEFORMAT INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+8.TIF" \* MERGEFORMATINET INCLUDEPICTURE "九年级上册 物理 化学baidu(荣德基)/DF44.TIF" \* MERGEFORMAT INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\DF44.TIF" \* MERGEFORMATINET INCLUDEPICTURE "九年级上册 物理 化学baidu(荣德基)/卷+10.TIF" \* MERGEFORMAT INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+10.TIF" \* MERGEFORMATINET
(第7题) (第9题) (第10题)
8.已知点A(x1,3),B(x2,6)都在反比例函数y=-的图象上,则下列关系式一定正确的是( )
A.x1
A.1个 B.2个 C.3个 D.4个
10.如图,在平面直角坐标系中,四边形OBCD是边长为4的正方形,平行于对角线BD的直线l从点O出发,沿x轴正方向以每秒1个单位的速度运动,运动到直线l与正方形没有交点为止.设直线l扫过正方形OBCD的面积为S,直线l运动的时间为t秒,下列能反映S与t之间函数关系的图象是( )
二、填空题(本大题共4小题,每小题5分 ,共20分)
11.二次函数y=2x2-4x的图象的顶点坐标为________.
12.飞机着陆后滑行的距离s(m)关于滑行的时间t(s)的函数表达式是s=60t-t2,则飞机着陆后滑行的最长时间为________s.
13.在平面直角坐标系中,点A(-2,1),B(3,2),C(-6,m)分别在三个不同的象限.若反比例函数y=(k≠0)的图象经过其中两点,则m的值为________.
INCLUDEPICTURE "九年级上册 物理 化学baidu(荣德基)/卷+15.TIF" \* MERGEFORMAT INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+15.TIF" \* MERGEFORMATINET
(第14题)
14.如图,正方形ABCD的边长为2,E为边AD上一动点,连接BE、CE,以CE为边向右侧作正方形CEFG.
(1)若BE=,则正方形CEFG的面积为________;
(2)连接DF、DG,则△DFG面积的最小值为________.
三、解答题(本大题共9小题,共90分)
15.(8分)已知y=y1+y2,y1与x2成正比例函数关系,y2与x成反比例函数关系,且x=1时,y=3;x=-1时,y=1.
(1)求y与x之间的函数表达式;
(2)当x=-时,求y的值.
16.(8分)已知抛物线y=ax2+bx+1经过点(1,-2),(-2,13).
(1)求a,b的值;
(2)若(5,y1),(m,y2)是抛物线上不同的两点,且y2=12-y1,求m的值.
17.(8分)已知反比例函数y=.
(1)如果这个函数的图象经过点(2,-1),求k的值;
(2)如果在这个函数图象所在的每个象限内,y的值随x值的增大而减小,求k的取值范围.
18.(8分)如图,一次函数y=kx+b与反比例函数y=(x>0)的图象交于A(m,4),B(2,n)两点,与坐标轴分别交于M、N两点.
(1)求一次函数的表达式;
(2)根据图象直接写出kx+b->0中x的取值范围;
(3)求△AOB的面积.
INCLUDEPICTURE "九年级上册 物理 化学baidu(荣德基)/卷+17.TIF" \* MERGEFORMAT INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+17.TIF" \* MERGEFORMATINET
(第18题)
19.(10分)暑假即将来临,青竹湖水上乐园的商家看准时机,购进一批单价为40元的儿童泳装,如果按单价60元销售,那么一个月内可售出240套.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,月销售量相应减少4套.设销售单价为x(60≤x≤75)元,月销售量为y套.
(1)求出y与x之间的函数表达式;
(2)商家一个月的盈利能达到6 800元吗?若能,求出此时的销售单价,若不能,求出最大月利润.
20.(10分)如图,开口向下的抛物线与x轴交于点A(-1,0)、B(2,0),与y轴交于点C(0,4),点P是第一象限内抛物线上的一点.
(1)求该抛物线的表达式;
(2)设四边形CABP的面积为S,求S的最大值.
INCLUDEPICTURE "九年级上册 物理 化学baidu(荣德基)/卷+18.TIF" \* MERGEFORMAT INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+18.TIF" \* MERGEFORMATINET
(第20题)
21.(12分)设二次函数y1,y2的图象的顶点分别为(a,b)、(c,d),当a=-2c,b=-2d,且开口方向相同时,则称y1是y2的“反倍顶二次函数”.
(1)请写出二次函数y=x2+x+1的一个“反倍顶二次函数”;
(2)已知关于x的二次函数y1=x2+nx和二次函数y2=x2-2nx+1,若函数y1恰是y1+y2的“反倍顶二次函数”,求n的值.
22.(12分)某景区平面图如图①所示,A、B、C、E、D为边界上的点,已知边界CED是一段抛物线,其余边界均为线段,且AD⊥AB,BC⊥AB,AD=BC=3,AB=8,抛物线顶点E到AB的距离OE=7,以AB所在直线为x轴,OE所在直线为y轴,建立平面直角坐标系.
(1)求边界CED所在抛物线的表达式;
(2)如图②,该景区管理处欲在区域ABCED内围成一个矩形场地MNPQ,使得点M、N在边界AB上,点P、Q在边界CED上,试确定点P的位置,使得矩形MNPQ的周长最大,并求出最大周长.
INCLUDEPICTURE "九年级上册 物理 化学baidu(荣德基)/卷+19.TIF" \* MERGEFORMAT INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+19.TIF" \* MERGEFORMATINET
(第22题)
23.(14分)如图,直线y=x-2与x、y轴分别交于点A、C.抛物线经过点A、C和点B(1,0).
(1)求抛物线的表达式和顶点G的坐标;
(2)在直线y=-1上是否存在点P,使得△PBG的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
INCLUDEPICTURE "九年级上册 物理 化学baidu(荣德基)/卷+20.TIF" \* MERGEFORMAT INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+20.TIF" \* MERGEFORMATINET
(第23题)
答案
一、1.A 2.D 3.C 4.B 5.B
6.C 7.B 8.A 9.B
10.D 点拨:①当0≤t≤4时,S=×t×t=t2,即S=t2,该函数图象是开口向上的抛物线的一部分,故B、C错误;②当4
14.(1)5 (2) 点拨:(1)∵四边形ABCD是正方形,
∴AB=AD=CD=2,
∠A=∠D=90°.
∵BE=,∴AE===1.
∴DE=AD-AE=2-1=1.
∴EC2=DE2+CD2=12+22=5.
∴正方形CEFG的面积为5.
(2)设DE=x,则CE=.
易知S△DEC+S△DFG=S正方形CEFG,
∴S△DFG=(x2+4)-×x×2=x2-x+2=(x-1)2+.
∵>0,∴x=1时,△DFG面积的最小值为.
三、15.解:(1)可设y1=k1x2(k1≠0),y2=(k2≠0),则y=y1+y2=k1x2+,把x=1,y=3;x=-1,y=1分别代入上式,得解得
所以y=2x2+.
(2)当x=-时,y=2×+=-.
16.解:(1)把点(1,-2),(-2,13)的坐标代入y=ax2+bx+1,得解得
(2)由(1)得y=x2-4x+1,把x=5代入,得y1=6,
所以y2=12-y1=6.
所以y1=y2.
又易知对称轴为直线x=2,
所以5-2=2-m,解得m=-1.
17.解:(1)把点(2,-1)的坐标代入y=,得-1=,
解得k=-.
(2)因为在这个函数图象所在的每个象限内,y的值随x值的增大而减小,所以2k+1>0,解得k>-.
18.解:(1)因为点A在反比例函数y=的图象上,所以=4,解得m=1.所以点A的坐标为(1,4).因为点B也在反比例函数y=的图象上,所以=n,解得n=2.所以点B的坐标为(2,2).因为点A,B在y=kx+b的图象上,
所以解得
所以一次函数的表达式为y=-2x+6.
(2)x的取值范围为1
所以点N的坐标为(3,0).所以S△AOB=S△AON-S△BON=×3×4-×3×2=3.
19.解:(1)y=240-(x-60)×4=-4x+480(60≤x≤75).
(2)设一个月内获得的利润为w元,根据题意,得
w=(x-40)(-4x+480)=-4x2+640x-19 200=-4(x-80)2+6 400.因为-4<0,所以当x≤80时,w随x的增大而增大.因为60≤x≤75,
所以当x=75时,w有最大值,w最大值=-4×(75-80)2+6 400=6 300,
所以商家一个月的盈利不能达到6 800元,当销售单价为75元时,最大月利润是6 300元.
20.解:(1)设抛物线的表达式为y=a(x+1)(x-2),将点C(0,4)的坐标代入得4=-2a,解得a=-2,所以该抛物线的表达式为y=-2(x+1)(x-2)=-2x2+2x+4.
(2)连接OP,设点P的坐标为(m,-2m2+2m+4)(m>0),
易知OA=1,OC=4,OB=2,
所以S=S△OAC+S△OCP+S△OPB=×1×4+×4m+×2×(-2m2+2m+4)=-2m2+4m+6=-2(m-1)2+8,所以当m=1时,S最大,最大值为8.
21.解:(1)二次函数y=x2+x+1的一个“反倍顶二次函数”的表达式为y=(x-1)2-=x2-2x-.(答案不唯一)
(2)y1=x2+nx=-,图象的顶点坐标为,y1+y2=x2+nx+x2-2nx+1=2x2-nx+1=2+1-,顶点坐标为,由于函数y1恰是y1+y2的“反倍顶二次函数”,因此-=-2×,解得n=±2.
22.解:(1)设抛物线的表达式为y=ax2+7,易知点C的坐标为(4,3),将点C的坐标代入求得a=-,所以y=-x2+7.
(2)设P(0
所以C矩形MNPQ=2=-(m-4)2+22(0
所以A(4,0),C(0,-2).设抛物线的表达式为y=ax2+bx+c,
因为点A(4,0),B(1,0),C(0,-2)在抛物线上,所以
解得所以抛物线的表达式为y=-x2+x-2.
所以顶点G的坐标为.
(2)在直线y=-1上存在点P,使得△PBG的周长最小.作点B关于直线y=-1的对称点H(1,-2),连接GH交直线y=-1于点P,则点P为所求点.
所以C△PBG=BG+BP+PG=BG+PH+PG=GH+GB为最小.由点H,G的坐标,得直线HG的表达式为y=x-,当y=-1时,-1=x-,解得x=,故点P的坐标为.
PAGE
