沪科版九年级数学上册 第22章 相似形 达标检测卷(word版含答案)
文档属性
| 名称 | 沪科版九年级数学上册 第22章 相似形 达标检测卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 283.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 14:14:41 | ||
图片预览




文档简介
沪科版九年级数学上册 第22章 达标检测卷
(限时: 120分钟 满分: 150分)
班级: 姓名: 得分:
一、选择题(本大题共10小题,每小题4分,共40分)
1.若2a-3b=0,则等于( )
A. B.- C. D.-
2.下列各组线段中,是成比例线段的一组是( )
A.a=4,b=6,c=5,d=10
B.a=2,b=4,c=3,d=6
C.a=2,b=,c=2 ,d=10
D.a=0.8,b=3,c=1,d=10
3.如图,在△ABC中,DE∥BC,AD=2,BD=3,AC=10,则AE的长为( )
A.3 B.4 C.5 D.6
INCLUDEPICTURE"卷+21.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+21.TIF" \* MERGEFORMATINET INCLUDEPICTURE"卷+22.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+22.TIF" \* MERGEFORMATINET INCLUDEPICTURE"卷+23.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+23.TIF" \* MERGEFORMATINET
(第3题) (第5题) (第6题)
4.已知线段AB=2,点P是线段AB的黄金分割点(AP>BP),则线段AP的长为( )
A.+1 B.-1
C. D.
5.如图,在△ABC中,点D、E分别在AB、AC边上,DE与BC不平行,那么下列条件中,不能判断△ADE∽△ACB的是( )
A.∠ADE=∠C B.∠AED=∠B
C.= D.=
6.如图,在△ABC中,AB∥DE,若=,则△ECD与△ACB的面积之比为( )
A. B. C. D.
7.如图,在△ABC中,D为AC边上一点,∠DBC=∠A,BC=,AC=3,则AD等于( )
A.2 B.1 C. D.
INCLUDEPICTURE"卷+16.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+16.TIF" \* MERGEFORMATINET INCLUDEPICTURE"卷+24.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+24.TIF" \* MERGEFORMATINET INCLUDEPICTURE"卷+25.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+25.TIF" \* MERGEFORMATINET
(第7题) (第8题) (第9题)
8.如图,在△ABC中,∠ACB=90°,AB=2,延长BC到点D,使BD=3CD,若E是AC的中点,则DE的长为( )
A. B. C. D.1
9.如图,△ABC中,CD⊥AB于D,①∠BCD=∠A;②AD∶AC=CD∶CB;③∠B+∠ACD=90°;④BC∶AC∶AB=3∶4∶5;⑤AC∶BD=AD∶CD.一定能确定△ABC为直角三角形的条件是( )
A.①②③ B.①②④
C.①②③④ D.③④⑤
10.如图,在△ACD中,AD=6,BC=5,AC2=AB(AB+BC),且△DAB∽△DCA,若AD=3AP,Q是线段AB上的动点,则PQ的最小值是( )
A. B. C. D.
INCLUDEPICTURE"卷+27.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+27.TIF" \* MERGEFORMATINET INCLUDEPICTURE"卷+28.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+28.TIF" \* MERGEFORMATINET
(第10题) (第12题)
二、填空题(本大题共4小题,每小题5分,共20分)
11.已知△ABC∽△A′B′C′,AD和A′D′是它们的对应中线,若AD=8,A′D′=6,则△ABC与△A′B′C′的周长比是________.
12.如图,在平面直角坐标系中,矩形OABC的顶点坐标分别是O(0,0),C(6,0),B(6,4),A(0,4),已知矩形OA′B′C′与矩形OABC位似,位似中心是原点O,且矩形OA′B′C′的面积等于矩形OABC面积的,则点B′的坐标是______________.
13.已知三角形纸片(△ABC)中,AB=AC=5,BC=8,将三角形按照如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是________.
INCLUDEPICTURE"卷+29.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+29.TIF" \* MERGEFORMATINET INCLUDEPICTURE"卷+30.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+30.TIF" \* MERGEFORMATINET
(第13题) (第14题)
14.如图,已知△ABC是等边三角形,点D,E,F分别是AB,AC,BC边上的点,∠EDF=120°,设=n.
(1)若n=1,则=________;
(2)若+=3,则n=________.
三、解答题(本大题共9小题,共90分)
15.(8分)已知:=.
(1)求的值;
(2)求的值.
16.(8分)如图,已知DE∥BC,FE∥CD,AF=3,AD=5,AE=4.
(1)求CE的长;
(2)求AB的长.
INCLUDEPICTURE"卷+31.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+31.TIF" \* MERGEFORMATINET
(第16题)
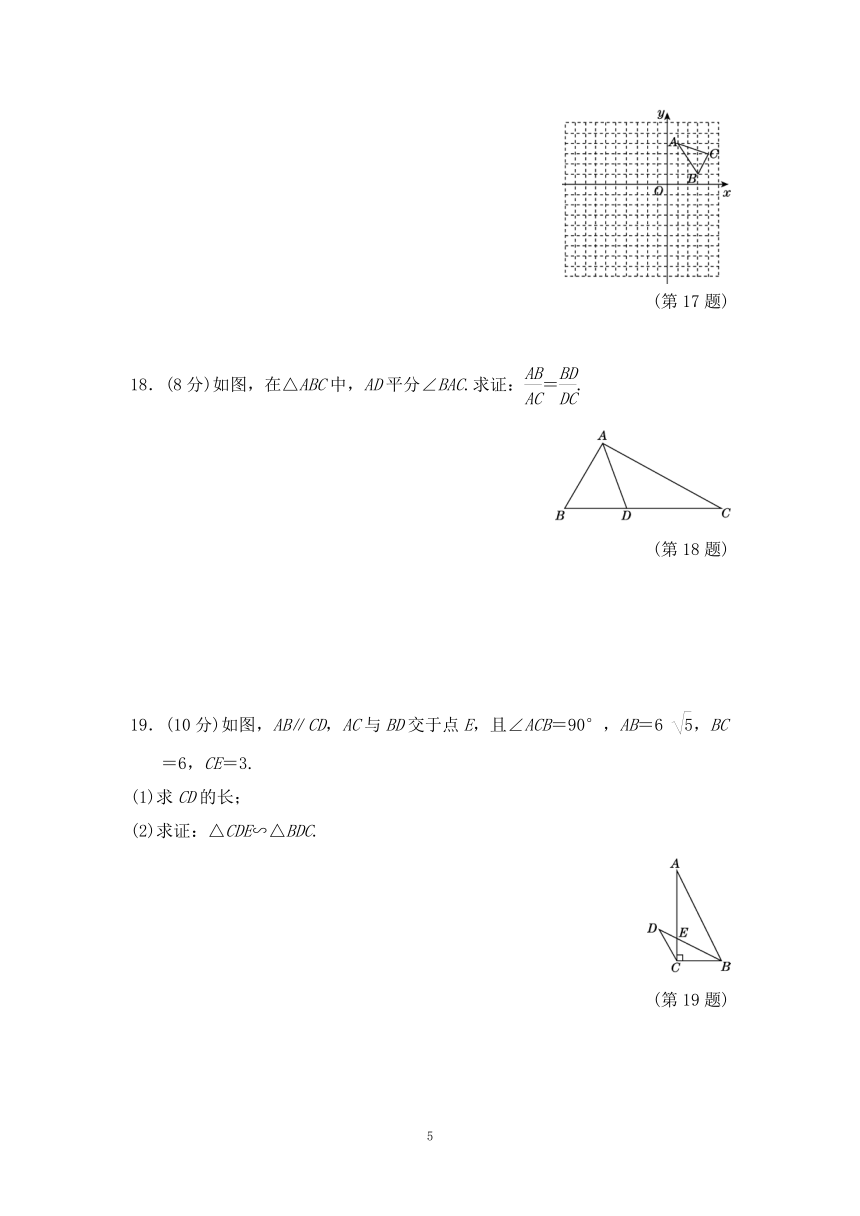
17.(8分)如图,在平面直角坐标系中,每个小正方形的边长都是1个单位,△ABC的顶点都在格点上.
(1)以原点O为位似中心,在第三象限内画出将△ABC放大为原来的2倍后的位似图形△A1B1C1;
(2)已知△ABC的面积为,则△A1B1C1的面积是______.
INCLUDEPICTURE"卷+32.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+32.TIF" \* MERGEFORMATINET
(第17题)
18.(8分)如图,在△ABC中,AD平分∠BAC.求证:=.
INCLUDEPICTURE"卷+33.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+33.TIF" \* MERGEFORMATINET
(第18题)
19.(10分)如图,AB∥CD,AC与BD交于点E,且∠ACB=90°,AB=6 ,BC=6,CE=3.
(1)求CD的长;
(2)求证:△CDE∽△BDC.
INCLUDEPICTURE"卷+34.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+34.TIF" \* MERGEFORMATINET
(第19题)
20.(10分)如图,在矩形ABCD中,E为DC上的一点,把△ADE沿AE翻折,使点D恰好落在BC边上的点F.
(1)求证:△ABF∽△FCE;
(2)若AB=2 ,AD=4,求CE的长.
INCLUDEPICTURE"卷+35.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+35.TIF" \* MERGEFORMATINET
(第20题)
21.(12分)如图,在△ABC中,点D、E分别在边BC、AC上,连接AD、DE,且∠B=∠ADE=∠C.
(1)求证:△BDA∽△CED;
(2)若∠B=45°,BC=6,当点D在BC上运动(点D不与B、C重合),且△ADE是等腰三角形时,求BD的长.
INCLUDEPICTURE"卷+36.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+36.TIF" \* MERGEFORMATINET
(第21题)
22.(12分)如图,矩形EFGH内接于△ABC(矩形各顶点在三角形边上),点E,F在BC上,点H,G分别在AB,AC上,且AD⊥BC于点D,交HG于点N.
(1)求证:△AHG∽△ABC;
(2)若AD=3,BC=9,设EH=x,矩形EFGH的面积为y,求出y与x之间的函数表达式,并写出自变量x的取值范围.
INCLUDEPICTURE"卷+37.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+37.TIF" \* MERGEFORMATINET
(第22题)
23.(14分)如图①,在正方形ABCD中,E为BC延长线上一点,且BC=3CE,F为CD的中点,EF的延长线交AD于点G,连接BG.
(1)求的值;
(2)求证:BG=EG;
(3)如图②,M为AB的中点,DM交BG于点N,连接CN,求证:CN∥GE.
INCLUDEPICTURE"卷+38.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+38.TIF" \* MERGEFORMATINET
(第23题)
答案
一、1.A 2.B 3.B 4.B 5.C
6.B 7.B 8.D 9.B
10.A 点拨:∵△DAB∽△DCA,
∴=,∴=.
解得BD=4(负值舍去).
∴===,
∴AC=AB.
∵AC2=AB(AB+BC),
∴=AB(AB+BC),解得AB=4,AB=0(舍去),
∴AB=BD=4.
过点B作BH⊥AD于点H,
∴AH=AD=3,
∴BH==.
∵AD=3AP,AD=6,∴AP=2.
当PQ⊥AB时,PQ的值最小,
∵∠AQP=∠AHB=90°,∠PAQ=∠BAH,
∴△APQ∽△ABH,
∴=,
∴=,∴PQ=.
二、11.4?3 12.(3,2)或(-3,-2)
13.
14.(1)1 (2)或
三、15.解:∵=,∴x=2y.
(1)==.
(2)==.
16.解:(1)∵FE∥CD,∴=.即=,解得AC=.
则CE=AC-AE=.
(2)∵DE∥BC,∴=.
即=,解得AB=.
17.解:(1)略 (2)14
18.证明:如图,过点B作BE∥AC,交线段AD的延长线于点E.
∵BE∥AC,∴△BDE∽△CDA.
∴∠BED=∠CAD,=.
∵AD平分∠BAC,
∴∠CAD=∠BAD,
∴∠BED=∠BAD.
∴AB=BE,∴=.
INCLUDEPICTURE"答卷+7.TIF" INCLUDEPICTURE "D:\\方正转Word\\9数HK安徽\\答卷+7.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+7.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+7.TIF" \* MERGEFORMATINET
(第18题)
19.(1)解:∵∠ACB=90°,AB=6 ,
BC=6,∴AC=12.∴AE=9.
∵AB∥CD,
∴△CDE∽△ABE.
∴=,
∴CD===2 .
(2)证明:∵∠ACB=90°,
CE=3,BC=6,∴BE=3 .
∵△CDE∽△ABE,
∴==,∴DE=,
∴BD=4 .
∵==,∠D=∠D,
∴△CDE∽△BDC.
20.(1)证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°.由折叠易得∠AFE=90°,
∴∠BAF+∠AFB=90°,
∠EFC+∠AFB=90°,
∴∠BAF=∠EFC,
∴△ABF∽△FCE.
(2)解:在矩形ABCD中,
易得BC=AD=AF=4.
在Rt△ABF中,BF==2,
∴CF=BC-BF=2.
∵△ABF∽△FCE,
∴=,即=.
解得CE=.
21.(1)证明:∵∠B=∠ADE=∠C,∴∠BAD=180°-∠ADB-∠ADE.
∵∠CDE=180°-∠ADB-∠ADE,
∴∠BAD=∠CDE,
∴△BDA∽△CED.
(2)解:由题易知,∠BAC=90°.当AD=AE时,∠ADE=∠AED.
∵∠ADE=∠B=45°,
∴∠AED=45°.∴∠DAE=90°.
∴点D与点B重合,不合题意,舍去;
当EA=ED时,∠EAD=∠EDA=∠B=45°.
∵∠BAC=90°,
∴∠BAD=∠EAD=45°,
∴AD平分∠BAC,
∴AD垂直平分BC,∴BD=3;
当DA=DE时,
∵∠EDA=∠C,∠DAE=∠CAD,
∴△ADE∽△ACD,
∴DA∶AC=DE∶DC,
∴AC=DC.
∵∠BAC=90°,∠B=45°,BC=6,
∴AC=3 .∴DC=3 .
∴BD=BC-DC=6-3 .
综上所述,当△ADE是等腰三角形时,BD的长为3或6-3 .
22.(1)证明:∵四边形EFGH是矩形,∴HG∥BC,∴△AHG∽△ABC.
(2)解:∵四边形EFGH是矩形,∴∠HED=∠EHN=90°.
∵AD⊥BC,
∴四边形HEDN是矩形,
∴ND=EH=x.
∵AD=3,∴AN=3-x.
∵△AHG∽△ABC,∴=.
∴=,∴HG=9-3x.
∵矩形EFGH的面积=HG·HE,
∴y=x(9-3x)=-3x2+9x(023.(1)解:∵F为CD的中点,
∴DF=CF.
∵四边形ABCD为正方形,
∴AD∥BC,AD=BC,
∴∠GDF=∠ECF=90°.
又∵∠DFG=∠CFE.
∴△GDF≌△ECF,
∴DG=CE.∵BC=3CE,
∴CE=BC=DG,
∴AG=AD-DG=BC-CE=BC-BC=BC,
∴==2.
(2)证明:过点G作GH⊥BC于点H,
易得CH=DG=CE=BC,
∴EH=CH+CE=BC.
在△ABG和△HGE中,∵AG=EH=BC,∠A=∠GHE=90°,AB=GH,∴△ABG≌△HGE,
∴BG=EG.
(3)证明:过点M作MT∥AD交BG于点T,
∵M为AB的中点,
∴MT=AG=DG.
∵AD∥MT,∴∠NMT=∠NDG.
在△MNT和△DNG中,
∵∠MNT=∠DNG,∠NMT=∠NDG,MT=DG,∴△MNT≌△DNG(AAS),
∴NT=NG.
∴BG=4NG,∴=.
∵BC=3CE,∴=,
∴=.
∵∠CBN=∠EBG,
∴△CBN∽△EBG,
∴∠BCN=∠BEG,∴CN∥EG.
PAGE
(限时: 120分钟 满分: 150分)
班级: 姓名: 得分:
一、选择题(本大题共10小题,每小题4分,共40分)
1.若2a-3b=0,则等于( )
A. B.- C. D.-
2.下列各组线段中,是成比例线段的一组是( )
A.a=4,b=6,c=5,d=10
B.a=2,b=4,c=3,d=6
C.a=2,b=,c=2 ,d=10
D.a=0.8,b=3,c=1,d=10
3.如图,在△ABC中,DE∥BC,AD=2,BD=3,AC=10,则AE的长为( )
A.3 B.4 C.5 D.6
INCLUDEPICTURE"卷+21.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+21.TIF" \* MERGEFORMATINET INCLUDEPICTURE"卷+22.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+22.TIF" \* MERGEFORMATINET INCLUDEPICTURE"卷+23.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+23.TIF" \* MERGEFORMATINET
(第3题) (第5题) (第6题)
4.已知线段AB=2,点P是线段AB的黄金分割点(AP>BP),则线段AP的长为( )
A.+1 B.-1
C. D.
5.如图,在△ABC中,点D、E分别在AB、AC边上,DE与BC不平行,那么下列条件中,不能判断△ADE∽△ACB的是( )
A.∠ADE=∠C B.∠AED=∠B
C.= D.=
6.如图,在△ABC中,AB∥DE,若=,则△ECD与△ACB的面积之比为( )
A. B. C. D.
7.如图,在△ABC中,D为AC边上一点,∠DBC=∠A,BC=,AC=3,则AD等于( )
A.2 B.1 C. D.
INCLUDEPICTURE"卷+16.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+16.TIF" \* MERGEFORMATINET INCLUDEPICTURE"卷+24.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+24.TIF" \* MERGEFORMATINET INCLUDEPICTURE"卷+25.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+25.TIF" \* MERGEFORMATINET
(第7题) (第8题) (第9题)
8.如图,在△ABC中,∠ACB=90°,AB=2,延长BC到点D,使BD=3CD,若E是AC的中点,则DE的长为( )
A. B. C. D.1
9.如图,△ABC中,CD⊥AB于D,①∠BCD=∠A;②AD∶AC=CD∶CB;③∠B+∠ACD=90°;④BC∶AC∶AB=3∶4∶5;⑤AC∶BD=AD∶CD.一定能确定△ABC为直角三角形的条件是( )
A.①②③ B.①②④
C.①②③④ D.③④⑤
10.如图,在△ACD中,AD=6,BC=5,AC2=AB(AB+BC),且△DAB∽△DCA,若AD=3AP,Q是线段AB上的动点,则PQ的最小值是( )
A. B. C. D.
INCLUDEPICTURE"卷+27.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+27.TIF" \* MERGEFORMATINET INCLUDEPICTURE"卷+28.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+28.TIF" \* MERGEFORMATINET
(第10题) (第12题)
二、填空题(本大题共4小题,每小题5分,共20分)
11.已知△ABC∽△A′B′C′,AD和A′D′是它们的对应中线,若AD=8,A′D′=6,则△ABC与△A′B′C′的周长比是________.
12.如图,在平面直角坐标系中,矩形OABC的顶点坐标分别是O(0,0),C(6,0),B(6,4),A(0,4),已知矩形OA′B′C′与矩形OABC位似,位似中心是原点O,且矩形OA′B′C′的面积等于矩形OABC面积的,则点B′的坐标是______________.
13.已知三角形纸片(△ABC)中,AB=AC=5,BC=8,将三角形按照如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是________.
INCLUDEPICTURE"卷+29.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+29.TIF" \* MERGEFORMATINET INCLUDEPICTURE"卷+30.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+30.TIF" \* MERGEFORMATINET
(第13题) (第14题)
14.如图,已知△ABC是等边三角形,点D,E,F分别是AB,AC,BC边上的点,∠EDF=120°,设=n.
(1)若n=1,则=________;
(2)若+=3,则n=________.
三、解答题(本大题共9小题,共90分)
15.(8分)已知:=.
(1)求的值;
(2)求的值.
16.(8分)如图,已知DE∥BC,FE∥CD,AF=3,AD=5,AE=4.
(1)求CE的长;
(2)求AB的长.
INCLUDEPICTURE"卷+31.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+31.TIF" \* MERGEFORMATINET
(第16题)
17.(8分)如图,在平面直角坐标系中,每个小正方形的边长都是1个单位,△ABC的顶点都在格点上.
(1)以原点O为位似中心,在第三象限内画出将△ABC放大为原来的2倍后的位似图形△A1B1C1;
(2)已知△ABC的面积为,则△A1B1C1的面积是______.
INCLUDEPICTURE"卷+32.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+32.TIF" \* MERGEFORMATINET
(第17题)
18.(8分)如图,在△ABC中,AD平分∠BAC.求证:=.
INCLUDEPICTURE"卷+33.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+33.TIF" \* MERGEFORMATINET
(第18题)
19.(10分)如图,AB∥CD,AC与BD交于点E,且∠ACB=90°,AB=6 ,BC=6,CE=3.
(1)求CD的长;
(2)求证:△CDE∽△BDC.
INCLUDEPICTURE"卷+34.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+34.TIF" \* MERGEFORMATINET
(第19题)
20.(10分)如图,在矩形ABCD中,E为DC上的一点,把△ADE沿AE翻折,使点D恰好落在BC边上的点F.
(1)求证:△ABF∽△FCE;
(2)若AB=2 ,AD=4,求CE的长.
INCLUDEPICTURE"卷+35.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+35.TIF" \* MERGEFORMATINET
(第20题)
21.(12分)如图,在△ABC中,点D、E分别在边BC、AC上,连接AD、DE,且∠B=∠ADE=∠C.
(1)求证:△BDA∽△CED;
(2)若∠B=45°,BC=6,当点D在BC上运动(点D不与B、C重合),且△ADE是等腰三角形时,求BD的长.
INCLUDEPICTURE"卷+36.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+36.TIF" \* MERGEFORMATINET
(第21题)
22.(12分)如图,矩形EFGH内接于△ABC(矩形各顶点在三角形边上),点E,F在BC上,点H,G分别在AB,AC上,且AD⊥BC于点D,交HG于点N.
(1)求证:△AHG∽△ABC;
(2)若AD=3,BC=9,设EH=x,矩形EFGH的面积为y,求出y与x之间的函数表达式,并写出自变量x的取值范围.
INCLUDEPICTURE"卷+37.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+37.TIF" \* MERGEFORMATINET
(第22题)
23.(14分)如图①,在正方形ABCD中,E为BC延长线上一点,且BC=3CE,F为CD的中点,EF的延长线交AD于点G,连接BG.
(1)求的值;
(2)求证:BG=EG;
(3)如图②,M为AB的中点,DM交BG于点N,连接CN,求证:CN∥GE.
INCLUDEPICTURE"卷+38.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+38.TIF" \* MERGEFORMATINET
(第23题)
答案
一、1.A 2.B 3.B 4.B 5.C
6.B 7.B 8.D 9.B
10.A 点拨:∵△DAB∽△DCA,
∴=,∴=.
解得BD=4(负值舍去).
∴===,
∴AC=AB.
∵AC2=AB(AB+BC),
∴=AB(AB+BC),解得AB=4,AB=0(舍去),
∴AB=BD=4.
过点B作BH⊥AD于点H,
∴AH=AD=3,
∴BH==.
∵AD=3AP,AD=6,∴AP=2.
当PQ⊥AB时,PQ的值最小,
∵∠AQP=∠AHB=90°,∠PAQ=∠BAH,
∴△APQ∽△ABH,
∴=,
∴=,∴PQ=.
二、11.4?3 12.(3,2)或(-3,-2)
13.
14.(1)1 (2)或
三、15.解:∵=,∴x=2y.
(1)==.
(2)==.
16.解:(1)∵FE∥CD,∴=.即=,解得AC=.
则CE=AC-AE=.
(2)∵DE∥BC,∴=.
即=,解得AB=.
17.解:(1)略 (2)14
18.证明:如图,过点B作BE∥AC,交线段AD的延长线于点E.
∵BE∥AC,∴△BDE∽△CDA.
∴∠BED=∠CAD,=.
∵AD平分∠BAC,
∴∠CAD=∠BAD,
∴∠BED=∠BAD.
∴AB=BE,∴=.
INCLUDEPICTURE"答卷+7.TIF" INCLUDEPICTURE "D:\\方正转Word\\9数HK安徽\\答卷+7.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+7.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+7.TIF" \* MERGEFORMATINET
(第18题)
19.(1)解:∵∠ACB=90°,AB=6 ,
BC=6,∴AC=12.∴AE=9.
∵AB∥CD,
∴△CDE∽△ABE.
∴=,
∴CD===2 .
(2)证明:∵∠ACB=90°,
CE=3,BC=6,∴BE=3 .
∵△CDE∽△ABE,
∴==,∴DE=,
∴BD=4 .
∵==,∠D=∠D,
∴△CDE∽△BDC.
20.(1)证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°.由折叠易得∠AFE=90°,
∴∠BAF+∠AFB=90°,
∠EFC+∠AFB=90°,
∴∠BAF=∠EFC,
∴△ABF∽△FCE.
(2)解:在矩形ABCD中,
易得BC=AD=AF=4.
在Rt△ABF中,BF==2,
∴CF=BC-BF=2.
∵△ABF∽△FCE,
∴=,即=.
解得CE=.
21.(1)证明:∵∠B=∠ADE=∠C,∴∠BAD=180°-∠ADB-∠ADE.
∵∠CDE=180°-∠ADB-∠ADE,
∴∠BAD=∠CDE,
∴△BDA∽△CED.
(2)解:由题易知,∠BAC=90°.当AD=AE时,∠ADE=∠AED.
∵∠ADE=∠B=45°,
∴∠AED=45°.∴∠DAE=90°.
∴点D与点B重合,不合题意,舍去;
当EA=ED时,∠EAD=∠EDA=∠B=45°.
∵∠BAC=90°,
∴∠BAD=∠EAD=45°,
∴AD平分∠BAC,
∴AD垂直平分BC,∴BD=3;
当DA=DE时,
∵∠EDA=∠C,∠DAE=∠CAD,
∴△ADE∽△ACD,
∴DA∶AC=DE∶DC,
∴AC=DC.
∵∠BAC=90°,∠B=45°,BC=6,
∴AC=3 .∴DC=3 .
∴BD=BC-DC=6-3 .
综上所述,当△ADE是等腰三角形时,BD的长为3或6-3 .
22.(1)证明:∵四边形EFGH是矩形,∴HG∥BC,∴△AHG∽△ABC.
(2)解:∵四边形EFGH是矩形,∴∠HED=∠EHN=90°.
∵AD⊥BC,
∴四边形HEDN是矩形,
∴ND=EH=x.
∵AD=3,∴AN=3-x.
∵△AHG∽△ABC,∴=.
∴=,∴HG=9-3x.
∵矩形EFGH的面积=HG·HE,
∴y=x(9-3x)=-3x2+9x(0
∴DF=CF.
∵四边形ABCD为正方形,
∴AD∥BC,AD=BC,
∴∠GDF=∠ECF=90°.
又∵∠DFG=∠CFE.
∴△GDF≌△ECF,
∴DG=CE.∵BC=3CE,
∴CE=BC=DG,
∴AG=AD-DG=BC-CE=BC-BC=BC,
∴==2.
(2)证明:过点G作GH⊥BC于点H,
易得CH=DG=CE=BC,
∴EH=CH+CE=BC.
在△ABG和△HGE中,∵AG=EH=BC,∠A=∠GHE=90°,AB=GH,∴△ABG≌△HGE,
∴BG=EG.
(3)证明:过点M作MT∥AD交BG于点T,
∵M为AB的中点,
∴MT=AG=DG.
∵AD∥MT,∴∠NMT=∠NDG.
在△MNT和△DNG中,
∵∠MNT=∠DNG,∠NMT=∠NDG,MT=DG,∴△MNT≌△DNG(AAS),
∴NT=NG.
∴BG=4NG,∴=.
∵BC=3CE,∴=,
∴=.
∵∠CBN=∠EBG,
∴△CBN∽△EBG,
∴∠BCN=∠BEG,∴CN∥EG.
PAGE
