沪科版九年级数学上册 名校 期末达标检测卷(word版含答案)
文档属性
| 名称 | 沪科版九年级数学上册 名校 期末达标检测卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 335.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 14:17:18 | ||
图片预览



文档简介
沪科版九年级数学上册 名校期末达标检测卷
(限时: 120分钟 满分: 150分)
班级: 姓名: 得分:
一、选择题(本大题共10小题,每小题4分,共40分)
1.cos 30°的值是( )
A. B. C. D.
2.下列函数中,是二次函数的是( )
A.y=-2x-1 B.y=2x2
C.y= D.y=ax2+bx+c
3.在平面直角坐标系中,将二次函数y=x2的图象向左平移2个单位,再向上平移1个单位所得抛物线对应的函数表达式为( )
A.y=(x-2)2+1 B.y=(x+2)2+1
C.y=(x+2)2-1 D.y=(x-2)2-1
4.在Rt△ABC中,∠C=90°,若AB=2AC,则cos A的值等于( )
A. B. C. D.
5.已知反比例函数y=-的图象上有两点A(x1,y1),B(x2,y2),且x1<x2<0,则y1,y2的大小关系为( )
A.y1<y2 B.y1>y2
C.y1=y2 D.无法确定
6.如图,已知DE∥BC,CD和BE相交于点O,S△DOE?S△COB=9?16,则DE?BC为( )
INCLUDEPICTURE"卷+58.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+58.TIF" \* MERGEFORMATINET
(第6题)
A.2∶3
B.3∶4
C.9∶16
D.1∶2
7.下表中列出了二次函数y=ax2+bx+c(a≠0)的一些对应值,则一元二次方程ax2+bx+c=0(a≠0)的一个近似解x1的范围是( )
x … -3 -2 -1 0 1 …
y … -11 -5 -1 1 1 …
A.-3<x1<-2 B.-2<x1<-1
C.-1<x1<0 D.0<x1<1
8.二次函数y=ax2+bx-2(a≠0)的图象的顶点在第三象限,且过点(1,0),设t=a-b-2,则t的变化范围是( )
A.-2<t<0 B.-3<t<0
C.-4<t<-2 D.-4<t<0
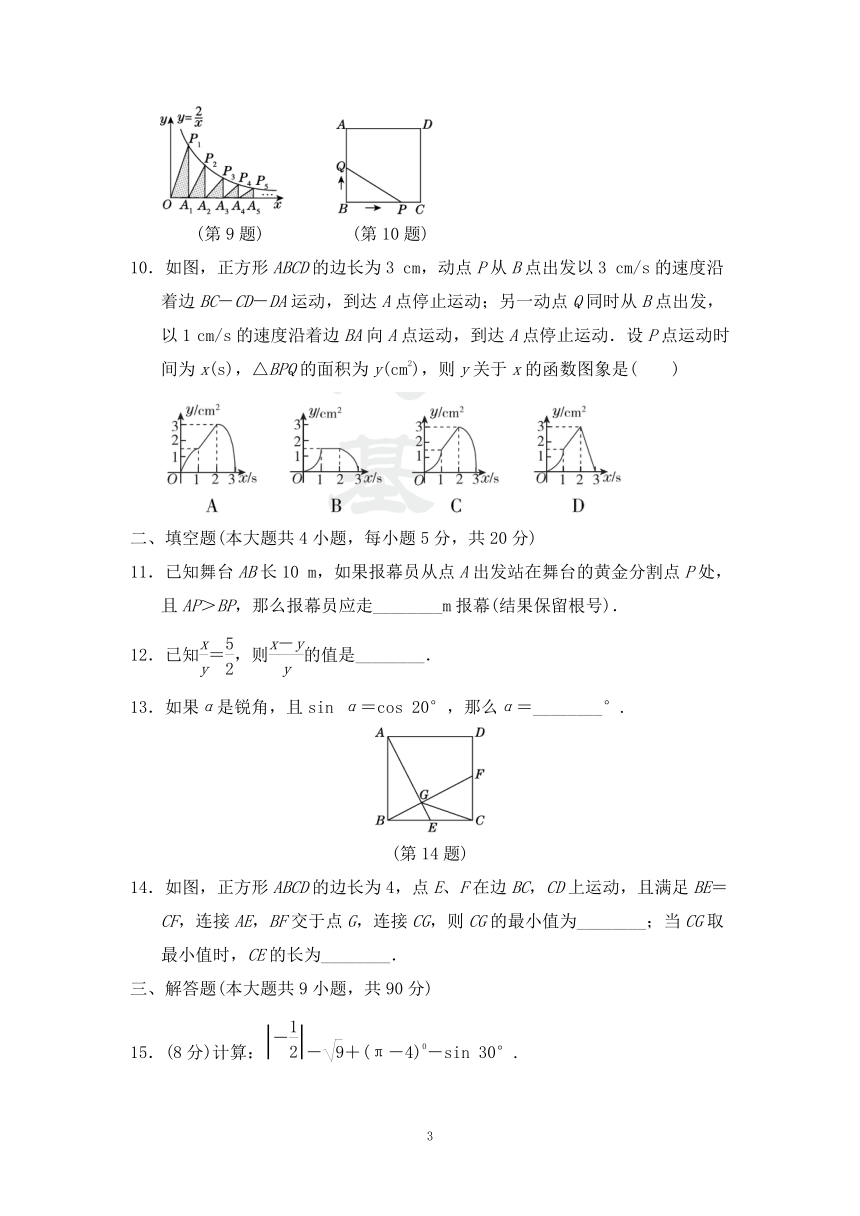
9.如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=…=A2 021A2 022,过点A1、A2、A3、…、A2 021、A2 022分别作x轴的垂线,与反比例函数y=(x≠0)的图象相交于点P1、P2、P3、…、P2 021、P2 022,得直角三角形OP1A1、A1P2A2、A2P3A3、…、A2 021P2 022A2 022,并设其面积分别为S1、S2、S3、…、S2 021、S2 022,则S2 022的值为( )
A. B. C. D.
INCLUDEPICTURE"卷+59.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+59.TIF" \* MERGEFORMATINET INCLUDEPICTURE"卷+60.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+60.TIF" \* MERGEFORMATINET
(第9题) (第10题)
10.如图,正方形ABCD的边长为3 cm,动点P从B点出发以3 cm/s的速度沿着边BC-CD-DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1 cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
二、填空题(本大题共4小题,每小题5分,共20分)
11.已知舞台AB长10 m,如果报幕员从点A出发站在舞台的黄金分割点P处,且AP>BP,那么报幕员应走________m报幕(结果保留根号).
12.已知=,则的值是________.
13.如果α是锐角,且sin α=cos 20°,那么α=________°.
INCLUDEPICTURE"卷+65.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+65.TIF" \* MERGEFORMATINET
(第14题)
14.如图,正方形ABCD的边长为4,点E、F在边BC,CD上运动,且满足BE=CF,连接AE,BF交于点G,连接CG,则CG的最小值为________;当CG取最小值时,CE的长为________.
三、解答题(本大题共9小题,共90分)
15.(8分)计算:-+(π-4)0-sin 30°.
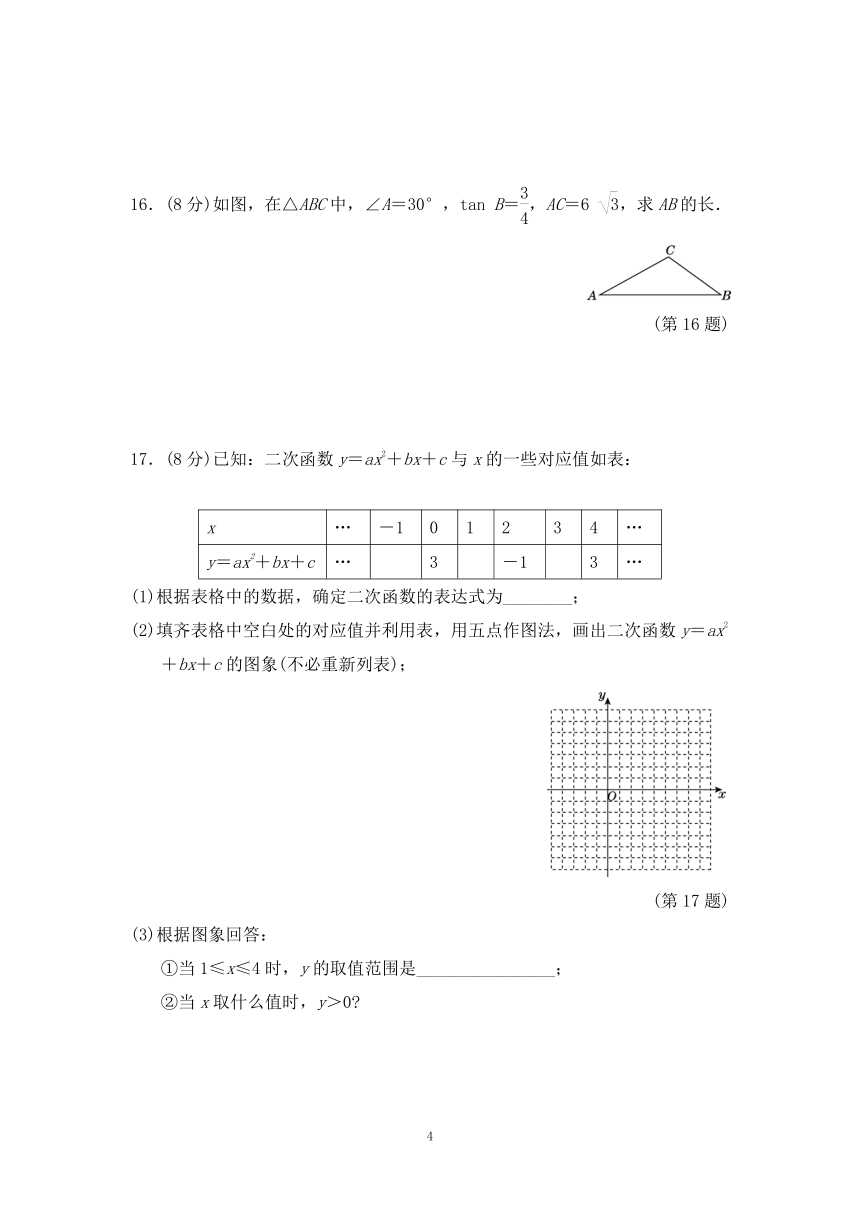
16.(8分)如图,在△ABC中,∠A=30°,tan B=,AC=6 ,求AB的长.
INCLUDEPICTURE"卷+66.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+66.TIF" \* MERGEFORMATINET
(第16题)
17.(8分)已知:二次函数y=ax2+bx+c与x的一些对应值如表:
x … -1 0 1 2 3 4 …
y=ax2+bx+c … 3 -1 3 …
(1)根据表格中的数据,确定二次函数的表达式为________;
(2)填齐表格中空白处的对应值并利用表,用五点作图法,画出二次函数y=ax2+bx+c的图象(不必重新列表);
INCLUDEPICTURE"卷+67.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+67.TIF" \* MERGEFORMATINET
(第17题)
(3)根据图象回答:
①当1≤x≤4时,y的取值范围是________________;
②当x取什么值时,y>0
18.(8分)如图,在12×12的正方形网格中,△CAB 的顶点坐标分别为C(1,1)、A(2,3)、B(4,2).
(1)以点C(1,1)为位似中心,按2?1的位似比在位似中心的同侧将△CAB放大为△CA′B′,放大后点A、B的对应点分别为A′、B′.画出△CA′B′,并写出点A′、B′的坐标;
INCLUDEPICTURE"卷+68.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+68.TIF" \* MERGEFORMATINET
(第18题)
(2)在(1)中,若P(a,b)为线段AB上任一点,请直接写出变化后点P的对应点P′的坐标.
19.(10分)已知:如图,△ABD∽△ACE.求证:
(1)∠DAE=∠BAC;
(2)△DAE∽△BAC.
INCLUDEPICTURE"卷+69.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+69.TIF" \* MERGEFORMATINET
(第19题)
20.(10分)如图,一次函数y=kx+b的图象与反比例函数y= 的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D.
(1)求反比例函数y=和一次函数y=kx+b的表达式;
(2)连接OA,OC.求△AOC的面积.
INCLUDEPICTURE"卷+70.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+70.TIF" \* MERGEFORMATINET
(第20题)
21.(12分)“山地自行车速降赛”是一种新兴的极限运动.深受青年人的喜爱,赛道需全部是下坡骑行路段.如图是某一下坡赛道,由AB,BC,CD三段组成,在同一平面内,其中AB段的俯角是30°,长为2 m,BC段与AB、CD段都垂直,长为1 m,CD段长为3 m,求此下坡路段的垂直高度.(结果保留根号)
INCLUDEPICTURE"卷+71.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+71.TIF" \* MERGEFORMATINET
(第21题)
22.(12分)某电子科技公司开发一种新产品,公司对经营的盈亏情况每月最后一天结算1次.在1~12月份中,公司前x个月累计获得的总利润y(万元)与销售时间x(月)之间满足二次函数表达式y=a(x-h)2+k,二次函数y=a(x-h)2+k的一部分图象如图所示,点A为抛物线的顶点,且点A、B、C的横坐标分别为4、10、12,点A、B的纵坐标分别为-16、20.
(1)试确定函数表达式y=a(x-h)2+k;
(2)分别求出前9个月公司累计获得的利润以及10月份一个月内所获得的利润;
(3)在1~12月份中,哪个月该公司一个月内所获得的利润最多?最多利润是多少万元?
INCLUDEPICTURE"卷+72.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+72.TIF" \* MERGEFORMATINET
(第22题)
23.(14分)在△ABC中,点P为边BC上一点,∠APD=∠B,PD交边AC于点D.
(1)如图①,若△ABC为等边三角形,求证:=;
(2)如图②,若∠APD=45°,且∠PAD=90°,AB=2,CD=,求△APC的面积.
INCLUDEPICTURE"卷+73.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+73.TIF" \* MERGEFORMATINET
(第23题)
答案
一、1.C 2.B 3.B 4.C 5.A
6.B 7.C 8.C 9.A
10.C 点拨:由题意可得BQ=x cm.
①当0≤x≤1时,点P在BC边上,BP=3x cm,
则△BPQ的面积=BP·BQ,
得y=·3x·x=x2;故A选项错误;
②当1则△BPQ的面积=BQ·BC,得y=·x·3=x;故B选项错误;
③当2则S△BPQ=AP·BQ,得y=·(9-3x)·x=x-x2;故D选项错误.故选C.
二、11.(5 -5) 12. 13.70
14.2 -2;6-2
点拨:如图①,取AB的中点H,连接HG,HC,
在△ABE和△BCF中,
∴△ABE≌△BCF(SAS),
∴∠BAE=∠CBF,
∴∠BAE+∠ABG=∠CBF+∠ABG=90°,
∴∠AGB=90°,
∴HG=AB=2,
∵HG、HC不变,∴当点H、G、C在同一条直线上时,CG取最小值,
∵HC==2,CG的最小值为HC-HG=2-2,当CG取最小值时,H、G、C共线,如图②,过点G作GK⊥AB于点K,
INCLUDEPICTURE"答卷+20.TIF" INCLUDEPICTURE "D:\\方正转Word\\9数HK安徽\\答卷+20.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+20.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+20.TIF" \* MERGEFORMATINET INCLUDEPICTURE"答卷+21.TIF" INCLUDEPICTURE "D:\\方正转Word\\9数HK安徽\\答卷+21.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+21.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+21.TIF" \* MERGEFORMATINET
(第14题)
∵∠GKH=∠CBH=90°,
∴GK∥BC,∴∠HCB=∠HGK,
∴tan∠HCB=tan∠HGK===.设HK=x,KG=2x,
∴HG==x,
∴HG=AH=x,
∴AK=AH+HK=(+1)x,
∴tan∠KAG=tan∠BAE====,
∴BE=×4=2(-1),
∴CE=4-BE=6-2 .
三、15.解:原式=-3+1-=-2.
16.解:过点C作CD⊥AB于点D.在Rt△CDA中,∠A=30°,
∴CD=AC·sin 30°=3 ,
AD=AC×cos 30°=9,
在Rt△CDB中,∵tan B=,
∴=,∴BD=4 ,
∴AB=AD+DB=9+4 .
17.解:(1)y=x2-4x+3
(2)如下表所示:
x … -1 0 1 2 3 4 …
y=ax2+bx+c … 8 3 0 -1 0 3 …
函数图象如图所示:
INCLUDEPICTURE"答卷+23.TIF" INCLUDEPICTURE "D:\\方正转Word\\9数HK安徽\\答卷+23.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+23.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+23.TIF" \* MERGEFORMATINET
(第17题)
(3)①-1≤y≤3
②当x<1或x>3时,y>0.
18.解:(1)如图,△CA′B′即为所求,其中A′(3,5),B′(7,3);
(2)P′(2a-1,2b-1).
INCLUDEPICTURE"答卷+24.TIF" INCLUDEPICTURE "D:\\方正转Word\\9数HK安徽\\答卷+24.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+24.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+24.TIF" \* MERGEFORMATINET
(第18题)
19.证明:(1)∵△ABD∽△ACE.
∴∠BAD=∠CAE,
∵∠BAD+∠BAE=∠BAE+∠CAE,∴∠DAE=∠BAC;
(2)∵△ABD∽△ACE,
∴=,∴=,
而∠DAE=∠BAC,
∴△DAE∽△BAC.
20.解:(1)把点A(-2,-5)的坐标代入y=,得-5=,解得m=10,则反比例函数的表达式是y=,把x=5代入,得y==2,则点C的坐标是(5,2).
根据题意得解得
则一次函数的表达式是y=x-3.
(2)在y=x-3中,令x=0,解得y=-3.则B的坐标是(0,-3).
所以OB=3.因为点A的横坐标是-2,点C的横坐标是5.所以S△AOC=S△AOB+S△BOC=OB×2+×OB×5=×3×7=.
21.解:如图,延长AB与直线l2交于点E,过D作DF⊥BE,过A作AG⊥DE,易得FD=BC=1 m,
BF=CD=3 m,∠FED=30°,
在Rt△DEF中,=tan30°,
即EF=m,∴AE=AB+BF+FE=(2+3+)m=(5+)m,在Rt△AGE中,AG=AE= m,则此下坡路段的垂直高度为 m.
INCLUDEPICTURE"答卷+25.TIF" INCLUDEPICTURE "D:\\方正转Word\\9数HK安徽\\答卷+25.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+25.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+25.TIF" \* MERGEFORMATINET
(第21题)
22.解:(1)根据题意可得y=a(x-4)2-16,当x=10时,y=20,所以a(10-4)2-16=20,解得a=1,所以函数表达式为y=(x-4)2-16.
(2)当x=9时,y=(9-4)2-16=9,所以前9个月公司累计获得的利润为9万元,又由题意可知,当x=10时,y=20,而20-9=11(万元),所以10月份一个月内所获得的利润为11万元.
(3)设在1~12月份中,第n个月该公司一个月内所获得的利润为s万元,则有:s=(n-4)2-16-[(n-1-4)2-16]=2n-9,因为s是关于n的一次函数,且2>0,所以s随n的增大而增大,而n的最大值为12,所以当n=12时,s=15,所以12月份该公司一个月内所获得的利润最多,最多利润是15万元.
23.(1)证明:在△ABP中,∠B+∠BAP+∠APB=180°,
∵∠APD=∠B=∠C,
∴∠APD+∠BAP+∠APB=180°,
∵∠APB+∠APD+∠CPD=180°,
∴∠BAP=∠CPD,
∴△ABP∽△PCD,∴=.
(2)解:如图,过点D作∠DNP=45°,在△ABP中,∠B+∠BAP+∠APB=180°,∵∠B=∠APD,
∴∠APD+∠BAP+∠APB=180°,
∵∠APB+∠APD+∠DPN=180°,
∴∠BAP=∠DPN.
又由题意易得∠B=∠PND,
∴△ABP∽△PND.
∵∠APD=45°,∠PAD=90°,
∴∠ADP=90°-∠APD=45°,
∴AP=AD,∴△APD为等腰直角三角形,∴==,
∴PN=4.由△ABP∽△PND,得∠APB=∠PDN,
∴∠DPC+∠APD=∠CDN+∠ADP,∴∠DPC=∠CDN.
又∠C=∠C,∴△CDN∽△CPD,
∴=,即=,
∴CN=1,∴PC=1+4=5,在Rt△APC中,由勾股定理可得AP=,∴AD=,
∴AC=AD+CD=2 ,
∴S△APC=×AP×AC=××2=5.
INCLUDEPICTURE"答卷+26.TIF" INCLUDEPICTURE "D:\\方正转Word\\9数HK安徽\\答卷+26.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+26.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+26.TIF" \* MERGEFORMATINET
(第23题)
PAGE
(限时: 120分钟 满分: 150分)
班级: 姓名: 得分:
一、选择题(本大题共10小题,每小题4分,共40分)
1.cos 30°的值是( )
A. B. C. D.
2.下列函数中,是二次函数的是( )
A.y=-2x-1 B.y=2x2
C.y= D.y=ax2+bx+c
3.在平面直角坐标系中,将二次函数y=x2的图象向左平移2个单位,再向上平移1个单位所得抛物线对应的函数表达式为( )
A.y=(x-2)2+1 B.y=(x+2)2+1
C.y=(x+2)2-1 D.y=(x-2)2-1
4.在Rt△ABC中,∠C=90°,若AB=2AC,则cos A的值等于( )
A. B. C. D.
5.已知反比例函数y=-的图象上有两点A(x1,y1),B(x2,y2),且x1<x2<0,则y1,y2的大小关系为( )
A.y1<y2 B.y1>y2
C.y1=y2 D.无法确定
6.如图,已知DE∥BC,CD和BE相交于点O,S△DOE?S△COB=9?16,则DE?BC为( )
INCLUDEPICTURE"卷+58.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+58.TIF" \* MERGEFORMATINET
(第6题)
A.2∶3
B.3∶4
C.9∶16
D.1∶2
7.下表中列出了二次函数y=ax2+bx+c(a≠0)的一些对应值,则一元二次方程ax2+bx+c=0(a≠0)的一个近似解x1的范围是( )
x … -3 -2 -1 0 1 …
y … -11 -5 -1 1 1 …
A.-3<x1<-2 B.-2<x1<-1
C.-1<x1<0 D.0<x1<1
8.二次函数y=ax2+bx-2(a≠0)的图象的顶点在第三象限,且过点(1,0),设t=a-b-2,则t的变化范围是( )
A.-2<t<0 B.-3<t<0
C.-4<t<-2 D.-4<t<0
9.如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=…=A2 021A2 022,过点A1、A2、A3、…、A2 021、A2 022分别作x轴的垂线,与反比例函数y=(x≠0)的图象相交于点P1、P2、P3、…、P2 021、P2 022,得直角三角形OP1A1、A1P2A2、A2P3A3、…、A2 021P2 022A2 022,并设其面积分别为S1、S2、S3、…、S2 021、S2 022,则S2 022的值为( )
A. B. C. D.
INCLUDEPICTURE"卷+59.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+59.TIF" \* MERGEFORMATINET INCLUDEPICTURE"卷+60.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+60.TIF" \* MERGEFORMATINET
(第9题) (第10题)
10.如图,正方形ABCD的边长为3 cm,动点P从B点出发以3 cm/s的速度沿着边BC-CD-DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1 cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
二、填空题(本大题共4小题,每小题5分,共20分)
11.已知舞台AB长10 m,如果报幕员从点A出发站在舞台的黄金分割点P处,且AP>BP,那么报幕员应走________m报幕(结果保留根号).
12.已知=,则的值是________.
13.如果α是锐角,且sin α=cos 20°,那么α=________°.
INCLUDEPICTURE"卷+65.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+65.TIF" \* MERGEFORMATINET
(第14题)
14.如图,正方形ABCD的边长为4,点E、F在边BC,CD上运动,且满足BE=CF,连接AE,BF交于点G,连接CG,则CG的最小值为________;当CG取最小值时,CE的长为________.
三、解答题(本大题共9小题,共90分)
15.(8分)计算:-+(π-4)0-sin 30°.
16.(8分)如图,在△ABC中,∠A=30°,tan B=,AC=6 ,求AB的长.
INCLUDEPICTURE"卷+66.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+66.TIF" \* MERGEFORMATINET
(第16题)
17.(8分)已知:二次函数y=ax2+bx+c与x的一些对应值如表:
x … -1 0 1 2 3 4 …
y=ax2+bx+c … 3 -1 3 …
(1)根据表格中的数据,确定二次函数的表达式为________;
(2)填齐表格中空白处的对应值并利用表,用五点作图法,画出二次函数y=ax2+bx+c的图象(不必重新列表);
INCLUDEPICTURE"卷+67.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+67.TIF" \* MERGEFORMATINET
(第17题)
(3)根据图象回答:
①当1≤x≤4时,y的取值范围是________________;
②当x取什么值时,y>0
18.(8分)如图,在12×12的正方形网格中,△CAB 的顶点坐标分别为C(1,1)、A(2,3)、B(4,2).
(1)以点C(1,1)为位似中心,按2?1的位似比在位似中心的同侧将△CAB放大为△CA′B′,放大后点A、B的对应点分别为A′、B′.画出△CA′B′,并写出点A′、B′的坐标;
INCLUDEPICTURE"卷+68.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+68.TIF" \* MERGEFORMATINET
(第18题)
(2)在(1)中,若P(a,b)为线段AB上任一点,请直接写出变化后点P的对应点P′的坐标.
19.(10分)已知:如图,△ABD∽△ACE.求证:
(1)∠DAE=∠BAC;
(2)△DAE∽△BAC.
INCLUDEPICTURE"卷+69.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+69.TIF" \* MERGEFORMATINET
(第19题)
20.(10分)如图,一次函数y=kx+b的图象与反比例函数y= 的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D.
(1)求反比例函数y=和一次函数y=kx+b的表达式;
(2)连接OA,OC.求△AOC的面积.
INCLUDEPICTURE"卷+70.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+70.TIF" \* MERGEFORMATINET
(第20题)
21.(12分)“山地自行车速降赛”是一种新兴的极限运动.深受青年人的喜爱,赛道需全部是下坡骑行路段.如图是某一下坡赛道,由AB,BC,CD三段组成,在同一平面内,其中AB段的俯角是30°,长为2 m,BC段与AB、CD段都垂直,长为1 m,CD段长为3 m,求此下坡路段的垂直高度.(结果保留根号)
INCLUDEPICTURE"卷+71.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+71.TIF" \* MERGEFORMATINET
(第21题)
22.(12分)某电子科技公司开发一种新产品,公司对经营的盈亏情况每月最后一天结算1次.在1~12月份中,公司前x个月累计获得的总利润y(万元)与销售时间x(月)之间满足二次函数表达式y=a(x-h)2+k,二次函数y=a(x-h)2+k的一部分图象如图所示,点A为抛物线的顶点,且点A、B、C的横坐标分别为4、10、12,点A、B的纵坐标分别为-16、20.
(1)试确定函数表达式y=a(x-h)2+k;
(2)分别求出前9个月公司累计获得的利润以及10月份一个月内所获得的利润;
(3)在1~12月份中,哪个月该公司一个月内所获得的利润最多?最多利润是多少万元?
INCLUDEPICTURE"卷+72.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+72.TIF" \* MERGEFORMATINET
(第22题)
23.(14分)在△ABC中,点P为边BC上一点,∠APD=∠B,PD交边AC于点D.
(1)如图①,若△ABC为等边三角形,求证:=;
(2)如图②,若∠APD=45°,且∠PAD=90°,AB=2,CD=,求△APC的面积.
INCLUDEPICTURE"卷+73.TIF" INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\卷+73.TIF" \* MERGEFORMATINET
(第23题)
答案
一、1.C 2.B 3.B 4.C 5.A
6.B 7.C 8.C 9.A
10.C 点拨:由题意可得BQ=x cm.
①当0≤x≤1时,点P在BC边上,BP=3x cm,
则△BPQ的面积=BP·BQ,
得y=·3x·x=x2;故A选项错误;
②当1
③当2
二、11.(5 -5) 12. 13.70
14.2 -2;6-2
点拨:如图①,取AB的中点H,连接HG,HC,
在△ABE和△BCF中,
∴△ABE≌△BCF(SAS),
∴∠BAE=∠CBF,
∴∠BAE+∠ABG=∠CBF+∠ABG=90°,
∴∠AGB=90°,
∴HG=AB=2,
∵HG、HC不变,∴当点H、G、C在同一条直线上时,CG取最小值,
∵HC==2,CG的最小值为HC-HG=2-2,当CG取最小值时,H、G、C共线,如图②,过点G作GK⊥AB于点K,
INCLUDEPICTURE"答卷+20.TIF" INCLUDEPICTURE "D:\\方正转Word\\9数HK安徽\\答卷+20.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+20.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+20.TIF" \* MERGEFORMATINET INCLUDEPICTURE"答卷+21.TIF" INCLUDEPICTURE "D:\\方正转Word\\9数HK安徽\\答卷+21.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+21.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+21.TIF" \* MERGEFORMATINET
(第14题)
∵∠GKH=∠CBH=90°,
∴GK∥BC,∴∠HCB=∠HGK,
∴tan∠HCB=tan∠HGK===.设HK=x,KG=2x,
∴HG==x,
∴HG=AH=x,
∴AK=AH+HK=(+1)x,
∴tan∠KAG=tan∠BAE====,
∴BE=×4=2(-1),
∴CE=4-BE=6-2 .
三、15.解:原式=-3+1-=-2.
16.解:过点C作CD⊥AB于点D.在Rt△CDA中,∠A=30°,
∴CD=AC·sin 30°=3 ,
AD=AC×cos 30°=9,
在Rt△CDB中,∵tan B=,
∴=,∴BD=4 ,
∴AB=AD+DB=9+4 .
17.解:(1)y=x2-4x+3
(2)如下表所示:
x … -1 0 1 2 3 4 …
y=ax2+bx+c … 8 3 0 -1 0 3 …
函数图象如图所示:
INCLUDEPICTURE"答卷+23.TIF" INCLUDEPICTURE "D:\\方正转Word\\9数HK安徽\\答卷+23.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+23.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+23.TIF" \* MERGEFORMATINET
(第17题)
(3)①-1≤y≤3
②当x<1或x>3时,y>0.
18.解:(1)如图,△CA′B′即为所求,其中A′(3,5),B′(7,3);
(2)P′(2a-1,2b-1).
INCLUDEPICTURE"答卷+24.TIF" INCLUDEPICTURE "D:\\方正转Word\\9数HK安徽\\答卷+24.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+24.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+24.TIF" \* MERGEFORMATINET
(第18题)
19.证明:(1)∵△ABD∽△ACE.
∴∠BAD=∠CAE,
∵∠BAD+∠BAE=∠BAE+∠CAE,∴∠DAE=∠BAC;
(2)∵△ABD∽△ACE,
∴=,∴=,
而∠DAE=∠BAC,
∴△DAE∽△BAC.
20.解:(1)把点A(-2,-5)的坐标代入y=,得-5=,解得m=10,则反比例函数的表达式是y=,把x=5代入,得y==2,则点C的坐标是(5,2).
根据题意得解得
则一次函数的表达式是y=x-3.
(2)在y=x-3中,令x=0,解得y=-3.则B的坐标是(0,-3).
所以OB=3.因为点A的横坐标是-2,点C的横坐标是5.所以S△AOC=S△AOB+S△BOC=OB×2+×OB×5=×3×7=.
21.解:如图,延长AB与直线l2交于点E,过D作DF⊥BE,过A作AG⊥DE,易得FD=BC=1 m,
BF=CD=3 m,∠FED=30°,
在Rt△DEF中,=tan30°,
即EF=m,∴AE=AB+BF+FE=(2+3+)m=(5+)m,在Rt△AGE中,AG=AE= m,则此下坡路段的垂直高度为 m.
INCLUDEPICTURE"答卷+25.TIF" INCLUDEPICTURE "D:\\方正转Word\\9数HK安徽\\答卷+25.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+25.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+25.TIF" \* MERGEFORMATINET
(第21题)
22.解:(1)根据题意可得y=a(x-4)2-16,当x=10时,y=20,所以a(10-4)2-16=20,解得a=1,所以函数表达式为y=(x-4)2-16.
(2)当x=9时,y=(9-4)2-16=9,所以前9个月公司累计获得的利润为9万元,又由题意可知,当x=10时,y=20,而20-9=11(万元),所以10月份一个月内所获得的利润为11万元.
(3)设在1~12月份中,第n个月该公司一个月内所获得的利润为s万元,则有:s=(n-4)2-16-[(n-1-4)2-16]=2n-9,因为s是关于n的一次函数,且2>0,所以s随n的增大而增大,而n的最大值为12,所以当n=12时,s=15,所以12月份该公司一个月内所获得的利润最多,最多利润是15万元.
23.(1)证明:在△ABP中,∠B+∠BAP+∠APB=180°,
∵∠APD=∠B=∠C,
∴∠APD+∠BAP+∠APB=180°,
∵∠APB+∠APD+∠CPD=180°,
∴∠BAP=∠CPD,
∴△ABP∽△PCD,∴=.
(2)解:如图,过点D作∠DNP=45°,在△ABP中,∠B+∠BAP+∠APB=180°,∵∠B=∠APD,
∴∠APD+∠BAP+∠APB=180°,
∵∠APB+∠APD+∠DPN=180°,
∴∠BAP=∠DPN.
又由题意易得∠B=∠PND,
∴△ABP∽△PND.
∵∠APD=45°,∠PAD=90°,
∴∠ADP=90°-∠APD=45°,
∴AP=AD,∴△APD为等腰直角三角形,∴==,
∴PN=4.由△ABP∽△PND,得∠APB=∠PDN,
∴∠DPC+∠APD=∠CDN+∠ADP,∴∠DPC=∠CDN.
又∠C=∠C,∴△CDN∽△CPD,
∴=,即=,
∴CN=1,∴PC=1+4=5,在Rt△APC中,由勾股定理可得AP=,∴AD=,
∴AC=AD+CD=2 ,
∴S△APC=×AP×AC=××2=5.
INCLUDEPICTURE"答卷+26.TIF" INCLUDEPICTURE "D:\\方正转Word\\9数HK安徽\\答卷+26.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+26.TIF" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数HK安徽\\文件\\答卷+26.TIF" \* MERGEFORMATINET
(第23题)
PAGE
同课章节目录
