冀教版5年级下册课程实录_5.4.3倒数
文档属性
| 名称 | 冀教版5年级下册课程实录_5.4.3倒数 |

|
|
| 格式 | docx | ||
| 文件大小 | 57.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 09:14:02 | ||
图片预览

文档简介
冀教版五下四单元三小节 倒数
旁白:课间的时候,糖糖去找可可玩,发现可可眉头紧锁,一脸的疑惑,她赶紧去询问原因,想帮可可解决麻烦,等可可说了自己的问题后她也是一筹莫展,最后他们决定一起去找小慧老师帮忙。
可可:老师您好,我们遇到了一点麻烦,想请您指导一下我们。
小慧老师:我们的“小诸葛”也有麻烦了,说出来我们一起解决。
可可:我在做练习的时候,遇到了这样一组算式:(配音要读以下算式)
×=1 2×=1 ×=1
×10=1 ×=1 7×=1
我发现它们的结果都是1,感觉很奇怪,但是又总结不出其中的规律。
(女)小慧老师:除了结果都是1之外,这些算式还有哪些相同的特点呢?
(女)糖糖:我看出来了,我把以上算式中的整数看成分母是1的分数。发现每个算式中两个乘数的分子、分母交换了位置。
(女)糖糖:所以这六道算式有两个特点①两个数的乘积都是1。②两个乘数的分子,分母相互颠倒(dao第三声)。
(女)小慧老师:糖糖总结的很好,通常我们称乘积为1的两个数互为倒(dao第四声)数。
(女)小慧老师:倒数是指两个数字之间相互依存的一种关系。必须说,一个数是另一个数的倒数。不能孤立的说,某一个数是倒数。这是一个新的概念,你们还没有接触到。
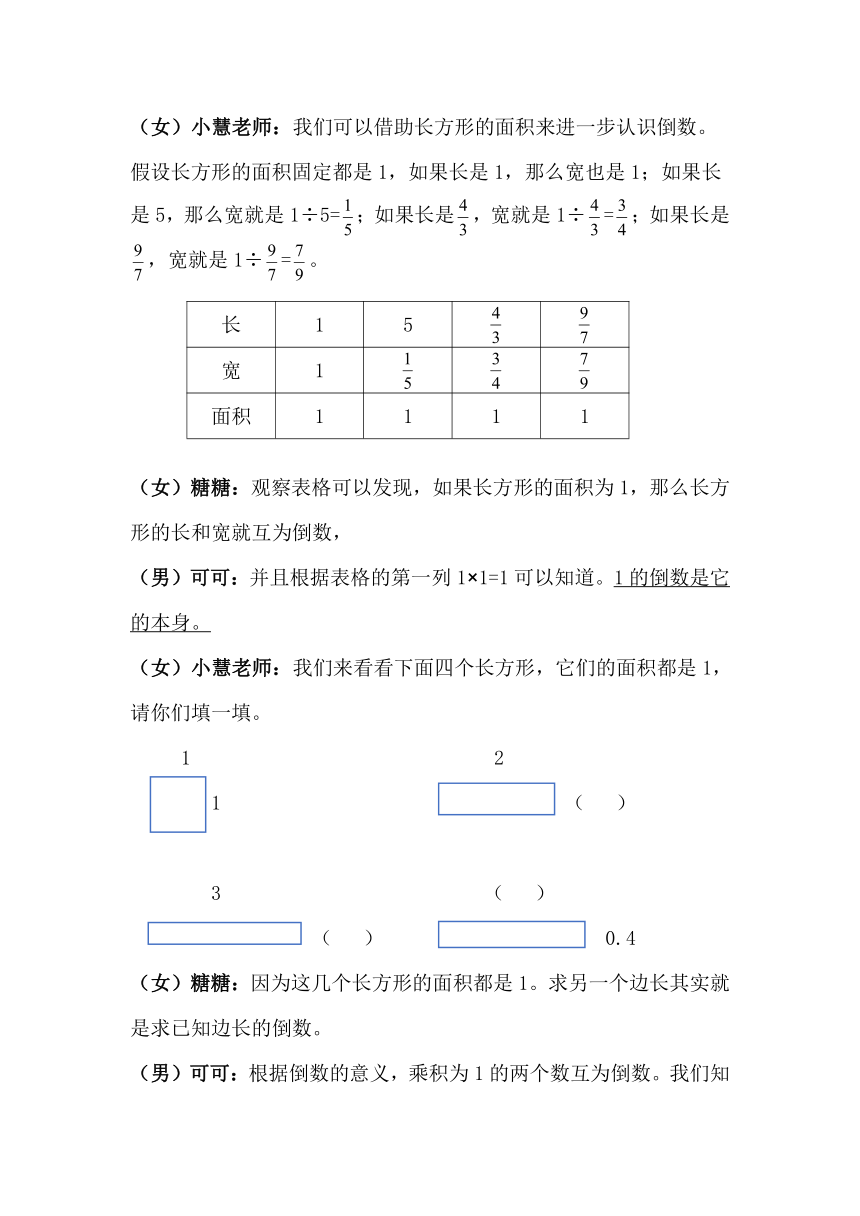
(女)小慧老师:我们可以借助长方形的面积来进一步认识倒数。
假设长方形的面积固定都是1,如果长是1,那么宽也是1;如果长是5,那么宽就是1÷5=;如果长是,宽就是1÷=;如果长是,宽就是1÷=。
长 1 5
宽 1
面积 1 1 1 1
(女)糖糖:观察表格可以发现,如果长方形的面积为1,那么长方形的长和宽就互为倒数,
(男)可可:并且根据表格的第一列1×1=1可以知道。1的倒数是它的本身。
(女)小慧老师:我们来看看下面四个长方形,它们的面积都是1,请你们填一填。
1 2
1 ( )
3 ( )
( ) 0.4
(女)糖糖:因为这几个长方形的面积都是1。求另一个边长其实就是求已知边长的倒数。
(男)可可:根据倒数的意义,乘积为1的两个数互为倒数。我们知道互为倒数的两个数的分子、分母相互颠倒,所以求一个数的倒数只需要把这个数的分子、分母交换位置就可以了。
(女)糖糖:1=,分子、分母交换位置是,所以1的倒数是它本身。
(男)可可:2=,分子、分母交换位置是,所以2的倒数是。
(女)糖糖:3=,分子、分母交换位置是,所以3的倒数是。
(男)可可:0.4=,分子、分母交换位置是,所以0.4的倒数是。
(女)小慧老师:看来你们已经掌握了倒数的意义以及如何求一个数的倒数的方法。我这儿还有一个问题:0有倒数吗?
(女)糖糖:根据倒数的意义:乘积为1的两个数互为倒数,0乘任何数都得0。所以0没有倒数。
(男)可可:根据求倒数的方法可知:0=,分子、分母交换位置是,0不能做分母(除数)。所以0没有倒数。
(女)小慧老师:那么现在我们一起总结一下这节课学习了那些内容。
(女)糖糖:我们学习了倒数的特点:
①乘积是1的两个数互为倒数。
②互为倒数的两个数的分子、分母相互颠倒。
③整数可以看成分母是1的分数。
④1的倒数是它的本身。
⑤0没有倒数。
(男)可可:学会了求一个数(0除外)的倒数的方法:(录音时表格里的内容要读出来)
求真分数和假分数的倒数时 交换分子、分母的位置
求整数(0除外)的倒数时 整数分之一
求小数的倒数时 先把小数化成分数, 再交换分子、分母的位置
小慧老师:现在你们的疑惑都解开了吧,要上课了,你们赶快回教室吧。
旁白:课间的时候,糖糖去找可可玩,发现可可眉头紧锁,一脸的疑惑,她赶紧去询问原因,想帮可可解决麻烦,等可可说了自己的问题后她也是一筹莫展,最后他们决定一起去找小慧老师帮忙。
可可:老师您好,我们遇到了一点麻烦,想请您指导一下我们。
小慧老师:我们的“小诸葛”也有麻烦了,说出来我们一起解决。
可可:我在做练习的时候,遇到了这样一组算式:(配音要读以下算式)
×=1 2×=1 ×=1
×10=1 ×=1 7×=1
我发现它们的结果都是1,感觉很奇怪,但是又总结不出其中的规律。
(女)小慧老师:除了结果都是1之外,这些算式还有哪些相同的特点呢?
(女)糖糖:我看出来了,我把以上算式中的整数看成分母是1的分数。发现每个算式中两个乘数的分子、分母交换了位置。
(女)糖糖:所以这六道算式有两个特点①两个数的乘积都是1。②两个乘数的分子,分母相互颠倒(dao第三声)。
(女)小慧老师:糖糖总结的很好,通常我们称乘积为1的两个数互为倒(dao第四声)数。
(女)小慧老师:倒数是指两个数字之间相互依存的一种关系。必须说,一个数是另一个数的倒数。不能孤立的说,某一个数是倒数。这是一个新的概念,你们还没有接触到。
(女)小慧老师:我们可以借助长方形的面积来进一步认识倒数。
假设长方形的面积固定都是1,如果长是1,那么宽也是1;如果长是5,那么宽就是1÷5=;如果长是,宽就是1÷=;如果长是,宽就是1÷=。
长 1 5
宽 1
面积 1 1 1 1
(女)糖糖:观察表格可以发现,如果长方形的面积为1,那么长方形的长和宽就互为倒数,
(男)可可:并且根据表格的第一列1×1=1可以知道。1的倒数是它的本身。
(女)小慧老师:我们来看看下面四个长方形,它们的面积都是1,请你们填一填。
1 2
1 ( )
3 ( )
( ) 0.4
(女)糖糖:因为这几个长方形的面积都是1。求另一个边长其实就是求已知边长的倒数。
(男)可可:根据倒数的意义,乘积为1的两个数互为倒数。我们知道互为倒数的两个数的分子、分母相互颠倒,所以求一个数的倒数只需要把这个数的分子、分母交换位置就可以了。
(女)糖糖:1=,分子、分母交换位置是,所以1的倒数是它本身。
(男)可可:2=,分子、分母交换位置是,所以2的倒数是。
(女)糖糖:3=,分子、分母交换位置是,所以3的倒数是。
(男)可可:0.4=,分子、分母交换位置是,所以0.4的倒数是。
(女)小慧老师:看来你们已经掌握了倒数的意义以及如何求一个数的倒数的方法。我这儿还有一个问题:0有倒数吗?
(女)糖糖:根据倒数的意义:乘积为1的两个数互为倒数,0乘任何数都得0。所以0没有倒数。
(男)可可:根据求倒数的方法可知:0=,分子、分母交换位置是,0不能做分母(除数)。所以0没有倒数。
(女)小慧老师:那么现在我们一起总结一下这节课学习了那些内容。
(女)糖糖:我们学习了倒数的特点:
①乘积是1的两个数互为倒数。
②互为倒数的两个数的分子、分母相互颠倒。
③整数可以看成分母是1的分数。
④1的倒数是它的本身。
⑤0没有倒数。
(男)可可:学会了求一个数(0除外)的倒数的方法:(录音时表格里的内容要读出来)
求真分数和假分数的倒数时 交换分子、分母的位置
求整数(0除外)的倒数时 整数分之一
求小数的倒数时 先把小数化成分数, 再交换分子、分母的位置
小慧老师:现在你们的疑惑都解开了吧,要上课了,你们赶快回教室吧。
