函数的单调性(新)
图片预览





文档简介
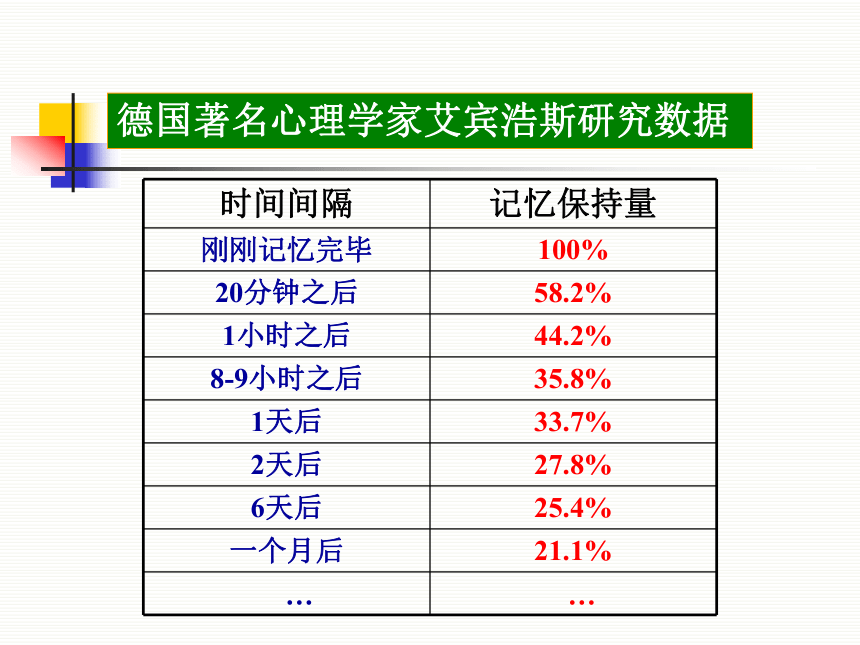
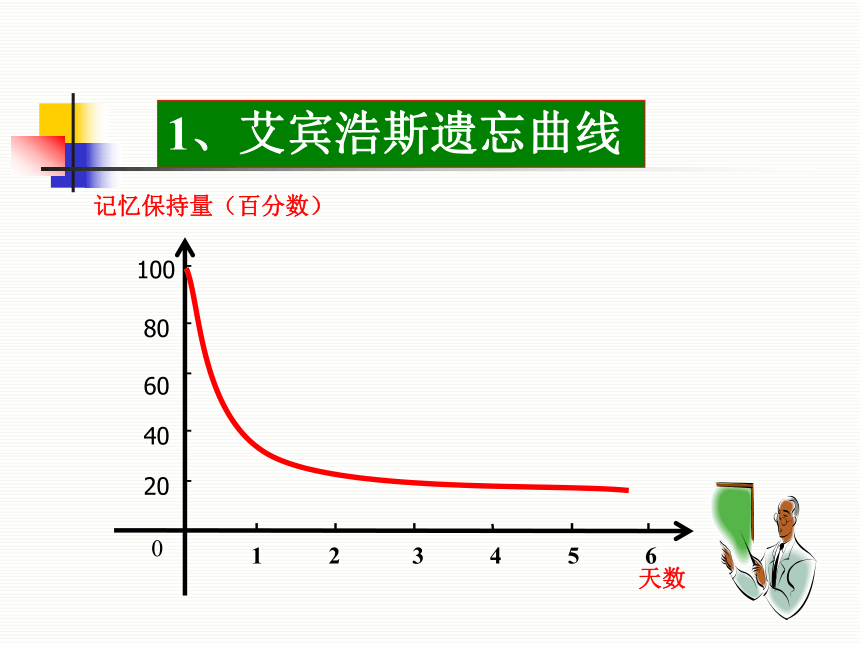
课件33张PPT。 德国有一位著名的心理学家名叫艾宾浩斯(Hermann Ebbinghaus,1850-1909),他在1879-1880年的记忆实验中用无意义音节来进行记忆研究。研究的中心问题之一就是学习后记忆保持量的变化规律。他以自己为实验对象,共做了163次实验. Hermann Ebbinghaus德国著名心理学家艾宾浩斯研究数据 1、艾宾浩斯遗忘曲线
函数的单调性与最大(小)值
( 第一课时)讲课人:教学目标(思想方法)通过自主探究活动,体验数学概念形成过程的真谛,学会运用函数图像理解和研究函数的性质;
(具体内容)
①理解并掌握函数的单调性及其几何意义;
②会求函数的单调区间;
③掌握用定义证明函数单调性的步骤,提高运用知识解决问题的能力;
问题讨论 问题1、 作出①y=x+1②y=-2x+2③ 函数的图象,并指出图象的变化趋势: 问题2、你能明确地说出上述图像的变化趋势的意思吗? 问题3、如何用数学语言表述一个函数是增函数呢? 问题4、如何用数学语言表述一个函数是减函数呢?
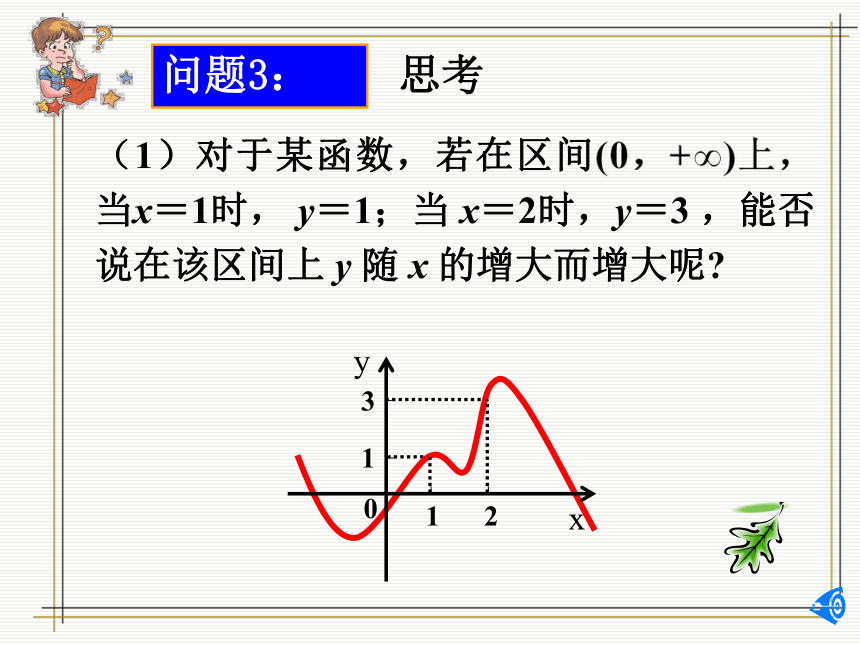
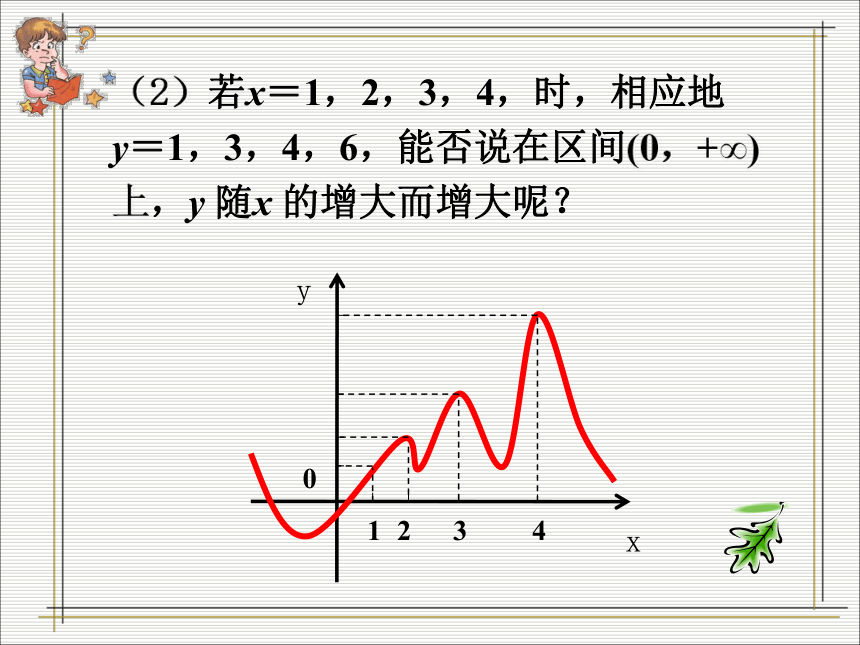
(1)对于某函数,若在区间(0,+∞)上,当x=1时, y=1;当 x=2时,y=3 ,能否说在该区间上 y 随 x 的增大而增大呢?问题3:思考(2)若x=1,2,3,4,时,相应地 y=1,3,4,6,能否说在区间(0,+∞)上,y 随x 的增大而增大呢?
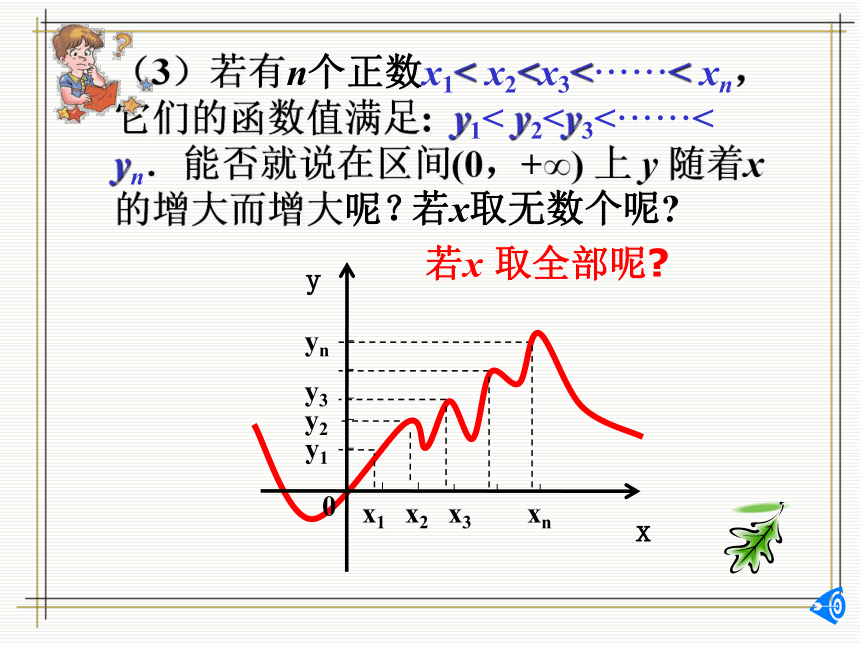
(3)若有n个正数x1< x2练1、画出下列函数图象,并写出单调区间:
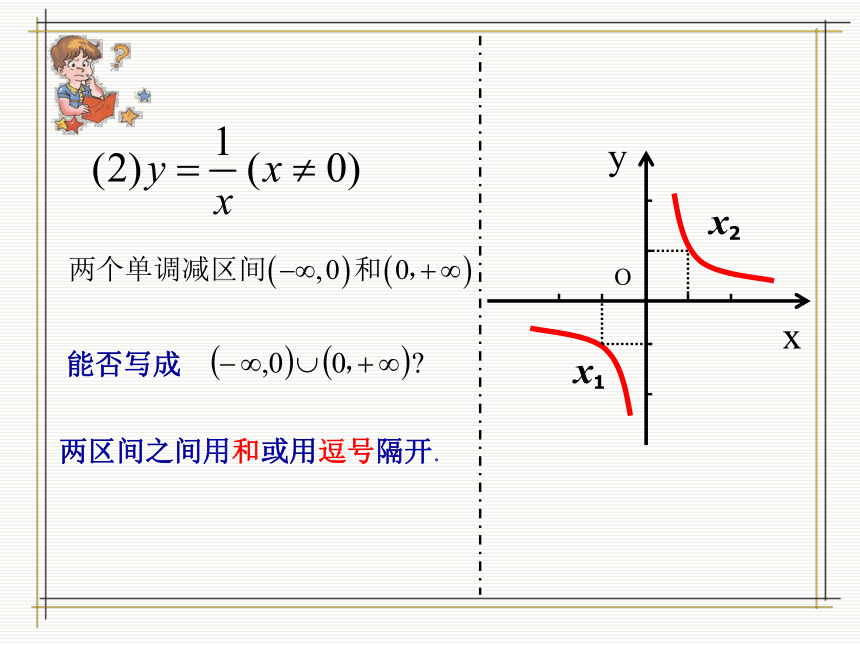
两区间之间用和或用逗号隔开. 能否写成x1x2 例2:证明函数
在区间 上是减函数..布置作业必做: P38 习题 2.3 A组2、3、4 (2) 研究 的单调性,
并给出证明,试求出该函数的值域。选做(1)判断函数
在区间 上的单调性。 再 见问题1、 作出下列函数的图象,并指出图象的变化趋势:问题2、你能明确地说出“图象呈逐渐上升或下降趋势”的意思吗?在某一区间内,图象在该区间呈上升趋势图象在该区间呈下降趋势函数的这种性质称为函数的单调性。 问题3、如何用数学语言表述一个函数是增函数呢? 0 X X不断增大,f(x)也不断增大0 XYX1X2f(X1)f(X2) 问题3、如何用数学语言表述一个函数是增函数呢? 问题4:如何定义一个函数是单调减函数?减函数定义
如果函数y=f(x)在区间I是单调增函数或单调减函数,那么就说函数y=f(x)在区间I上具有单调性.
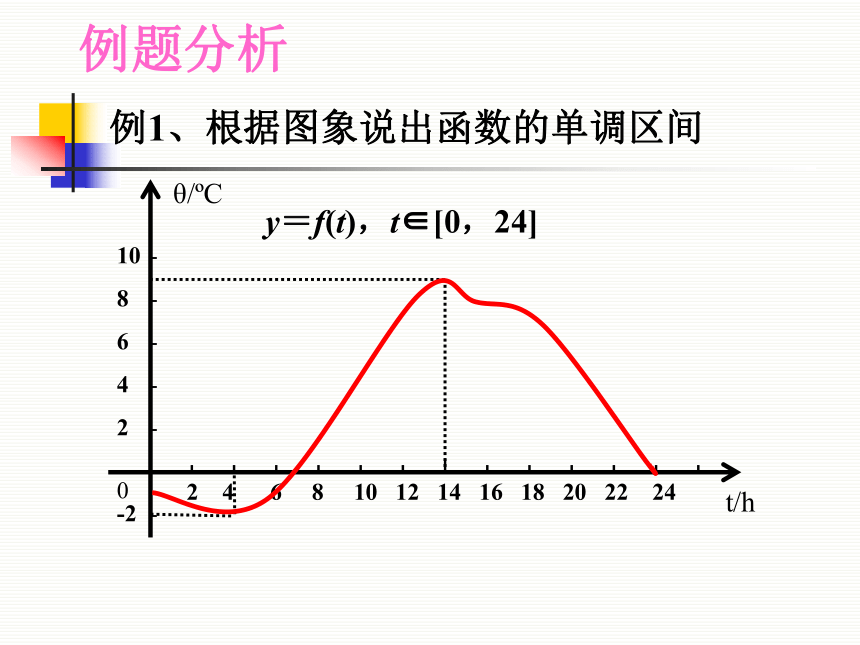
单调增区间和单调减区间统称为单调区间.单调区间y=f(x),x∈[0,24]例1、根据图象说出函数的单调区间[0,4][4,14][14,24]例题分析
例2、画出下列函数图象,并写出单调区间:
两区间之间用和或用逗号隔开. 能否写成x1x2(1)怎样证明?证明:设 是(0,+∞)上的任意
两个实数,且 .
课堂练习1:填表函数单调区间k >0k <0k >0k <0增函数减函数减函数增函数单调性
函数单调区间单调性增函数增函数练习2:填表(二)减函数减函数证明:(设量)(比较)(结论)(定号) 练习3:证明函数
在区间 上是减函数..2、函数单调性的定义;4、证明函数单调性的步骤. 归纳总结本节课主要学习了以下内容:3、判断单调性的方法:图象、定义;1、单调函数的图象特征;设量定大小;作差定符号;判断定结论。
函数的单调性与最大(小)值
( 第一课时)讲课人:教学目标(思想方法)通过自主探究活动,体验数学概念形成过程的真谛,学会运用函数图像理解和研究函数的性质;
(具体内容)
①理解并掌握函数的单调性及其几何意义;
②会求函数的单调区间;
③掌握用定义证明函数单调性的步骤,提高运用知识解决问题的能力;
问题讨论 问题1、 作出①y=x+1②y=-2x+2③ 函数的图象,并指出图象的变化趋势: 问题2、你能明确地说出上述图像的变化趋势的意思吗? 问题3、如何用数学语言表述一个函数是增函数呢? 问题4、如何用数学语言表述一个函数是减函数呢?
(1)对于某函数,若在区间(0,+∞)上,当x=1时, y=1;当 x=2时,y=3 ,能否说在该区间上 y 随 x 的增大而增大呢?问题3:思考(2)若x=1,2,3,4,时,相应地 y=1,3,4,6,能否说在区间(0,+∞)上,y 随x 的增大而增大呢?
(3)若有n个正数x1< x2
两区间之间用和或用逗号隔开. 能否写成x1x2 例2:证明函数
在区间 上是减函数..布置作业必做: P38 习题 2.3 A组2、3、4 (2) 研究 的单调性,
并给出证明,试求出该函数的值域。选做(1)判断函数
在区间 上的单调性。 再 见问题1、 作出下列函数的图象,并指出图象的变化趋势:问题2、你能明确地说出“图象呈逐渐上升或下降趋势”的意思吗?在某一区间内,图象在该区间呈上升趋势图象在该区间呈下降趋势函数的这种性质称为函数的单调性。 问题3、如何用数学语言表述一个函数是增函数呢? 0 X X不断增大,f(x)也不断增大0 XYX1X2f(X1)f(X2) 问题3、如何用数学语言表述一个函数是增函数呢? 问题4:如何定义一个函数是单调减函数?减函数定义
如果函数y=f(x)在区间I是单调增函数或单调减函数,那么就说函数y=f(x)在区间I上具有单调性.
单调增区间和单调减区间统称为单调区间.单调区间y=f(x),x∈[0,24]例1、根据图象说出函数的单调区间[0,4][4,14][14,24]例题分析
例2、画出下列函数图象,并写出单调区间:
两区间之间用和或用逗号隔开. 能否写成x1x2(1)怎样证明?证明:设 是(0,+∞)上的任意
两个实数,且 .
课堂练习1:填表函数单调区间k >0k <0k >0k <0增函数减函数减函数增函数单调性
函数单调区间单调性增函数增函数练习2:填表(二)减函数减函数证明:(设量)(比较)(结论)(定号) 练习3:证明函数
在区间 上是减函数..2、函数单调性的定义;4、证明函数单调性的步骤. 归纳总结本节课主要学习了以下内容:3、判断单调性的方法:图象、定义;1、单调函数的图象特征;设量定大小;作差定符号;判断定结论。
