2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册6.2排列组合之分组分配问题课件(共23张PPT)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册6.2排列组合之分组分配问题课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 18:35:13 | ||
图片预览





文档简介
(共23张PPT)
6.2 排列组合之分组分配问题
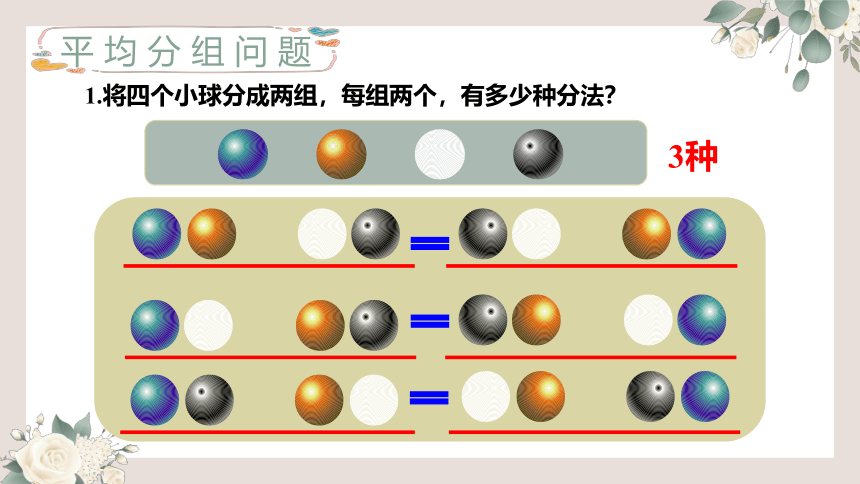
1.将四个小球分成两组,每组两个,有多少种分法?
3种
平均分组问题
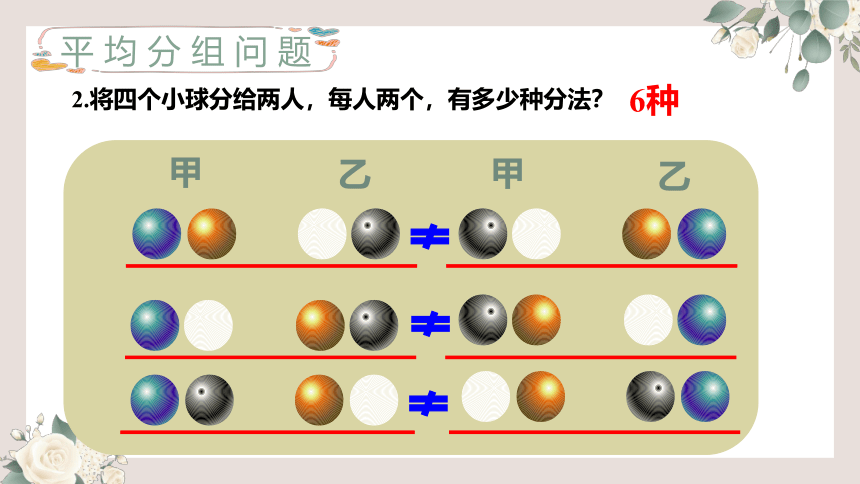
2.将四个小球分给两人,每人两个,有多少种分法?
甲
甲
乙
乙
6种
平均分组问题
平均分组问题
类型一 平均分组问题
1.平均分成的组,不管它们的顺序如何,都是一种情况,所以分组后要除以 ,即m!,其中m表示组数.
(2)有分配对象: 把 n 个不同的元素分成有序的 m 组,每组 r 个元素,则共有 种分法.(其中 mr = n)
(1)无分配对象: 把 n 个不同的元素分成无序的 m 组,每组 r 个元素,则共有 种分法.(其中 mr = n)
2.平均分组问题以有无分配对象分成两类:
平均分组无分配对象的问题
1. 12本不同的书按4: 4: 4平均分成三堆有多少种不同的分法?
小试牛刀
2. 6本不同的书按2: 2: 2平均分给甲、乙、丙三个人,有多少种不同的分法?
平均分组有分配对象的问题
6种
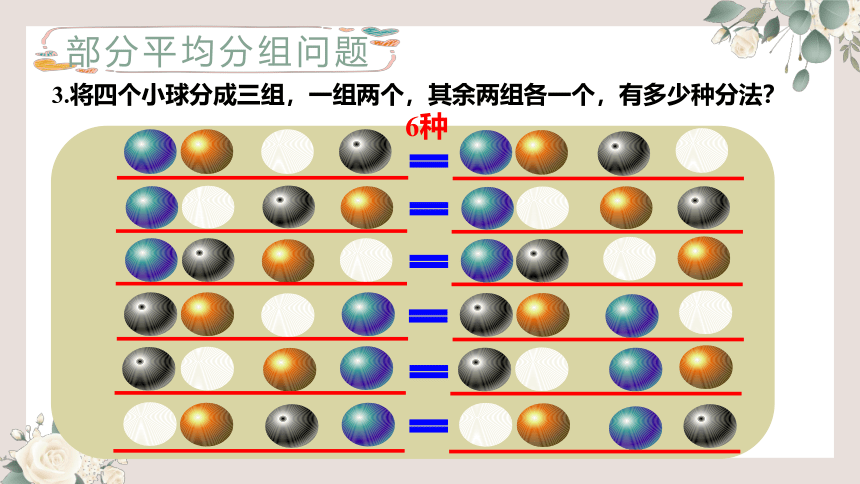
部分平均分组问题
3.将四个小球分成三组,一组两个,其余两组各一个,有多少种分法?
12种
部分平均分组问题
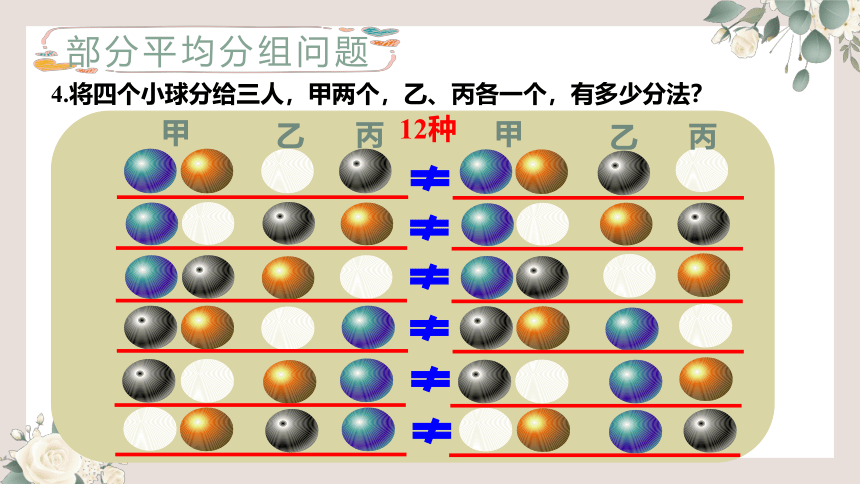
4.将四个小球分给三人,甲两个,乙、丙各一个,有多少分法?
甲
乙
丙
甲
乙
丙
类型二 部分平均分组问题
部分平均分组问题
部分平均分组问题以有无分配对象分成两类:
(1)无分配对象: 把 n 个不同的元素分成 m 组,其中 m1 个组有 r1 个元素, m2 个组有 r2 个元素,……, mk 个组有 rk 个元素,则共有
种分法.(其中m1r1+m2r2+m3r3+…+mkrk=n)
(2)有分配对象: 把 n 个不同的元素分成 m 组,其中 m1 个组有 r1 个元素,m2 个组有 r2 个元素,……, mk 个组有 rk 个元素,并且分配给 m 人,则共有
种分法.(其中m1r1+m2r2+m3r3+…+mkrk=n)
部分平均分组有分配对象的问题
2. 12支笔按3 : 3 : 2 : 2 : 2分给A, B, C, D, E五个人有多少种不同的分法?
注: 先分组再排列. 分成的组数看成元素的个数,把部分均分的五组看成是五个元素在五个位置上作排列.
小试牛刀
1. 六本不同的书分成3组,一组4本其余各1本,有多少种分法?
部分平均分组无分配对象的问题
5.将四个小球分成两组,一组三个,一组一个,有多少分法?
4种
非平均分组问题
6.将四个小球分给两人,一人三个, 一人一个,有多少分法?
8种
非平均分组问题
甲
乙
甲
乙
(1)无分配对象或有分配对象且确定: 把 n 个不同的元素分成 m 组,第1组 r1 个元素,第2组 r2 个元素,第3组 r3 个元素,……第m组 rm 个元素,则共有 种分法.(其中r1+r2+r3+…+rm=n)
(2)有分配对象且不确定: 把 n 个不同的元素分成 m 组,第1组 r1 个元素,第2组 r2 个元素,第3组 r3 个元素,……第 m 组 rm 个元素,再分给 m 个人,则共有 种分法.(其中r1+r2+r3+…+rm=n)
非平均分组问题
类型三 非平均分组问题
非平均分组问题以有无分配对象,分配对象是否确定分成两类:
小试牛刀
1. 六本不同的书按1∶2∶3分成三堆有多少种不同的分法?
非平均分组无分配对象问题
2. 六本不同的书分给3人,甲1本、乙2本、丙3本,有多少种不同的分法?
非平均分组分配对象确定问题
3.六本不同的书分给三人,1人1本,1人2本,1人3本有多少种分法?
非平均分组分配对象不确定问题
注:非平均分问题无分配对象只要按比例分完再用乘法原理作积.
注:非均分组有确定分配对象要把组数当作元素个数, 此与非均分组无分配对象结果一样.
有6本不同的书,分成4堆.
(1)如果一堆3本,其余各堆各1本,有多少种分法?
(2)如果每堆至多2本,至少1本,有多少种分法?
巩固练习
2. 六本不同的书分给3 个人,按要求有多少种不同的分法?
(1)平均分给甲、乙、丙三人;
(2)分给甲一本,乙两本,丙三本;
(3)分给三个人,一人一本,一人两本,一人三本;
巩固练习
注:若分成的 m 组是有组别的,只需在原来的分组基础上再
(4)分给甲四本,乙、丙各一本;
(5)分给三个人,一人四本,其余两人各一本;
(6)分给甲乙丙三人,每人至少一本.
1,1,4
1,2,3
2,2,2
巩固练习
3. 9件不同的玩具,按下列方案有几种分法? (1)甲得2件,乙得3件,丙得4件,有多少种分法?
(2)一人得2件,一人得3件,一人得4件,有多少种分法?
(3)每人3件,有多少种分法?
(4)平均分成三堆,有多少种分法?
(5)分为2、2、2、3四堆,有多少种分法?
巩固练习
4.(1)今有10件不同奖品, 从中选6件分成三份, 二份各1件,另一份4件, 有多少种分法
(2) 今有10件不同奖品, 从中选6件分给甲乙丙三人, 每人二件有多少种分法
巩固练习
1.将6个相同的小球放入4个编号为1,2,3,4的盒子,求下列方法的种数.
(1)每个盒子都不空;
(2)恰有一个空盒子;
(3)恰有两个空盒子.
拓展练习
相同元素分配问题
解: (1)先把6个相同的小球排成一行,然后在小球之间的5个空隙中任选3个空隙各插一块隔板,故共有 (种)放法.
(2)第一步先选出一个盒子,有 种选法;
第二步在小球之间5个空隙中任选2个空隙各插一块隔板,有 种插法;
由分步乘法计数原理,共有 种放法.
“隔板法”专门解决“相同元素” 的分配问题. n个元素插入m块隔板的方法数为 .
1.将6个相同的小球放入4个编号为1,2,3,4的盒子,求下列方法的种数.
(3)恰有两个空盒子.
拓展练习
相同元素分配问题
解:(3)第一步先在6个小球之间的5个空隙中任选1个空隙插一块隔板,有 种插法;
第二步分成两类:
由计数原理,共有 种放法.
①两块隔板不相邻,有左端、第一块隔板、右端这三个位置,有 种插法;
②两块隔板相邻,有左端、第一块隔板、右端这三个位置,有 种插法;
2.有4个不同的球,4个不同的盒子,问:
(1)把球全部放到盒子内,共有几种放法
(2)恰有一个空盒,共有多少种放法?
(3)恰有2个空盒,共有多少种放法?
拓展练习
不相同元素分配问题
3.(1) 6本不同的书全部分给5个人,有多少种分法?
(2) 5本不同的书全部分给6个人,每人至多一本,有多少种分法?
(3) 5本相同的书全部分给6个人,每人至多一本,有多少种分法?
(4) 3本相同的书全部分给5个人,有多少种分法?
拓展练习
课堂小结
说明: 提出分组与分配问题,澄清模糊概念:
分组问题:将 n 个不同元素按照某些条件分成 k 组,称为分组问题. 分组问题有不平均分组、平均分组、和部分平均分组三种情况.
分配问题:将 n 个不同元素按照某些条件分配给 k 个不同的对象,称为分配问题,分定向分配和不定向分配两种问题.
分组问题和分配问题是有区别的,前者组与组之间只要元素个数相同是不区分的; 而后者即使 2 组元素个数相同,但因对象不同,仍然是可区分的. 对于后者必须先分组后排列.
6.2 排列组合之分组分配问题
1.将四个小球分成两组,每组两个,有多少种分法?
3种
平均分组问题
2.将四个小球分给两人,每人两个,有多少种分法?
甲
甲
乙
乙
6种
平均分组问题
平均分组问题
类型一 平均分组问题
1.平均分成的组,不管它们的顺序如何,都是一种情况,所以分组后要除以 ,即m!,其中m表示组数.
(2)有分配对象: 把 n 个不同的元素分成有序的 m 组,每组 r 个元素,则共有 种分法.(其中 mr = n)
(1)无分配对象: 把 n 个不同的元素分成无序的 m 组,每组 r 个元素,则共有 种分法.(其中 mr = n)
2.平均分组问题以有无分配对象分成两类:
平均分组无分配对象的问题
1. 12本不同的书按4: 4: 4平均分成三堆有多少种不同的分法?
小试牛刀
2. 6本不同的书按2: 2: 2平均分给甲、乙、丙三个人,有多少种不同的分法?
平均分组有分配对象的问题
6种
部分平均分组问题
3.将四个小球分成三组,一组两个,其余两组各一个,有多少种分法?
12种
部分平均分组问题
4.将四个小球分给三人,甲两个,乙、丙各一个,有多少分法?
甲
乙
丙
甲
乙
丙
类型二 部分平均分组问题
部分平均分组问题
部分平均分组问题以有无分配对象分成两类:
(1)无分配对象: 把 n 个不同的元素分成 m 组,其中 m1 个组有 r1 个元素, m2 个组有 r2 个元素,……, mk 个组有 rk 个元素,则共有
种分法.(其中m1r1+m2r2+m3r3+…+mkrk=n)
(2)有分配对象: 把 n 个不同的元素分成 m 组,其中 m1 个组有 r1 个元素,m2 个组有 r2 个元素,……, mk 个组有 rk 个元素,并且分配给 m 人,则共有
种分法.(其中m1r1+m2r2+m3r3+…+mkrk=n)
部分平均分组有分配对象的问题
2. 12支笔按3 : 3 : 2 : 2 : 2分给A, B, C, D, E五个人有多少种不同的分法?
注: 先分组再排列. 分成的组数看成元素的个数,把部分均分的五组看成是五个元素在五个位置上作排列.
小试牛刀
1. 六本不同的书分成3组,一组4本其余各1本,有多少种分法?
部分平均分组无分配对象的问题
5.将四个小球分成两组,一组三个,一组一个,有多少分法?
4种
非平均分组问题
6.将四个小球分给两人,一人三个, 一人一个,有多少分法?
8种
非平均分组问题
甲
乙
甲
乙
(1)无分配对象或有分配对象且确定: 把 n 个不同的元素分成 m 组,第1组 r1 个元素,第2组 r2 个元素,第3组 r3 个元素,……第m组 rm 个元素,则共有 种分法.(其中r1+r2+r3+…+rm=n)
(2)有分配对象且不确定: 把 n 个不同的元素分成 m 组,第1组 r1 个元素,第2组 r2 个元素,第3组 r3 个元素,……第 m 组 rm 个元素,再分给 m 个人,则共有 种分法.(其中r1+r2+r3+…+rm=n)
非平均分组问题
类型三 非平均分组问题
非平均分组问题以有无分配对象,分配对象是否确定分成两类:
小试牛刀
1. 六本不同的书按1∶2∶3分成三堆有多少种不同的分法?
非平均分组无分配对象问题
2. 六本不同的书分给3人,甲1本、乙2本、丙3本,有多少种不同的分法?
非平均分组分配对象确定问题
3.六本不同的书分给三人,1人1本,1人2本,1人3本有多少种分法?
非平均分组分配对象不确定问题
注:非平均分问题无分配对象只要按比例分完再用乘法原理作积.
注:非均分组有确定分配对象要把组数当作元素个数, 此与非均分组无分配对象结果一样.
有6本不同的书,分成4堆.
(1)如果一堆3本,其余各堆各1本,有多少种分法?
(2)如果每堆至多2本,至少1本,有多少种分法?
巩固练习
2. 六本不同的书分给3 个人,按要求有多少种不同的分法?
(1)平均分给甲、乙、丙三人;
(2)分给甲一本,乙两本,丙三本;
(3)分给三个人,一人一本,一人两本,一人三本;
巩固练习
注:若分成的 m 组是有组别的,只需在原来的分组基础上再
(4)分给甲四本,乙、丙各一本;
(5)分给三个人,一人四本,其余两人各一本;
(6)分给甲乙丙三人,每人至少一本.
1,1,4
1,2,3
2,2,2
巩固练习
3. 9件不同的玩具,按下列方案有几种分法? (1)甲得2件,乙得3件,丙得4件,有多少种分法?
(2)一人得2件,一人得3件,一人得4件,有多少种分法?
(3)每人3件,有多少种分法?
(4)平均分成三堆,有多少种分法?
(5)分为2、2、2、3四堆,有多少种分法?
巩固练习
4.(1)今有10件不同奖品, 从中选6件分成三份, 二份各1件,另一份4件, 有多少种分法
(2) 今有10件不同奖品, 从中选6件分给甲乙丙三人, 每人二件有多少种分法
巩固练习
1.将6个相同的小球放入4个编号为1,2,3,4的盒子,求下列方法的种数.
(1)每个盒子都不空;
(2)恰有一个空盒子;
(3)恰有两个空盒子.
拓展练习
相同元素分配问题
解: (1)先把6个相同的小球排成一行,然后在小球之间的5个空隙中任选3个空隙各插一块隔板,故共有 (种)放法.
(2)第一步先选出一个盒子,有 种选法;
第二步在小球之间5个空隙中任选2个空隙各插一块隔板,有 种插法;
由分步乘法计数原理,共有 种放法.
“隔板法”专门解决“相同元素” 的分配问题. n个元素插入m块隔板的方法数为 .
1.将6个相同的小球放入4个编号为1,2,3,4的盒子,求下列方法的种数.
(3)恰有两个空盒子.
拓展练习
相同元素分配问题
解:(3)第一步先在6个小球之间的5个空隙中任选1个空隙插一块隔板,有 种插法;
第二步分成两类:
由计数原理,共有 种放法.
①两块隔板不相邻,有左端、第一块隔板、右端这三个位置,有 种插法;
②两块隔板相邻,有左端、第一块隔板、右端这三个位置,有 种插法;
2.有4个不同的球,4个不同的盒子,问:
(1)把球全部放到盒子内,共有几种放法
(2)恰有一个空盒,共有多少种放法?
(3)恰有2个空盒,共有多少种放法?
拓展练习
不相同元素分配问题
3.(1) 6本不同的书全部分给5个人,有多少种分法?
(2) 5本不同的书全部分给6个人,每人至多一本,有多少种分法?
(3) 5本相同的书全部分给6个人,每人至多一本,有多少种分法?
(4) 3本相同的书全部分给5个人,有多少种分法?
拓展练习
课堂小结
说明: 提出分组与分配问题,澄清模糊概念:
分组问题:将 n 个不同元素按照某些条件分成 k 组,称为分组问题. 分组问题有不平均分组、平均分组、和部分平均分组三种情况.
分配问题:将 n 个不同元素按照某些条件分配给 k 个不同的对象,称为分配问题,分定向分配和不定向分配两种问题.
分组问题和分配问题是有区别的,前者组与组之间只要元素个数相同是不区分的; 而后者即使 2 组元素个数相同,但因对象不同,仍然是可区分的. 对于后者必须先分组后排列.
