人教版七年级数学下册 8.4 三元一次方程组的解法 课件(共15张PPT)
文档属性
| 名称 | 人教版七年级数学下册 8.4 三元一次方程组的解法 课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 520.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 14:19:44 | ||
图片预览






文档简介
(共15张PPT)
8.4三元一次方程组
的解法
1.解方程组的基本思想就是“消元”思想,即将“多元”化为“一元”的思想.
2.会用代入法或加减法解二元一次方程组.
小明手头有12张面额分别是1元、2元、5元的纸币,共计22元,其中1元纸币的数量是2元纸币数量的4倍.求1元、2元、5元的纸币各多少张?
这个问题中包含有 个相等关系:
分析
三
1元纸币张数+2元纸币张数+5元纸币张数=12张
1元纸币的张数=2元纸币的张数的4倍
1元的金额+2元的金额+5元的金额=22元
问题
我们自然的想法是,设1元、2元、5元的纸币分别为x张、y张、 z张,根据题意可以得到下面三个方程:
x+y+z=12, x+2y+5z=22, x=4y.
这个问题的解必须同时满足上面三个条件,因此,我们把三个方程合在一起写成
定义
这个方程组含有三个未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,像这样的方程组叫做三元一次方程组.
讨论:怎样解三元一次方程组?
能不能类比二元一次方程组的解法,设法消去一个或两个未知数,把它化成二元一次方程组或二元一次方程呢
①
②
③
仿照前面学过的代入法,可以把③分别代入①②,得到两个只含y,z的方程
这个方程组就是我们上节学过的二元一次方程组。
即
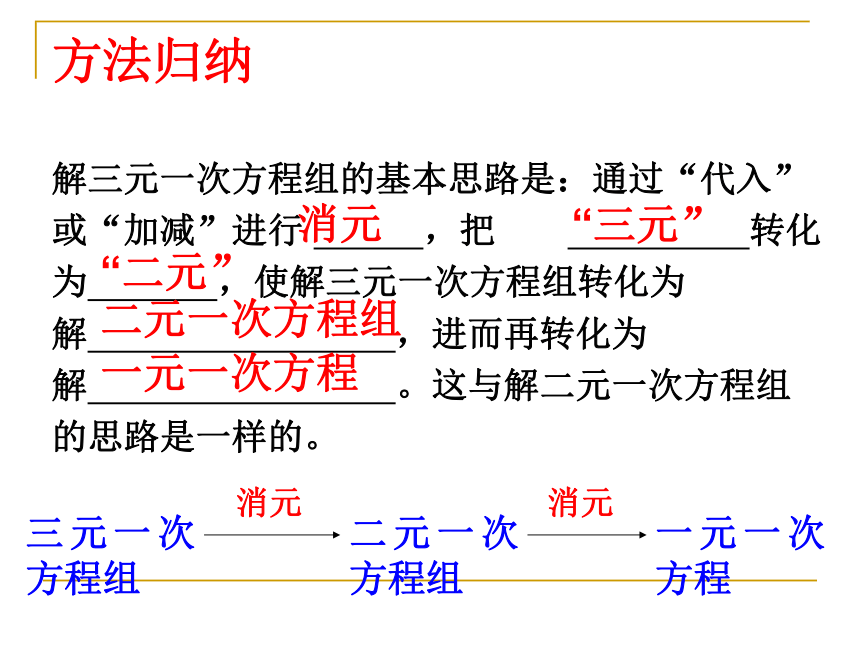
方法归纳
解三元一次方程组的基本思路是:通过“代入”
或“加减”进行 ,把 转化
为 ,使解三元一次方程组转化为
解 ,进而再转化为
解 。这与解二元一次方程组
的思路是一样的。
消元
“三元”
“二元”
二元一次方程组
一元一次方程
三元一次方程组
二元一次方程组
一元一次方程
消元
消元
例1:解三元一次方程组
①
②
③
解:②×3+③得:11x+10z=35 ④
①与④组成方程组
解得:
把x=5,z=-2代入②得:y=
∴
怎样解三元一次方程组?
分析:方程①只含x,z,因此,可由②③消去y,得到一个只含x,z的方程,与①组成一个二元一次方程组.
不解方程组,指出下列方程组中先消去哪个未知数,使得求解方程组较为简便
解方程组:
解:①+②+③得:x+y+z=45 ④
①
②
③
④-①得:z=18
④-②得:x=12
④-③得:y=15
解方程组
例2 在等式 y=a +bx+c中,当x=-1时,y=0;当x=2时,
y=3;当x=5时,y=60. 求a,b,c的值
解:根据题意,得三元一次方程组
a-b+c= 0 ①
4a+2b+c=3 ②
25a+5b+c=60 ③
{
②-①, 得 a+b=1 ④
③-①,得 4a+b=10 ⑤
④与⑤组成二元一次方程组
a+b=1
4a+b=10
{
a=3
b=-2
解这个方程组,得
{
把 代入①,得
a=3
b=-2
{
C=-5
a=3
b=-2
c=-5
{
因此
答:a=3, b=-2, c=-5.
练习
解下列方程组:
(4)
(2)
(3)
1、一个方程组含有三个未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,这样的方程组叫做三元一次方程组
知识小结
2.基本思路:
三元方程组: 二元方程组
一元方程
消元
消元
②有表达式,用代入法。
③缺某元消某元
①消去某一元
3、解三元一次方程组有哪些方法?
8.4三元一次方程组
的解法
1.解方程组的基本思想就是“消元”思想,即将“多元”化为“一元”的思想.
2.会用代入法或加减法解二元一次方程组.
小明手头有12张面额分别是1元、2元、5元的纸币,共计22元,其中1元纸币的数量是2元纸币数量的4倍.求1元、2元、5元的纸币各多少张?
这个问题中包含有 个相等关系:
分析
三
1元纸币张数+2元纸币张数+5元纸币张数=12张
1元纸币的张数=2元纸币的张数的4倍
1元的金额+2元的金额+5元的金额=22元
问题
我们自然的想法是,设1元、2元、5元的纸币分别为x张、y张、 z张,根据题意可以得到下面三个方程:
x+y+z=12, x+2y+5z=22, x=4y.
这个问题的解必须同时满足上面三个条件,因此,我们把三个方程合在一起写成
定义
这个方程组含有三个未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,像这样的方程组叫做三元一次方程组.
讨论:怎样解三元一次方程组?
能不能类比二元一次方程组的解法,设法消去一个或两个未知数,把它化成二元一次方程组或二元一次方程呢
①
②
③
仿照前面学过的代入法,可以把③分别代入①②,得到两个只含y,z的方程
这个方程组就是我们上节学过的二元一次方程组。
即
方法归纳
解三元一次方程组的基本思路是:通过“代入”
或“加减”进行 ,把 转化
为 ,使解三元一次方程组转化为
解 ,进而再转化为
解 。这与解二元一次方程组
的思路是一样的。
消元
“三元”
“二元”
二元一次方程组
一元一次方程
三元一次方程组
二元一次方程组
一元一次方程
消元
消元
例1:解三元一次方程组
①
②
③
解:②×3+③得:11x+10z=35 ④
①与④组成方程组
解得:
把x=5,z=-2代入②得:y=
∴
怎样解三元一次方程组?
分析:方程①只含x,z,因此,可由②③消去y,得到一个只含x,z的方程,与①组成一个二元一次方程组.
不解方程组,指出下列方程组中先消去哪个未知数,使得求解方程组较为简便
解方程组:
解:①+②+③得:x+y+z=45 ④
①
②
③
④-①得:z=18
④-②得:x=12
④-③得:y=15
解方程组
例2 在等式 y=a +bx+c中,当x=-1时,y=0;当x=2时,
y=3;当x=5时,y=60. 求a,b,c的值
解:根据题意,得三元一次方程组
a-b+c= 0 ①
4a+2b+c=3 ②
25a+5b+c=60 ③
{
②-①, 得 a+b=1 ④
③-①,得 4a+b=10 ⑤
④与⑤组成二元一次方程组
a+b=1
4a+b=10
{
a=3
b=-2
解这个方程组,得
{
把 代入①,得
a=3
b=-2
{
C=-5
a=3
b=-2
c=-5
{
因此
答:a=3, b=-2, c=-5.
练习
解下列方程组:
(4)
(2)
(3)
1、一个方程组含有三个未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,这样的方程组叫做三元一次方程组
知识小结
2.基本思路:
三元方程组: 二元方程组
一元方程
消元
消元
②有表达式,用代入法。
③缺某元消某元
①消去某一元
3、解三元一次方程组有哪些方法?
