人教版七年级数学下册 8.3实际问题与二元一次方程组 课件(共15张PPT)
文档属性
| 名称 | 人教版七年级数学下册 8.3实际问题与二元一次方程组 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 795.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 14:20:34 | ||
图片预览






文档简介
(共15张PPT)
二元一次方程组的解法:
根据方程未知数的系数特征确定用哪一种解法.
基本思想或思路——
常用方法——
温顾而知新:
消元
代入消元法
加减消元法
8.3实际问题与二元一次方程组(1)
小街镇一中
王佳鹏
设问3:等量关系是什么呢?
设问1:本题需要大家解决什么问题呢?
设问2:你有什么办法?
先根据问题中给定的数量关系求出每头大牛和每头小牛1天各约需用饲料量,再来判断估计是否正确
(1)1天30头大牛所用的饲料+15头小牛的所用的饲料=675Kg
(2)1天42头大牛所用的饲料+20头小牛的所用的饲料=940Kg
判断李大叔的估计是否正确 ?
养牛场原有30头大牛和15头小牛,1天约用饲料675kg.一周后又购进12头大牛和5头小牛,这时1天约用饲料940kg.饲养员李大叔估计每头大牛1天约需饲料18~20kg,每头小牛1天约需饲料7~8kg,你能通过计算检验他的估计吗?
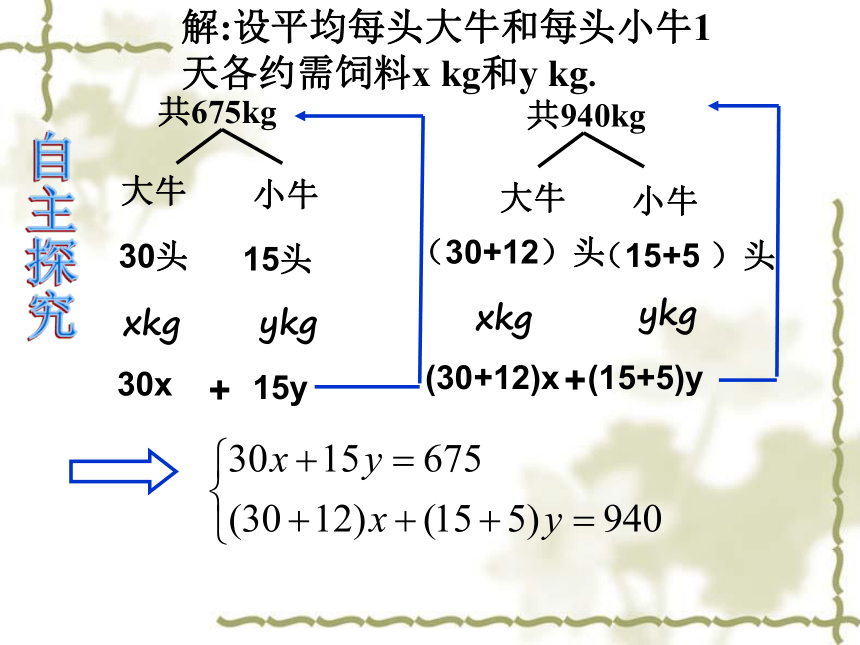
共675kg
大牛
小牛
30头
15头
xkg
ykg
30x
15y
+
共940kg
大牛
小牛
(30+12)头
(15+5 )头
xkg
ykg
(30+12)x
(15+5)y
+
解:设平均每头大牛和每头小牛1天各约需饲料x kg和y kg.
这就是说,每头大牛约需饲料20kg,每头小牛约需饲料5kg.因此,饲料员李大叔对大牛的食量估计较准确,对小牛的食量估计偏高
解得:
20
5
化简得:
①
②
解:设平均每头大牛和每头小牛1天各约需饲料xkg和ykg.
共675kg
大牛
小牛
30头
15头
xkg
ykg
30x
15y
+
共940kg
大牛
小牛
(30+12)头
(15+5 )头
xkg
ykg
12x + 5y
解:设平均每头大牛和每头小牛1天各约需饲料x kg和y kg.
共940-675=265kg
12
5
(30+12)x+(15+5)y
化简得:
列方程组解应用题的一般步骤:
(1)设:设未知数
(2)列:根据相等关系列出方程组;
(3)解:解所列方程组,得出未知数的值;
(4)验:检验所求未知数的值是否正确, 是否符合实际意义;
(5)答:写出答案.
某家商店的账目记录显示,某天卖出9支牙刷和6盒牙膏,收入60元;另一天,以同样的价格卖出同样的15支牙刷和10盒牙膏,收入90元。这个记录是否有误?如果有误,请说明理由。
共60元
牙刷
牙膏
9
6
x
y
9x
6y
+
共90元
牙刷
牙膏
15
10
x
y
15x
10y
+
解:设1支牙刷x元,1盒牙膏y元,
解: (1)设1支牙刷x元,1盒牙膏y元,
9x+6y=60
15x+10y=90
化简得:
3x+2y=20
3x+2y=18
此方程组无解,说明记录有误
答:这个记录有误。
①
②
某校共有3个大餐厅和2个小餐厅,经过测试:同时开放1个大餐厅和2个小餐厅,可供400名学生就餐;同时开放2个大餐厅和1个小餐厅,可供500名学生就餐. (1)求1个大餐厅和1个小餐厅分别可供多少名学生就餐? (2)若5个餐厅同时开放,请估计一下能否供应全校的750名学生就餐?请说明理由.
解: (1)设1个大餐厅和1个小餐厅分别可供x名,y名学生就餐,
x+2y=400
2x+y=500
解得:
x=200
y=100
(2) 5个餐厅同时开放: 3×200+2×100=800
答: (1) 1个大餐厅和1个小餐厅分别可供400名,100名学生就餐. (2)若5个餐厅同时开放,能供应全校的750名学生就餐.
∵800>750
∴能供应全校的750名学生就餐.
列方程组解应用题的一般步骤:
(1)设:设未知数
(2)列:根据相等关系列出方程组;
(3)解:解所列方程组,得出未知数的值;
(4)验:检验所求未知数的值是否正确, 是否符合实际意义;
(5)答:写出答案.
1、课本101页 习题8.3 第 2、 5题
2、选做:课本101页 习题8.3 第8题
二元一次方程组的解法:
根据方程未知数的系数特征确定用哪一种解法.
基本思想或思路——
常用方法——
温顾而知新:
消元
代入消元法
加减消元法
8.3实际问题与二元一次方程组(1)
小街镇一中
王佳鹏
设问3:等量关系是什么呢?
设问1:本题需要大家解决什么问题呢?
设问2:你有什么办法?
先根据问题中给定的数量关系求出每头大牛和每头小牛1天各约需用饲料量,再来判断估计是否正确
(1)1天30头大牛所用的饲料+15头小牛的所用的饲料=675Kg
(2)1天42头大牛所用的饲料+20头小牛的所用的饲料=940Kg
判断李大叔的估计是否正确 ?
养牛场原有30头大牛和15头小牛,1天约用饲料675kg.一周后又购进12头大牛和5头小牛,这时1天约用饲料940kg.饲养员李大叔估计每头大牛1天约需饲料18~20kg,每头小牛1天约需饲料7~8kg,你能通过计算检验他的估计吗?
共675kg
大牛
小牛
30头
15头
xkg
ykg
30x
15y
+
共940kg
大牛
小牛
(30+12)头
(15+5 )头
xkg
ykg
(30+12)x
(15+5)y
+
解:设平均每头大牛和每头小牛1天各约需饲料x kg和y kg.
这就是说,每头大牛约需饲料20kg,每头小牛约需饲料5kg.因此,饲料员李大叔对大牛的食量估计较准确,对小牛的食量估计偏高
解得:
20
5
化简得:
①
②
解:设平均每头大牛和每头小牛1天各约需饲料xkg和ykg.
共675kg
大牛
小牛
30头
15头
xkg
ykg
30x
15y
+
共940kg
大牛
小牛
(30+12)头
(15+5 )头
xkg
ykg
12x + 5y
解:设平均每头大牛和每头小牛1天各约需饲料x kg和y kg.
共940-675=265kg
12
5
(30+12)x+(15+5)y
化简得:
列方程组解应用题的一般步骤:
(1)设:设未知数
(2)列:根据相等关系列出方程组;
(3)解:解所列方程组,得出未知数的值;
(4)验:检验所求未知数的值是否正确, 是否符合实际意义;
(5)答:写出答案.
某家商店的账目记录显示,某天卖出9支牙刷和6盒牙膏,收入60元;另一天,以同样的价格卖出同样的15支牙刷和10盒牙膏,收入90元。这个记录是否有误?如果有误,请说明理由。
共60元
牙刷
牙膏
9
6
x
y
9x
6y
+
共90元
牙刷
牙膏
15
10
x
y
15x
10y
+
解:设1支牙刷x元,1盒牙膏y元,
解: (1)设1支牙刷x元,1盒牙膏y元,
9x+6y=60
15x+10y=90
化简得:
3x+2y=20
3x+2y=18
此方程组无解,说明记录有误
答:这个记录有误。
①
②
某校共有3个大餐厅和2个小餐厅,经过测试:同时开放1个大餐厅和2个小餐厅,可供400名学生就餐;同时开放2个大餐厅和1个小餐厅,可供500名学生就餐. (1)求1个大餐厅和1个小餐厅分别可供多少名学生就餐? (2)若5个餐厅同时开放,请估计一下能否供应全校的750名学生就餐?请说明理由.
解: (1)设1个大餐厅和1个小餐厅分别可供x名,y名学生就餐,
x+2y=400
2x+y=500
解得:
x=200
y=100
(2) 5个餐厅同时开放: 3×200+2×100=800
答: (1) 1个大餐厅和1个小餐厅分别可供400名,100名学生就餐. (2)若5个餐厅同时开放,能供应全校的750名学生就餐.
∵800>750
∴能供应全校的750名学生就餐.
列方程组解应用题的一般步骤:
(1)设:设未知数
(2)列:根据相等关系列出方程组;
(3)解:解所列方程组,得出未知数的值;
(4)验:检验所求未知数的值是否正确, 是否符合实际意义;
(5)答:写出答案.
1、课本101页 习题8.3 第 2、 5题
2、选做:课本101页 习题8.3 第8题
